Because of its excellent performance and compatibility with conventional Si CMOS processing, SiGe HBT technology has recently received a great deal of attention in radio frequency (RF), microwave and extreme environment applications.^[1,2] Since the existence of bandgap-engineering in the base region, the narrowed-bandgap induced by the Ge profile retards the classical problems associated with cooling conventional transistors, such as base freezeout, carrier diffusivity and mobility degradation.^[3–5] As a consequence, nearly all the transistor metrics improve with temperature decreasing, which enables SiGe HBT to operate well in a low temperature range. Obviously, on the other hand, SiGe HBTs also suffer some degradations in AC and DC characteristics as temperature increases.^[3,6,7] However, it is lucky to find that the speed of such a degradation is not very fast. For example, even at 300 °C IBM the 2nd generation SiGe HBT also possesses a current gain of above 100 and f_T above 75 GHz.^[8] It demonstrates a potential of SiGe HBT operating over a wide range of temperature. Therefore, it is vital to investigate the physics of SiGe HBT model parameters over a wide temperature, and also important to build the temperature dependences of model parameters with good fidelity.

A completed transistor model generally includes two parts: the small-signal model and the large-signal model.^[9] The small-signal model is a linear approximation of the large-signal model in a given bias condition and can accurately describe the transistor characteristics. The extraction of small-signal model parameters is less complicated, and it is promising to obtain the large-signal model parameters. Therefore, the temperature dependences of model parameters related to the small-signal equivalent circuit are presented in this work. The small-signal electrical elements in the SiGe HBT HICUM model in off-state are first extracted at a given temperature, and the corresponding temperature coefficients for each model parameter are then obtained based on the proposed temperature formulas. This paper provides a theoretical guide for designing the device and circuit of SiGe HBTs working in a wide temperature range.

After the bias-independent extrinsic parasitic elements are removed through a standard ‘open’ and ‘short’ de-embedding pattern, the small-signal equivalent circuit of the SiGe HBT HICUM model under cut-off mode is obtained, as shown in Fig. 1.^[10] The temperature dependences of resistance and capacitance originate from the physical quantities such as the intrinsic carrier density, diffusivity or mobility. The temperature coefficients related to the model parameters in Fig. 1 are respectively the effective bandgap voltages V_gEeff, V_gCeff, and V_gSeff, temperature exponents ζ_RB for base resistance, ζ_RCX for collector resistance, ζ_RSU for substrate resistance, and ζ_RE for emitter resistance.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Simplified small-signal equivalent circuit in SiGe HBT HICUM model biased at off-state.

The devices under test are vertical NPN SiGe HBTs and five temperature points 218 K, 248 K, 298 K, 373 K, and 473 K are adopted. DC characteristics including the forward-Gummel and R_C_flyback are measured with an Agilent B1500 Semiconductor Parameter Analyzer, and the S-parameter measurements are carried out in a microwave probing system using a vector network analyzer over a frequency range of 100 MHz–25 GHz.

The junction capacitances are first extracted from the cold S-parameters measurement.^[11] For the BE junction capacitance C_be and BC junction capacitance C_bc, base voltage V_B is swept from −1 V to 0.4 V under a fixed V_C = 0 V. Similarly, for the CS junction capacitance C_jS, V_C is swept from −0.4 V to 1.5 V with a constant V_B = V_S = 0 V. Then the junction capacitance can be directly determined from the following non-linear rational function fitting over the whole frequency range:^[11]

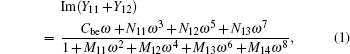
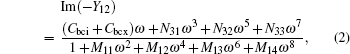
The coefficients N_{i j} and M_{i j} of other high-order terms each are a function of the circuit elements in Fig. 1. Figure 2 shows the variations of Im(Y₁₁ + Y₁₂), Im(−Y₁₂), and Im(Y₂₂ + Y₁₂) with angular frequency ω for 1 × 0.2 × 16 μm² SiGe HBT biased at V_B = V_C = 0 V at room temperature. Excellent agreement is found over the whole frequency range, and the junction capacitances are respectively obtained to be 55.64 fF (55.04 fF, 56.24 fF) for C_be, 62.78 fF (61.95 fF, 63.21 fF) for C_bcx + C_bci, and 26.10 fF (25.92 fF, 26.28 fF) for C_ts. Confidence intervals (included in the above brackets) are narrow and hence the extracted junction capacitances are credibly accurate. For each operation point and measurement temperature, an appropriate fitting frequency range is adopted to obtain the global junction capacitance. As a consequence, the bias-dependent junction capacitances at different temperatures are determined, then the junction capacitance model parameters, zero-biased depletion capacitances, grading coefficients, and built-in voltage are obtained, which will be discussed in the following section.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Comparison between the measured (symbols) and fitting results (solid lines) of formulas (1)–(3) for 1 × 0.2 × 16 μm2 SiGe HBT biased at VB = VC = 0 V at room temperature.

The substrate resistance R_SU can be extracted by using the reported cold S-parameter approach.^[12] The external collector resistance R_CX can be determined through the convenient flyback method.^[13] As for the emitter resistance R_E, a novel extraction method has been proposed based on forward-Gummel measurements in our pervious study.^[14] In the medium current region we can obtain

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Typical fitting result of Eq. (4) for a 1 × 0.2 × 16 μm2 SiGe HBT.

As in our pervious study, the remaining model parameter R_B can be obtained based on the nonlinear rational function fitting.^[15] Taking a 4 × 1.2 × 20 μm² SiGe HBT under off-states for example, as shown in Fig. 4, R_B and R_CX both decrease with the external BC junction C_bcx increasing. R_B is confined within a narrow range from 9.88 Ω to 10.59 Ω when R_CX drops to zero. Then with the aid of pre-determined R_CX of 4.18 Ω (already extracted from R_C_flyback method), R_B is obtained to be 10.17 Ω. In other words, the base resistance here is directly extracted from cold S-parameters without making any numerical optimization.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Plots of RB and RCX versus Cbcx for 4 × 1.2 × 20 μm2 SiGe HBT in cut-off state.

Through the given method as discussed above, the series resistances R_CX, R_SU, R_E, and R_B at each temperature can be extracted and the plots will be given below. By far, the problem of extracting each electrical element in the small-signal equivalent-circuit as shown in Fig. 1 has been completed. Then based on these extracted results at each temperature, the temperature dependence can be established, which will be discussed in the following section.

In the HICUM model, the temperature dependence of model parameters is described via the physical quantities such as intrinsic carrier density, diffusivity or mobility. The temperature dependence of internal base resistance R_B here depends on the carrier mobility in the neutral region. Then zero-bias resistance is described as:^[16]

As in Ref. [11], all junction depletion capacitances are modeled in terms of the capacitance at zero bias C_j0, a built-in voltage V_D and a grading coefficient z_j. In HICUM the grading coefficient z_j is assumed to be a constant and temperature-independent. To access the temperature dependence of built-in voltage V_D, an auxiliary voltage V_Dj(T₀) at given reference temperature T₀ is calculated as indicated in Ref. [16] and given as follows:

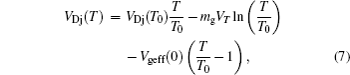
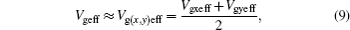
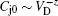
The grading coefficient z here does not depend on temperature. As reported in Ref. [11], the well-known junction depletion capacitances can be modeled, respectively, as

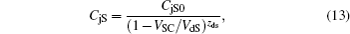
It is noted that the built-in voltage V_D is temperature dependent and the grading coefficient Z_d is temperature-independent in the HICUM model, therefore, V_D cannot be set as a constant similar to the case at room temperature. A novel parameter extraction flow for the depletion capacitances is recommend. First, the C–V characteristics at given reference temperature T₀ is fitted directly, then the built-in voltage V_D, zero-biased capacitance C_j0 and grading coefficient Z_d will be obtained simultaneously if high accuracy exists. Otherwise, set V_D as the default value, and extract the C_j0 and Z_d from the C–V curve fitting. Finally, the values of V_D and C_j0 at different temperatures can be determined from the corresponding C–V curve fitting under the assumption of Z_d(T) = Z_d(T₀). Thus, the temperature dependences of V_D(T) and C_j0(T) are obtained.

In HICUM the temperature dependence of model parameters is assumed to be irrelevant to device size, therefore, the extraction of temperature dependence for a single transistor geometry can also be applied to other-sized devices. The results for a 1 × 0.2 × 16 μm² SiGe HBT are presented in this work. According to Eqs. (6)–(13), the obtained relative temperature coefficients are shown in Table 1. The variations of built-in voltage V_D and zero-biased depletion capacitances C_j0 for BE junction, BC junction, and CS junction, with temperature are shown in Figs. 5–7, respectively. Excellent agreement is obtained between the extracted and fitted model parameters at most temperature points.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Temperature dependences of zero-bias capacitance and built-in voltage for BE junction.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Temperature dependences of zero-bias capacitance and built-in voltage for BC junction.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Temperature dependences of zero-bias capacitance and built-in voltage for CS junction.

Table 1.

Table 1.

Table 1. Extracted temperature coefficients for 1 × 0.2 × 16 μm2 SiGe HBT. . Zdei VgEeff/V Zdci VgCeff/V Zdsi VgSeff/V 0.184 0.949 0.2715 0.9174 0.06075 0.8136 mg ζRB ζRE ζRCX ζRSU 3 0.6283 −0.3456 0.7533 0.6049

Table 1. Extracted temperature coefficients for 1 × 0.2 × 16 μm2 SiGe HBT. .

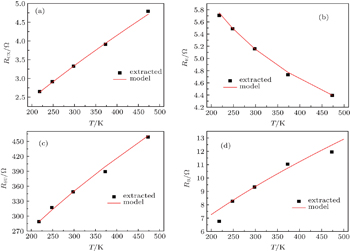
The temperature dependences of series resistances (R_B, R_CX, R_E, and R_SU) are shown in Fig. 8, from which good agreement is obtained over the whole measurement temperature range from 218 K to 473 K. Besides, it is found that the variation tendency of R_E is different from those of the other three resistances as temperature increases. R_B, R_CX, and R_SU gradually increase while R_E decreases with temperature increasing, which may be due to the different scattering mechanisms contributing to carrier mobility.^[9]

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Temperature dependences of series resistances of (a) RCX, (b) RE, (c) RSU, and (d) RB.

Because of the low doping concentration, the carrier mobilities in base, collector and substrate region are mainly dominated by the lattice vibration scattering, which shows a temperature dependence of T^3/2 and increases with temperature increasing. Therefore, the carrier mobility in these regions decreases and the corresponding series resistances increase as temperature increases. While in the emitter region, it is the ionized impurity scattering that dominates the carrier mobility due to the higher doping concentration (generally at a level of 10²⁰ cm⁻³). The ionized impurity scattering shows a temperature dependence of T^3/2 and hence decreases with temperature increasing; as a result, the carrier mobility in the emitter region increases and then the emitter resistance R_E decreases.

In this paper, the temperature dependences of small-signal model parameters for SiGe HBT HICUM under cut-off mode are presented from 218 K to 473 K. The depletion capacitances are extracted from the cold S-parameter measurements. Emitter resistance R_E is obtained from the forward-Gummel measurement. Base resistance R_B is gained from cold S-parameters based on the rational function fitting. Then the temperature dependences of model parameters are determined based on the established temperature formulas. The proposed method is verified with a 1 × 0.2 × 16 μm² SiGe HBT and good agreement is obtained over the whole temperature range. These results provide a theoretical guide for designing devices and circuits of SiGe HBTs in a wide temperature range.