Tunnel Field-Effect Transistors (TFETs) are a new concept of device that has been proposed as a promising option to conventional MOSFET. Owing to different operating principles, the TFETs have attracted much attention because of their steep subthreshold swing (SS < 60 mV/dec).^[1–4] One significant task for TFETs is to study which factors deteriorate sub-threshold characteristics. However, in many papers just the effects of the trap density on subthreshold swing (SS) and off-state current (I_off) were studied, and interface traps (ITs) and phonon scattering were considered for TFET by a few authors.^[5–9] Furthermore, there are few reports of physically detailed effect of gate leakage current on TFET.

In general, the tunneling happens uniformly along the gate on the source side, and high-κ gate insulator as well as lattice mismatch in source-channel junction could induce those traps existing at the interface. Such an important issue is that the influences of trap level and phonon-assisted tunneling on the DG-TFET need further physical insight. In this paper, we focus on the TAT and gate leakage current behavior in DG-TFET. It is shown that different positions of trap and phonon scattering can result in the degradations of the SS and TAT current.

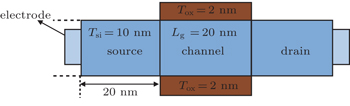
In this paper, the device structure under investigation is an all Si double-gate n-TFET (DG-nTFET), as illustrated in Fig. 1. Figure 1 shows the modeled device geometry with high-κ (t_ox = 2 nm, κ = 21) double-gate structure. The gated channel length (L_g) is 20-nm doped source region length and doped drain region length are both 20 nm. It consists of a thin (T_Si = 10 nm) intrinsic source (n-type, 10¹⁵ cm⁻³), p-type source (10²⁰ cm⁻³), and n-type drain (10²⁰ cm⁻³). The metal gate work function used is 4.1 eV. For simplicity, abrupt doping profiles are used, and we assume semiconductor/oxide interface and source/channel interface where ITs are most likely located.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Device structure of a DG n-type TFET.

To elucidate the relationship between TAT current and phonon scattering, and that between gate leakage current and tunneling in DG-nTFET, the device simulation setup includes the dynamical nonlocal-path band-to-band tunneling (BTBT) model, dynamic nonlocal path trap-assisted tunneling, enhanced Lombardi model with high-κ degradation, a fully quantum-mechanical gate leakage current tunneling model, and hot-carrier injection model. When oxide is thinner than 3 nm, the gate leakage and mobility degradation must be considered. In the TAT simulations, a constant tunneling mass (m_e = 0.19m₀, m_h = 0.2m₀) is used, and nonlocal BTBT model (A = 4×10¹⁴ cm⁻³·s⁻¹, B = 2×10⁷ V·cm⁻¹) is also adopted. Carrier bulk lifetime and trap capture cross section are 0.1 μs and 10⁻¹⁰ cm² respectively. In addition, carrier injection model calculates the hot-carrier injection current by using the nonequilibrium energy distribution which contributes to distinguishing the influences of two different mechanisms on gate leakage current. Even more importantly, the influences of optical phonon (OP) assisted inelastic tunneling and acoustic phonon (AP) scattering on the carrier mobility could be effectively studied. In all DG-nTFET simulations in this paper we assume V_DS = 0.5 V.

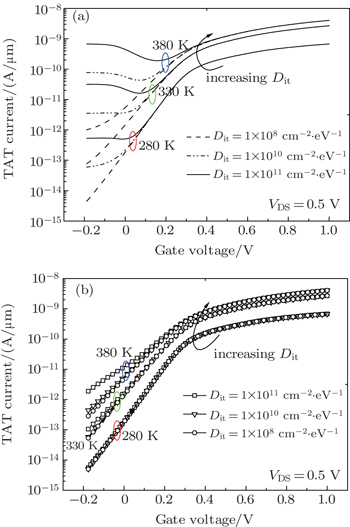
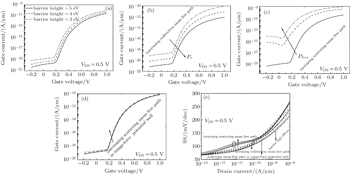
The simulated TAT currents in this work are plotted in Fig. 2, in which traps are located at different interfaces. Figure 2(a) shows the measured TAT currents at the gate/channel interface for temperatures ranging from 280 K to 380 K. For V_DS = 0.5 V, TAT current deteriorates by increasing D_it, owing to more traps that introduce greater trap-assisted tunneling numbers. However, when those traps are located at the source/channel interface for different temperatures, trap-assisted tunneling through trap (location see Fig. 1) is located at source/channel interface unlike TAT though gate/channel interface traps. Temperature influence is suppressed and it cannot further increase TAT current. It can be indicated that trap-assisted tunneling mainly takes place in channel surface rather than through bulk. The temperature dependence of this trap-assisted tunneling dominated leakage current rises with the increasing of temperature as expected. For V_GS values ranging from −0.2 V to 0.2 V, TAT current is mainly due to trap-assisted tunneling, and the recombination rate is proportional to exp[−(E_F,n−E_C)/κT].^[10] Hence, TAT current can be effectively suppressed at low temperatures.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. TAT characteristics of the DG-nTFET, showing variable interface trap density Dit with uniquely different temperature dependences in a range of 280 K–380 K. (a) Influence of trap location (gate/channel) on the TAT characteristic. (b) Influence of trap location (source/channel) on the TAT characteristic.

To obtain further insight, we study the influence of trap levels on TAT characteristics of DG-nTFET with D_it = 10¹⁰ cm⁻²·eV⁻¹. When trap level turns closer to valence band at the gate/channel interface in source region, the simulation results display that TAT current would increase as shown in Fig. 3(a). In practice, that the same energy phonons contribute to TAT transitions is limited at different levels. With the increasing of energy level of trap, the capture ability of trap is weakened. Carriers will not possess enough energy to arrive at the interface traps, and finally, they reach the source region again. The reason for such a characteristic of TAT can be explained, owing to phonon absorption-assisted transport as exemplified in Fig. 3(d). Figure 3(d) clearly shows carriers tunneling from source region into trap states (dotted circle) and its subsequent thermal emission into the conduction band in channel. With increasing trap energy level, none of all electrons can arrive at a higher level and they cannot be efficiently scattered. TAT current decreases with the increase of trap level.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Influences of the trap energy level on the TAT current through gate/channel interface trap. (a) The TAT current increases with increasing proximity of the trap level to the source valence band. (b) Off-state and TAT current increase with increasing the scattering phonon energy. (c) The TAT current is lowest when trap level is far away from the valence band with BTBT and TAT. (d) Energy-position of one-dimensional DG-nTFET with phonon-assisted scattering. It can be clearly seen that phonon absorption assisted transport occurs at the gate/channel interface.

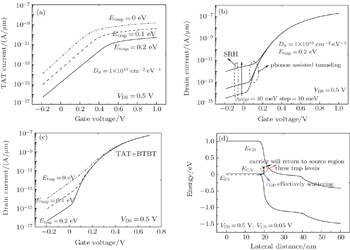
Here, a close match with experimental data is obtained when considering BTBT component and TAT component^[12] as shown in Fig. 3(c). This indicates that TAT is dominant and degrades the swing at low gate voltages. Figure 3(b) shows that off-state current and SS increase with the increase of effective optical phonon energy as expected. Shockley–Read–Hall Recombination (SRH) and TAT rate increase at large scattering rate. Optical-phonon scattering rate is

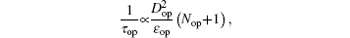
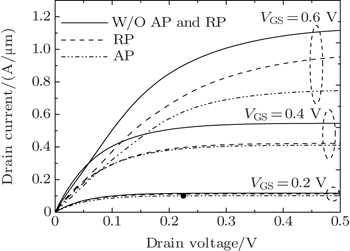
When the gate voltage is over threshold voltage, the remote phonons (RPs) scattering and acoustic phonons (APs) scattering begin to have an influence, which stem from the high-κ dielectrics. Carriers are scattered into trap level, followed by thermal emission into the conduction band. An increase in V_DS results in reducing the electron concentration in the channel, and the electrons are now pulled back to the end of the drain. The mobility would suffer RP scattering. Figure 4 shows the simulated output characteristics for different values of V_GS in the cases with and without (W/O) scattering. Elastic scattering due to acoustic phonon and remote phonon comes into effect at larger gate biases. As can be seen, the on-state current is obviously reduced by scattering because of acoustic phonon and remote phonon. First, the remote phonon scattering can affect the electron mobility, resulting in the significant decrease of drift-diffusion current. On the other hand, the acoustic phonon scattering can reduce the BTBT generation rate at the source/channel injunction, since part of the electrons entering into the drain are backscattered.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. IDS–VDS characteristics for the DG-nTFET at VGS = 0.2 V, 0.4 V, and 0.6 V in the cases with and without scattering. Source/channel interface scattering (AP) and electron mobility scattering (RP) are considered independently. These elastic scatterings would reduce BTBT rate and the mobility.

In many cases, there are few researchers to discuss the gate leakage current. On-state current can be effectively and easily improved by using a thinner high-κ gate dielectric. However, this method has a major disadvantage, that is, the gate leakage current. The leakage floor would reduce device reliability. For DG-nTFET, the leakage floor can be divided into hot-carrier injection current and direct tunneling current. Direct tunneling and hot-carrier injection are the main gate leakage mechanism for oxides thinner than 3 nm. With the decrease of the device size, hot carrier effect failure has received much attention nowadays, it becomes one of the main failure mechanisms, especially in TFET.

A comparison of the apparent shift in the onset of gate leakage among different V_DS values is shown in Fig. 5. The increase of apparent shift in the voltage of the smallest leakage floor can be clearly seen when V_DS increases linearly. When V_GS is smaller than V_DS, carriers indirectly tunnel into the channel, followed by drift-diffusion into drain. Direct tunneling becomes limited by the indirect tunneling. Once V_GS is over V_DS, the gate direct tunneling current increases exponentially. Direct current density is:^[14]

Fig. 5.

	Figure Option ViewDownloadNew Window
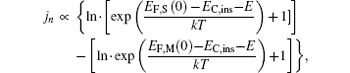
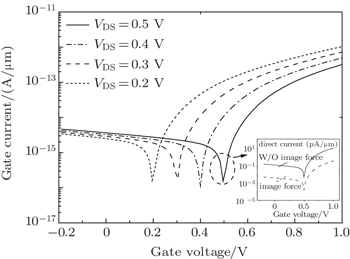	Fig. 5. Gate leakage characteristics for different values of the drain voltage. The inset shows the image force can reduce the leakage floor by two orders of magnitude.

When the gate oxide thickness reduces to 2 nm, oxide barriers are easily affected by the image force. The image force can reduce the tunneling barrier, hence, the gate direct tunneling current decreases as shown in the inset of Fig. 5.

Figure 6 shows a hot-carrier injection current obtained from the simulations of three different types of scattering free paths and barrier heights. Figure 6(a) presents the plots of gate current versus gate voltage for different heights of the Si–H_fO₂ barrier for the DG-nTFET. Unless otherwise mentioned, the device dimensions and parameters are both kept unchanged for our simulations. The barrier height is a function of insulator field, and the insulator field can directly affect electron distribution function. The injection probability of hot-carrier into gate insulation would reduce due to higher barrier height. The probability can be written as^[13]

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. Gate leakage characteristics of the DG-nTFET, showing (a) barrier height dependence: higher barrier can effectively reduce the hot-carrier injection current; (b) redirection mean free path dependence: leakage floor can be limited by longer redirection distance; (c) scattering mean free path in semiconductor: the scattering rate of hot-carrier would be increased by increasing the scattering path; (d) scattering length dependence in the image-force potential well: this effect is similar to electron traveling a distance in semiconductor, but it is not obvious; (e) SS versus drain current for different free paths, barrier heights and image-forces.

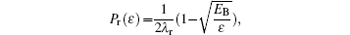
In addition, the gate leakage current is also influenced by scattering mean free path λ in semiconductor. The probability is given by the following expression:^[13]

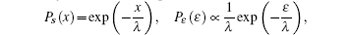
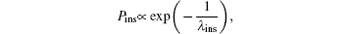
In this paper, we present the TAT current and gate leakage current characteristics of all-Si DG-nTFET. Based on different defect levels, phonon energies and trap densities, transfer characteristics of subthreshold which suffers the influence of phonon scattering are studied. The phonon with higher scattering energy and the phonon closer to the valence band would deteriorate SS and off-state current. The DG-nTFET leakage floor is vulnerable to not only barrier height of semiconductor/oxide, but also scattering mean free path. Leakage floor can be improved by increasing the barrier height and a robust surface processing.