† These authors contributed equally.
‡ Corresponding author. E-mail:
Project supported by the Recruitment Program of Global Youth Experts of China, the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA09010401), the Science and Technology Development Program of Jilin Province, China (Grant No. 20150623002TC), and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20131139).
Although significant progress has been made in many aspects of the emerging aprotic Li-O 2 battery system, an in-depth understanding of the oxygen reactions is still underway. The oxygen reactions occurring in the positive electrode distinguish Li-O 2 batteries from the conventional Li-ion cells and play a crucial role in the Li-O 2 cell’s performance (capacity, rate capability, and cycle life). Recent advances in fundamental studies of oxygen reactions in aprotic Li-O 2 batteries are reviewed, including the reaction route, kinetics, morphological evolution of Li 2 O 2 , and charge transport within Li 2 O 2 . Prospects are also provided for future fundamental investigations of Li-O 2 chemistry.
Aprotic Li-O 2 batteries have much greater gravimetric energy density than the traditional Li-ion technologies, making them promising candidates for future energy storage systems. [ 1 – 9 ] The aprotic Li-O 2 battery, initially introduced by Abraham et al ., [ 10 ] is typically composed of a Li metal anode, an aprotic Li + electrolyte, and an air cathode, in which the active material (O 2 ) of the cathode is drawn from the atmosphere. Currently, the aprotic Li-O 2 battery development encounters substantial scientific and technological challenges that impede its practical applications including high charging over-potential (which limits round-trip efficiency), [ 11 , 12 ] poor stability of cathodes and electrolytes (which decreases cycle life), [ 13 – 15 ] deposition of insulating Li 2 O 2 product (which degrades the cell’s capacity), [ 16 , 17 ] and safety issues associated with Li metal anodes. [ 18 , 19 ] Most of these challenges are related to the oxygen reactions occurring in the positive electrodes of the aprotic Li-O 2 cells. Therefore, to tackle these issues effectively, an in-depth understanding of the oxygen reaction mechanisms is crucial. In this review, we summarize a few fundamental aspects of the oxygen electrode reactions in aprotic Li-O 2 batteries, including the reaction route, kinetics, morphological evolution of Li 2 O 2 and charge transport within Li 2 O 2 .
Without considering any of the possible parasitic side reactions, the fundamental chemistry of an aprotic Li-O 2 battery during discharge undergoes these possible elementary reactions: [ 20 – 24 ]

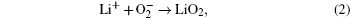
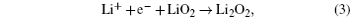
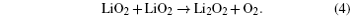
To identify the ORR mechanisms in aprotic Li-O 2 cells, several research groups investigated the ORRs with multiple techniques including voltammetry, [ 20 – 23 ] electrochemical surface-enhanced Raman spectroscopy (EC-SERS), [ 24 – 26 ] differential electrochemical mass spectrometry (DEMS), [ 27 ] etc. For instance, Laoire et al . studied ORRs in various organic solvents (such as acetonitrile [ACN] and dimethylsulfoxide [DMSO]) containing various cations (such as tetrabutylammonium [TBA + ] and alkali metal ions of Li + , Na + , and K + ) using cyclic voltammetry. [ 20 , 21 ] Meanwhile, the reaction between 
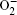

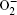
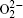
 | Fig. 1. Cyclic voltammetry at a roughened Au electrode in O 2 saturated 0.1 MnBu 4 NClO 4 in CH 3 CN containing various concentrations of LiClO 4 as indicated. The scan rate was 1 V·s –1 . [ 24 ] |
The proposed ORR mechanisms (Eqs. (
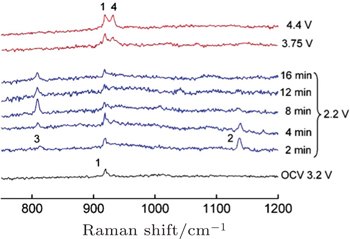 | Fig. 2. In situ SERS during O 2 reduction and re-oxidation on Au in O 2 -saturated 0.1 M LiClO 4 –CH 3 CN. Spectra collected at a series of times and at the reducing potential of 2.2 V versus Li/Li + followed by other spectra at the oxidation potentials shown. The peaks are assigned as follows: 1) C–C stretch of CH 3 CN at 918 cm –1 , 2) O–O stretch of LiO 2 at 1137 cm –1 , 3) O–O stretch of Li 2 O 2 at 808 cm –1 , and 4) Cl–O stretch of 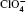 |
In addition, McCloskey et al . employed cyclic voltammetry (CV) and differential electrochemical mass spectrometry (DEMS) to study the oxygen reactions in aprotic Li-O 2 cells with a lithium bis(trifluoromethanesulfonyl)imide(LiTFSI)-dimethoxyethane (DME) electrolyte. [ 27 ] Interestingly, only one peak for ORRs was observed (Fig.
 | Fig. 3. (a) CVs showing O 2 reduction and re-oxidation in 0.5 M NBu 4 TFSI (green, right ordinate) and 1 M LiTFSI (blue, left ordinate). (b) Linear sweep voltammetry at 0.5 mV/s using the DEMS cell (XC 72 carbon cathode, 1 M LiTFSI in DME). The solid line is the current, and the points are O 2 (and CO 2 ) measured by the DEMS. e – /O 2 was determined by comparing the current to the moles of O 2 consumed or evolved. [ 27 ] |
Early CV studies of ORRs in aprotic solvents reported by Laoire et al . are excellent, but the reaction products and intermediates cannot be identified with certainty by these conventional electrochemical methods; [ 28 ] therefore, the mechanisms that were proposed based on CV measurements are questionable. The extra peaks of ORRs in CVs may be due to the existence of H 2 O in the electrolyte, as suggested by a recent work, [ 29 ] and the effects of residual H 2 O (or any proton sources) need further clarification. By EC-SERS, the ORR intermediate LiO 2 has been detected directly, which is very beneficial for the formulation of the ORR mechanisms. Spectroscopy-based techniques will continue to play a key role in better understanding the ORRs in various aprotic Li-O 2 batteries that incorporate a broad range of aprotic electrolyte solvents. However, DEMS experiments demonstrate that an overall two-electron process is obtained within the time resolution (seconds) of this technique, which means that LiO 2 may not be a stable intermediate and could rapidly transform to Li 2 O 2 . This contradiction between the DEMS and SERS results needs further study. So far, there is no consensus on the path of LiO 2 transformation to Li 2 O 2 under the conditions of Li-O 2 cell operation, i.e., whether it is dominated by electrochemical reduction or chemical disproportionation. Further investigations are urged, seeking a better understanding of ORRs in aprotic Li-O 2 batteries.
Understanding the intrinsic ORR kinetics and transport limitations associated with Li 2 O 2 formation is crucial to the development of aprotic Li-O 2 batteries with the desired rate capabilities. To explore ORR kinetics, Gallant et al . investigated the ORR over-potentials on a carbon nanotube-based cathode by using galvanostatic and potentiostatic intermittent titration (PITT) techniques. [ 30 ] Under potentiostatic conditions, the average current increases in magnitude as the voltage is reduced from 2.76 V to 2.0 V (Fig.
 | Fig. 4. (a) Current vs. capacity of CNT electrodes discharged potentiostatically over a range of potentials between 2.0 V and 2.76 V. (b) PITT discharge of CNT electrodes from an open circuit (∼ 3.15 V) with a voltage step of 5 mV and a current cutoff per step of 1 mA/g C . Inset: zoom-in of the PITT response in the capacity range below 1 mA·h/g C , where the current corresponds to only capacitive discharge. (c) Voltage vs. capacity of CNT electrodes discharged galvanostatically between 10 mA/g C and 1000 mA/g C . (d) Tafel plot of voltage vs. carbon true surface area-normalized current for electrodes discharged potentiostatically (blue circles) from (a) and galvanostatically (gray circles) from (c). [ 30 ] |
Many studies of discharge behavior and kinetic process using typical Swagelok-type cells with carbon cathodes were reported in the literatures, [ 30 , 31 ] however, Viswanathan et al . argued that these results may fully mask the fundamental kinetic behavior due to the cell’s intrinsic impedance. It is critical to eliminate the cell iR drop for measuring the fundamental kinetic over-potential. Therefore, Viswanathan and associates estimated the kinetic over-potentials by using a bulk electrolysis cell with a flat, polished, small-surface glassy carbon (GC) electrode. [ 32 ] Figure
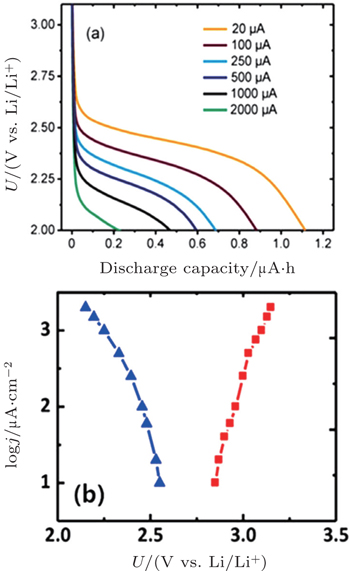 | Fig. 5. (a) Output potential during Li-O 2 galvanostatic discharge in the bulk electrolysis cell at the current densities given in the legend. (b) Experimental Tafel plots for Li-O 2 discharge (ORR, blue triangles) and for charging following discharge (OER, red squares). [ 32 ] |
The reported morphology of Li 2 O 2 formed on a cathode is also controversial. Viswannathan et al . reported homogeneous films of Li 2 O 2 deposited on a small-surface GC cathode in an electrolysis cell, observed by atomic force microscopy (AFM). [ 33 ] Adams et al . also observed the formation of a quasi-amorphous peroxide film at high current rates, as shown in Figs.
 | Fig. 6. FESEM images at a magnification of 20000 of (a) the pristine cathode and after full discharge at (b) 5 mA/cm 2 , (c) 10 mA/cm 2 , (d) 25 mA/cm 2 , (e) 50 mA/cm 2 , and (f) 100 mA/cm 2 , with the corresponding discharge curves shown as insets. Scale bar = 400 nm. [ 16 ] |
Other researchers also reported that the toroid-like Li 2 O 2 particles are formed on various types of carbon cathodes, especially at low discharge current density. [ 30 , 34 , 35 ] For instance, Shao-Horn and colleagues revealed the morphology evolution of these toroid-like products by using transmission electron microscopy (TEM), the formation originally began with the nucleation of small particles on the side wall of CNT and evolved upon continued discharge. The TEM investigation also showed that these toroids are highly crystalline with the Li 2 O 2 (0001) facet normal to the axis of the toroid as shown in Fig.
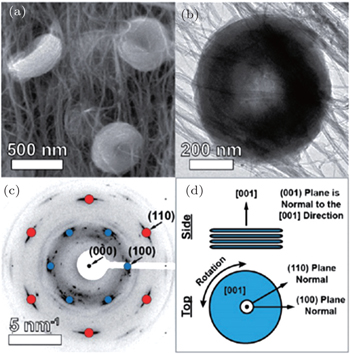 | Fig. 7. Electron diffraction investigation of individual Li 2 O 2 particles. (a) SEM and (b) bright-field TEM images of toroid particles. (c) Simulated Li 2 O 2 [001] zone axis superimposed over an experimental diffraction pattern for the particle pictured in panel (b). (d) Side-view and top-view schematics of a stack of crystallite plates. [ 34 ] |
Understanding the Li 2 O 2 oxidation reactions is also crucial to the development of Li-O 2 cells with high energy efficiency and long cycle life. However, the Li 2 O 2 decomposition reactions at the cathode are complex and have not been fully understood so far. As for ORRs, the following mechanisms for Li 2 O 2 oxidation reactions have been proposed: [ 24 , 30 , 31 , 36 – 38 ]

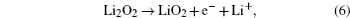
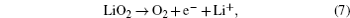

The electrochemical decomposition of Li 2 O 2 to Li + and O 2 (Eq. (
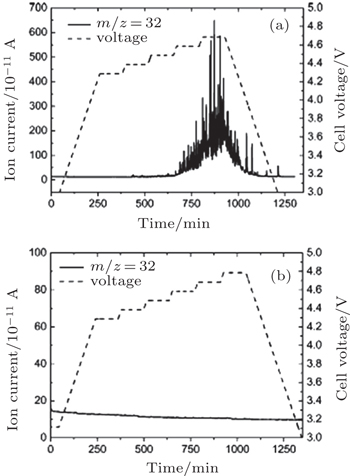 | Fig. 8. Variation of ion current corresponding to O 2 evolution as a function of time. The voltage was increased by 100 mV every 120 min. (a) Electrode with Li 2 O 2 and (b) electrode without Li 2 O 2 . [ 36 ] |
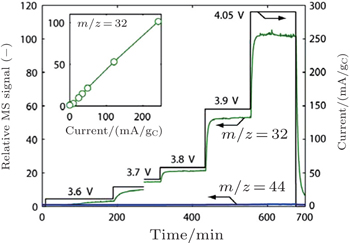 | Fig. 9. Differential electrochemical mass spectrometry on oxidation of Li 2 O 2 , signal for m / z = 32 (O 2 ) and m / z = 44 (CO 2 ) in response to stepwise increase in oxidation current. Inset: m / z = 32 signal as a function of oxidation current, showing proportional relationship. [ 24 ] |
However, Lu and Shao-Horn [ 31 ] speculated that the rising potential in the oxidation process is due to different mechanisms for OER (Fig.
 | Fig. 10. Proposed reaction mechanism of Li-O 2 recharge. The OER process associated with stage I (sloping and catalyst-insensitive) is attributed to a de-intercalation process via a solid-solution route from the outer part of Li 2 O 2 to form LiO 2 -like species on the surface (Li 2 O 2 → LiO 2 + Li + + e – ), where LiO 2 -like species disproportionate to evolve O 2 (LiO 2 + LiO 2 → Li 2 O 2 + O 2 ), yielding an overall 2e – /O 2 OER process (Li 2 O 2 → 2Li + + O 2 + 2e – ). The OER process at the flat potential plateau (stage II) is attributed to the oxidation of bulk Li 2 O 2 particles to form Li + ions and O 2 (Li 2 O 2 → 2Li + + 2e – + O 2 ) via a two-phase transition. Lastly, a rising charge plateau after stage II has been assigned to the decomposition of carbonate-type byproducts and electrolyte. [ 31 ] |
 | Fig. 11. Proposed charging processes for Li 2 O 2 , with disc (gray/red, typical dimensions ∼ 50 to 200 nm) or particle (gray/blue, typical dimensions < 20 nm) morphologies overlaid. Discs’ surfaces are largely O-rich (0001) with LiO 2 -like surface species, while particles consist of less O-rich (more stoichiometric) Li 2 O 2 surfaces. During the initial stage of charging (to ∼ 800 mA·h/g C for discs and to ∼ 600 mA·h/g C for particles), both discs and particles exhibit a sloping voltage profile attributed to solid solution-like surface de-lithiation. Upon further charging, discs and particles exhibit a voltage plateau at ∼ 3.4 V vs. Li, corresponding to bulk oxidation via a two-phase process, e.g., between Li 2 O 2 and LiO 2 . [ 30 ] |
Another key challenge of the aprotic Li-O 2 batteries is their high recharging over-potential (usually > 1 V), [ 39 – 43 ] corresponding to slow kinetics and easily leading to serious side reactions. So it is imperative to understand the kinetics of Li 2 O 2 oxidation in aprotic Li + electrolytes. The kinetics of OER is affected by the current density and morphology of the discharge products. Adams et al . [ 16 ] demonstrated that the current density of discharge indirectly influences the charging over-potential by determining the nature and morphology of the Li 2 O 2 . The charging profiles (Fig.
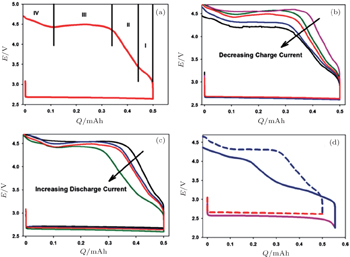 | Fig. 12. (a) A discharge–charge curve showing the regions of the charge portion; (b) cells discharged at 25 mA/cm 2 and then charged at different rates from 5–100 mA/cm 2 (colors of curves listed below); (c) cells discharged at different rates from 5–50 mA/cm 2 (colors of curves listed below) and then charged at 25 mA/cm 2 ; and (d) comparison of a cell fully discharged at 100 mA/cm 2 (pink curve) and then charged at 10 mA/cm 2 with a cell discharged at 25 mA/cm 2 to a similar capacity (red dotted curve) and then charged at 10 mA/cm 2 . In panels (b) and (c), black = 5 mA/cm 2 , blue = 10 mA/cm 2 , red = 25 mA/cm 2 , green = 50 mA/cm 2 , and pink = 100 mA/cm 2 . [ 16 ] |
Recently, Lu et al . [ 31 ] investigated the reaction kinetics of the charging reactions of aprotic Li-O 2 batteries and found that the OER kinetics is much slower than ORR in Li-O 2 batteries. During Li-O 2 battery charging, OER occurs at high over-potentials (0.4–1.2 V), where the kinetics is sensitive to discharge/charge rates and catalysts, which can be ascribed to the oxidation of bulk Li 2 O 2 particles (Fig. 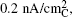
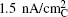
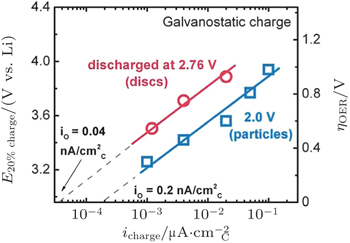 | Fig. 13. Tafel plot of galvanostatic charge voltage vs. carbon true surface area-normalized current for electrodes discharged under potentiostatic conditions at 2.76 V or 2.0 V vs. Li to 1000 mA·h/g C . The right-hand axis shows the OER over-potential referenced to the thermodynamic potential of Li 2 O 2 , E o (Li 2 O 2 ) = 2.96 V vs. Li. [ 44 ] |
A few in situ and ex situ research facilities having the ability to visualize the Li-O 2 reaction with nanometer resolution were employed to have a closer look at the charging process. [ 31 , 43 – 47 ] For instance, Zhong et al . [ 35 ] initially studied the electrochemical oxidation process of Li 2 O 2 using in situ TEM. Figure
 | Fig. 14. In situ TEM oxidation of Li 2 O 2 particles. (a) Schematic illustration of the in situ TEM microbattery superimposed over a low magnification TEM image of a solid electrolyte-coated Si nanowire contacting a single Li 2 O 2 particle. (b) Higher magnification TEM image of the particles in panel (a), showing a MWCNT bundle contacting two physically separated Li 2 O 2 particles labeled as particles 1 and 2, respectively. (c)–(g) Oxidation of particles 1 and 2 during application of a 10 V cell potential to the MWCNT/Li 2 O 2 positive electrode against the Si NW negative electrode. [ 35 ] |
By constructing an all-solid-state Li-O 2 battery in an environmental scanning electron microscope, direct visualization of the discharge and charge processes of the battery was achieved by Zheng et al . [ 48 ] Different morphologies of the discharge product were observed, including spheres, conformal films, and red-blood-cell-like shapes with the particle size up to 1.5 μm; whereas upon charging, the decomposition initiated at the particle surface and continued along a certain direction, instead of from the contact point at electrode (Fig.
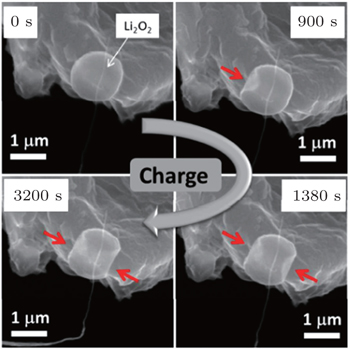 | Fig. 15. Charge processes of the Li-O 2 battery. Images captured at 0 s, 900 s, 1800 s, and 3200 s show the decomposition process of the spherical particle. Eight volts was applied on SACNT vs. Li metal to initiate the charge process. Red arrows indicate the position where the particle decomposed. Note that the electron beam was on only during image acquisition, to minimize the irradiation effect. [ 48 ] |
In situ AFM has also provided clear-cut evidence for decomposition of Li 2 O 2 during the charging reaction. Real-time and in situ views of the Li 2 O 2 decomposition using electrochemical AFM (EC-AFM) are presented in Fig.
 | Fig. 16. In situ and sequential AFM topographic images of Li 2 O 2 nanoplates on HOPG upon OER in Li-O 2 cell. (a) Li 2 O 2 nanoplates acquired via the galvanostatic discharge at a cutoff potential of 2.2 V. (b) Potential-dependent view of HOPG electrode from 2.8 V (bottom) to 4.0 V (middle to top) at a sweeping rate of 5 mV/s. (c) Clean HOPG electrode at 4.0 V. The scale bars are 500 nm. [ 49 ] |
Among relatively stable aprotic electrolytes, Li 2 O 2 has been widely identified as the main discharge product formed in the porous cathode of aprotic Li-O 2 batteries. As Li 2 O 2 is an insulator, poor conductivity eventually leads to the so called sudden death at the end of the discharge process. These observations have prompted researchers to investigate the electron and ion transport in Li 2 O 2 , which are very important for understanding the discharge and charge chemistries involved in Li 2 O 2 formation and decomposition mechanisms. [ 50 – 54 ] However, the mechanisms of charge transport through Li 2 O 2 remain elusive. Luntz et al. [ 54 ] presented both experimental and theoretical evidences that hole tunneling generally dominates charge transport through Li 2 O 2 in Li-O 2 discharge at practical battery current densities. Others [ 51 , 55 – 58 ] suggested that diffusion of isolated small polarons trapped at Li vacancies or charged defects governs the charge transport within Li 2 O 2 . Taken together, these observations motivate the understanding of the mechanism of charge transport through Li 2 O 2 mainly determined by two factors: [ 50 , 54 ] (i) the alignment of the Li 2 O 2 bands relative to the Fermi level in Li 2 O 2 in the electrochemical cell, and (ii) the formation energies, densities, and mobilities of various charged carriers (polarons, vacancies, impurities) at the battery potential.
Figure
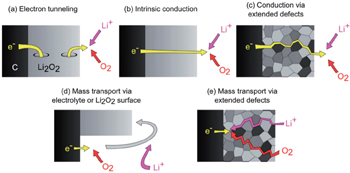 | Fig. 17. Possible discharge mechanisms for a Li-O 2 cell. [ 51 ] |
Figure
Turning to OER, Figure
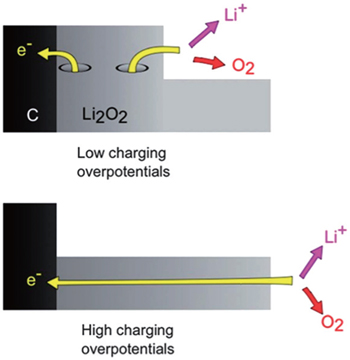 | Fig. 18. Proposed two-stage recharge mechanism for a Li-O 2 cell. [ 51 ] |
This review summarizes the current state of knowledge and research about the fundamental aspects of the oxygen electrode reaction in aprotic Li-O 2 batteries. For the ORRs, O 2 is first reduced via a one-electron process to 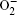
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 |


