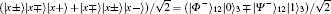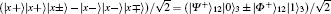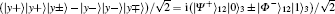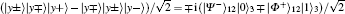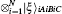†Corresponding author. E-mail: yangh@korea.ac.kr
*Project supported by the Research Foundation of Korea University.
In this paper, we suggest a controlled mutual quantum entity authentication protocol by which two users mutually certify each other on a quantum network using a sequence of Greenberger–Horne–Zeilinger (GHZ)-like states. Unlike existing unidirectional quantum entity authentication, our protocol enables mutual quantum entity authentication utilizing entanglement swapping; moreover, it allows the managing trusted center (TC) or trusted third party (TTP) to effectively control the certification of two users using the nature of the GHZ-like state. We will also analyze the security of the protocol and quantum channel.
In network communication, it is very important to develop a system or protocol in which transferred information is received by only the authenticated user. The receiver identifies the creator of the information and verifies whether it was falsified. Authentication provides secure network communication by certifying messages, entities, and keys. In particular, entity authentication, such as password authentication, one-time password authentication, challenge-response authentication, bit commitment, and so on, refers to a series of processes for certifying entity identification.[1– 4]
When identification[1] is used as entity authentication it refers to verification, identity confirmation, or identity certification in a narrow sense, such as a user identification code, user name, user ID, or ID number, which are used to verify the authenticated user in a multiuser computer environment or communication network system. In a broad sense, it is a form of identification certification that is required for accessing online information service systems, such as online databases. To access and log into the network, the user ID and corresponding password or key are always necessary to accurately verify the identification. For example, at the International Organization for Standardization (ISO) and the International Electro-technical Commission (IEC), only entity authentication, specifically the meaning of a series of phrases, is used to verify identity.[5]
Since Bennett and Brassard suggested quantum key distribution, [6] many researchers of quantum communication protocols have suggested quantum entity authentication protocols[7– 11] under the names of quantum identification or quantum identity authentication, as well as multiparty simultaneous quantum entity protocols, [12– 16] in which a trusted center (TC) or trusted third party (TTP) effectively certify users in the quantum network. Furthermore, various bidirectional quantum communication protocols[17– 28] for bilaterally transmitting or sharing quantum information, such as bidirectional quantum key distribution, bidirectional quantum communication, bidirectional quantum teleportation, and bidirectional quantum secret sharing, have been proposed.
Based on the above bidirectional quantum communication protocols, we conceived a bidirectional quantum entity authentication protocol using entanglement swapping. In this protocol, TC (or TTP) can control all of the mutual authentication phases, including entanglement swapping in a quantum network[29– 34] which utilizes Greenberger– Horne– Zeilinger (GHZ)-like states, as in controlled quantum teleportation protocols, [35– 37] quantum secret sharing protocols, [38– 41] controlled direct communication, [42, 43] and remote state preparation.[44] To enhance security, TC (or TTP) randomly inserts a decoy qubit before the entity authentication of two users.[45, 46]
In the entity authentication protocol, an entity is commonly referred to as an individual or a machine, an entity that attempts to prove its identity is a prover or claimant, and an entity that verifies another’ s identity is a verifier. One of several authentication protocols, challenge-response authentication is widely used in classical entity authentication.
Challenge-response authentication can be designed using a symmetric-key cipher, asymmetric-key cipher, digital signature, and keyed-hash functions.[1– 4] Figure 1 depicts a simple example of challenge-response authentication using a symmetric-key cipher.
The nonce (random number), RB, and timestamp T in Figs. 1(a) and 1(b) are used to maintain the freshness of the entity authentication process, which differs from message authentication. Message authentication is completed by verifying the message integrity and identifying the message generator. In entity authentication, on the other hand, the entity attempting access of the network system is to be authenticated in real time; accordingly, freshness or timeliness is indispensable. In contrast, most quantum communication is achieved in a short time period; it is therefore not necessary to consider freshness or timeliness in quantum entity authentication. This marks the difference between classical entity authentication and quantum entity authentication.
By adding authentication processes to the unidirectional authentication shown in Fig. 1, bidirectional authentication is additionally possible, as shown in Fig. 2.[1– 4]
 | Fig. 1. Challenge-response authentication using a symmetric-key cipher.[1– 4] In phase 1 in panel (a), prover Alice transmits her identification IDA to verifier Bob to request entity authentication. In challenge phase 2 of panel (a) Bob sends a nonce (random number) RB to Alice. In response phase 3 of panel (a), Alice demonstrates that she is sharing the secret key, kAB, with Bob by transmitting to Bob the encrypted random number, kAB(RB). The nonce, RB, is renewed in each session. In panel (b), Alice shows that she is also sharing the secret key, kAB, with Bob. Unlike Bob, Alice completes the entity authentication by transmitting only once the encrypted number, kAB (IDA, T), of her identification IDA and timestamp T using the secret key, kAB. If timestamp T is not agreed upon in advance, Bob rejects Alice’ s authentication. |
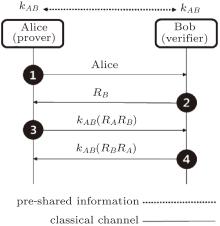 | Fig. 2. Bidirectional challenge-response authentication using a symmetric-key cipher.[1– 4] As in Fig. 1(a), Alice and Bob, respectively, check the nonce (random number) RA and RB, and mutually verify the unidirectional authentication using the nonce. In phase 3, Alice generates encrypted random numbers kAB (RARB) and responds to Bob’ s challenge, while simultaneously challenging Bob to identification. In phase 4, Bob generates kAB (RBRA) and responds to Alice’ s challenge, thereby completing the certification process. |
Four mutually orthonormal Bell states are expressed as follows:
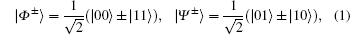
where | 0⟩ and | 1⟩ are two eigenstates of Pauli operator σ z or horizontally and vertically polarized states of the photon, respectively.
Quantum entanglement swapping plays an important role in quantum communication. Using quantum entanglement swapping, we can establish two entangled quantum systems without direct interaction. Suppose that Alice prepares | Ψ + ⟩ 1A1B and | Ψ + ⟩ 2A2B, and sends Bob two qubits, 1B and 2B. Then, two distant users, Alice and Bob, share two entangled states, | Ψ + ⟩ 1A1B ⊗ | Ψ + ⟩ 2A2B, where Alice has qubits 1A and 2A, and Bob has 1B and 2B. This state can be rearranged as follows:

If Alice measures qubits 1A and 2A with the Bell basis, | Ψ + ⟩ 1A1B ⊗ | Ψ + ⟩ 2A2B in Eq. (2) collapses into| Φ + ⟩ 1A2A| Φ + ⟩ 1B2B, | Φ − ⟩ 1A2A| Φ − ⟩ 1B2B, | Ψ + ⟩ 1A2A| Ψ + ⟩ 1B2B, or | Ψ − ⟩ 1A2A| Ψ − ⟩ 1B2B by equal probability of 1/4. Due to the Bell measurement, the entanglements between qubits 1A and 1B, and between qubits 2A and 2B, are swapped to entanglements between qubits 1A and 2A, and between qubits 1B and 2B.[12, 21, 31] Figure 3 illustrates the entanglement swapping of Bell states in three steps. The Bell measurement outcomes on four different initial combinations of Bell states are summarized in Table 1.
 | Fig. 3. Schematic representation of the entanglement swapping of Bell states. (a) Alice prepares two entangled states. A dot (• ) represents each qubit and a line (− ) denotes entanglements. (b) Alice sends Bob one qubit in each entanglement pair. (c) Alice and Bob respectively perform Bell measurements on each of their own qubits. Consequently, the entanglements between Alice and Bob are swapped.[23] |
| Table 1. Measurement outcomes of the entanglement swapping on sixteen combinations of four Bell states. |
The symbol ID + + denotes the set of four possible outcomes {(| Φ + ⟩ 1A2A, | Φ + ⟩ 1B2B), (| Φ − ⟩ 1A2A, | Φ − ⟩ 1B2B), (| Ψ + ⟩ 1A2A, | Ψ + ⟩ 1B2B), and (| Ψ − ⟩ 1A2A, | Ψ − ⟩ 1B2B)} with an equal probability of 1/4. Similarly, ID + − represents {(| Ψ + ⟩ 1A2A, | Ψ − ⟩ 1B2B) (| Φ − ⟩ 1A2A, | Φ + ⟩ 1B2B), (| Φ + ⟩ 1A2A, | Φ − ⟩ 1B2B), and (| Ψ − ⟩ 1A2A, | Ψ + ⟩ 1B2B)}, and Rev + + symbolizes {(| Φ + ⟩ 1A2A, | Ψ + ⟩ 1B2B), (| Φ − ⟩ 1A2A, | Ψ − ⟩ 1B2B), (| Ψ + ⟩ 1A2A, | Φ + ⟩ 1B2B), and (| Ψ − ⟩ 1A2A, | Φ − ⟩ 1B2B)}. Rev + − describes {(| Φ + ⟩ 1A2A, | Ψ − ⟩ 1B2B) (| Φ − ⟩ 1A2A, | Ψ + ⟩ 1B2B), (| Ψ + ⟩ 1A2A, | Φ − ⟩ 1B2B), and (| Ψ − ⟩ 1A2A, | Φ + ⟩ 1B2B)}.[23, 47]
A GHZ-like state consisting of

is expressed as follows:[26, 32]
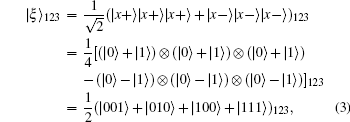
where | x+ ⟩ and | x− ⟩ are two eigenstates of σ x, and | 0⟩ and | 1⟩ are eigenstates of σ z. Another GHZ-like state consisting of
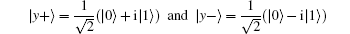
is represented as follows:

where | y+ ⟩ and | y− ⟩ are two eigenstates of σ y. Various GHZ-like states can be generated, as shown in Table 2.
Table 2. Various GHZ-like states:   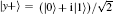  |
By utilizing GHZ-like states in quantum information transmission or quantum communication, we can add a controller that controls or regulates the communication between two users. In practice, GHZ-like states have been used in controlled quantum teleportation protocols, [35– 37] quantum secret sharing protocols, [38– 41] controlled direct communication, [42, 43] and remote state preparation.[44] We can understand how TC (or TTP) is authorized as a controller in controlled quantum teleportation or controlled secure direct communication by rearranging the GHZ-like state in three different forms as follows:
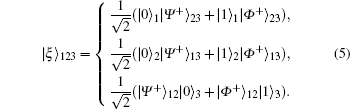
If TC measures the first qubit in Eq. (5) in a σ z basis, then the second and third-qubits will have a 50% chance of being in an entangled state, | Ψ + ⟩ 23 or | Φ + ⟩ 23. Therefore, the entangled state of two users who share the second and third qubits is determined by the measurement result of the controller who owns the first qubit.
Let us consider a composite system consisting of two GHZ-like states and an entanglement swapping on it. After performing a von Neumann measurement on one qubit of each GHZ-like state, we execute the entanglement swapping operation on the two Bell states as follows.
(I) A composite system of two GHZ-like states | ξ ⟩ 123 and | ξ ⟩ 456 are constructed as follows:

(II) If the third and sixth qubits of state | ξ ⟩ 123 ⊗ | ξ ⟩ 456 are measured in a σ z basis, it will be collapsed to one of | Ψ + ⟩ 12| Ψ + ⟩ 45, | Ψ + ⟩ 12| Φ + ⟩ 45, | Φ + ⟩ 12| Ψ + ⟩ 45, or | Φ + ⟩ 12| Φ + ⟩ 45 by a 25% probability, as shown in Table 3.
(III) We perform the entanglement swapping operation on the two entangled states in Table 3 as previously mentioned; the result is the same as that in Table 2.
| Table 3. If the third and sixth qubits of the composite system | ξ ⟩ 123 ⊗ | ξ ⟩ 456 are measured in a σ z basis, then | ξ ⟩ 123⊗ | ξ ⟩ 456 will be collapsed into | Ψ + ⟩ 12| Ψ + ⟩ 45, | Ψ + ⟩ 12| Φ + ⟩ 45, | Φ + ⟩ 12| Ψ + ⟩ 45, or | Φ + ⟩ 12| Φ + ⟩ 45 by a 25% probability. |
In addition to the above operation on the state in Eq. (5), various entanglement swapping operations on the 16 GHZ-like states in Table 2 are also possible.
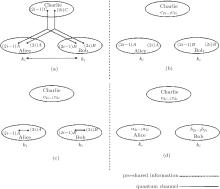
Suppose that two users, Alice and Bob, want to certify each other in the quantum network; the TC (TTP), Charlie, controls or regulates the mutual entity authentication between them. The controlled mutual quantum entity authentication consists of the respective prepare, security check and the entity authentication phases. Figure 4 schematically illustrates the protocol of the controlled mutual quantum entity authentication that we suggest.
P1 Alice and Bob share a secret key sequence, KAB = (k1, k2, … , kN), using QKD protocols, [6, 48] which securely distribute the keys.[49, 50] The sequence, KAB = (k1, k2, … , kN), is a classical bit sequence with the size of 2N; the elements are defined as ki ∈ {00, 01, 10, 11}. Key ki corresponds to Pauli operators, as follows:
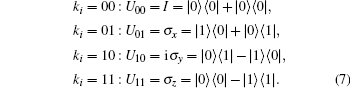
In our protocol, ki is the secret information for the mutual entity authentication of Alice and Bob.
P2 The controller, Charlie, prepares the sequence(| ξ ⟩ 1, | ξ ⟩ 2, … , | ξ ⟩ NE) consisting of N GHZ-like states follows Refs. [51]– [58] for entity authentication, which is shown as
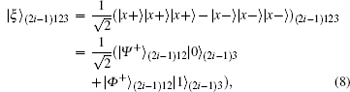
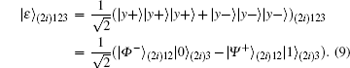
Charlie retains the third qubit, sends Alice the first qubit and Bob the second qubit, and then announces that he has transmitted the qubits to them. After transmission, the state is given as follows:
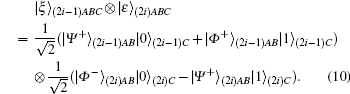
The subscript i in Eq. (10) designates the order in the sequence of the GHZ-like state, A, B, or C, showing the owner of the qubit. Transmitting N GHZ-like states to Alice and Bob, Charlie randomly inserts NC decoy qubits
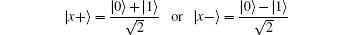
to detect the eavesdropping.[45, 46] Alice and Bob, who received the qubits from Charlie, notify each communication member through the public channel of their safe receipt.
S1 Confirming that Alice and Bob have safely received the qubit sequence, Charlie reveals the location of the decoy qubits.
S2 Alice and Bob execute the σ x basis {| x+ ⟩ , | x− ⟩ } measurement only on the decoy qubits received from Charlie and report the result. Charlie compares the initial states of the decoy qubits and the result outcomes from Alice and Bob; he then checks the eavesdropping.[45, 46]
E1 Charlie randomly chooses only one communication member, Alice or Bob, to apply the Pauli operator on the (2i − 1)-th or 2i-th state of Eq. (10). If Charlie chooses Alice, then Alice applies the Pauli operator corresponding to the classical bit, ki, to the (2i − 1)-th state, such as in Eq. (7). If Charlie chooses Bob, then Bob applies the Pauli operator corresponding to the classical bit, ki, to the 2i-th state of Eq. (10). When classical bit ki, which Alice and Bob share beforehand, is 10, the corresponding Pauli operator is iσ y(= U10). If Charlie chooses Alice, then Alice applies U10 to the (2i − 1)-th state | ξ ⟩ (2i − 1)ABC and Bob does not operate anything, as follows:
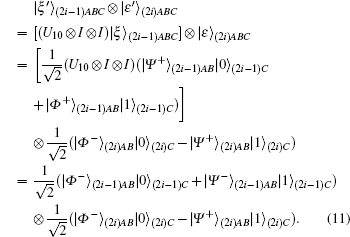
Through the public channel, Alice (or Bob) notifies Charlie that she (or he) has applied the Pauli operator.
E2 Charlie executes the σ z basis measurement on the (2i − 1)-th and 2i-th qubit of his own qubit sequence. He notifies Alice and Bob only about the fact that he performed this action. After Charlie’ s measurement, the GHZ-like states of Eq. (11) collapse into | Φ − ⟩ (2i− 1)AB| Φ − ⟩ (2i)AB, | Φ − ⟩ (2i− 1)AB| Ψ + ⟩ (2i)AB, | Ψ − ⟩ (2i− 1)AB| Φ − ⟩ (2i)AB, or | Ψ − ⟩ (2i− 1)AB | Ψ + ⟩ (2i)AB by a 25% probability, and Alice and Bob share one of the pairs of entangled states. For example, when the measurement outcomes are | 0⟩ (2i− 1)c and | 1⟩ (2i)c, Alice and Bob share | Φ − ⟩ (2i− 1)AB ⊗ | Ψ + ⟩ (2i)AB. The shared entangled state | Φ − ⟩ (2i− 1)AB ⊗ | Ψ + ⟩ (2i)AB can be rearranged as follows:
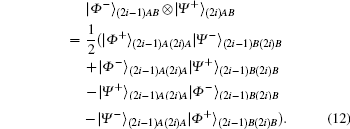
It is a superposed state of entangled states
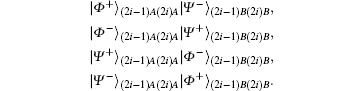
E3 By the Bell measurement performed by Alice and Bob, the entangled states between Alice and Bob | Φ − ⟩ (2i− 1)AB ⊗ | Ψ + ⟩ (2i)AB are collapsed into a product state of Alice’ s entangled state and Bob’ s entangled state, which is one of
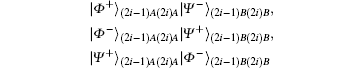
or | Ψ − ⟩ (2i− 1)A(2i)A| Φ + ⟩ (2i− 1)B(2i)B. After this entanglement swapping, Alice and Bob announce their measurement outcomes, a2i− 1a2i and b2i− 1b2i (aj& bj ∈ {0, 1}, j = 2i − 1 or 2i), as follows:
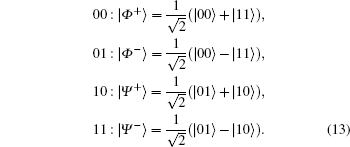
Charlie reveals the measurement outcome of classical bit c2i− 1c2i acquired in phase E2, where c2i− 1c2i ∈ {00, 01, 10, 11}. Both Alice and Bob confirm whether their classical bits, a2i− 1a2i and b2i− 1b2i, correctly correspond to the revealed classical bit, c2i− 1c2i, as shown in Table 4.
| Table 4. ki is a secret key shared between Alice and Bob. a2i − 1a2i, b2i − 1b2i, and c2i − 1c2i are measurement results produced by Alice, Bob, and Charlie, respectively. For example, if ki is 10, c2i − 1c2i is 01, and a2i − 1a2i is 11, then b2i − 1b2i should be 00. |
In the example of phase E3, because the key, ki, which Alice and Bob share, is 10, and Charlie’ s measurement result c2i− 1c2i is 01, the pair of measurement outcomes of Alice and Bob, (a2i− 1a2i, b2i− 1b2i), must be one of the following four pairs: {(00, 11), (01, 10), (10, 01), (11, 00)}. If the calculated results a2i− 1a2i and b2i− 1b2i in phase E3 are consistent with Table 4, then the entities Alice and Bob are successfully authenticated. Otherwise, the entity authentication fails.
Two possible kinds of attack exist in our protocol. One is an internal attack in which communication users, Alice and Bob, try to verify each other without the controller, Charlie. The other is an external attack in which a third party, who is not a legitimate communication member, impersonates Alice, Bob, or Charlie. The internal attack is simulated as a double CNOT attack or entanglement attack; [15, 46, 47] the external attack is simulated as an intercept and resend attack.[12, 23, 44]
In explaining a double CNOT attack or entanglement attack, we suppose that, as a matter of convenience according to previous papers, the person who internally attacks Alice or Bob is Eve. The internal attacker, Eve, prepares ancilla states | 0⟩ (2i − 1)E ⊗ | 0⟩ (2i)E. The GHZ-like states | ξ ⟩ (2i − 1)ABC ⊗ | ε ⟩ (2i)ABC and ancilla states | 0⟩ (2i − 1)E ⊗ | 0⟩ (2i)E form a composite system, | Ω ⟩ (2i − 1)ABCE ⊗ | X⟩ (2i)ABCE, as follows:
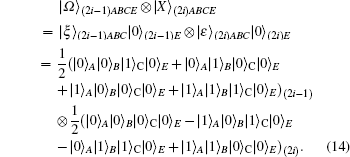
Eve applies the CNOT operation CAE and CBE, where Alice’ s and Bob’ s states are control qubits, and Eve’ s state is a target qubit on the composite system | Ω ⟩ (2i − 1)ABCE ⊗ | X⟩ (2i)ABCE of Eq. (16) as follows:

When Eve’ s measurement outcome of ancilla states and Charlie’ s measurement outcome in Eq. (15) are e2i− 1e2i and c2i− 1c2i, respectively, e2i− 1e2i is identical to (c2i− 1 ⊕ 1)(c2i), as shown in Table 5.
| Table 5. Charlie’ s measurement outcome c2i − 1c2i and Eve’ s measurement outcome e2i − 1e2i. |
As a result, the internal attacker, Eve, can execute entity authentication without Charlie’ s assistance. Therefore, for the security of the protocol, in the preparation phase, Charlie sends Alice and Bob both N GHZ-like state(s) and NC decoy qubits of
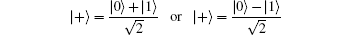
in random order.[45, 46] After distributing N entangled states and NC decoy qubits and completing the security check phase, the probability of detecting eavesdropping D is given as follows:
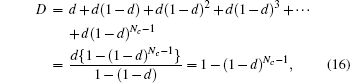
where d is the probability of detecting eavesdropping by checking one decoy qubit. If Charlie increases the number of decoy qubits NC for the security of the communication channel, then the probability D of detecting Eve’ s intervention would be close to unity regardless of the value of d.
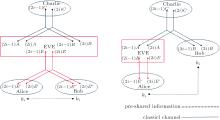
The external attacker, Eve, can either intercept two pairs of qubits, which are transmitted to Alice and Bob, and send two pairs of another GHZ-like state prepared as in Fig. 5(a), or intercept one pair of qubits, which are transmitted to Alice or Bob, and send a Bell state prepared as in Fig. 5(b). Likewise, with the intervention of Eve, the communication members can find, just by comparing the measurement outcome before entity authentication phase, whether there is an external attacker, Eve, since there is no correlation in the measurement outcome of the qubit which Alice, Bob, and Charlie, respectively, own. The probability of detecting Eve’ s existence is 1 − (1/4)n, where n is the number of GHZ-like states.
If n is big enough, then the probability of detecting Eve’ s existence approaches to unity.[12, 23, 44] Furthermore, we use the decoy qubits to prevent both internal and external attack. The entangled state’ s correlation check method and the decoy qubit insert method guarantee the security of the communication channel.
The controlled mutual quantum entity authentication protocol that we proposed is adequate for use in a quantum network system in which no quantum communication line exists between two users, Alice and Bob. The communication line between two users is established through the transmission of a GHZ-like state by TC (or TTP), Charlie. TC performs only two von Neumann measurements to control the authentication process using the GHZ-like state, and the two users execute entanglement swapping, which makes mutual entity authentication possible. Also, like our protocol to build a quantum network system, there are a variety of quantum protocols which teleport quantum information or confirm pre-shared classical information. We compared these quantum protocols with our protocol in Table 6. Especially, Deng et al.’ s controlled-quantum teleportation[35] which uses GHZ states to build a quantum network and teleports an unknown two-particle state by the help of an agent. Their controlled-quantum teleportation protocol can be applied to quantum secret sharing protocols, [35] and there are many other similar quantum secret sharing protocols[38– 41]. If Deng et al.’ s controlled-quantum teleportation replaces an unknown two-particle state with pre-shared secret information, then their protocol is similar to our entity authentication protocol. However, a controller in our protocol performs von Neumann measurement instead of Bell measurement. By the help of a controller, a mutual authentication of a prover and a verifier is possible in our protocol.
| Table 6. Comparison of quantum protocols based on quantum network system. |
For mutual authentication, two users must know the measurement outcome of TC (of TTP) in addition to the shared secret information. This is because the measurement outcome and its corresponding entangled states are completely random. In our protocol, the security checking process using the decoy qubit can prevent the double CNOT attack, which is the primary attack attempted by an adversary to obtain the measurement result of TC.
To access the quantum network system, the user must present his or her ID and corresponding password, which can be identified by TC. In our protocol, the secret key, ki, plays the role of the password, which is shared in advance between users. The GHZ-like state in our protocol is analogous to the login webpage of a financial company or portal service. Anyone can participate in the authentication phase with the transmitted entangled states from TC in our protocol, just as anyone can access a login webpage— but no one logs in without a legitimate ID and password.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|