An original numerical model, based on the standard Berg model, is used to simulate the growth mechanism of N-doped VO x deposited with changing oxygen flow in the reactive gas mixture. In order to compare with the numerical model, N-doped VO x films are prepared by reactive magnetron sputtering from a metallic vanadium target immersed in a reactive gas mixture of Ar+O2+N2. Both experimental and numerical results show that the addition of N2 to the process alleviates the hysteresis effect with respect to the oxygen supply. Film compositions obtained from the XPS analysis are compared to the numerical results and the agreement is satisfactory. The results also show that the compound of VN is only found at very low O concentration because of the replacement reaction of VN by O2 atoms with higher oxygen flow rate.
Vanadium oxides have attracted much attention over the past few decades because of their thermochromic properties.[1– 4] VO2 exhibits an abrupt semiconductor metal transition at about 68 ° C, accompanied by sharp drop in resistivity and IR transmittance.[5, 6] The optical transmission and reflection spectra of V2O5 can be changed by heating or laser irradiation due to the thermochromism, which shows potential application in the field of information storage or displays.[7] The physical and chemical parameters of vanadium oxides can be modified by doping with other elements. For example, doping VO2 thin films with transition metals is known to largely affect the properties of the metal– insulator transition (MIT).[8, 9]
Thin films doped with vanadium oxides can be prepared by various methods, including reactive sputtering, [10] sol-gel method, [11] chemical vapor deposition, [12] ion implantation, [13] pulsed laser deposition, [14] etc. Among these methods, reactive sputtering has gained significant importance because it enables control of the structure, composition, and properties of VOx films by adjusting the deposition conditions. This process is very nonlinear and usually exhibits a hysteresis behavior with respect to the reactive gas flow. In order to understand this phenomena, Berg et al.[15, 16] proposed a qualitative model to describe the reactive sputtering deposition at steady state. Recently, the extensions to this model have been published, [17– 22] such as deposition with two gases.[21, 22]
However, to our knowledge, there are no studies on reactive sputtering of multi-component thin films such as VOx using a doping gas. Studies of nitrogen-doped vanadium oxide films are attracting more attention since it potentially eliminates the hysteresis effect and improves the film properties.
In this paper, the effect of the reactive gas mixture on the hysteresis effect during the reactive sputtering deposition of N-doped VOx thin films is investigated both from experimental data and numerical modeling. Based on the modeling results, the effect of doped nitrogen on the compound fractions at the collecting area is also discussed. The overall composition of N-doped VOx is generally a mixture of V, V2O3, VO2, V2O5, and VN. During simulations, the film structure is assumed to be composed of a mixture of V, VN, V2O5, and suboxides such as V2O3 and VO2. Some other phenomena, such as replacement reactions caused by oxidation of the nitride layers and reduction of compounds caused by sputtering, are also included into the model.
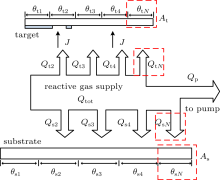
The mathematical model describing the sputtering system is shown in Fig. 1. The total input rate of the reactive gas (oxygen) is denoted as Qtot. The target surface can then be divided into five parts (see Fig. 1). The fractions of V, V2O3, VO2, V2O5, and VN at the target will be called θ t1, θ t2, θ t3, θ t4, and θ tN, respectively. θ s1, θ s2, θ s3, θ s4, and θ sN are fractions of collecting area covered by V, V2O3, VO2, V2O5, and VN, respectively.
It is assumed that the gettering of reactive gas (O2 and N2 onto metal contributes to the formation of suboxide V2O3 or VN on the target, depending on the probability of these two reactions, which will increase θ t2 or θ tN, respectively. Further attachment (by oxygen) onto this suboxide V2O3 contributes to form the VO2, causing an increase in θ t3 but a decrease in θ t2. The superoxide V2O5 is formed by the reaction of the oxygen and VO2. For the metal vanadium atoms sputtered from the target, if the atom comes from the fraction of θ t1 and deposits on the substrate surface which previously consisted of VOx (V2O3, VO2, V2O5, and VN), then the fraction of θ s1 will increase and the fraction of (1-θ s1) will decrease. Furthermore, when the VOx particle sputtered from target deposit on the substrate which previously consisted of VOi (i! = x), then the corresponding fraction of θ si will decrease and the fraction of VOx will increase. However, the fraction of flux (J/q)Ytiθ tiAt deposited onto the fraction θ si of the collecting area As will not change the value of θ s1. Adding elemental non-reacted target atoms to an area that already consists of non-reacted atoms also does not change θ s1. As we have mentioned, it is assumed that oxygen can convert nitride to oxide, with a certain probability. Therefore, β 1, β 2, and β 3 are the replacement coefficient for replacement of compound VN by compound of V2O3, VO2, and V2O5, respectively.
The following simulation parameters are used in this work: α t1 = 0.8, α t2 = 0.8, α t3 = 0.8, α t4 = 0.8, α tN = 0.6, α s1 = 1, α s2 = 1, α s3 = 1, α s4 = 1, α sN = 0.8. Yt1 = 0.6, Yt2 = 0.3, Yt3 = 0.2, Yt4 = 0.2, YtN = 0.2. γ 1 = 1, γ 2 = 0.4, γ 3 = 0.4, γ 4 = 0.4, γ N = 0.4, γ = 1. l1 = 0, l2 = 3, l3 = 4, l4 = 5, l5 = 2. β 1 = 0.08, β 2 = 0.15, β 3 = 0.08, U0 = 300 V. Target area At = 260 cm2, gas temperature T = 300 K, pumping speed S = 0.2 m3/s.
By making the assumptions above, in combination with the simplifications presented earlier, the balance equations for the conditions on the target should be rewritten as
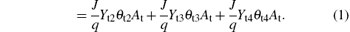
Here J is the ion-current density; q is the elementary electronic charge; Yt2, Yt3, and Yt3 are the sputtering yield of the V2O3, VO2, and V2O5, respectively; α t1 is the probability (sticking coefficient) for an oxygen molecule to react with a vanadium atom that comes from the θ t1 fraction of the target; α tN is the sticking coefficient for nitrogen; At is the target area; l2 and l5 are the stoichiometry of the V2O3 and VN, respectively; and F1 and F2 represent oxygen and nitrogen molecules/(unit area and time), respectively.
Equation (1) determines the balance of the vanadium atom fraction (θ t1) on the target. For simplicity, the sputtered material from the surface fraction (J/q)Yt2θ t2At + (J/q)Yt3θ t3At + (J/q)Yt4θ t4At is assumed to be sputtered as molecules, irrespective of whether the material is ejected in atomic or molecular form. The only way that sputtered compound molecules may be replaced is by reactions between neutral reactive gas molecules (O2, N2 and the elemental non-reacted vanadium atoms,
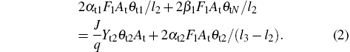
Moreover, equation (2) determines the balance of the fraction of θ t2 on the target. Here, l3 is the stoichiometry of the VO2. The reaction between elemental target atoms and the reactive gas atoms (which occurs on the compound fraction θ t1) will contribute to an increase in the value of θ t2. Besides, the replacement of nitride by oxygen, which converts compound VN into compound V2O3, will also increase the fraction of V2O3. On the other hand, the compound V2O3 is sputtered from the surface fraction θ t2, decreasing the fraction of θ t2. Furthermore, attaching the oxygen to V2O3 will contribute to a decrease in θ t2 as well.
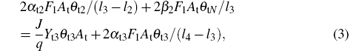

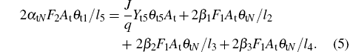
Similar to Eqs. (1) and (2), equations (3)– (5) determine the balance of the fraction of θ t3, θ t4, and θ tN, respectively. Here, l4 is the stoichiometry of the V2O5. Note that all the compound fraction sums to unity, namely,
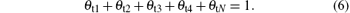
The expressions for θ t1, θ t2, θ t3, θ t4, and θ tN can be obtained by solving Eqs. (2)– (6).
At a steady state, the contributions supporting an increase in θ si must be identical to the contributions that support a decrease in θ si. This leads to the following balance equations for the collecting area As:
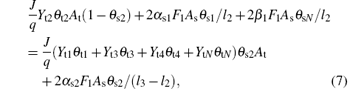
where α s1, α s2, and α s3 are the probability (sticking coefficients) for the oxygen molecule to react with V, V2O3, and VO2 on the substrate, respectively.
Equation (7) determines the balance of the fraction θ s2 on the substrate. The fraction of flux (J/q)Yt2θ t2At that is deposited onto the fraction (1-θ s2) will increase the value of θ s2. Obviously, the reactions between O2 and vanadium atoms at the substrate surface will increase θ s2. Moreover, the replacement of nitride by oxygen 2β 1F1Asθ sN / l2, which converts compound VN into compound V2O3, will also increase the fraction of V2O3. The fraction of flux (J/q)(Yt1θ t1 + Yt3θ t3 + Yt4θ t4 + YtNθ tN deposited onto the fraction (θ s2) will contribute to a decrease in θ s2. The number of molecules which convert into VO2 by oxygen is denoted by 2α s2F1Asθ s2 /(l3 − l2 ). The reaction between elemental non-reacted atoms and oxygen will also decrease the value of θ s2.
Likewise, the steady-state equation for the fraction of VO2, V2O5, and VN on the substrate may therefore be defined as
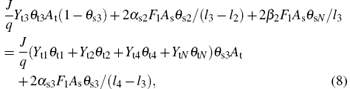
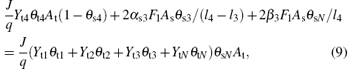
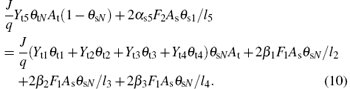
Finally, the sum of fractions (θ s1, θ s2, θ s3, θ s4, θ sN) is equal to 1, like that in the case of the target surface,
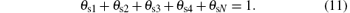
Based on the fact that target voltage U depends both on the secondary emission coefficient γ and the degree of target poisoning. Pflug et al.[23] suggested the following expression:
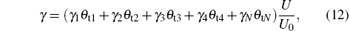
in which γ 1, γ 2, γ 3, γ 4, and γ N are the secondary electron emission coefficients, respectively, at the V, V2O3, VO2, V2O5, and VN on the target surface, and U0 is a reference voltage required for keeping the equation dimensionless. Thus, by this equation, U is calculated as functions of θ t1, θ t2, … , θ tN.
Compound formation by reaction between O2 and vanadium atoms, compound V2O3, and compound VO2 at the target will consume reactive gas molecules Qt1, Qt2, and Qt3, reactively. Thus, the consumption (number of oxygen molecules per unit time) at the target Qt can be obtained from

While the consumption Qs at the collecting area As can be expressed by
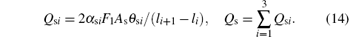
Here, Qs1 is reactive gas molecules consumed by oxygen molecules and vanadium atoms at collecting area. Qs2 is the oxygen molecules consumed by V2O3 compound. The other part Qs3 is the oxygen molecules consumed by the VO2 compound.
The remaining part Qp of the oxygen will escape from the processing chamber through the pumping system,
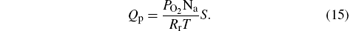
Here, PO2 is the partial pressure of oxygen, Na is the Avogadro constant, Rr is the general gas constant, T is the temperature, and S is the pumping speed.
The total flow rate of oxygen is denoted as Qtot-O2
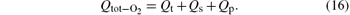
Similar to the oxygen gettering process, the flow rate of nitrogen is determined by
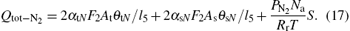
Here, PN2 is the partial pressure of nitrogen. The expressions for oxygen flow (Qtot– O2) and nitrogen flow (Qtot– N2) versus target voltage (U) can be obtained by numerical calculation based on Eqs. (1)– (17).
N-doped VOx thin films were deposited by DC reactive magnetron sputtering in a custom-built vacuum system. A water-cooled rectangle planar vanadium metal target, with a purity level of 99.99% , was used in these experiments. The deposition chamber was evacuated to a base pressure of about 1.0× 10-4 Pa by a combination of turbomolecular and rotary vane pumps. Argon, oxygen, and nitrogen flow were controlled by using independent mass flow controllers, and the argon flow was kept constant at 100 sccm. The oxygen flow and nitrogen flow were varied from 1.0 to 6.0 sccm and 0 to 4.0 sccm, respectively. In order to ensure reproducible results of the reactive sputtering between runs, the vanadium target was first pre-sputtered by argon plasma for 15 min, and then oxygen injection was kept on for 15 min until equilibrium is reached in the argon/oxygen mixture.
The x-ray photoelectron spectroscopy (XPS) spectra were taken by using XSAM800 system (Kratos Ltd., Al Kα x-ray source without monochromatization, the base pressure of the ultrahigh vacuum chamber is lower than 3× 10-7 Pa, binding energies (BE) are determined by using C1s peak at 284.8 eV as a reference, the resolution is 0.9 eV/104 counts per second).
The numerical and experimental results for the target voltage as functions of oxygen flow rate at different N2 flow rates are shown in Figs. 2(a) and 2(b). It can be seen that there is a pronounced difference in hysteresis width for the curves without N2. The appearance of the hysteresis loop is caused by the large difference between the consumption of reactive gas during the increase and decrease of the O2 flow rate. The increase of the reactive gas flow without N2 in the gas mixture induces the formation of V2O5 on the target and collecting area. Because the sputtering yield of V2O5 is much lower than that of pure V, less metal will be deposited on the collecting area, and the chemisorption rate will decrease abruptly. Consequently, higher cathode voltage will be required to maintain the discharge and cause hysteresis. In addition, data from the target voltage as a function of the O2 flow rate indicate the vanishing hysteresis after the addition of N2 in the gas discharge. The experimental results in Fig. 2(b) confirm the numerical finding. After the addition of N2 in the gas mixture, both gases will start to compete for compound formation. The sputtering yield of the nitride layers is much lower than that of pure V, but is still greater than V2O5. Therefore, it is expected that the transition to the oxide mode becomes smoother after the addition of N2, because the nitrogen atoms contribute to avoiding instabilities in the transition region.
All of the compounds employed in the numerical model were confirmed by XPS. The XPS spectrum of film surface
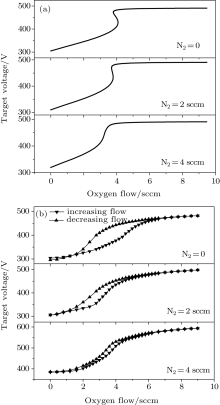 | Fig. 2. Numerical results (a) and experimental curves (b) of the target voltage as a function of the O2 flow rate at N2 flow of 0, 2, and 4 sccm. |
was fitted with mixed Lorentzian– Gaussian profiles after subtraction of a Shirley function using software XPSpeak4.1. The N1s core level for film deposited at O2 flow rate of 3.0 sccm, 3.2 sccm, 3.4 sccm, 3.8 sccm, and 5.0 sccm are shown in Figs. 3(a)– 3(e), respectively. According to the results, films deposited at low O2 flow rate are mainly composed by V– N, N– C, and N– O. Increasing the O2 flow rate, the fraction of VN is relatively reduced and the fraction of NO is gradually increased. At O2 flow rate of 3.4 sccm, O atoms diffuse in the VN lattice and replace N atoms, therefore removing the compound of VN. Consequently, the fraction of VN drops to zero. At high oxygen flow, the fraction of NO continues to increase and the film becomes mostly covered by N– O (see Figs. 3(c)– 3(e)).
The V2p3/2 core level, depicted in Fig. 4, was decomposed in four characteristic contributions: V0+ , V3+ , V4+ , and V5+ . These peaks are, respectively, assigned to V, V2O3, VO2, and V2O5.
When the oxygen flow is fairly low (spectrum (a)), all of the four-species states are found. As the O2 flow rate
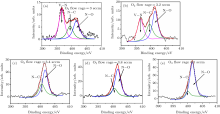 | Fig. 3. XPS spectra for N1s core levels for film deposited at O2 flow rates of (a) 3.0 sccm, (b) 3.2 sccm, (c) 3.4 sccm, (d) 3.8 sccm, and (e) 5.0 sccm. |
increases, the film is oxidized due to oxidation of VN and chemisorption of oxygen particles. With the increase in the oxygen flow (spectrum (b)), V0 gradually disappears due to the increased oxygen concentration. When oxygen flow is increased to around 4.2 sccm, the intensity of V3+ drops to negligible level. At very high oxygen flow (spectrum (d)), only V5+ is detected. From the XPS measurement analysis results shown in Figs. 3 and 4, it is also noted that the fraction of VN is quite lower than that of VOx, indicating that the incorporation of N element into the growing film is very small. This phenomenon will also be seen in Fig. 5(b).
 | Fig. 4. V 2p3/2 lines of vanadium oxides film taken at different samples with different oxygen flow. Oxygen flow is (a) 2 sccm, (b) 3.8 sccm, (c) 4.2 sccm, and (d) 6 sccm. |
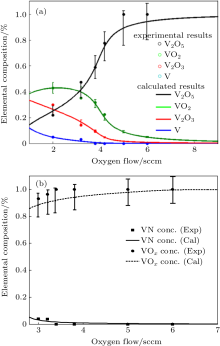
The film stoichiometry obtained from modeling and experiment is shown in Fig. 5(a). The nitrogen flow is kept constant at 4 sccm. The fraction of θ s4 increases with the increase of oxygen flow. In the region of oxygen flow up to 3.5 sccm, the fraction of θ s4 is higher than θ s3, and θ s1 almost reaches zero. Furthermore, with the continued increasing amount of oxygen, θ s4 increases asymptotically to one. Meanwhile, the fraction of metal V, V2O3, and VO2 is reduced and eventually disappears. There are several reasons for the shape of these curves. For a zero flow of oxygen the target is to some extent oxidized and the rest is metallic, while at higher flows of oxygen the target is essentially oxidized. After the 3.5 sccm point, the amount of O2 consumed to VO2 surpasses the amount of O2 gettered by deposited V and V2O3, resulting in a drastic increase in the fraction of θ s4. It should also be noted that the fraction of VO2 is generally higher than that of V2O3, which means that the films contain significantly more VO2 than V2O3. This is a consequence of the higher reactivity of V2O3 than V with oxygen.
Another interesting feature observed from the modeling result is that θ s1 and θ s3, corresponding to the fraction of metal vanadium and V2O3, decrease dramatically in the region from 3.0 to 4.0 sccm. However, the fraction of VO2 climbs down much slowly than V and V2O3 in the region from 3.0 to 4.0 sccm. This effect could be explained by the replacement reaction of VN by O2 atoms because of higher reactivity of O2 than N2, which decreases the fraction of VN and increases fraction of VO2.
These results show that the trends in the experiments are adequately described by the simulations. It is found that the error between experimental and modeling results is less than 15% over the whole figure, and is less than 8% for most values.
In order to study the effect of additional N2 on the film composition, a direct comparison between the experimental and modeling results of VN and VOx fractions as a function of oxygen flow rate is shown in Fig. 5(b). There appears to be a reasonable agreement between the numerical and experimental data. It is found that the error is less than 10% . Increasing the O2 flow rate, we observe a decrease in the VN concentration and an increase in the VOx content by XPS. According to Ref. [24], if the film stoichiometry is governed by oxidation processes, then a complete oxidation of the film surface is expected at high O2 flow rates once the formation of oxides is energetically more favorable than nitrides.
In this paper the reactive sputtering deposition of N-doped VOx has been studied both numerically and experimentally at different reactive gas mixtures. A kinetic model of reactive sputtering is proposed to modify Berg's model by taking into account the five species V, V2O3, VO2, V2O5, and VN in the N-doped vanadium oxides film. The fraction of compound on the substrate surface has been investigated as a function of reactive gas flow. From simulation results, substrate surface coverage is estimated.
Vanadium oxide films with nitrogen as an additional reactive gas have been deposited by reactive magnetron sputtering using different oxygen flow rates. Film compositions obtained from the XPS analysis are compared to the composition obtained from simulations and we reach a satisfactory agreement. Results show that the compound of VN is only found at very low O concentration because the replacement reaction of VN by O2 atoms owns higher oxygen flow rates and the incorporation of nitrogen into the growing film is quite small.
We also find that the smoother transition of the metallic mode to the oxide mode and the vanishing hysteresis after the addition of N2 are mainly attributed to the reduction of the sputtering yield and the decrease of the reactive gas consumption in the metallic mode.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|