Corresponding author. E-mail: llzhu@zju.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 11472243, 11302189, and 11321202), the Doctoral Fund of Ministry of Education of China (Grant No. 20130101120175), the Zhejiang Provincial Qianjiang Talent Program, China (Grant No. QJD1202012), and the Educational Commission of Zhejiang Province, China (Grant No. Y201223476).
We investigate the effects of pre-stress and surface tension on the electron–acoustic phonon scattering rate and the mobility of rectangular silicon nanowires. With the elastic theory and the interaction Hamiltonian for the deformation potential, which considers both the surface energy and the acoustoelastic effects, the phonon dispersion relation for a stressed nanowire under spatial confinement is derived. The subsequent analysis indicates that both surface tension and pre-stress can dramatically change the electron–acoustic phonon interaction. Under a negative (positive) surface tension and a tensile (compressive) pre-stress, the electron mobility is reduced (enhanced) due to the decrease (increase) of the phonon energy as well as the deformation-potential scattering rate. This study suggests an alternative approach based on the strain engineering to tune the speed and the drive current of low-dimensional electronic devices.
Low-dimensional structures such as silicon nanowires have stimulated considerable interest due to their potential applications in nanoelectronic or nanomechanical devices.[1, 2] These nanostructures display unique and enhanced mechanical, electric, and thermal properties with respect to the corresponding bulk materials. The tiny sizes endow these nanostructures with novel physical and mechanical properties, which demands a better understanding. The phonon properties which are relevant to the thermal and electric performance in semiconductor nanostructures, have attracted much scientific attention.[3– 7] Through controlling and manipulating the phonon dispersion, the phonon group velocity, and the density of states, the phonon engineering approaches have been suggested to tune the thermal and electric properties of the nanostructures, for example, the phonon thermal conductivity and the electron– acoustic phonon interaction.[7– 10]
The electron– acoustic phonon interaction is of high interest since it inevitably influences the charge carrier mobility in the semiconductor nanostructures, which is linked to the performance of complementary metal– oxide– semiconductors (CMOS). A higher mobility would lead to a shorter switching time and a lower power consumption. The carrier mobility is also related to the performance of the thermoelectric materials, and increasing the mobility[11– 13] can improve the thermoelectric figure of merit. For instance, Fujisawa et al.[11] demonstrated the importance of the electron– acoustic phonon interaction in the spontaneous emission spectrum of double quantum dot devices for non-suspended quantum dots in AlGaAs/GaAs heterostructures; Wang et al.[12] highlighted the contribution of the electron– phonon coupling in achieving a good thermoelectric performance in n-type PbSe. On the other hand, the phonon engineering approaches have been widely applied to tune the electron– acoustic phonon interaction by tailoring the phonon mode spectrum, [10] including the spatial confinement, [14, 15] variations in the geometrical sizes of the nanostructures, [16, 17] and a proper selection of acoustically mismatched nanostructures.[18, 19]
Considerably large residual stresses exist in the layered nanostructures as well as in the nanoelectronic devices, [20, 21] these pre-stresses lead to significant changes in the acoustic phonon properties, though the acoustoelastic effect due to the stresses can be negligible in the bulk materials. In addition, the surface tension, which arises from the dynamic structural changes of the surface atoms or the redistributed charge density on the surface, [22] can also influence the phonon performance of the nanostructures. Many studies have been devoted to understanding how the imposed strain/stress fields and the surface tension influence the mechanical and physical properties, such as the elastic modulus, thermal and electric properties, in the bulk materials and the nanostructures.[22– 30] For example, Osetrov et al.[31] studied the acoustoelastic effect in layered heterostructures and concluded that the acoustic wave propagation could be severely affected by the residual stress as well as the third-order elastic constants; Zhu and Zheng[32] applied the continuum elastic theory to simulate the phonon properties and showed that the stress field can modify the phonon thermal conductivity of a nano film completely; Liangruksa and Puri[25] revealed that the lattice thermal conductivity can be changed by the surface tension in silicon nanowires. However, only a few of studies have been undertaken to provide insights into the electron– acoustic phonon interaction in the stressed nanostructure.[8] In this work, we investigate the electron– acoustic phonon interaction and the mobility in silicon nanowires under both pre-stress and surface tension. The continuum elastic theory is utilized to calculate the phonon properties with spatial confinement and acoustoelastic effect in the rectangular nanowires. Through taking into account the surface energy, the effect of the surface tension is absorbed into the effective elastic modulus of the nanowires. The interaction Hamiltonian for the deformation potential associated with confined acoustic phonons in the stressed nanowires is formulated to obtain the electron– acoustic phonon scattering rate and the mobility. The quantitative results are presented to illuminate the effects of the surface tension and the pre-stress on the phonon dispersion, as well as the resulting electron– acoustic phonon coupling in the silicon rectangular nanowires. It is found that the scattering rate and the mobility are sensitive to the surface tension and the pre-stress.
The continuum elasticity theory is generally utilized to characterize the acoustic phonon properties of spatially confined nanostructures.[33, 34] The wave equation of the displacement field for elastic vibrations in an anisotropic structure can be given as
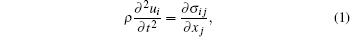 |
where ρ is the density of the natural state, u(u1, u2, u3) is the displacement vector, and σ ij = Cijklukl is the stress tensor with Cijkl being the natural second-order elastic modulus tensor. When the size of a structure shrinks to the nanometer scale, the surface plays a central role in the performance of the nanostructure. In the presence of the surface tension the surface strain energy needs to be accounted for in deriving the elastic properties of the nanowire, which can be expressed as
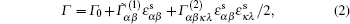 |
where 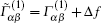

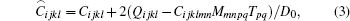 |
where 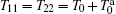



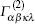

It is worth noting that the normal acoustic vibration modes in free-standing rods of rectangular cross-section have been studied by Morse in homogeneous and isotropic approximation.[40] When the thermal energy or the acoustic wave propagates along the x3 direction, the displacements of the nanowire are functions of x1, x2, and x3, and one can look for the solution of Eq. (1) in the form of u = û (x1, x2)exp [i(q0 · x3 − ω t)], where q0 is the wave vector and ω is the phonon frequency. The boundary conditions of the nanowire are taken as
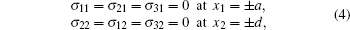 |
where 2a is the thickness and 2d is the width. By adopting the approximate separation of variables solution given by Morse for the compressional modes, the dispersion relation of the thickness modes is given by
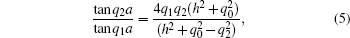 |
which results from the conditions to determine the coefficients in the displacement solutions. We have
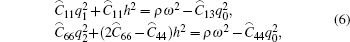 |
where 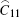
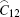
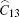
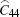

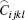
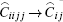
Consider a silicon nanowire subjected to a lateral stress, which is equal in both transverse directions, as shown in Fig. 1. Suppose the nanowire is isotropic, the initial stress state of the nanowire is given by 

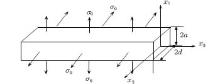 | Fig. 1. Schematic diagram of a stressed rectangular silicon nanowire with pre-stress σ 0 in x1 and x2 directions. |
 |
where 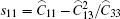



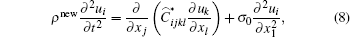 |
where ui is the displacement vector, ρ new ≈ ρ (1 – Δ u0) is the density with the static strains, and 

 |
The non-zero components of the effective elastic modulus can be written explicitly as
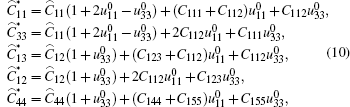 |
and 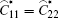
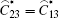
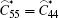

 |
Then, the phonon dispersion relation in the stressed nanowire under the applied surface stress can be determined through combining Eqs. (5) and (11).
The electron– acoustic phonon interaction includes the contributions from both the deformation potential coupling and the piezoelectric coupling. Since the focus of this work is on the variations of the deformation potential in the stressed silicon nanowires with surface tension, the latter contribution will be ignored in the following discussion. The Hamiltonian for the electron– acoustic phonon interaction through the deformation potential coupling of the thickness mode in the rectangular nanowire is written as
 |
where cn, m (q0) and 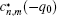
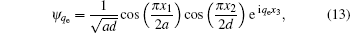 |
with the eigenenergy
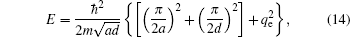 |
where qe is the wave vector of the electrons. The relevant electron– phonon matrix element is
 |
Here, A is the constant related to the size of the wire and parameters q1 and q2. According to Fermi’ s golden rule, the electron– acoustic phonon scattering rate corresponding to the matrix element in Eq. (15) can be obtained as
 |
where 
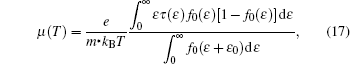 |
where f0 is the Fermi distribution, e is the electron charge, m* is the effective electron mass, and ε 0 is the electron ground-state energy. Note that the strain/stress fields can alter the effective masses, the number of conduction channels, and the deformation potentials, all of which can influence the mobility of the silicon nanowires.[42– 44] Since our goal is to focus on the modification of the carrier mobility stemming from the change of the phonon dispersion by the stress fields, the contribution of the electronic structures in the stressed nanowires is not taken into account.
To demonstrate how the stress fields, including the applied surface tension and the pre-stresses, affect the phonon properties and the relevant electron– acoustic phonon interaction in the confined silicon nanowires, numerical calculations are conducted. The bulk elastic parameters of silicon, Cijkl and Cijklmn, are given in Ref. [45]. As an example, we present the phonon energy as a function of the phonon wave vector, corresponding to the thickness mode, under different stress states. Firstly, the phonon dispersion relation with a positive or negative applied surface stress in a 6 nm× 12 nm free-standing nanowire is shown in Fig. 2. Our results clearly indicate that the dispersion relation is sensitive to the surface stress. A negative surface tension reduces the phonon energy while a positive one increases it. With increasing wave vector q, the phonon energy changes more and more significantly under the surface tension. One can also note that a negative surface stress affects the phonon properties more significantly than a positive one does. Next, the phonon energy of the silicon nanowire under different pre-stresses as a function of the phonon wave vector is shown in Fig. 3. One can see from Fig. 3 that a compressive stress leads to an increase in the phonon energy, whereas a tensile stress reduces the phonon energy, which is of an inverse trend to the variation of the phonon energy induced by the surface tension. Meanwhile, unlike the case of the silicon nanowire under an applied surface tension, the tensile pre-stress has more contributions to the phonon energy than the compressive one does. Figures 2(b) and 3(b) plot the phonon dispersion relations of a silicon nanowire with a cross-section of 12 nm× 24 nm under different stress states. The calculations suggest that the influences of the surface tension and the pre-stress on the phonon energy are associated with the size of the wire. The thicker nanowire has less variation of the phonon energy under both applied surface tension and pre-stresses.
The electron– acoustic phonon scattering rates originated from the deformation potential interaction have been calculated for the silicon nanowire, where the aspect ratio of width to thickness is taken as two. The scattering rates for emission and absorption under different stresses are displayed as functions of the electron energy in Figs. 4(a) and 4(b) for the silicon nanowire with the cross-section of 6 nm× 12 nm. A distinct and important feature shown in Fig. 4 is that, for the scattering rate of emission at low energies, a negative surface tension and a tensile pre-stress give rise to the pronounced peaks early, while a positive surface stress and a compressive pre-stress delay the appearance of the peaks. It is also interesting to note in Fig. 4(a) that under a positive (negative) surface tension, the scattering rate is enhanced (reduced) on the left hand side of the peak while the rate is decreased (increased) on the right hand side of the peak. However, with the presence of the pre-stresses, the scattering rate of emission remains enhanced (weakened) under the tensile (compressive) pre-stress, which is independent on the appearance of the peaks, as shown in Fig. 4(b). For the case of absorption, a negative surface stress and a compressive pre-stress can both increase the scattering rate, and a positive surface tension and a tensile pre-stress make the rate decreased. Figure 5 presents the calculations analogous to those of Fig. 4 for the nanowire with the cross-section of 12 nm× 24 nm. One can notice from Figs. 4 and 5 that the contributions of the applied surface stresses and the pre-stresses to the scattering rate of the silicon nanowire are sensitive to the thickness of the wire. The imposed stresses can affect the electron– acoustic phonon interaction more significantly for the smaller wire. This can be understood by the fact that the spatial confinement of the phonon becomes more remarkable with the decreased diameter of the nanowire. Furthermore, it can be noted from Figs. 4(a) and 4(b) that the scattering rate of emission is much more sensitive to the applied surface than the rate of absorption.
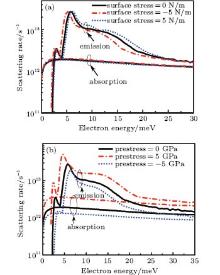 | Fig. 4. Deformation-potential scattering rates for silicon nanowire with (a) different applied surface stresses and (b) different pre-stress fields. The cross-section of the wire is 6 nm× 12 nm. |
 | Fig. 5. Deformation-potential scattering rates for silicon nanowire with (a) different applied surface stresses and (b) different pre-stress fields. The cross-section of the wire is 12 nm× 24 nm. |
The dependences of the phonon dispersion and the electron– acoustic phonon interaction on the applied surface tension and the pre-stresses lead us to believe that an imposed stress field can also alter the carrier mobility of the silicon nanowire. Indeed, the total carrier mobility of the silicon nanowire can be calculated by summing its values corresponding to the scattering rates for absorption and emission. Figure 6(a) plots the temperature dependent mobility of the Si nanowire with different surface tensions, in which the thickness and the width modes of phonons are both included in the scattering rates. Clearly, the applied surface tension changes the dependence of the mobility on temperature significantly. Similar to the phonon dispersion, a positive surface tension is found to enhance the mobility while a negative surface tension suppresses the carrier moving capability of the wire. In addition, the mobility as a function of the temperature is also shown for various pre-stresses in Fig. 6(b). Through comparison with the results in Fig. 6(a), it is noteworthy to point out that the decrease in the mobility caused by the negative surface tension and the tensile pre-stress is much greater than the increase in the mobility originating from the positive surface tension and the compressive pre-stress. The most striking feature revealed in Figs. 6(a) and 6(b) is that the appearance of a positive surface stress and a compressive pre-stress makes the mobility a bit more sensitive to the temperature, whereas a negative surface tension and an extensional pre-stress tend to significantly minimize any temperature dependence of the carrier mobility. Finally, we present the comparison between the predicted change of the electron mobility in the stressed silicon nanowire with that in the stressed bulk silicon[46, 47] in Fig. 7(a). It can be noted that the slope of the curve for the silicon nanowire in the range of stress less than 500 MPa is quite different from that for the bulk silicon, while the saturation value of the change of mobility in the nanowire for the compression stress is close to the value in the bulk case. In addition, we also plot the electron mobility as a function of the pre-strain in Fig. 7(b) and make a comparison with the results simulated by an atomic method for the 〈 001〉 silicon nanowire. It is clearly noted that the predicted strain-dependent mobility is agreeable with the one obtained from the atomic simulations.[44]
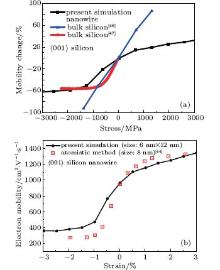 | Fig. 7. (a) Comparison of the change of carrier mobility with the stress field between the silicon nanowire of cross-section 6 nm× 12 nm and the bulk silicon.[46, 47] (b) The predicted electron mobility varied with the strain based on the present calculations compared with that from the atomistic simulations for 〈 001〉 nanowires.[44] |
We have explored the electron– acoustic phonon interaction and the carrier mobility of the stressed silicon nanowires under applied surface tension. The effects of the surface tension and the pre-stress on the phonon dispersion and the deformation potential induced electron– acoustic phonon scattering rate of the wire are quantitatively studied. The numerical results indicate that the surface stress and the pre-stress field can significantly modify the phonon performance, such as the phonon dispersion and the electron– acoustic phonon interaction, which ultimately affect the carrier mobility of the nanowire. In addition, we also show that the stress can adjust the sensitivity of the electron– acoustic phonon scattering rate and the mobility to the physical size of the wire as well as to the temperature. These results may shed light on an alternative and efficient approach for controlling the phonon properties and enhancing the performance of various nanoelectronic devices.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|




