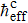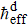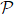† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11864014 and 11804130).
We investigate the quantum to classical transition induced by two-particle interaction via a system of periodically kicked particles. The classical dynamics of particle 1 is almost unaffected in condition that its mass is much larger than that of particle 2. Interestingly, such classically weak influence leads to the quantum to classical transition of the dynamical behavior of particle 1. Namely, the quantum diffusion of this particle undergoes the transition from dynamical localization to the classically chaotic diffusion with the decrease of the effective Planck constant ℏeff. The behind physics is due to the growth of entanglement in the system. The classically very weak interaction leads to the exponential decay of purity in condition that the classical dynamics of external degrees freedom is strongly chaotic.
Rich dynamical behavior in periodically-driven systems has attracted extensive attention in recent years.[1–3] It is found that periodical driving induces quantized transport,[4,5] topological phase transition,[6–8] and thermalization of quantum dynamics,[9,10] just to name a few. Among these, the quantum transport in momentum space is particularly important, as it provides an insight on the mapping of transport phenomenon from position to momentum space. As an example, the dynamical localization (DL) in momentum space[11–13] is an analog of the Anderson localization in position space,[14] both of which result from the disordered feature of the system.[15] Nowadays, the transport phenomenon in momentum-space lattice has been a fruitful subject in physics, where the intriguing phenomena, such as topologically-protected quantum walk[16] and exponentially-fast diffusion[17–21] have been reported.
Theoretical investigations have stimulated experimental studies on the transport phenomenon in periodically-driven quantum systems. Recently, the DL was observed in the atom-optics experiments on the periodically-driven ultracold atoms[22] and molecules.[23] Even more remarkable, experimental advances in atom-optics have made it possible to actively tune the driven laser to be a quasiperiodic[24–26] or random sequence,[27] and thus to investigate the diffusion behavior in a controlled manner, e.g., the Anderson transition for the quasiperiodical kicking systems, and the decoherence-induced subdiffusion for the random kicking systems. These investigations greatly broaden our understanding on the exotic transport phenomenon induced by quantum coherence.[28–30]
It is known that the unavoidable coupling between system and environment destroys quantum coherence,[31] and consequently leads to the appearance of the classically chaotic diffusion from the underlying quantum dynamics.[32–41] Interestingly, the influence from a single chaotic particle can effectively produce the decoherence effects.[42–46] The quantum–classical correspondence (QCC) which is induced by the interaction with a few degrees of freedom[47–50] has been recently observed in a ultracold atoms experiment.[51] In the past decades, the influence of interatomic interactions on the quantum diffusion has received considerable investigations.[52–54] Rich diffusion behaviors, such as subdiffusion[55–61] and exponentially-fast diffusion,[18,19,21] have been observed. This topic regains attention as it is closely associated with the issue of dynamical many-body localization,[62–65] since the system of coupled periodically-kicking particles is an ideal system to explore the diffusion behavior in discrete momentum-space lattice.[66–69] At present, the fate of dynamical many-body localization under the interaction of particles is still an open question.[70]
Motivated by these studies, we investigate the quantum diffusion in a system involving two-coupled particles. The system is periodically driven by impulsive fields. We concentrate on both the classical and quantum dynamics of one particle (say particle 1) under the interaction with the other one (say particle 2). Interestingly, the effects of particle 2 with mass m on the classical diffusion of particle 1 with unity mass decrease as m decreases, and it is negligibly small when m ≪ 1. The reason is that particle 2 of very small mass possesses little energy to affect the classical motion of particle 1. More importantly, the classically vanishing small influence is able to destroy the DL of particle 1. It even leads to the appearance of classically chaotic diffusion in quantum dynamics when the effective Planck constant ℏeff is small enough. To characterize the quantum entanglement, we numerically investigate the purity of the quantum state. The issue we address here is the sensitivity of entanglement to the classical chaoticity of the external degrees of freedom. We find that the time dependence of purity exhibits the power law decay for the regular motion of the classical dynamics of particle 2, and the exponential decay for the chaotic motion.
The paper is organized as follows. In Section
We consider two interacting particles which are trapped in an infinitely square well and periodically kicked by optical lattices. The Hamiltonian reads
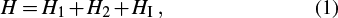


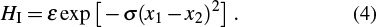
It is useful to introduce a set of scaled dimensionless units. Time is scaled by T, i.e., t′ = t/T, which means that t′ denotes the number of kicks. The canonical coordinate and momentum variables are redefined as 


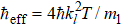
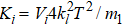

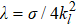





We concentrate on both the classical and quantum dynamics of particle 1. Numerically, we use the split-operator method to simulate the time evolution of the quantum dynamics. The initial state is a product state of the ground state of each particle, i.e., ψ(0) = ϕ1(0)ϕ2(0) with 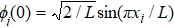
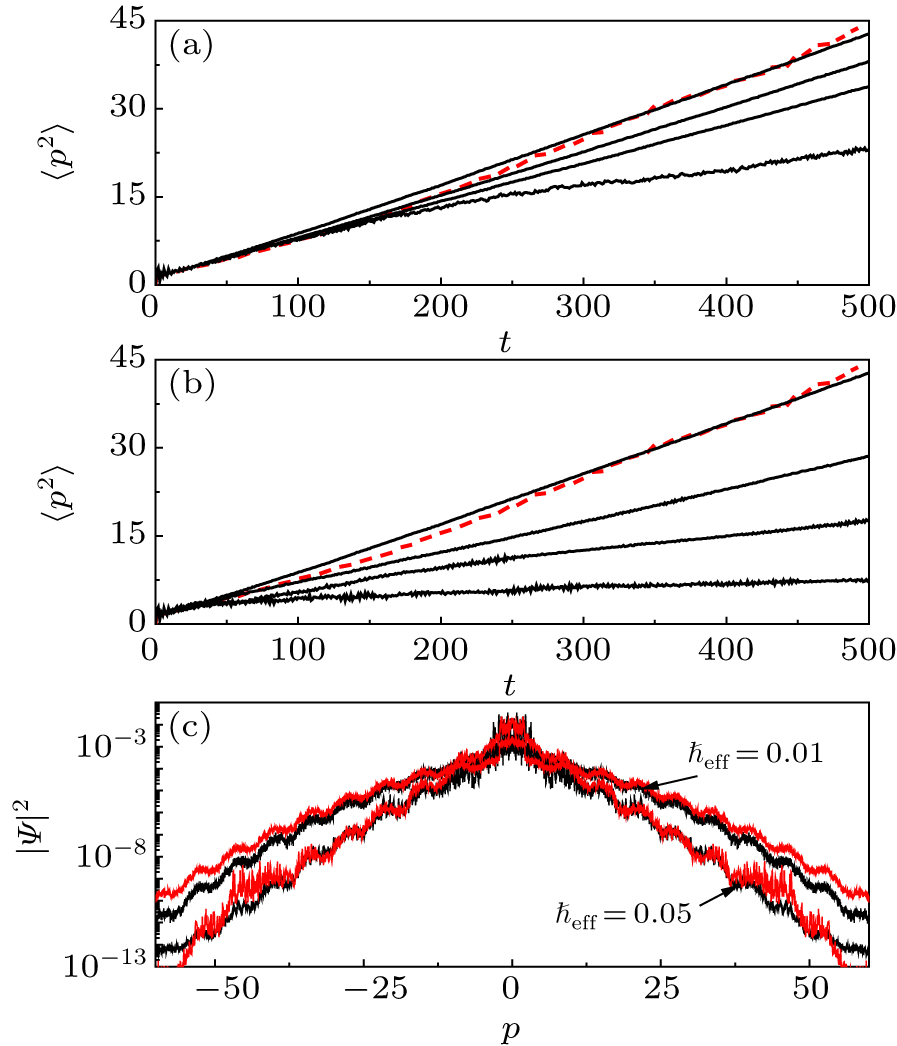
The typical character of classically chaotic diffusion is the linear growth of the mean energy with time, i.e., 〈 p2(t) 〉c = Dc t, where 〈 ⋅ 〉c stands for the ensemble average over many trajectories and Dc is usually termed as the classical diffusion coefficient (CDC).[71–74] This phenomenon is traditionally referred as normal diffusion. Our numerical investigations show that the mean energy of particle 1 linearly increases with time 
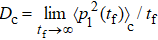
We numerically investigate the quantum diffusion of particle 1 when its classical counterpart is almost unaffected which is ensured by the condition m ≪ 1. The quantum mean energy 
In chaotic situation, the motion of particle 2 of very small mass behaves like random noise. It is known that external noises can destroy quantum interference and thus leads to the classically chaotic diffusion.[75–77] As a further step, we consider the case that the kick strength contains random noises, for which the Hamiltonian reads


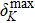





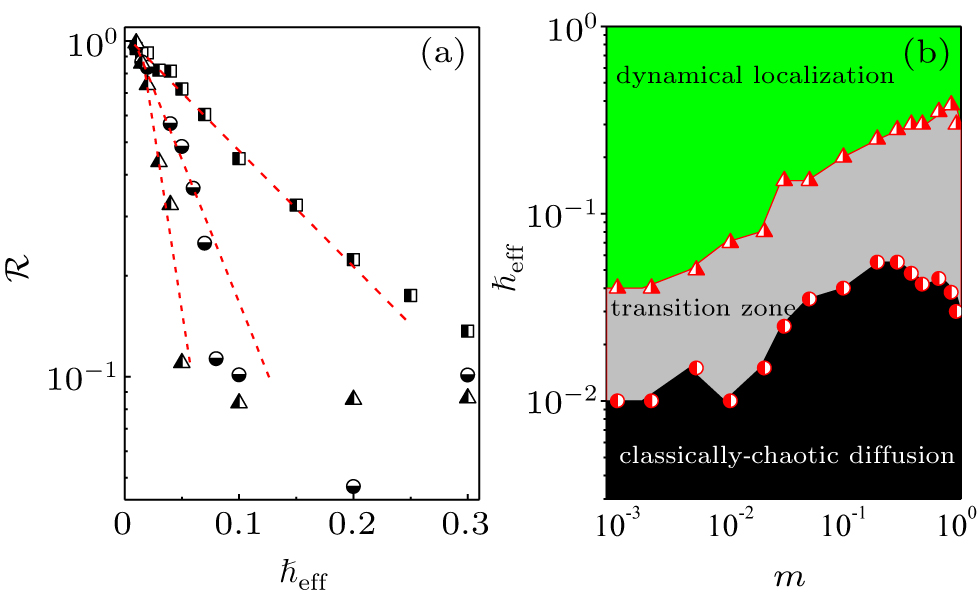
We quantify the difference between quantum and diffusion coefficients of particle 1 by using the ratio ℛ = Dq/Dc, where the quantum diffusion coefficient is defined as 
Furthermore, we define the criteria of the appearance of the classically chaotic diffusion and DL as ℛ = 0.9 and 0.1, respectively. We numerically obtain the threshold values of ℏeff corresponding to ℛ = 0.9 and 0.1, which are separately termed as 


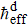
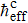

A commonly used measure of quantum entanglement is purity 
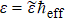
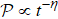

We numerically investigate the entanglement involving a few degrees of freedom via two coupled particles. We show that, the effect of particle 2 on the classical behavior of particle 1 decreases as its mass (m) decreases. Under the classically weak perturbation (m ≪ 1), the quantum diffusion behavior of particle 1 undergoes a transition from DL to chaotic diffusion with the decrease of ℏeff. We numerically investigate the difference between quantum and classical diffusions for a wide regime of ℏeff and m, and find the exponential decay of ℛ with ℏeff. By using this quantity, we define the boundary for the appearance of DL and classically-chaotic diffusion. Numerically, we obtain a “phase” diagram of the quantum diffusion in the parameters space (ℏeff, m). The quantum to classical transition is accompanied by the growth of entanglement. For the vanishingly small interaction ε ∝ ℏ with ℏeff ≪ 1, the time decay of purity is exponentially fast in condition that the classical dynamics of particle 2 is strongly chaotic. Such exponentially-fast entanglement is stable in the sense that the time dependence of purity is almost unchanged as K2 varies. Our investigation has important implication for the fundamental problem of the quantum to classical transition.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] |