In 2008, Fu and Kane proposed that the superconducting proximity effect between an s-wave superconductor (S) and the surface of a three-dimensional (3D) topological insulator (TI) can induce p-wave-like superconductivity and host Majorana bound states (MBSs) in the vortex cores or in the proximity-type S–TI–S Josephson trijunctions.^[1] In more detail, the electron-like and hole-like Andreev bound states (ABSs) in single S–TI–S Josephson junctions are predicted to have 4π-period energy phase relations (EPRs), and the 1D Majorana edge modes are predicted to be fully decoupled when the phase difference reaches π, resulting in the complete close of minigap between the electron-like and hole-like ABSs. In Josephson trijunctions on 3D TIs, furthermore, MBS is predicted to exist at the center of the trijunction over extended regions in phase space. In the last years, experimental efforts have been paid to search for 4π-period current phase relations (CPRs), which are direct consequences of 4π-period EPRs. Some signatures, such as skewed CPR,^[2–4] missing of odd Shapiro steps,^[5–8] etc., have been discovered. Meanwhile, a contact-resistance-measurement method has also been developed for directly probing the EPRs in the junction area.^[9–11] A linear closing behavior of minigap as a signature of 4π-period EPRs in single S-TI-S junctions and the complete close of minigap at the center of the S–TI–S trijunctions as an evidence of MBS have been observed.^[10,11]

To further study the fractional Josephson effect in which the missing of odd Shapiro steps^[5–8] is regarded as a signature of MBS, one would require to perform the contact-resistance-measurement method in the presence of radio-frequency (rf) irradiation in order to obtain the information of EPR and MBS. More generally, since MBSs suffer poisoning from quasiparticle fluctuations, one would ultimately require fast braiding/fusion operations and fast readout of MBSs at μs or ns time scales in the future, in order to test their non-Abelian statistics and to perform quantum computation. However, at such a short time scale and in the radio/micro frequency range, it is unclear whether the contact-resistance-measurement method can still be applied to probe the minigap, hence the MBSs, in the S–TI–S junctions. To clarify this issue, in this work we investigate the contact-resistance-measurement method in the presence of rf irradiation. We find that this method still works — the measured data of contact resistance under rf irradiation can be well understood and numerically simulated by using the resistively shunted Josephson junction (RSJ) model^[12] and the Blonder–Tinkham–Klapwijk (BTK) theory.^[13]

Figure 1(a) shows the false-color scanning electron microscopy (SEM) image of the device. The two superconducting Al electrodes couple with each other through a Bi₂Te₃ flake (∼100 nm thick) to form a Josephson junction of length L ∼ 153 nm and width W ∼ 484 nm. The surfaces of the Al electrodes were oxidized in situ after deposition. An additional insulating layer of overexposed polymethyl methacrylate (PMMA) was fabricated to cover the device except for a window at the junction area (marked by the dashed rectangle in Fig. 1(a)). Through this window, a normal-metal Pd electrode was further deposited to electrically contact with the TI surface in the junction area for contact resistance measurement. Figure 1(b) shows the schematics of the device, together with the configurations for measurements of Josephson supercurrent (blue circuits) and contact resistance (yellow circuits). The measurements were carried out in a dilution refrigerator with a base temperature of ∼ 10 mK. The rf irradiation was applied via a coaxial cable with an open end as an antenna near the device.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. Device structure and measurement configuration. (a) False-color SEM image of the proximity-type Josephson junction. A Josephson junction with Al electrodes (blue) was fabricated on the surface of a Bi2Te3 flake (gray, the whole image). The normal-metal Pd electrode (yellow) was deposited to contact the junction area through a window (marked by the dashed rectangle) on the insulating mask made of overexposed PMMA. Note that the surfaces of the Al electrodes were oxidized in situ before evaporating Pd. (b) Schematics of the device under rf irradiation. The configurations for measurements of contact resistance (yellow) and for Josephson supercurrent (blue) are illustrated.

In the following, we will first present and discuss the I_J–V_J curves (where I_J is the current passing from one superconducting electrode to another, and V_J is the voltage drop across the Josephson junction), and then present and discuss the data of contact resistance between the Pd electrode and Bi₂Te₃ under rf irradiation.

In the presence of rf irradiation, it is known that there will be Shapiro steps on the I_J–V_J curves of a Josephson junction.^[12] Figure 2(a) shows the measured differential resistance dV_J/dI_J as a function of I_J and rf power P_rf applied to the antenna. Figure 2(b) shows the same data as in Fig. 2(a), but converted and replotted as a function of V_J and P_rf. The horizontal lines correspond to well defined Shapiro steps in the I_J–V_J curves at voltages V_Jn = nhf_rf/2e = n × 1.04 μV, where h is the Planck constant, f_rf = 0.5 GHz is the rf frequency, e is the electron charge, and n = 0, ± 1, ± 2, …

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Shapiro maps in an Al–Bi2Te3–Al junction. (a) Differential resistance dVJ/dIJ as a function of rf power Prf and direct bias current IJ, measured at rf frequency frf = 0.5 GHz. (b) The same data as in (a), but replotted as a function of rf power Prf and direct voltage VJ across the junction in units of hfrf/2e. Evenly spaced Shapiro steps can be seen. (c) Simulated dVJ/dIJ based on the RSJ model. (d) The same simulated dVJ/dIJ as shown in (c), but in a wider range of rf power. The black line represents the critical supercurrent Ic, and the red curve represents the sum of the critical supercurrent Ic and the amplitude of the rf-driving current Irf0.

Usually, the Josephson supercurrent has a 2π-period CPR, which leads to the appearance of ordinary Shapiro steps on the I_J–V_J curves in the presence of rf irradiation. If the supercurrent contains a 4π-period component, however, the odd Shapiro steps might disappear, leading to the so called fractional Josephson effect.^[14] In some S–TI–S junctions, the missing of the odd Shapiro steps has been observed.^[5–7] In our devices, however, figure 2(b) shows that all the Shapiro steps are present. It indicates that the dominant supercurrent in our devices has a 2π-period CPR, flowing presumably through the bulk of the Bi₂Te₃ flake,^[10] and that the 4π-period component of supercurrent in our device is negligibly small.

The I_J–V_J curves under rf irradiation can be simulated by solving the following equation based on the RSJ model:^[12]

With increasing rf power, the region containing Shapiro steps in Fig. 2 extends to higher currents/voltages. The border of this region roughly coincides with the red dashed curve in Fig. 2(d) which represents the sum of the critical supercurrent I_c (the black line) and the amplitude of the rf-driving current I_rf0. It reflects that the Josephson junction can still have the chance to mode-lock with the rf driving frequency (i.e., forming the Shapiro steps), as long as the total bias current I_J + I_rf0 sin (2πf_rft) has the chance to be smaller than the critical supercurrent I_c within each oscillation period.^[14]

In the next, let us present and discuss the data of the contact resistance dV_b/dI_b across the Pd–Bi₂Te₃ interface. Figure 3(a) shows the dV_b/dI_b as a function of rf power P_rf and bias current I_b. The vertical line cuts in Fig. 3(a) at low rf powers take basically the same line shape as the red curve (P_rf = 0) shown in Fig. 3(b), with a superconductivity-related dip–peak–dip structure due to the existence of a minigap on the TI surface of the S–TI–S junction.^[10] Such a line shape can be well understood within the framework of the BTK theory.^[10,13] The black curve in Fig. 3(b) is the BTK fitting to the experimental data, with fitting parameters as follows: the minigap Δ₀ = 20.4 μeV, the effective number of channels of the contact N = 25.5, the barrier strength Z = 0.66, and the effective electron temperature T = 0.1 K. The standard error between the measured dV_b/dI_b (black) and the fitting curve (red) in Fig. 3(b) , where M = 501 is the number of data points in Fig. 3(b), y_mi and y_fi are the measured and the fitted dV_b/dI_b at I_b of index i, respectively. The relative standard error is ∼ 25.7 Ω/720 Ω = 3.6%.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Differential contact resistance in the junction. (a) The differential contact resistance dVb/dIb across the Pd–Bi2Te3 interface as a function of rf power Prf and bias current Ib. (b) The dVb/dIb as a function of bias current Ib in the absence of rf irradiation (red curve), together with the BTK fitting (black curve). (c) The dVb/dIb calculated from the RSJ model and the BTK theory. The black line represents a characteristic current Ie at zero rf power, beyond which the signature of superconductivity disappears. The red dashed line represents the sum of Ie and the amplitude of the rf driving alternating current across the Pd–Bi2Te3 interface. (d) The rf power dependence of the measured dVb/dIb–Ib curves (red, from −36 dBm to −16 dBm) and the simulated ones (black) (curves are shifted vertically for clarity).

With increasing rf power P_rf, the dip–peak–dip structure on the vertical line cuts of Fig. 3(a), shown as the red curves in Fig. 3(d), gradually rounds up and spreads to higher I_b. The characteristic width of this structure, as indicated by the red dashed line in Fig. 3(c), follows a similar trace as the outer border of the Shapiro step regions in Fig. 2(a).

Theoretically, shining the device with rf irradiation will cause two effects on the contact resistance measurement. First, it will generate a rf current I_rf0sin(2πf_rft) flowing mainly through the bulk of the junction, by which influencing the time-dependent phase difference ϕ(t) of the Josephson junction, thus influencing the minigap Δ(t). Second, the rf irradiation will also generate a rf current passing through the Pd–Bi₂Te₃ interface, by which modifying the contact resistance measurement. Combining these two effects, the contact resistance can be simulated as follows, still by using the RSJ model and the BTK theory.

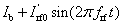
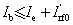
In the presence of rf irradiation, the time-dependent minigap of the surface state should follow the 4π -period form^[10] and can be expressed as Δ(t) = Δ₀|cos(ϕ(t)/2)|, where the time-dependent phase difference ϕ(t) can be obtained by solving Eq. (1). On the other hand, the time-dependent total bias current passing through the Pd–Bi₂Te₃ interface is , where I_b is the direct bias current and is the amplitude of the rf driving current (we set in order to fit the experimental data). We can extract the instant value of dV_b(t)/dI_b(t) by using the fitting parameters Δ₀, N, Z, and T obtained before. Then, the time average of dV_b(t)/dI_b(t), dV_b/dI_b, can be numerically obtained. The details of the simulation can be found in the supplementary materials. The simulated results are plotted in Fig. 3(c) and also as the black curves in Fig. 3(d) at several different rf powers. The red dashed line in Fig. 3(c) represents the border of , where I_e is a characteristic current beyond which there is no signature of superconductivity without rf irradiation. It can be seen that the rf driving current makes the measured minigap structure extend to higher bias current under rf irradiation. Nevertheless, the numerical simulations can still reproduce the measured data.

To conclude, we have examined and confirmed the validity of the contact-resistance-measurement method for detecting the minigap in S–TI–S Josephson junction under rf irradiation. Although both the phase difference across the Al–Bi₂Te₃–Al junction and the minigap measurement process across the Pd–Bi₂Te₃ interface are influenced by the rf irradiation, the measured contact resistance can still be interpreted by using the RSJ model and the BTK theory. These results might be useful when using the contact-resistance-measurement method to study the minigap of S–TI–S junctions under rf irradiation and Majorana-related physics.