Cite this Article
Ye Ming, Feng Peng, Wang Dan, Song Bai-Peng, He Yong-Ning, Cui Wan-Zhao. Secondary electron yield suppression using millimeter-scale pillar array and explanation of the abnormal yield–energy curve. Chinese Physics B, 2019, 28(7): 077901  
Permissions
Secondary electron yield suppression using millimeter-scale pillar array and explanation of the abnormal yield–energy curve
Ye Ming1, 2, †, Feng Peng1, Wang Dan1, Song Bai-Peng3, He Yong-Ning1, ‡, Cui Wan-Zhao4
School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China
Key Laboratory for Physical Electronics and Devices of the Ministry of Education, School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China
State Key Laboratory of Electrical Insulation and Power Equipment, School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China
National Key Laboratory of Science and Technology on Space Microwave, China Academy of Space Technology, Xi’an 710100, China

 

† Corresponding author. E-mail: yeming057@xjtu.edu.cn yongning@xjtu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. U1832190, 61501364, U1537211, and 11705142).

Abstract

The phenomenon of secondary electron emission is of considerable interest in areas such as particle accelerators and on-board radio frequency (RF) components. Total secondary electron yield (TSEY) is a parameter that is frequently used to describe the secondary electron emission capability of a material. It has been widely recognized that the TSEY vs. primary electron energy curve has a single-hump shape. However, the TSEY–energy curve with a double-hump shape was also observed experimentally—this anomaly still lacks explanation. In this work, we explain this anomaly with the help of a millimetre-scale (mm-scale) silver pillar array fabricated by three-dimensional (3D) printing technology. The TSEY–energy curve of this pillar array as well as its flat counterpart is obtained using sample current method. The measurement results show that for the considered primary electron energy (40–1500 eV), the pillar array can obviously suppress TSEY, and its TSEY–energy curve has an obvious double-hump shape. Through Monte Carlo simulations and electron beam spot size measurements, we successfully attribute the double-hump effect to the dependence of electron beam spot size on the primary electron energy. The observations of this work may be of help in determining the TSEY of roughened surface with characteristic surface structures comparable to electron beam spot size. It also experimentally confirms the TSEY suppression effect of pillar arrays.

PACS: 79.20.Hx;29.20.-c
Keyword:secondary electron emission;pillar array;total secondary electron yield suppression
1. Introduction

Secondary electron emission is of particular interest to various applications, including but not limited to accelerator,[1,2] high power microwave components on satellite,[3,4] and electric propulsion.[5] Total secondary electron yield (TSEY), which is frequently used to characterize the secondary electron emission capability of a material, refers to the average emitted electrons per incident primary electron. Generally speaking, TSEY is determined by the outermost surface of the target material. When primary electron energy is no more than a number of keV, the thickness of surface layer responsible for secondary electron emission is just a number of nanometers. For applications such as electron cloud suppression of particle accelerators, TSEY suppression is favored. Various surface treatment methods have been studied for this purpose, such as carbon coating,[6] TiN coating,[7] plasma bombardment,[8] vacuum pyrolyzing,[9] and surface roughening.[10–18] For example, millimeter-scale structures such as triangular and rectangular groove have been studied both theoretically and experimentally. However, secondary electron emission suppression capability of pillar array has only been studied theoretically in Ref. [16] without any experimental verification.

It is well-known that TSEY depends on several parameters, such as incident energy and angle[14] of primary electron, temperature,[19] and contaminations.[8] It is also widely known that typical yield–energy curve is of a single-hump shape.[20] What is more, if expressed in reduced form, the yield–energy curve for various materials can be described by a universal curve.[20] However, based on both our own experiences on TSEY measurement and data presented in published work,[19,21] it was found that the yield–energy curve may be of a double-hump shape. As shown in Fig. 1, both Mata et al.[19] and Wang et al.[22] observed this anomaly when they were characterizing roughened surfaces. However, as far as we know, this phenomenon still lacks interpretation. Although yield–energy curve with a double-hump shape has been reported for double-layered materials in Ref. [21], the interpretation there is unable to explain the observations from roughened surfaces as presented in Fig. 1.

Fig. 1. The TSEY–energy curve showing an abnormal double-hump shape (reproduced from Refs. [19] and [22]). Wang et al. fabricated roughened surface with silver plated aluminum plates using laser etch technique, while Mata et al. reported secondary electron emission properties of polished and unpolished aluminum samples.

In this work, taking advantage of three-dimensional (3D) printing technology (i.e., selective laser sintering technology), a silver millimeter-scale pillar array is fabricated with the expectation to answer the two questions mentioned above. Through Monte Carlo simulations and TSEY measurements, we verify that pillar array is efficient for electron emission suppression, and an energy-dependent electron beam size results in a double-hump shape yield–energy curve.

2. Experimental observations

A schematic view of the fabricated pillar array is shown in Fig. 2(a). The diameter of the cylindrical pillar was 1 mm and the distance between centers of two adjacent pillars was 1.5 mm. The size of the bottom plate was 20 × 10 × 0.8 mm3, which is suitable for the adopted TSEY test system. The details of the TSEY measurement system were described in Ref. [14]. In total, an array of 4 by 10 pillars was fabricated. The height of the pillar was 4 mm. Figure 2(b) shows the photo of the 3D printed silver pillar array. A flat sample as the counterpart using the same fabrication process was also printed. After being ultrasonically cleaned in acetone, alcohol, and purified water for 5 minutes successively, the sample was placed into an ultrahigh vacuum system for TSEY test using sample current method. It should be noted that, as indicated by the specifications of the electron gun, there are two adjustable parameters that determine the electron beam spot size, namely the grid voltage and the focus voltage. However, in this work, these two parameters remained constant for all of the primary electron energies. During TSEY measurement, we positioned the sample to three different locations, as shown in Fig. 2(a). Points 2 and 3 were obtained by moving the sample with a step of 0.5 mm. The details on the radiation position will be presented in Section 3.2. Since the periodicity of the pillar array is 1.5 mm, its TSEY is expected to be repeatable for a 1.5 mm distance. As a comparison, we also measured a flat sample obtained from the same fabrication process.

Fig. 2. (a) Schematic view of pillar array and (b) photo of the printed pillar array.

The measured TSEYs of both flat surface and pillar array surface are shown in Fig. 3. In this work, we only consider the normal incidence. As described earlier, the pillar array was measured at three successive locations with 0.5 mm interval and thus three TSEY curves are shown in Fig. 3 which are denoted as points 1, 2, and 3. First, it can be seen that for the entire primary electron range (40–1500 eV), the pillar array shows obvious TSEY suppression effect compared with the flat sample. Second, the TSEY of the measured pillar array changes with electron beam radiation position when the primary electron energy is greater than ∼500 eV, while TSEY is almost independent of radiation position when the primary electron energy is no more than ∼500 eV. Finally, the yield–energy curves show an anomalous double-hump shape. These observations will be interpreted in the following section.

Fig. 3. TSEY measurement result of mm-scale silver pillar array and its flat counterpart.
3. Explanations of the experimental observations
3.1. TSEY suppression effect of mm-scale pillar array

Considering the theoretical work presented in Ref. [16], experimental observations shown in Fig. 2 confirm that the TSEY suppression effect of pillar array is induced by the shadowing effect; i.e., when secondary electrons emit from the bottom substrate, a part of them will impact the sidewall of the pillars and thus reduce the effective TSEY (i.e., the observed TSEY). For further interpretation, we use a similar Monte Carlo simulation method presented in Ref. [12] to simulate the TSEY of pillar array. It is worth pointing out that in this work, both backscattered electrons and true secondary electron are considered and all of the emitted electrons follow cosine distribution for their emission polar angle and uniform distribution for their azimuthal angle. In Ref. [16], pillar array was taken as ideal periodical surface by using periodical boundary condition. Furthermore, they did not consider the size of the electron beam spot. Thus, their derivation/simulation is more suitable for micro/nano-scale pillar array with infinite array size, or is more suitable for electron beam with large enough spot size. However, for mm-scale pillar array considered here, it is not suitable to either adopt periodical boundary condition or assume that the beam spot size is relatively large enough compared with pillarʼs diameter. Thus, we made our simulation model as close to the real case as possible. Namely, we consider finite array size and controlled electron beam spot size.

First, to demonstrate the TSEY suppression effect, we set up our simulation as follows: the electron beam spot size is set as 15 mm and the pillar array has a size of 15 × 15. The diameter, height, and interval of the pillar are the same as those used in Fig. 2. The center of the electron beam is aligned with the center of the pillar array, as shown in the inset of Fig. 4. Before running the Monte Carlo simulation, we calibrate the TSEY of flat surface using measurement results shown in Fig. 3. Here, calibration means adjusting the parameters of the phenomenological electron–solid interaction model[1] to make the simulated yield coincide with measurement. Simulation results are shown in Fig. 4. For comparison, the TSEY of flat sample is also shown. It can be seen that the TSEY of the flat surface shown in Fig. 4 is very close to the corresponding measurements shown in Fig. 3. Besides, simulated TSEY of pillar array demonstrates an obvious suppression effect; i.e., suppressed by ∼43%. This observation also agrees well with the prediction in Ref. [16]. It should be noted that due to the finite scale, it is reasonable to infer that a fraction of the TSEY is contributed by secondary electrons escaping from the edge of the pillar array. Namely, if taking the whole pillar array as a brick, then secondary electrons may escape from the sidewalls of this brick. This could be more obvious if the packaging density, defined as normalized area occupied by the top of the pillar, is lower and the aspect ratio, defined as the ratio between height and diameter of the pillar, is higher, such as in the cases considered in Ref. [16]. To avoid distracting the focus of this work, it is expected to discuss this problem in greater depth in the near future. It should be noted that with the simulation setup mentioned above, the double-hump effect cannot be reproduced.

Fig. 4. Simulation results of flat surface and mm-scale pillar array.
3.2. Explanations on double-hump TSEY–energy curve

The second and third observations mentioned earlier can be explained by considering the dependence of electron beam spot size on the primary electron energy. Due to the working principle of electron gun, its spot size may change with primary electron energy. Generally, the exact relation between spot size and primary electron energy usually depends on the detailed design of electron gun and its working condition. Although it may be possible to ensure consistent spot size by adjusting the setup parameters of the electron gun, for the measurement system used in this work, the spot size changes with primary electron energy from sub-millimeter to a number of millimeters. It is obvious that the following two cases will have different TSEYs. Case 1: all the primary electrons impact with the top of the pillar. Case 2: all the primary electrons impact with the bottom substrate on which pillars stand. These two extreme cases are possible if the electron beam spot is small enough. For the first case, its TSEY will be close to the TSEY of flat surface. For the latter case, its TSEY will be much lower due to the shadowing effect. More generally, for a predefined electron beam spot size and radiation position, it is very possible that the primary electrons radiate both the pillar top and the bottom substrate. Then, the TSEY in this situation will be determined by the combined effect of cases 1 and 2. Therefore, to explain the measurement results shown in Fig. 3, it is mandatory to characterize the electron beam spot size.

There are many measurement methods for electron beam spot size, such as Refs. [23] and [24]. Considering the available setup, we adopt the following method to estimate the size of the electron beam spot, as shown schematically in Fig. 5. We form a rectangular trench along the y-axis with a high aspect ratio in a bulk metal part which is called as detector. The electron beam is aligned with the z-axis. The width and height of the trench are W and H, respectively. The diameter of the electron beam spot is D. When moving the detector along the x-axis from left to right, the electron beam will first radiate the outside of the trench, then gradually radiate into the trench, and finally radiate the outside of the trench again. It is expected that the observed TSEY will vary with the detector location. With the knowledge of the geometrical size of the trench, electron beam spot size can be extracted from the observed TSEY–location curve.

Fig. 5. Schematic view of the estimation method for electron beam spot size.

To demonstrate how to extract electron beam spot size, we conduct some Monte Carlo simulations using a similar method in Ref. [12]. A typical dependence of TSEY on the radiation location is shown in Fig. 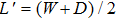6. The width of the trench is set as 2 mm while its depth is 4.5 mm, and the electron beam spot size is set as 1 mm. The movement step of the detector is set as 0.25 mm. It can be seen that a symmetrical TSEY–location curve is obtained. Three radiation positions, denoted as points A, B, and C, and the corresponding TSEY are marked in Fig. 6. Points A and C indicate the beginning of TSEY suppression while point B indicates the symmetrical point of the TSEY–location curve. It is straightforward that if one could obtain the distance L between points A and C, considering L = W+D, then the spot size is D = L−W. Or, to reduce the measurement effort, one can also try to find out points A and B. Then, the distance between these two points is . It should be noted that point B is the symmetry center of the TSEY–location curve. At this point, the TSEY may either reach a local maximum or minimum.

Fig. 6. Schematic of estimation method for electron beam spot size from TSEY.

To further demonstrate how the detector dimensions and electron beam spot size influence the observed TSEY, we conduct Monte Carlo simulations using parameters for copper presented in Ref. [1] and primary electron energy of 300 eV for the detector mentioned above and for spot size ranging from 0.05 mm to 8 mm. The movement step is set as 0.25 mm. The obtained results are shown in Fig. 7. From Fig. 7, one can accurately extract all the spot sizes except for the smallest spot of size 0.05 mm. However, if the movement step can be small enough, the 0.05 mm spot could also be characterized. It should be noted that since the adopted method highly depends on the movement step, the estimated spot size from this method may somehow present a notable error, especially for a large movement step.

Fig. 7. Simulated TSEY dependence on radiation position and electron beam spot size.

The experimental results of electron beam spot size are shown in Fig. 8. The detector is also fabricated by 3D printing using silver alloy. As in the simulation model described above, the depth of the trench is 4.5 mm and the width is 2.0 mm. To reduce the test effort, we select part of the primary electron energy ranging from 100 eV to 1500 eV to estimate the spot size for various primary electron energies. Totally speaking, the measurement process is the same as the usual TSEY test. For each measurement, we first make sure that the initial radiation position is the outside of the trench with the help of the embedded scanning electron microscope (SEM) function of the TSEY system. Then, we move the detector to make the electron beam gradually radiate into the trench. After some steps, we find that the TSEY begins to decrease, which indicates that part of the electron beam goes into the trench just like the case from point A to point B as shown in Fig. 6, and increases again after further movement, which indicates that part of the electron beam goes outside of the trench just like the case from point B to point C. It should be noted that only in the trench do we adopt a finer step to distinct the symmetrical point, which is denoted as the blue-dashed line on the right side in Fig. 8. It can be seen from Fig. 8 that when the primary electron is of higher energy, the symmetrical point is more recognizable. Thus, it is expected that the spot size is smaller for higher primary electron energy. For primary electron with an energy of 100 eV, the TSEY is almost independent of the radiation position, which indicates a large spot size for this case. Blue dashed lines are shown in Fig. 8 to help with the determination of spot size. The red-dashed lines represent the TSEY outside the trench. In Fig. 9, we show both the measured spot size represented by black square point, extracted from Fig. 8, and the estimated spot size represented by red circular point. These estimated spot sizes are obtained from linear interpolation based on the measured results. For low primary electron energy cases, we just take their spot size the same with 100 e; namely, the spot size is 7 mm for energies no more than 100 eV. In fact, the accurate spot size for energy below 100 eV is not so important since they do not affect the observed TSEY much as observed in our simulation. With the obtained spot size shown in Fig. 9, we conduct Monte Carlo simulation to reproduce the results shown in Fig. 3, and the simulation results are shown in Fig. 10. Compared with the measurement results, we find that our simulations agree well with the measurements. Thus, it is verified that the observations mentioned above are due to the energy-dependent spot size.

Fig. 8. The dependence of measured TSEY on radiation position for various primary electron energies.
Fig. 9. Measured and estimated spot size for various primary electron energies. The measured spot sizes are extracted from Fig. 8 while the estimated sizes are either from interpolation or from simplified assumption.
Fig. 10. The dependence of simulated TSEY on primary electron energy using spot size in Fig. 9. Namely, the spot size changes with primary electron energy. Other parameters are set as close to experiments as possible. The estimated radiation locations used here are described as follows.

To provide a more intuitional physical interpretation of the experimental results, in addition to the Monte Carlo simulation presented above, we also adopt a simple model, as shown in Fig. 11, to reproduce the double-hump phenomenon. With the help of Monte Carlo simulations and the measurements mentioned above, we obtain electron beam spot size and also the exact radiation position. The dot circles represent the electron beam spot, as shown in Fig. 11. For demonstration, we give two cases in Fig. 11; namely, 300 eV and 1000 eV. We also show the three different radiation locations labeled as points 1, 2, and 3, corresponding to Fig. 3. It can be inferred from Fig. 11 that for 1000 eV, point 2 will give a lower TSEY since most of the primary electrons are radiated into the intermediate trench between two adjacent pillars; while for 300 eV, not much difference will be expected since the overlapped area does not change a lot among the three points. These expectations agree well with the experimental results as shown in Fig. 3.

Fig. 11. The model that indicates the electron spot size effect.

We use the following procedure to evaluate the TSEY of the pillar array surface shown in Fig. 2. First, for the predefined electron beam radiation position and spot size, we calculate the overlapped area between the electron beam spot and pillars. In fact, this is realized by a classic Monte Carlo strategy: (1) a number of points are first uniformly distributed in the beam spot circle; (2) the overlapped area can be evaluated by counting up the number of points falling into the overlapped areas. Then, the TSEY is calculated using a weighted average as we used in Ref. [11], . Here, is the TSEY of pillar array, is the averaged TSEY of bottom part, and is the TSEY of flat surface. P is the porosity defined as the area ratio between the overlapped area and the whole electron beam area. It should be noted that TSEY for the bottom part in fact depends on the exact locations of the emission point. It is not surprising that the emission points close to a pillar will contribute less to the surfaceʼs TSEY due to the shadowing effect. To simplify the problem, we assume that the bottom part has a uniform TSEY which means that all the emission points have the same contribution to the TSEY of surface. As an approximation, we calculate this TSEY as follows. First, we calculate the porosity of pillar array which is 0.65; then, we take the simulated pillar TSEY shown in Fig. 4 (the lower curve) as a weighted average between the flat and bottom part, and thus we have . It should be noted that in order to simplify the problem, we have neglected the possible influence of non-uniform distribution of the electron beam intensity in this work.

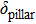
The calculation results are shown in Fig. 12. It can be seen that with the obtained energy-dependent electron beam spot size and initial radiation position, the experimental observations mentioned above are reproduced quite well. For the low energy part (such as 300 eV), the electron beam size is relatively large, thus the electron beam overlaps with several pillars. Therefore, in this energy regime, the surface has TSEY suppression effect and does not change much with the radiation position. For different radiation positions, the structures seen by the electron beam are almost the same. For higher energy regime, such as 1000 eV, the electron beam size is comparable to the pillar diameter. Thus, the TSEY is sensitive to the radiation position. When pillarʼs top contributes most of the TSEY, the observed TSEY is close to the flat case; otherwise, the observed TSEY is suppressed effectively compared with the flat surface. So, in the high energy range, TSEY is sensitive to the radiation position. In the double-hump effect, for a fixed radiation position, when the primary electron energy increases, due to the decreased spot size which will result larger weight of flat surface, TSEY may increase with the primary electron energy after it surpasses the first hump and result into a second hump. This explanation may also be used to interpret results shown in Fig. 1 while it is another mechanism for layer structures as presented in Ref. [20]. Furthermore, the results of this work demonstrate that roughened surface may have non-uniform TSEY and this could have some effect on real applications such as suppression of e-cloud effect.

Fig. 12. The TSEY calculation result with energy-dependent electron beam spot size. Points 1, 2, and 3 are defined as shown in Fig. 11. Points 1-0, 1, 2-0, 2, 3-0, and 3 are uniformly distributed in the same row with an interval of 0.25 mm.
4. Summary

In summary, we have analyzed the abnormal double-hump TSEY–energy curve both theoretically and experimentally. The 3D printed mm-scale pillar array, which shows both TSEY suppression effect and double-hump effect, is used for experimental verification. Monte Carlo simulations and simplified model are used to interpret observations. It is found that the double-hump effect is induced by the dependence of electron beam size on the primary electron energy; namely, the spot size decreases with the primary electron energy. Thus, one should care about the electron beam spot size when characterizing the TSEY of a material, especially for the case where the electron beam spot size is comparable to the characteristic structure of the surface.

Reference
[1] Furman M A Pivi M T F 2012 Phys. Rev. Spec. Top. Accel. Beams 5 124404
[2] Calatroni S Valdivieso E G Neupert H Nistor V Fontenla A T P Taborelli M Chiggiato P Malyshev O Valizadeh R 2017 Phys. Rev. Accel. Beams 20 113201
[3] Bronchalo E Á Coves Mata R Gimeno B Montero I Galán L Boria V E Mercadé L Sanchís K E 2016 IEEE Trans. Electron Devices 63 3270
[4] Li Y Ye M He Y N Cui W Z Wang D 2017 Phys. Plasmas 24 113505
[5] Jin C Ottaviano A Raitses Y 2017 J. Appl. Phys. 122 173301
[6] Pinto P C Calatroni S Neupert H Letant D D Edwards P Chiggiato P Taborelli M Vollenberg W Yin V C Colaux J L Lucas S 2013 Vacuum 98 29
[7] Suharianto A Michizono S Saito Y Yamano Y Kobayashi S 2007 Vacuum 81 799
[8] Zhang H B Hu X C Wang R Cao M Zhang N Cui W Z 2012 Rev. Sci. Instrum. 83 066105
[9] Ruzic D Moore R Manos D Cohen S 1982 J. Vac. Sci. Technol. 20 1313
[10] Cao M Zhang N Hu T C Wang F Cui W Z 2015 J. Phys. D: Appl. Phys. 48 055501
[11] Ye M He Y N Hu S G Hu T C Yang J Cui W Z 2013 J. Appl. Phys. 113 074904
[12] Ye M Wang D He Y N 2017 J. Appl. Phys. 121 124901
[13] He Y N Peng W B Cui W Z Ye M Zhao X L Wang D 2016 AIP Adv. 6 025122
[14] Ye M He Y N Hu S G Yang J Wang R 2013 J. Appl. Phys. 114 104905
[15] Wang D He Y N Ye M Peng W B Cui W Z 2017 J. Appl. Phys. 122 153302
[16] Swanson C Kaganovich I D 2016 J. Appl. Phys. 120 213302
[17] Valizadeh R Malyshev O B Wang S Sian T Cropper M D Sykes N 2017 Appl. Surf. Sci. 404 370
[18] Patino M Raitses Y Wirz R 2016 Appl. Phys. Lett. 109 201602
[19] Mata R Bañón D Socuellamos J M Gimeno B Boria V D 2017 Proceedings of 9th International Workshop on Multipactor, Corona and Passive Intermodulation (MULCOPIM’17) April 5–7, 2017 Noordwijk, The Netherlands Session 8B
[20] Walker C G H El-Gomati M M Assa’d A M D Zadražil M 2008 Scanning 30 365
[21] Yu S Jeong T Yi W Lee J Jin S Heo J Kimb J M 2001 Appl. Phys. Lett. 79 3281
[22] Wang D Ye M He Y N Li Y Cui W Z 2017 Proceedings of the 9th International Workshop on Multipactor, Corona and Passive Intermodulation (MULCOPIM’17) April 5–7, 2017 Noordwijk, The Netherlands Session 8B
[23] Bjärngard B E Chen G T Y Maddox B J 1975 IEEE T. Nucl. Sci. 22 1558
[24] Wei Y X Huang M G Liu S Q Liu J Y Hao B L Du C H Liu P K 2012 Vacuum 86 2109