† Corresponding author. E-mail:
First-principles calculations are performed to explore the possibility of generating the two-dimensional electron gas (2DEG) at the interface between LaGaO3/KTaO3 and NdGaO3/KTaO3 (001) heterostructures. Two different models—i.e., the superlattice model and the thin film model—are used to conduct a comprehensive investigation of the origin of charge carriers. For the symmetric superlattice model, the LaGaO3 (or NdGaO3) film is nonpolar. The 2DEG with carrier density on the order of 1014 cm−2 originates from the Ta dxy electrons contributed by both LaGaO3 (or NdGaO3) and KTaO3. For the thin film model, large polar distortions occur in the LaGaO3 and NdGaO3 layer, which entirely screens the built-in electric field and prevents electrons from transferring to the interface. Electrons of KTaO3 are accumulated at the interface, contributing to the formation of the 2DEG. All the heterostructures exhibit conducting properties regardless of the film thickness. Compared with the Ti dxy electrons in SrTiO3-based heterostructures, the Ta dxy electrons have small effective mass and they are expected to move with higher mobility along the interface. These findings reveal the promising applications of 2DEG in novel nanoelectronic devices.
Oxide heterostructures have emerged as a powerful platform for discovering novel interfacial properties, such as magnetism[1] and superconductivity.[2, 3] One major area of interest within the field is the two-dimensional electron gas (2DEG) discovered at the interface between two insulators: LaAlO3 (LAO) and SrTiO3 (STO).[4] The 2DEG with high sheet carrier density is particularly notable for its potential applications in nanoelectronic devices.[5] The mechanism of formation of the 2DEG remains a primary concern and several theories have been proposed. Electronic reconstruction due to the polar discontinuity,[6–8] oxygen vacancies in STO,[9–12] and the cation intermixing across the interface[13, 14] have been considered to be responsible for the interfacial conductivity. The origin of the 2DEG formed at the interface has been investigated both in theory[15–18] and experiment.[9, 19–24]
So far, most of the investigations of the 2DEG focus on the oxide heterostructures based on STO substrate, such as the following [25, 26] [27] [28] [29] [30–33]
 |

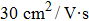

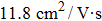
In this article, a comprehensive study of LGO/KTO and NGO/KTO heterostructures in two different models is carried out by using first-principles calculations to explore the possibility of generating the 2DEG at the interfaces. First, it is found that the 2DEG can be produced at LGO/KTO and NGO/KTO heterointerface in the symmetric superlattice model. The electrical properties are studied and the origin of the 2DEG is discussed. Then, in the thin film model we find that the metallic properties of LGO/KTO and NGO/KTO heterointerface are independent of the film thickness. The reason why there is no transition from insulating to metallic for LGO/KTO nor NGO/KTO in the thin film model is explained and the stability of the interface is explored.
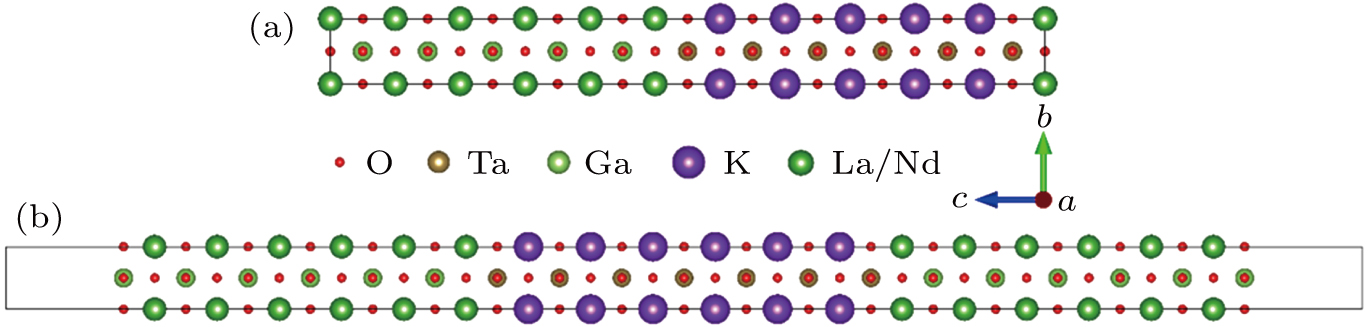
For both LGO/KTO and NGO/KTO heterostructures, two different models, i.e., the superlattice and the thin film model, are used to investigate the geometrical and electronic structures, as shown in Fig. 
KTO has a cubic phase with space group 
To investigate the intrinsic properties of the interface, the periodic superlattices are used due to no surface in this model. The band structure of (LGO)5.5/(KTO)5.5 and (NGO)5.5/(KTO)5.5 superlattice are obtained and shown in Fig. 

 |







 | Fig. 3. Conduction bands near Fermi energy for (a) (LGO)5.5/(KTO)5.5 and (b) (NGO)5.5/(KTO)5.5 superlattice, with vertical dashed line indicating Fermi energy located at 0 eV. |
To investigate the spatial distribution of the electronic states in more detail, the orbital-resolved partial density of states (DOS) for Ta atoms of each layer in LGO/KTO surperlattice is obtained and plotted in Fig. 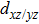


 | Fig. 4. Orbital-resolved partial DOS of (a) Ta dxy states and (b) Ta 
|
The relative displacement between anion and cation in each layer along the c axis of the LGO/KTO and NGO/KTO superlattices are calculated, and shown in Fig.
The advantage of the thin film model is that the calculated results compare well with the experimental observations by introducing the polar field in the thin film. Generally, a threshold thickness of the thin film is needed to form the metallic interface for the oxide heterostructures with STO substrate, such as LAO/STO, LGO/STO, and NGO/STO. In our calculations it is noted that the LGO/KTO (or NGO/KTO) systems are all metallic when the thickness of LGO (or NGO) varies from 1 u.c. to 10 u.c. Our calculations are in good agreement with previous results about LAO/KTO,[39] indicating that there exists no such threshold thickness in KTO-based heterostructure. It is worth mentioning that Wang et al. found that there is an overlap between the valence band maximum (VBM) and the CBM for the LAO/KTO system when the thickness of LAO is no less than 6 u.c.[39] However, such a behavior does not exist in our calculations, even when the thickness of LGO (or NGO) rises up to 10 u.c.
To understand the sources of this variation, the electronic structure of relaxed and unrelaxed (AGO)6/(KTO)6.5/(AGO)6 heterostructure are obtained. The layer-projected partial DOS for the fully relaxed and unrelaxed (LGO)6/(KTO)6.5/(LGO)6 system are compared as shown in figs. 

 | Fig. 6. Layer-projected partial DOS of (a) fully relaxed and (b) unrelaxed (LGO)6/(KTO)6.5/(LGO)6 heterostructure, along with the conducting electron charge density from −1 eV to the Fermi level. |
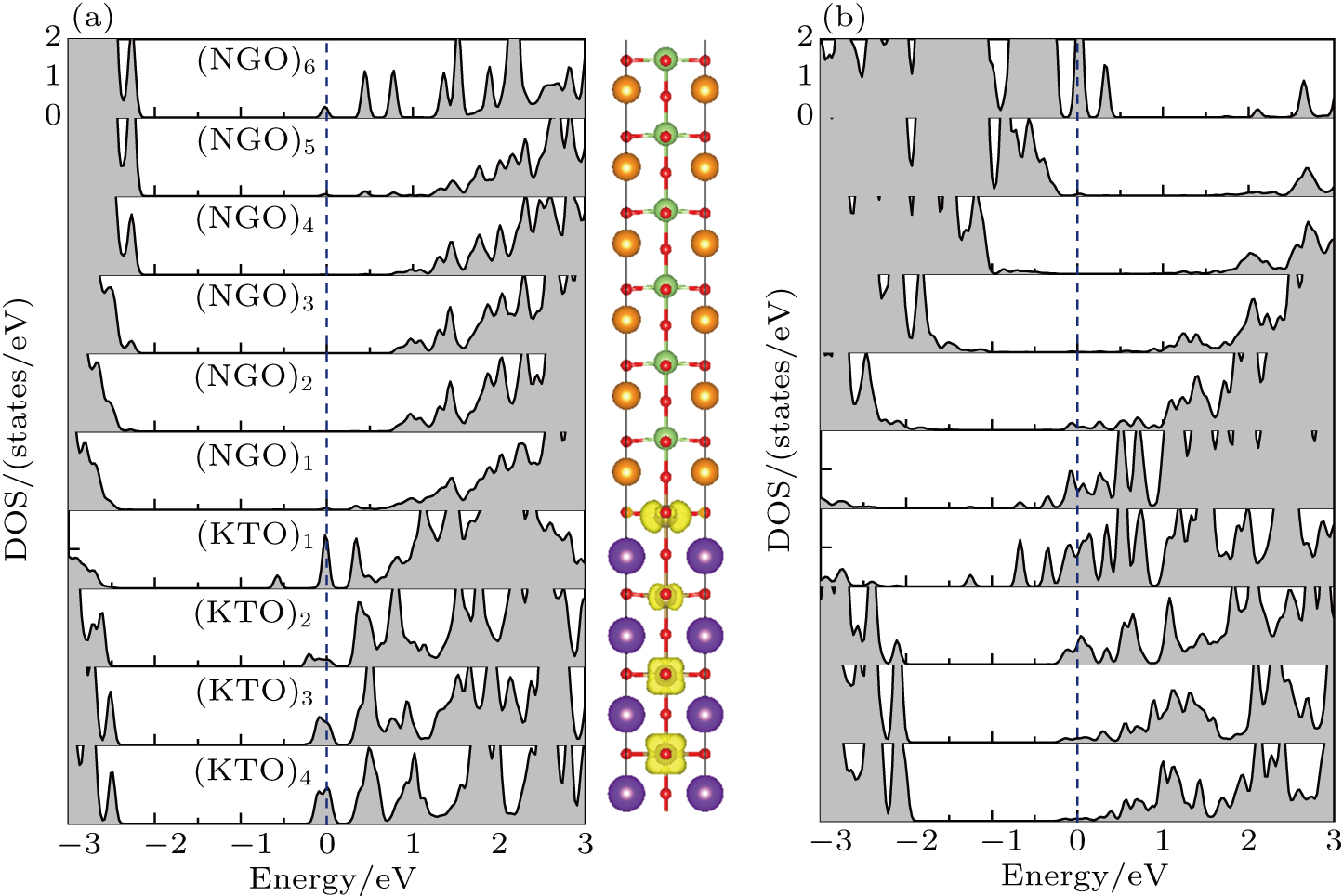 | Fig. 7. Layer-projected partial DOS of (a) fully relaxed and (b) (NGO)6/(KTO)6.5/(NGO)6 heterostructure, along with the conducting electron charge density from −1 eV to the Fermi level. |
This analysis indicates that the lattice distortions have a great influence on electrical properties. Figure
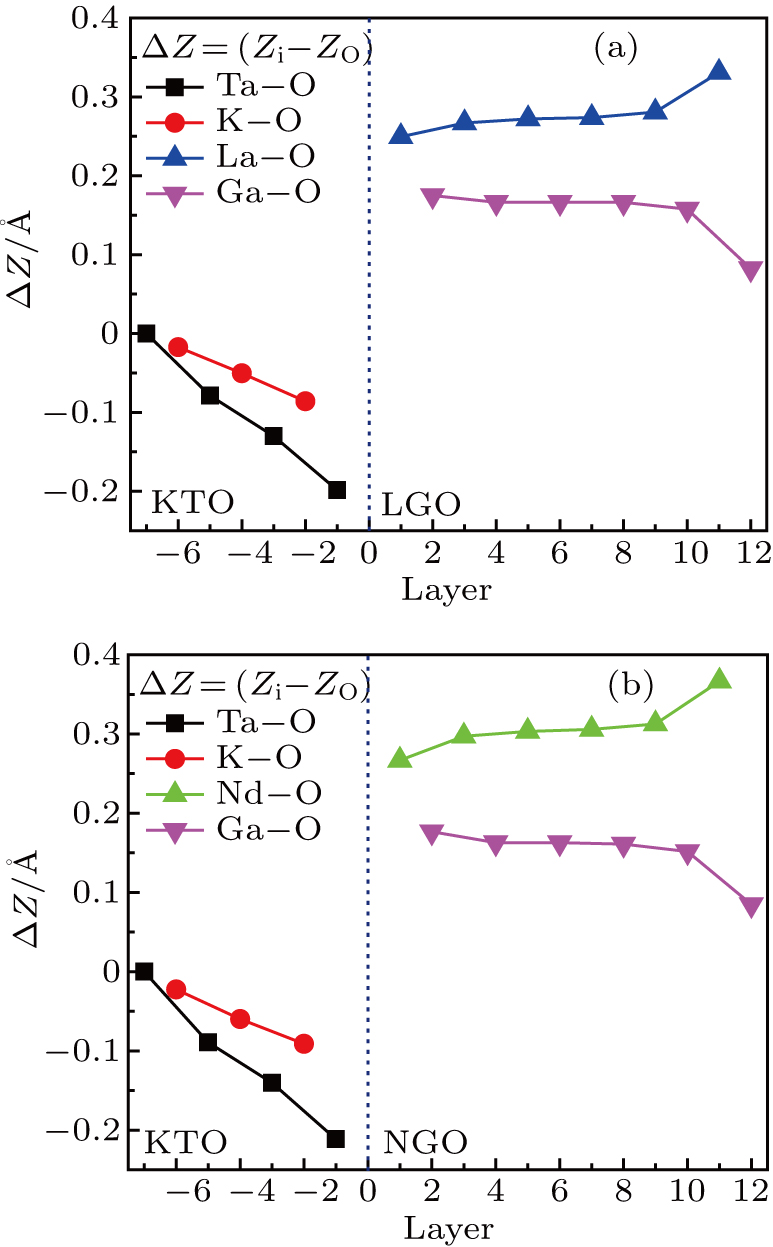 | Fig. 8. Relative displacements of the cations and the oxygen anions in each layer for panel (a) (LGO)6/(KTO)6.5/(LGO)6 and panel (b) (NGO)6/(KTO)6.5/(NGO)6 heterostructure along the c axis. |
To quantify the polarization strength, the polarization P within AGO film in AGO/KTO system is calculated from the following equation:[50, 51]
 |





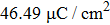

 | Fig. 9. Calculated polarization P in the AGO (A = La and Nd) films with respect to the AGO film thickness for the (AGO)m/KTO/(AGO)m (m = 1–10) heterostructures. |
Furthermore, the cleavage energy of LGO/KTO and NGO/KTO are calculated to evaluate the interfacial cohesion. The cleavage energy is given by[39]
 |


In this work, the possibility of generating the 2DEG in two different models of LGO/KTO and NGO/KTO heterostructure is explored by using first-principles density functional calculations. The 2DEG with a high carrier density of 1014 cm−2 is produced at LGO/KTO and NGO/KTO heterointerface in the symmetric superlattice model. In the thin film model, all the heterointerfaces are found to be metallic without an insulator-to-metal transition. The interfacial carrier density of the 2DEG is about an order of magnitude lower than that in the superlattice model because large polar distortions in the LGO and NGO layers greatly screen the built-in electric field and prevent electrons from transferring to the interface. The partially filled Ta dxy orbital is the origin of the 2DEG. The Ta dxy electrons with smaller effective mass in KTO-based heterostructure are expected to move with higher mobility along the interface. Our calculations are helpful in understanding the 2DEG and have important implications for developing new heterostructure hosting superior 2DEG.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |