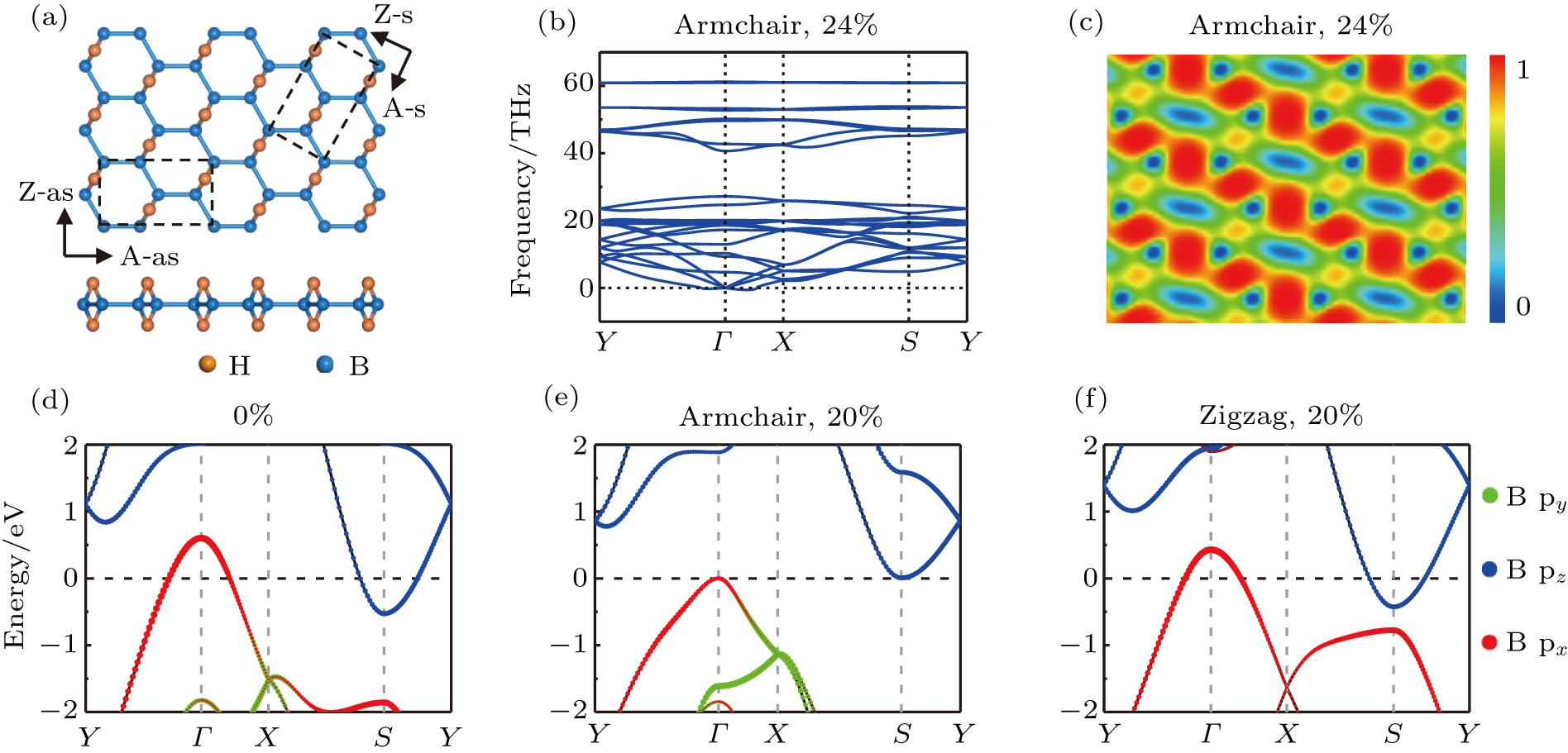
† Corresponding author. E-mail:
Freestanding honeycomb borophene is unstable due to the electron-deficiency of boron atoms. B2H2 monolayer, a typical borophene hydride, has been predicted to be structurally stable and attracts great attention. Here, we investigate the electronic structures of B2H2 nanoribbons. Based on first-principles calculations, we have found that all narrow armchair nanoribbons with and without mirror symmetry (ANR-s and ANR-as, respectively) are semiconducting. The energy gap has a relation with the width of the ribbon. When the ribbon is getting wider, the gap disappears. The zigzag ribbons without mirror symmetry (ZNR-as) have the same trend. But the zigzag ribbons with mirror symmetry (ZNR-s) are always metallic. We have also found that the metallic ANR-as and ZNR-s can be switched to semiconducting by applying a tensile strain along the nanoribbon. A gap of 1.10 eV is opened under 16% strain for the 11.0-Å ANR-as. Structural stability under such a large strain has also been confirmed. The flexible band tunability of B2H2 nanoribbon increases its possibility of potential applications in nanodevices.
Borophene and its derivatives are important branches in two-dimensional (2D) materials.[1–6] While due to the electron-deficiency of boron, borophene monolayer has been predicted to be structural polymorphism.[7–10] Actually, early synthesized borophene tends to form buckled triangular lattice or planar triangular lattice mixed with different arrangements of hexagonal holes.[11,12] Recently, a planar honeycomb borophene has been synthesized on the Al surface,[13] which was stabilized by compensation charge from the substrate. But the intrinsic properties of honeycomb borophene are deeply affected by the substrate. To get a substrate-free hexagonal borophene, hydrogenation is an alternative strategy to stabilize the honeycomb borophene.[14]
Monolayer B2H2, a borophene hydride, consists of honeycomb boron network and bridge hydrogens. It contains three-center-two-electron (3c2e) B–H bonds and is predicted to be a stable structure.[15,16] Recently, B2H2 nanosheets are fabricated by exfoliation and complete ion-exchange between protons and Mg cations.[17] Its infinite two-dimensional monolayer sheet has been predicted to exhibit intriguing mechanical properties. B2H2 monolayer has also been predicted to undergo a metal-semiconductor transition by applying tensile strain along the zigzag direction with mirror symmetry.[18,19] For integrating into nanoelectronic devices, it is inevitable to manipulate infinite 2D materials into various patterns with finite size, such as nanotubes, nanoribbons, nanodots, and so on. As a reduced-dimensionality form of 2D materials, nanoribbons are extensively investigated.[20–23] Although the B2H2 sheets have been investigated, the knowledge about B2H2 nanoribbons, which may be used in nanoelectronic devices, is very limited.
In this paper, using quantum mechanical calculations based on density functional theory (DFT), we investigate the electronic structures of B2H2 nanoribbons. We have found that the electronic structure of B2H2 nanoribbons is sensitive to the ribbon width except for the zigzag ribbon with mirror symmetry (ZNR-s). Narrow ribbons show semiconducting character in general. When the ribbons get wider, a semiconductor-metal transition induced by ribbon width occurs. The possibilities of manipulation to the metallic feature of wide ribbons are further investigated by tensile strain. The armchair nanoribbon without mirror symmetry (ANR-as) and ZNR-s exhibit significant strain effect on band structure. When the strain exceeds a critical level, a band gap is opened. For ANR-as with a width of 11.0 Å, a gap of 1.10 eV is opened under 16% strain. In contrast, for armchair nanoribbon with mirror symmetry (ANR-s) and zigzag ribbon without mirror symmetry (ZNR-as), strain cannot open gap yet. Finally, we also briefly discuss the reasons for the difference in strain effects in 2D infinite B2H2 sheet. Above all, the tunability of B2H2 nanoribbon electronic properties indicates that it is easier to find application space in nanoelectronic devices.
For B2H2 nanoribbons, structure optimizations were performed using the plane-wave technique implemented in the Vienna ab initio simulation package (VASP).[24] The projected augmented wave method was used to describe the ion-electron interactions, in which the exchange–correlation functional was Perdew–Burke–Ernzerhof (PBE).[25,26] Numerical convergence was achieved with thresholds of 10−6 eV in energy and 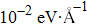
The atomic structure of B2H2 monolayer is made of in-plane hexagonal boron skeleton and out-of-plane bridged hydrogen pairs. The distance between the two boron atoms bridged by two hydrogen atoms is 1.81 Å, which is longer than the B–B bond length without hydrogen (1.71 Å). The B–H bond distance is 1.33 Å. The electronic property of this B2H2 monolayer exhibits metallic character.[15,16,18]
We first explore the band gap dependence on the width of B2H2 nanoribbon. For 2D honeycomb material, such as graphene, the commonly researched direction of nanoribbon is along high symmetry direction, that is, armchair and zigzag direction. As for B2H2, its high symmetry direction can be classified into two unequal directions, depending on the presence or absence of the mirror symmetry, as shown in Fig.
An ANR-as with a width of 5.1 Å presents a semiconducting feature with a gap of 0.33 eV. When the width increases, the band gap decreases. Figure
The ZNR-as with a width of 5.9 Å is also a semiconductor with a gap of 1.04 eV, as shown in Fig.
As shown above, all four types of B2H2 ribbons are metallic when they are wider than 8.1 Å. We then investigate the possibility to switch the wide ribbons to semiconductors by applying tensile strain which is plausible due to the flexibility of B2H2. The experimentally applied strain on the 2D sample which is synthesized on substrate is usually less than 7% because of the limited elastic property of substrate. While for suspended 2D materials, the limited strain can be broken through by mechanical nano-indentation using atomic force microscope (AFM).[29]
We start from the armchair nanoribbon without mirror symmetry. Taking the ANR-as with a width of 11.2 Å as the example, when the strain increases, the ribbon becomes narrow. When the tensile strain is 16%, the width of ANR-as is reduced to 11.0 Å, as shown in Fig.
We also investigate the strain effect of other ANR-as with different widths. As a 6.1-Å wide ANR-as, the strain-free ribbon is also metallic. When the strain increases to 8%, the VBM and CBM touch the Fermi level at Γ and X points, respectively. The ribbon begins to open a band gap if the strain continues to increase. When the strain is 18%, the gap reaches 1.39 eV. By studying the strain effect of different ribbon widths, we have found that a band gap can be opened under a certain tensile strain along the armchair direction.
The stability of nanoribbon under such a large tensile strain is then investigated by checking the existence of imaginary frequency, which is widely used in low-dimensional materials.[30,31] Figure
For a ZNR-s, a tensile strain along the zigzag direction can also open an energy gap. The band evolution of a wide ZNR-s has a similar trend to an ANR-as, as shown in Fig.
Applying a tensile strain along the armchair/zigzag direction cannot always open a band gap. For a wide ANR-s, the overlap of VBM and CBM, on the contrary, becomes larger under strain, as shown in Fig.
To further investigate why strain can open a gap in certain directions and cannot open gap in other directions, we study the strain effect on their 2D counterpart, B2H2 monolayer. Similar to the way to form B2H2 ribbons from cutting B2H2 monolayer, there are four crystalline directions in B2H2 monolayer (labeled in Fig.
Therefore, we have investigated the electronic properties of B2H2 monolayer under strain along the armchair direction and zigzag direction. As a reference, we also present our calculated electronic structure of a strain-free B2H2 in Fig.
The B2H2 monolayer under such a large strain is also structurally stable. In the case of applying strain along the armchair direction, when the strain is 24%, there is no imaginary frequency in the phonon dispersion, as shown in Fig.
In summary, the electronic structures of B2H2 nanoribbons have been systematically investigated. It is firstly demonstrated that the electronic structure of B2H2 nanoribbons is sensitive to the ribbon width except for ZNR-s. Narrow ribbons generally present semiconducting feature. When ribbons are wider, a semiconductor–metal transition occurs, which is induced by the width. Then the possibilities of manipulation to the metallic feature of wide ribbons are further investigated by applying tensile strain. Two types of nanoribbons, ANR-as and ZNR-s, exhibit significant strain effect on band dispersion. When the strain exceeds a critical level, a band gap is opened. For example, a gap of 1.10 eV is opened under 16% strain for the 11.0-Å ANR-as. In contrast, applying a strain cannot open a gap in ANR-s and ZNR-as. Finally, the reason for the difference in strain effects in various ribbon types has also been investigated. We have found that such difference is mainly contributed by its unique atomic structure in 2D infinite sheet. Above all, the tunability of B2H2 nanoribbon electronic properties indicates that it is easier to find application space in nanoelectronic devices.
A portion of the research was performed in CAS Key Laboratory of Vacuum Physics. Computational resources were provided by the National Supercomputing Center in Tianjin.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |