† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2017YFB0403003), the National Natural Science Foundation of China (Grant Nos. 61774081, 61322403, and 91850112), the State Key R&D Project of Jiangsu, China (Grant No. BE2018115), Shenzhen Fundamental Research Project, China (Grant Nos. 201773239 and 201888588), State Key Laboratory ofWide-Bandgap Semiconductor Power Electric Devices, China (Grant No. 2017KF001), and the Fundamental Research Funds for the Central Universities, China (Grant Nos. 021014380093 and 021014380085).
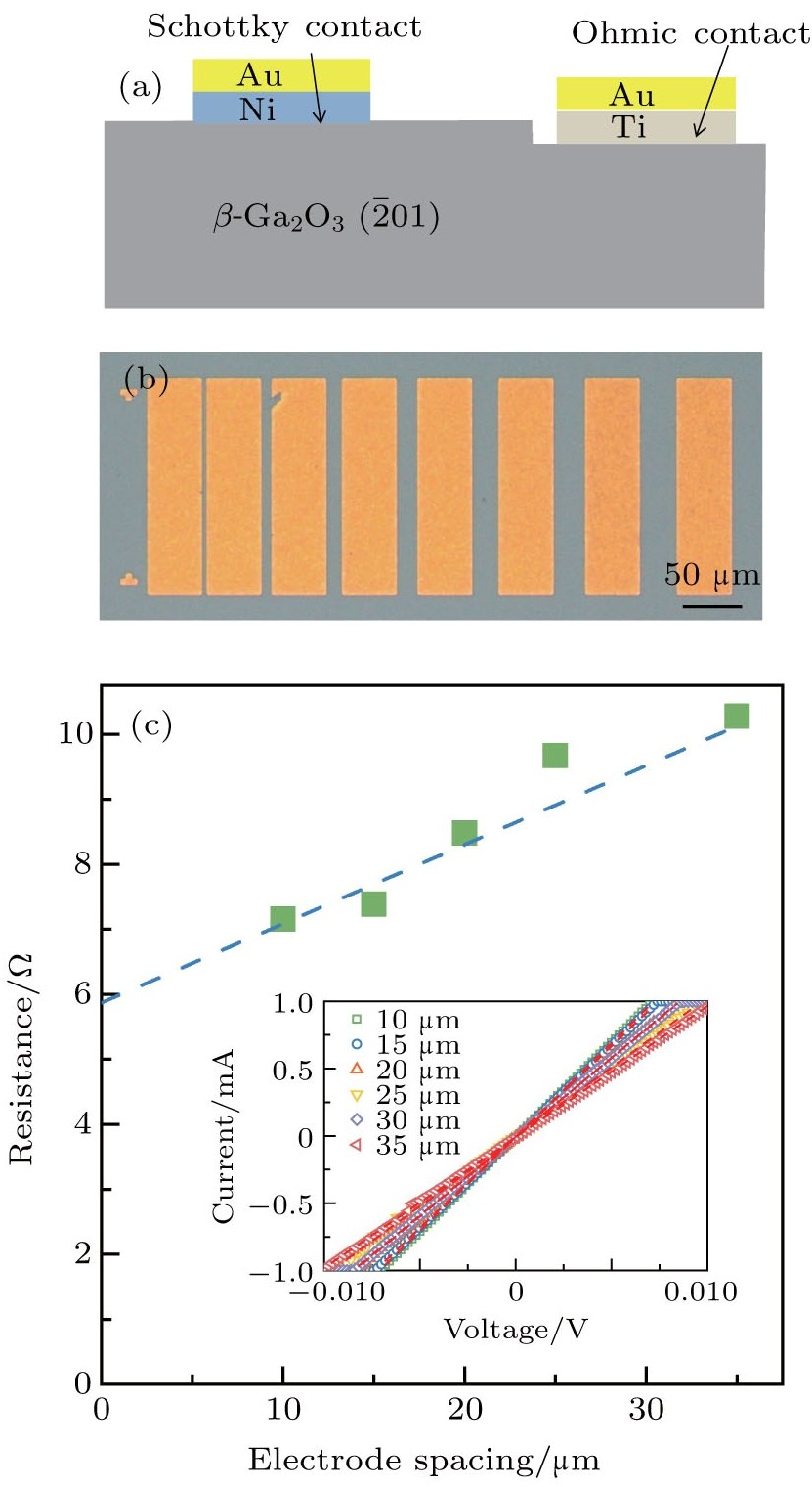
Ni/β-Ga2O3 lateral Schottky barrier diodes (SBDs) were fabricated on a Sn-doped quasi-degenerate n+-Ga2O3 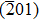
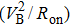
Ultra-wide bandgap (UWBG) semiconductors are promising for the delivery of power electronic devices and deep-ultraviolet solar-blind photodetectors with high energy conversion efficiency which have versatile applications in electric power, industrial control, consumer electronics, automotive electronics industries, flame detection, missile guidance, biochemical detection, and space communication.[1–7] Among these UWBG materials, β-Ga2O3 is attracting significant interest owing to its highly projected Baliga’s figure-of-merit (FOM) as a result of its wide-bandgap of 4.9 eV and large theoretical breakdown field of 8 MV/cm.[8–11] This is well in excess of the values of SiC and GaN, both of which are now established with commercial availability for high power devices. As β-Ga2O3 is one of the intrinsic solar-blind materials, state-of-the-art solar-blind photodetectors based on β-Ga2O3 Schottky diodes have been reported.[12–14] Compared to other UWBG materials including diamond and AlN, the availability of melt-growth methods to mass-produce single crystal β-Ga2O3 bulk substrates and the easy control of n-type doping provide important benefits towards low cost as well as the rapid development of epitaxial growth and device technologies. In recent years, rapid progress on the performance of field-effect transistors (FETs) and Schottky barrier diodes (SBDs) has been made.[15–22] With a low-doped drift layer grown by hydride vapor phase epitaxy (HVPE) and the integration of the field plates, vertical Schottky rectifiers with a breakdown voltage (VB) of over 1 kV have been demonstrated.[15] Very recently, with the employment of a trench structure, SBDs without optimized field management techniques showed a 1230 V breakdown voltage and a decent on-resistance (Ron,sp = 15 mΩ·cm2).[16] There are also recent advances in the edge termination method that suppress the electric field and enhance the reverse breakdown voltages.[17–22]
One of the merits of UWBG semiconductor-based SBDs is the improvement of their efficiency for applications in invertor circuits which need high current output. To date, most of the reported β-Ga2O3 SBDs are based on an unintentionally doped single crystal or thick epitaxial drift layer with a low carrier concentration. As a result, while the diode sustains extremely high critical electric fields, leading to large blocking voltages, high current output is limited. A trade-off between high breakdown voltage and high forward current output remains an unsolved issue. Further improvement in the efficiency and functionality of invertors relies on high current output and speed, which can be realized by low on-state resistances using highly-doped wide-bandgap semiconductors. However, SBDs directly fabricated on highly-doped quasi-degenerated Ga2O3 materials are still challenging. Recently, only Oishi et al. reported on the fabrication of vertical SBDs directly on β-Ga2O3 single crystals with a high electron concentration of 3.9×1018 cm−3.[23] Despite the fact that the diodes exhibit clear rectification characteristics with a current density of 96.8 A/cm2 at the forward voltage of 1.6 V, there is still much room for improvement in the device performance, and also the conduction mechanism of devices on quasi-degenerated β-Ga2O3 is not fully understood. In this work, we demonstrated improved performance of SBDs in lateral configurations on a weakly-degenerated β-Ga2O3 (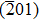
All bulk substrates used in this work were square-shaped pieces cut from commercial 2-inch diameter, 500 μm-thick Sn-doped n-type 9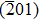
Transmission line measurement (TLM) methods were employed to characterize the specific contact resistivity of the Ohmic electrodes. The electrodes for TLM tests are Ti/Au metal stacks (100 nm/100 nm) which were fabricated and annealed under the same conditions as the Ohmic contacts described above. The rapid thermal annealing process has been optimized with the condition of 650 °C for 60 s to reduce the contact resistance. It was found that surface pre-treatment by ICP processing increased the surface roughness and generated large-density donor-like surface defects, which is helpful for enhancing the Ohmic features and decreasing the contact resistance.[24] After ICP treatment, TLM structures with channel lengths varying from 10 μm to 35 μm were fabricated, as shown in Fig.
Figure
 |
 |
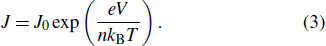 |
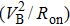
Linear plot of J–V characteristics of the β-Ga2O3-based Schottky diodes with a diameter of 100 μm measured at room temperature. The inset is the semi-logarithmic plot of forward J–V.
To evaluate the plausibility of various conduction mechanisms responsible for the observed leakage current, analytical modeling of electrical transport properties in reverse bias is necessary. For highly-doped weak-degenerated β-Ga2O3, the tunneling probability increases as electrons see a thinner barrier. It has been widely reported that the tunneling through thermionic field emission (TFE) becomes the favored transport phenomenon at reverse biases especially for high doping and intermediate temperatures.[25] Thermionic field emission takes place between field emission and thermionic emission.[25] When kBT ≈ E00, the tunneling electrons have energy between the Fermi level of the metal and the conduction band edge of the dielectric. In this work, the current density at reverse bias below −4 V could be fitted well by the TFE model, which is given by[26]
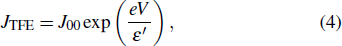 |
 |
 |
Furthermore, the evolution of reverse current at the high bias exhibits rather weak dependence on the applied voltages, which has also been observed in AlGaN-based Schottky diodes and is possibly contributed to by various field-enhanced tunneling mechanisms, such as the Pool–Frenkel (PF) emission, Fowler–Nordheim (FN) tunneling, or trap assisted tunneling (TAT) mechanisms.[25] When the reverse voltage is higher than −11 V, the length of the depletion layer is calculated to be larger than 80 nm and increases with the elevated bias. It was reported that the FN tunneling model becomes the dominant transport mechanism when the barrier is thin enough (< 100 Å).[27] Thus, the FN mechanism can be excluded and the PF emission model was also found to fail to describe the leakage current at high reverse bias.[28–30] As a matter of fact, the current transport can be understood well by the TAT mechanism as expressed by[31–32]
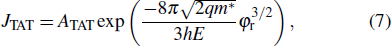 |
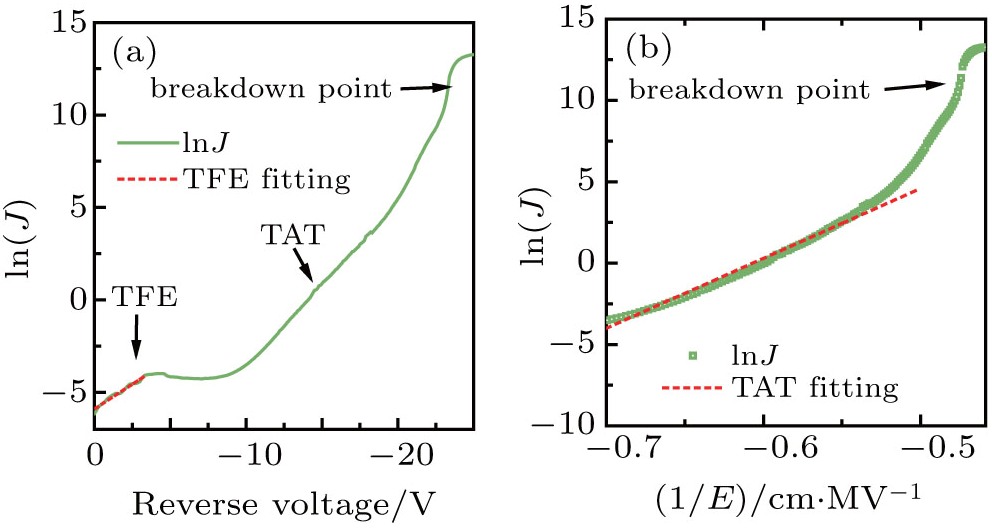 | Fig. 3. (a) Linear fitting of ln(J)–V at low field by TFE and (b) linear fitting of ln(J)–1/E at relatively high field by TAT. |
Figure
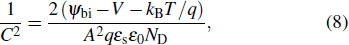 |
 |
 |
(a) The C–V characteristics and 1/C2–V plots of the Schottky barrier diodes at room temperature with 100 kHz sampling frequency. (b) Schematic energy band diagrams of the Schottky contact between Ni and β-Ga2O3.
Planar geometry Schottky diodes were fabricated based on highly-doped β-Ga2O3 (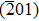
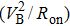
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |