† Corresponding author. E-mail:
Project supported by Guangdong Innovative and Entrepreneurial Research Team Program, China (Grant No. 2016ZT06D348), the National Natural Science Foundation of China (Grant No. 11874193), and the Shenzhen Fundamental Subject Research Program, China (Grant Nos. JCYJ20170817110751776 and JCYJ20170307105434022). The work at Brookhaven is supported by the US Department of Energy, Office of Basic Energy Sciences as part of the Computational Material Science Program (material synthesis).
We present a systematical study on single crystalline FeSb2 using electrical transport and magnetic torque measurements at low temperatures. Nonlinear magnetic field dependence of Hall resistivity demonstrates a multi-carrier transport instinct of the electronic transport. Current-controlled negative differential resistance (CC-NDR) observed in current–voltage characteristics below ∼ 7 K is closely associated with the intrinsic transition ∼ 5 K of FeSb2, which is, however, mediated by extrinsic current-induced Joule heating effect. The antimony crystallized in a preferred orientation within the FeSb2 lattice in the high-temperature synthesis process leaves its fingerprint in the de Haas-Van Alphen (dHvA) oscillations, and results in the regular angular dependence of the oscillating frequencies. Nevertheless, possible existence of intrinsic non-trivial states cannot be completely ruled out. Our findings call for further theoretical and experimental studies to explore novel physics on flux-free grown FeSb2 crystals.
FeSb2 exhibits a colossal Seebeck coefficient at low temperatures.[1,2] Electronic transport and magnetic measurements closely resemble rare-earth Kondo insulator, such as SmB6, YbB12, Ce3Bi4Pt3, and so on.[3–6] In a Kondo insulator, the hybridization of localized 4f states and d conduction bands drives the formation of a small insulating gap causing a metal-to-insulator transition (MIT) at low temperature, as in SmB6.[7] Besides the 4f electron system, iron-based Kondo insulator description is proposed for materials with localized 3d electron and noncubic lattice structure, such as FeSi and Fe2VAl.[8–10] FeSb2 features similar structure and physical properties with FeSi, and thus attracts considerable attention.[11–14]
Electrical transport measurements performed by several groups show a multi-carrier nature in FeSb2, accompanied by at least two main energy gaps of ∼ 30 meV and ∼ 5 meV.[15–17] From magnetic measurement, the thermally induced paramagnetic moment has been observed, as expected in Kondo insulator.[11,12] The colossal Seebeck coefficient of ∼ −45 mV/K near 10 K and high thermoelectric power factor (TPF) of ∼ 2300 μW/(K2 · cm), are the highest recorded in any material.[1,2] Nonetheless, these properties are highly sample- and impurity-dependent.[18,19] To date, the physical mechanism causing such high value of S is unresolved and could include electronic diffusion with strong correlations,[1,19,20] or phonon-drag effect.[2,21]
In this paper, we have investigated the electrical transport and magnetization properties on FeSb2 single crystals. Arrhenius plot and two-carrier model analyses are performed to obtain the band gaps and carrier information. Observation of current-controlled negative differential resistance (CC-NDR) may suggest some nonlinear dynamic characteristic at first glance. However, by careful experiments, an origin of thermal heating effect is identified. The de Haas-Van Alphen (dHvA) oscillations are observed in the magnetic torque measurements, which correspond to antimony crystallized in preferred orientation within the FeSb2 crystal during the crystal growth process.
FeSb2 single crystals were prepared by the method described in Refs. [11] and [12], then the as-grown crystals were oriented using a Laue camera and cut into small pieces with typical size of 0.8 mm × 0.4 mm × 0.1 mm. Electrical transport measurements were performed using standard four-probe method in an Oxford TeslatronPT cryostat with variable temperatures from 1.5 K to 300 K and a magnetic field up to 14 T. The current–voltage (I–V) characteristics were performed using the combination of Keithley 6221 current source and 2182A nanovoltmeter. The commercial Cernox thermometers were used to measure the temperature of the sample during the current–voltage measurements. Magnetic torque measurement was carried out using a homemade capacitance torque magnetometer similar as Ref. [35] [see Figs.
Figure
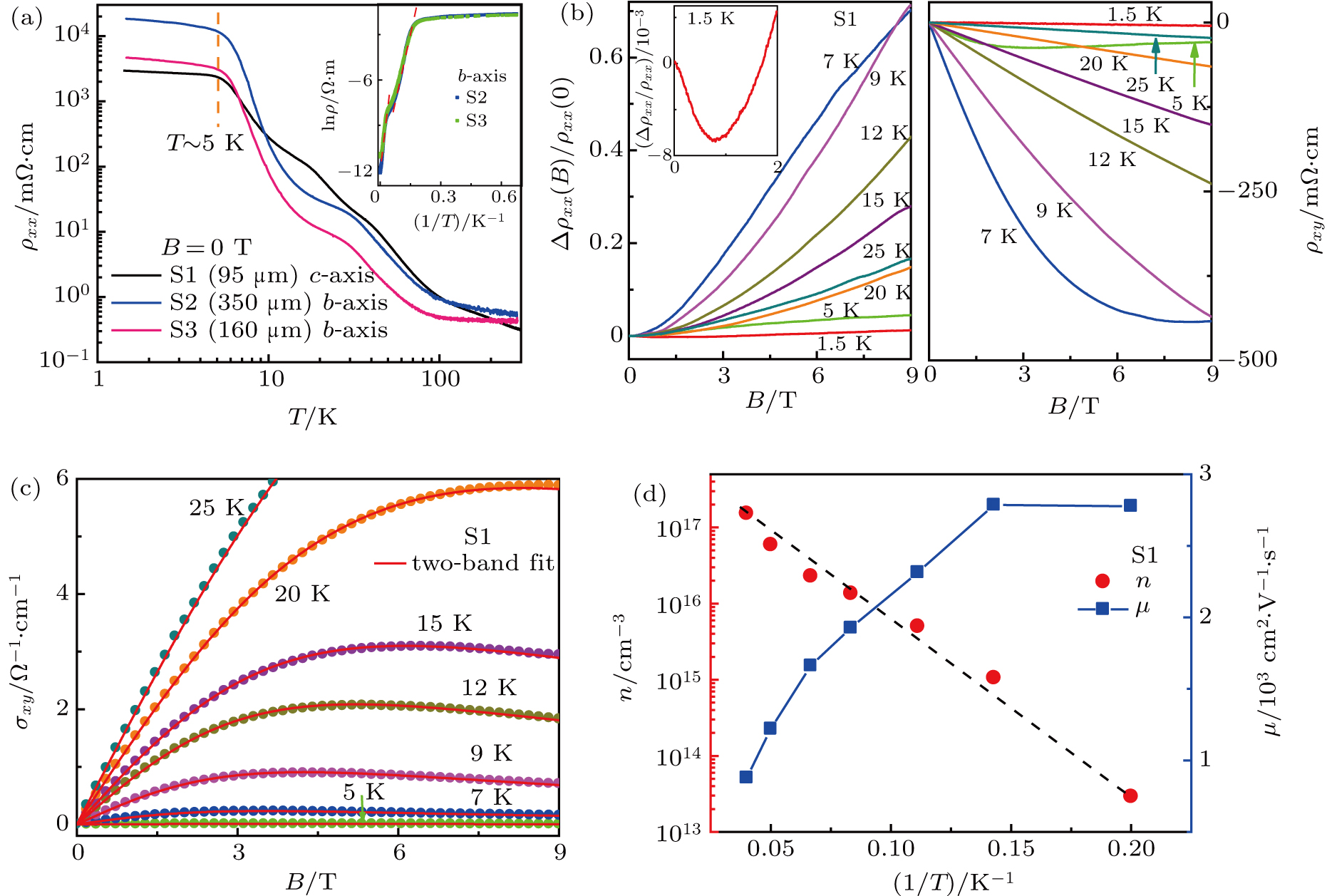
Magnetoresistivity (MR) ρxx and Hall resistivity ρxy measured at low temperatures for S1 are illustrated in Fig.
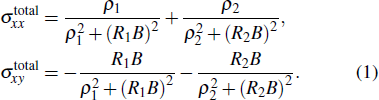 |
However, below 5 K, the two-carrier model is not applicable since the quantum coherence effect dominates the transport. Low-field negative MR appears in this temperature regime [see the inset of Fig.
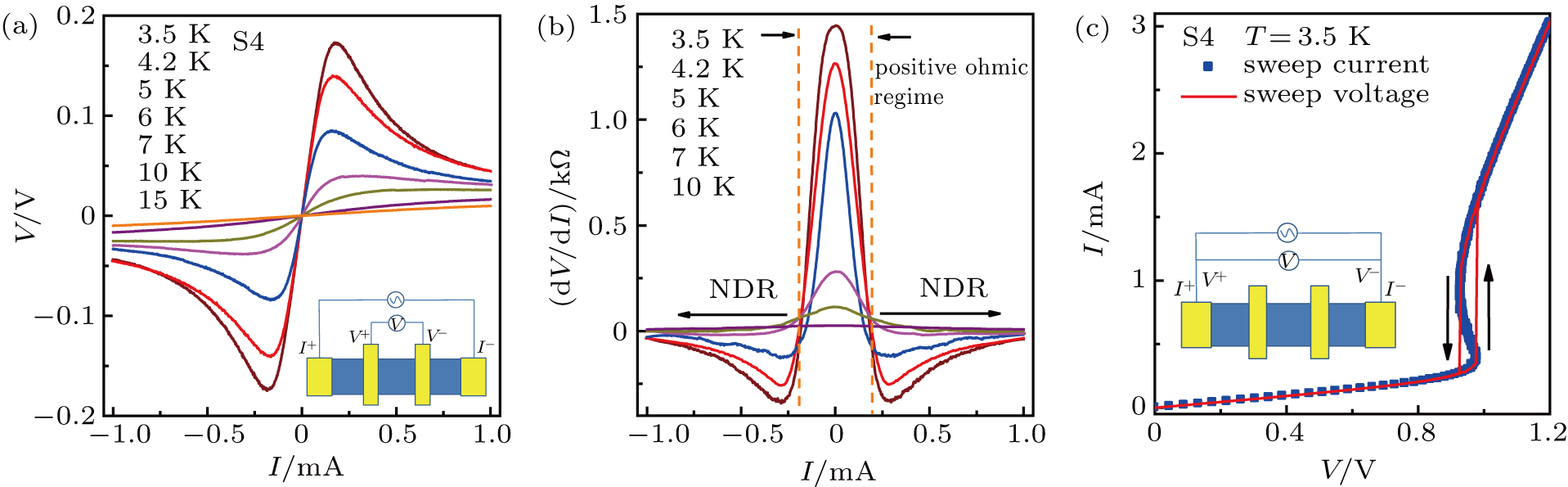
After obtaining the basic carrier information of the energy bands, we perform further current–voltage measurements to study the nonlinear characteristic of this material. Current-controlled negative differential resistance (CC-NDR) is clearly observed in our measurements. This exotic phenomenon has been reported experimentally in multiple material systems since the early 1960s, such as the oxides of V, Ti, Fe, and many other transition metals.[27–30] And theoretically, various mechanisms have also been proposed.[27–30] Most of these materials undergo a sharp metal-to-insulator transition (MIT) upon cooling and the observed CC-NDR in these systems naturally suggests the current-induced self-heating effect.[28,30,31] When a large current is applied, the sample is locally warmed up until the critical MIT temperature, above which the resistivity drops abruptly. This has an unstable positive feedback effect on the current and results in the formation of new conductive channels in bulk material.
Figure
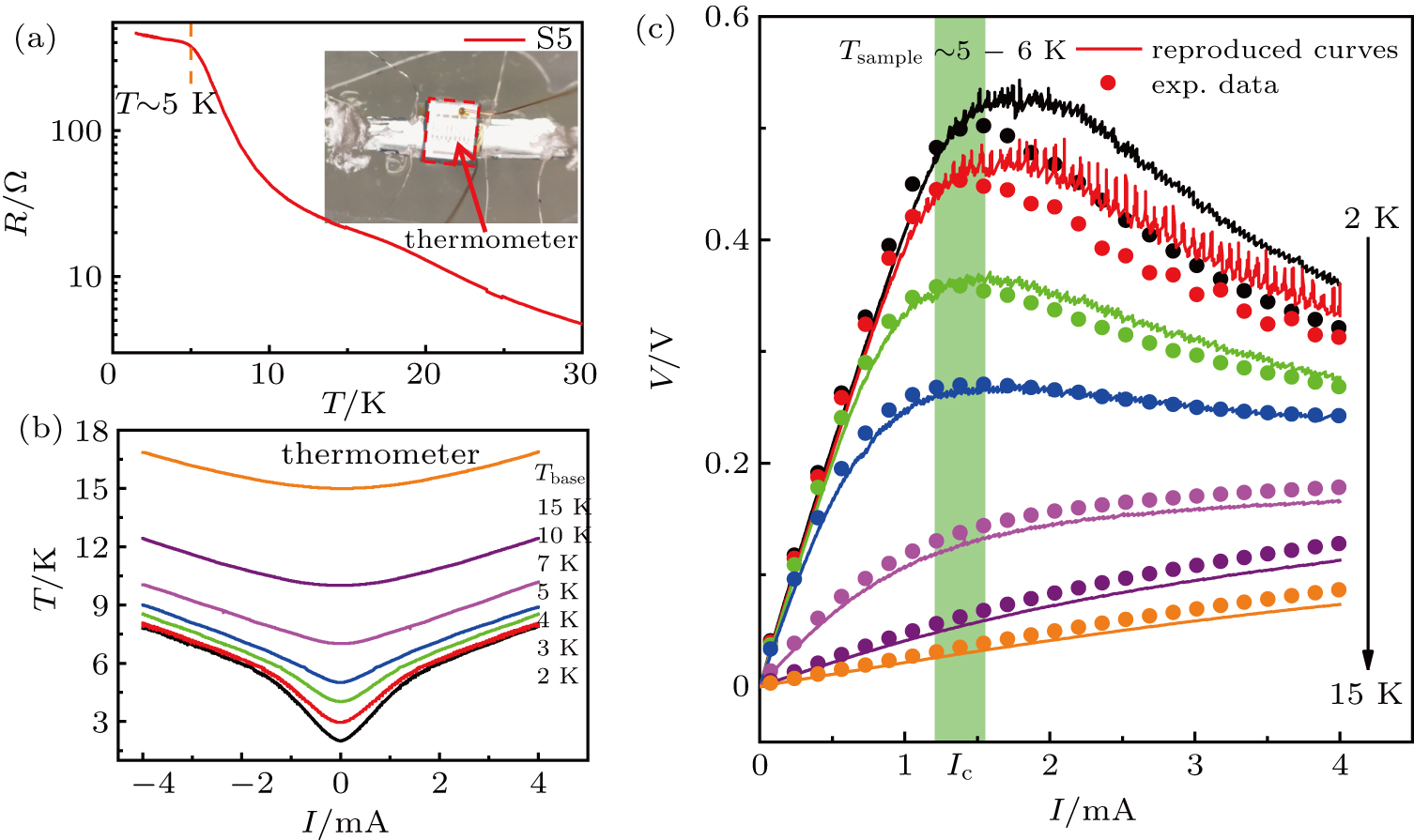
To clarify the underlying physical mechanism of this CC-NDR effect, contributions from Joule-heating effect were studied in detail. A Cernox thermometer was mounted directly on top of the sample using GE-varnish to ensure thermal anchoring and electrical insulation, as the cryostat base temperature cannot represent the real sample temperature when applying large current.[31] Each I–V curve was swept slow enough to maximize the thermalization between the sample and the thermometer. By this means, the readings of the thermometer closely represent the sample temperature. In the following, we adopt the thermometer temperature as sample temperature. Figure
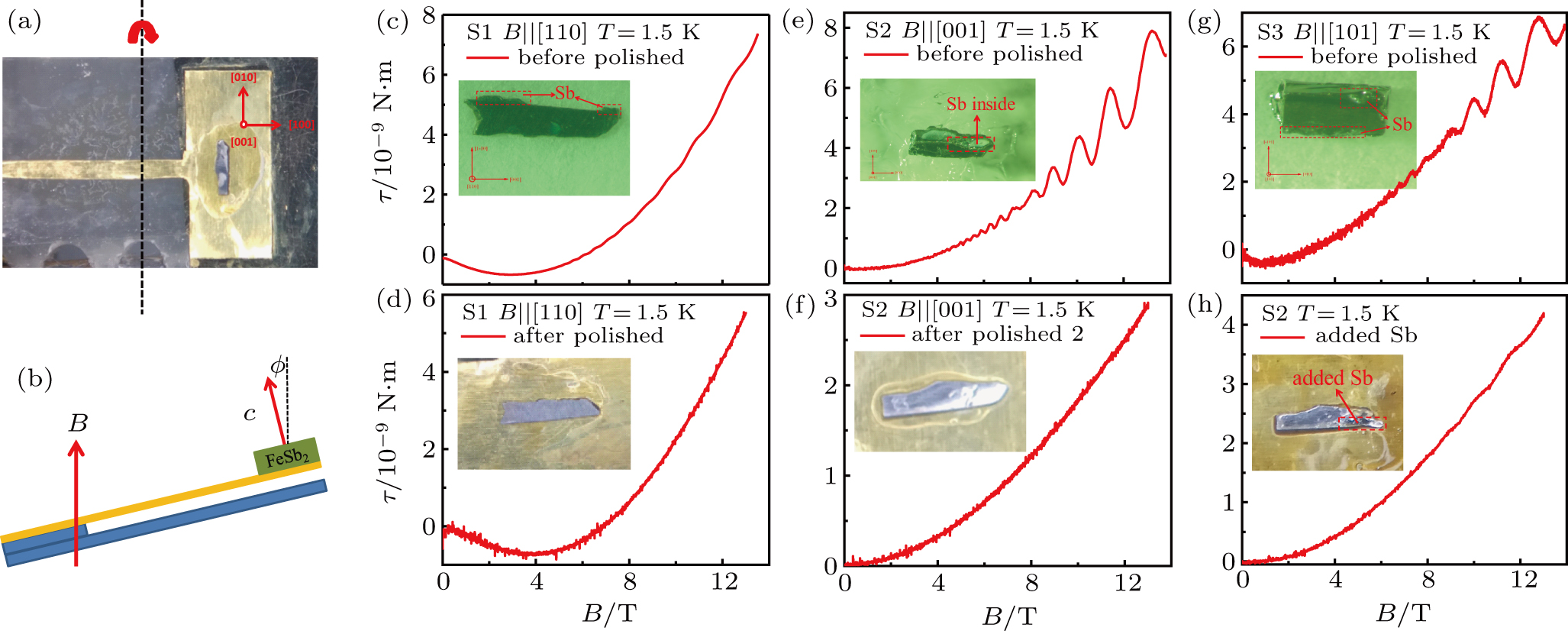
As discussed in previous section, saturation of resistivity at low temperature suggests the existence of a conductive state whose origin is unclear yet. These non-trivial transport properties remind us of the well-studied SmB6, in which a topological surface state is possibly realized.[31,34,35] Experimentally, dHvA oscillations have been probed in SmB6 by high precision magnetic torque measurements by Li et al.[35] and Tan et al.[36] The consensus on physical interpretation is, however, not accomplished. Li et al.[35] argued that a two-dimensional metallic surface state with light cyclotron mass (∼ 0.1 me) is responsible for the observed dHvA. In contrast, Tan et al.[36] found that the Fermi surface is three-dimensional and originates from the insulating bulk. Similar quantum oscillations arising from bulk insulating states were also observed both in magneto resistivity and magnetic torque measurements in another Kondo insulator YB12.[37]
In Fig.
We performed quantitative analysis on the observed quantum oscillations using temperature and angular-dependent torque measurements. In Fig.
 |
 | Fig. 5. (a) Amplitudes of the dHvA oscillations at different temperatures after subtracting a polynomial background. (b) Theoretical analysis according to Lifshitz–Kosevich formulation of the dHvA amplitudes for α pocket with field applied along two different directions, which gives a cyclotron mass ∼ 0.1me. (c) Angular dependences [schematic diagram seen in Fig. |
In Fig.
In conclusion, we have systematically investigated the electrical transport and magnetization properties on FeSb2 single crystals. Band gaps and carrier information were obtained using the Arrhenius plot and two-carrier model analysis. Current-induced negative differential resistance (CC-NDR) observed at low temperatures is associated with the non-trivial transition ∼ 5 K, which is triggered by current-induced Joule heating effect. The switching effect could play an important role in technological applications and provide a platform for the phase-space analysis in chaotic system. We found clear dHvA oscillations in torque experiments for our FeSb2 but may arise from antimony contaminations. More detailed theoretical and experimental studies are desired to investigate possible non-trivial states in this interesting system. We also anticipate this work of providing a new platform for physical studies and potential applications of Kondo insulator.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |