† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11434012, 11874061, and 41561144006).
Underwater acoustic applications depend critically on the prediction of sound propagation, which can be significantly affected by a rough surface, especially in shallow water. This paper aims to investigate how randomly fluctuating surface influences transmission loss (TL) in shallow water. The one-dimension wind-wave spectrum, Monterey–Miami parabolic equation (MMPE) model, Monte Carlo method, and parallel computing technology are combined to investigate the effects of different sea states on sound propagation. It is shown that TL distribution properties are related to the wind speed, frequency, range, and sound speed profile. In a homogenous waveguide, with wind speed increasing, the TLs are greater and more dispersive. For a negative thermocline waveguide, when the source is above the thermocline and the receiver is below that, the effects of the rough surface are the same and more significant. When the source and receiver are both below the thermocline, the TL distributions are nearly the same for different wind speeds. The mechanism of the different TL distribution properties in the thermocline environment is explained by using ray theory. In conclusion, the statistical characteristics of TL are affected by the relative roughness of the surface, the interaction strength of the sound field with the surface, and the changes of propagating angle due to refraction.
Underwater acoustic applications depend critically on the prediction of sound propagation, which can be significantly affected by the wind-caused fluctuating surface, especially in shallow water. Thus, fluctuating surface has important influence on underwater applications, such as underwater acoustic communication,[1,2] inversion of bottom absorption coefficients,[3] and matching-field localization.[4] This implies that it is essential to consider the effect of surface roughness on the performance evaluation of the underwater communication and estimate the influence of the wind-caused sea wave on the experiments before further processing and analyzing the received signals. Therefore, it is quite important to investigate how the randomly fluctuating surface affects sound propagation in shallow water.
Sound propagation is determined by boundary conditions to some extent. Generally, sea surface is modeled as a smooth interface, where the sound is specularly reflected. However, in the case of strong wind, the roughness and variation of the surface should be considered. Diffuse reflection from the rough surface makes sound ray stochastically scattered to disparate directions besides the specular reflection direction, leading to the attenuation and fluctuation of acoustic pressure at the receiver. Other effects include arrival time fluctuation,[5,6] signal coherence varyiation,[7–9] focusing and defocusing,[10] angle spreading,[11] frequency shifting, and bandwidth broadening.[12] In shallow water, since repeated surface–bottom interactions occur, these effects will be more significant.
Over the recent decades, there have been many papers discussing the effects of wind-generated fluctuating surfaces. Early research had reported the backscattering of sound signals for monostatic sonar systems.[13,14] While recent studies focused on forward scattering with the development of bistatic sonar systems. Kuperman found that the attenuation caused by surface scattering was affected by wind speed, sound speed profile, bottom properties, and wind directions.[15] Weston systematically examined the wind–wave–acoustics relation and concluded the fitting formula among scattering attenuation, wind speed, and frequency.[16] Wang reported that the significant difference of transmission loss (TL) in two underwater experiments resulted from the wind-caused rough surface.[3] Using experiments and large numbers of simulations in estuarine shallow water, Zou indicated a strong relation between surface roughness and pressure amplitude of broadband signals at the once-surface-reflected path.[17] Since wind-caused surface fluctuation is a random process, it is effective and reasonable to use statistical methods to study its effects, which will bring the challenge of large computing requirement in the simulation. Therefore, few researchers use these methods. While we have employed parallel computing to obtain the simulation results to be analyzed with these methods.
This paper uses a one-dimensional wind-wave spectrum for fluctuating surface generation and Monterey–Miami parabolic equation (MMPE) model to simulate the sound propagation under the rough surface. A parallel algorithm is proposed to speed up the simulation process and the Monte Carlo method is used to model the stochastic sound field. The purpose of this paper is to discuss the statistic characters of TL distribution caused by rough surface scattering under different wind-wave conditions in shallow water, and to introduce a rapid approach to evaluate the variation of TL for the fluctuating surface. This study is based on numerical simulations of an isothermal environment and a thermocline environment. As an innovation, we propose a rapid method to calculate the statistical properties of TL under randomly fluctuating surface.
The remainder of the article is organized as follows. Section
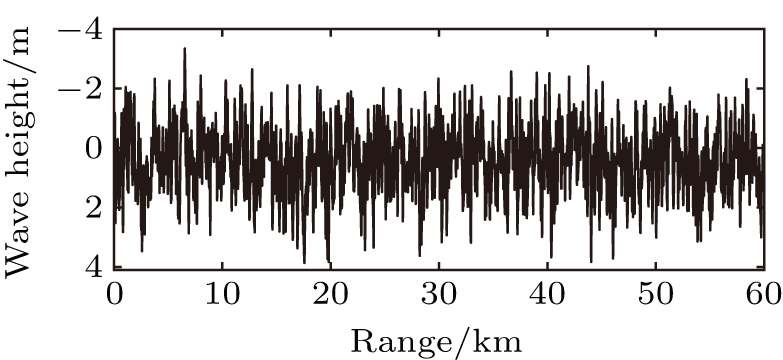
In this paper, a one-dimensional wind-wave spectrum is used to generate stochastically fluctuating surfaces.[18] In two-dimensional coordinates (r,z), the surface interface is defined as follow:
 |
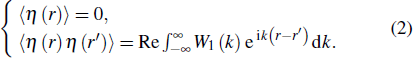 |
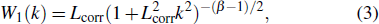 |
 |
 |
In order to compute stochastic realizations of roughness, superimpose a component Aeiθ upon the wave spectrum W1(k), consisting of a random wavenumber amplitude 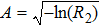
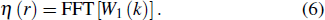 |
The MMPE acoustic propagation model was proposed by Kevin B. Smith[20] based on UMPE model[18] using the split-step Fourier (SSF) algorithm[21] to solve the parabolic equation (PE). The MMPE model is only capable of computing fields scattered from a flat surface. So, a field transformation approach that allows for the calculation of rough surface scattering is used in this paper, which was introduced by Tappert and Nghiem-Phu.[22]
In the MMPE Model, the waveguide is considered as a constant-density medium in cylindrical coordinates (r,z,φ) and a point source of unit strength is set at coordinates (r = 0, z = zs, φ = 0). The Helmholtz equation is
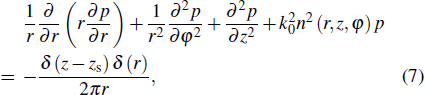 |
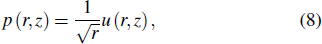 |
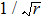
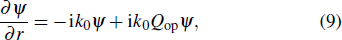 |
 |
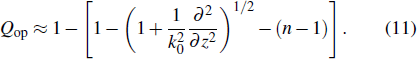 |
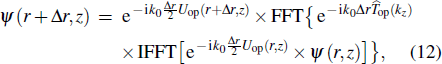 |
 |
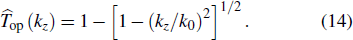 |
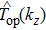
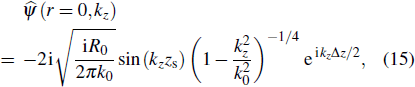 |
To satisfy the boundary condition of smooth pressure release surface, ψ(z = 0) = 0, assume an identical image ocean overlays the real ocean for the negative values of depth. The PE field function is exactly equal but of opposite sign in the image ocean, i.e.,
 |
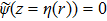
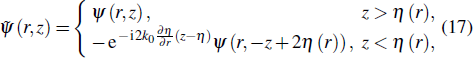 |
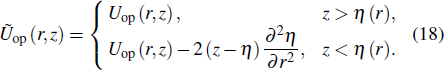 |
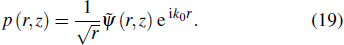 |
The Monte Carlo method, also called the statistical simulation method, is to use statistic experiment of random variables to simulate the solution of mathematic, physical, and engineering problems.
For the randomness of the sea surface, from which the sound wave is scattered, the TL at the receiver is randomly fluctuating as well. The Monte Carlo method is used to obtain the distribution of TL. According to Subsection
Generally, the TL of a single frequency signal is vibrating with the range because of the interference between normal modes. To get smoother TL curve, we average the sound energy of N discrete frequencies within 1/3 octave band width around the center frequency,
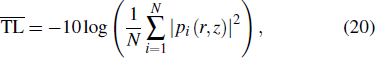 |
To reduce the processing time, a rapid algorithm is proposed based on parallel computing, in which multiple processes are executed simultaneously to complete a large number of calculations quickly. The parallel algorithm is based on a message passing interface (MPI), a message passing library specification. The library routines are called from Fortran programs to accomplish communication between processes.[24]
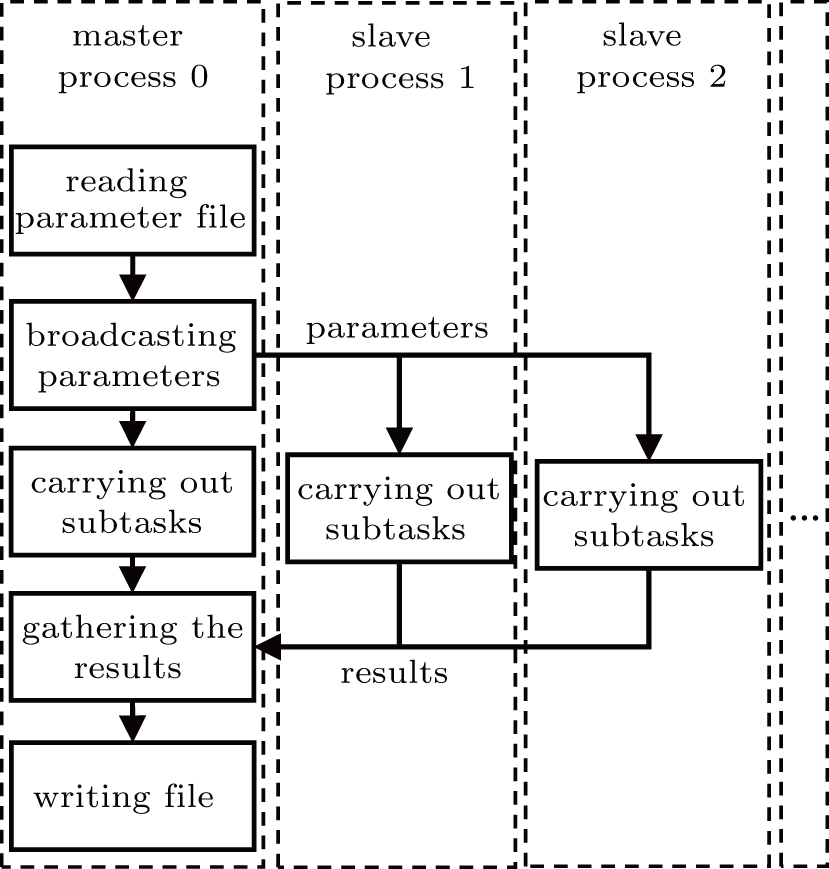
In this algorithm, a subtask is defined as sound field prediction of a single frequency under a rough surface. Executed on m cores of a multi-core computer, it is most time saving to allocate all subtasks equally to the m processes. The field calculating procedure of each subtask is independent of the others. Thus, the problem could be easily parallelized and communication between processes only occurs at the start and the end of the program to deliver the parameters and gather the results.
The parallel MMPE algorithm is designed in the master–slave mode, as shown in Fig.
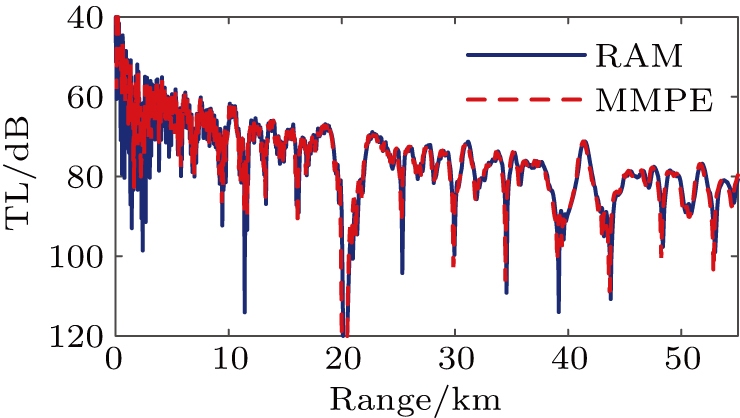
The validity of the parallel MMPE program is illustrated through a comparison with the RAM model. In the waveguide of Fig.
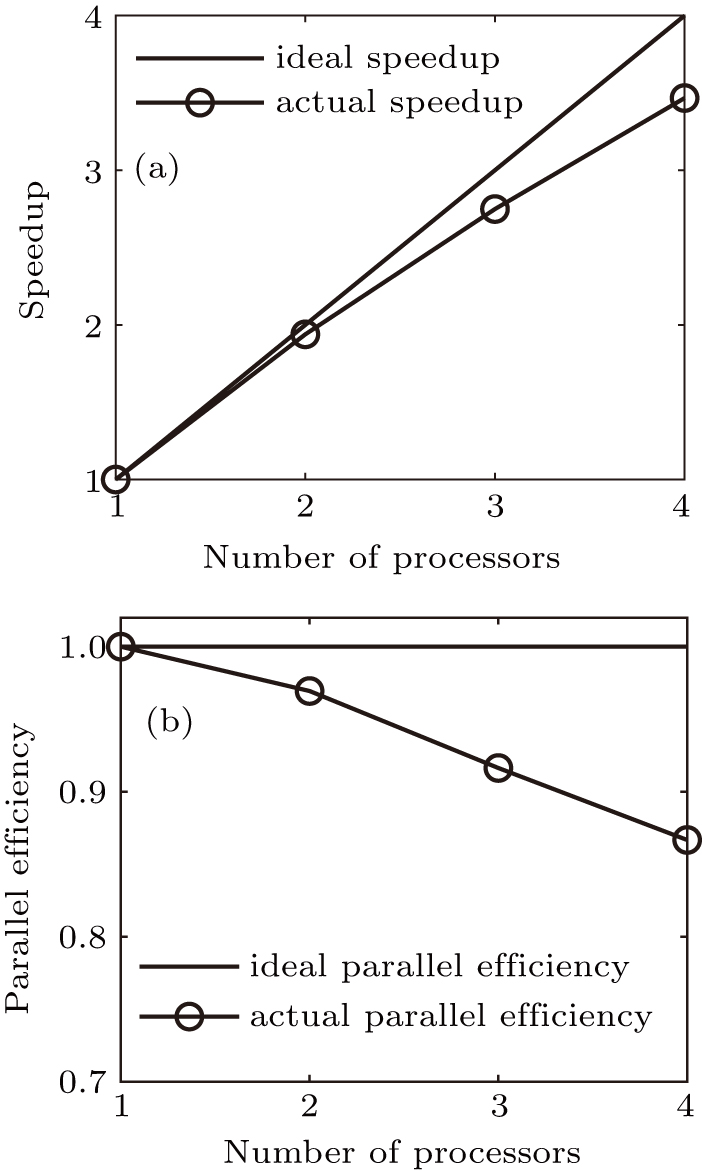
The performance of the parallel program is measured by both the speedup ratio Sm and the parallel efficiency Em, which are defined as follows:
 |
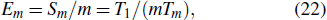 |
A typical range-independent homogenous waveguide in the South China Sea is used,[3] as displayed in Fig.
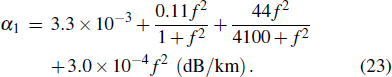 |
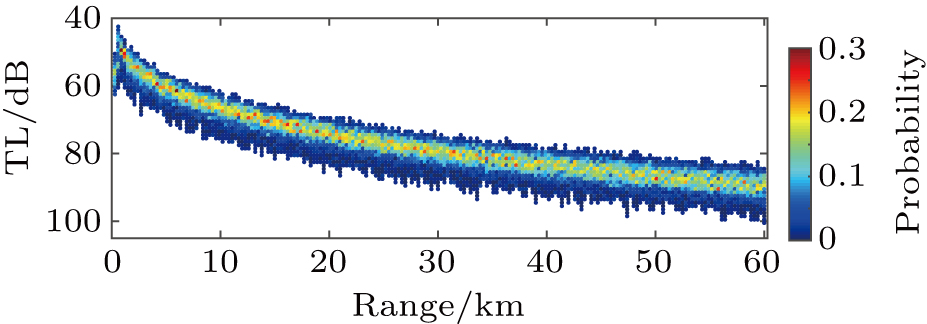
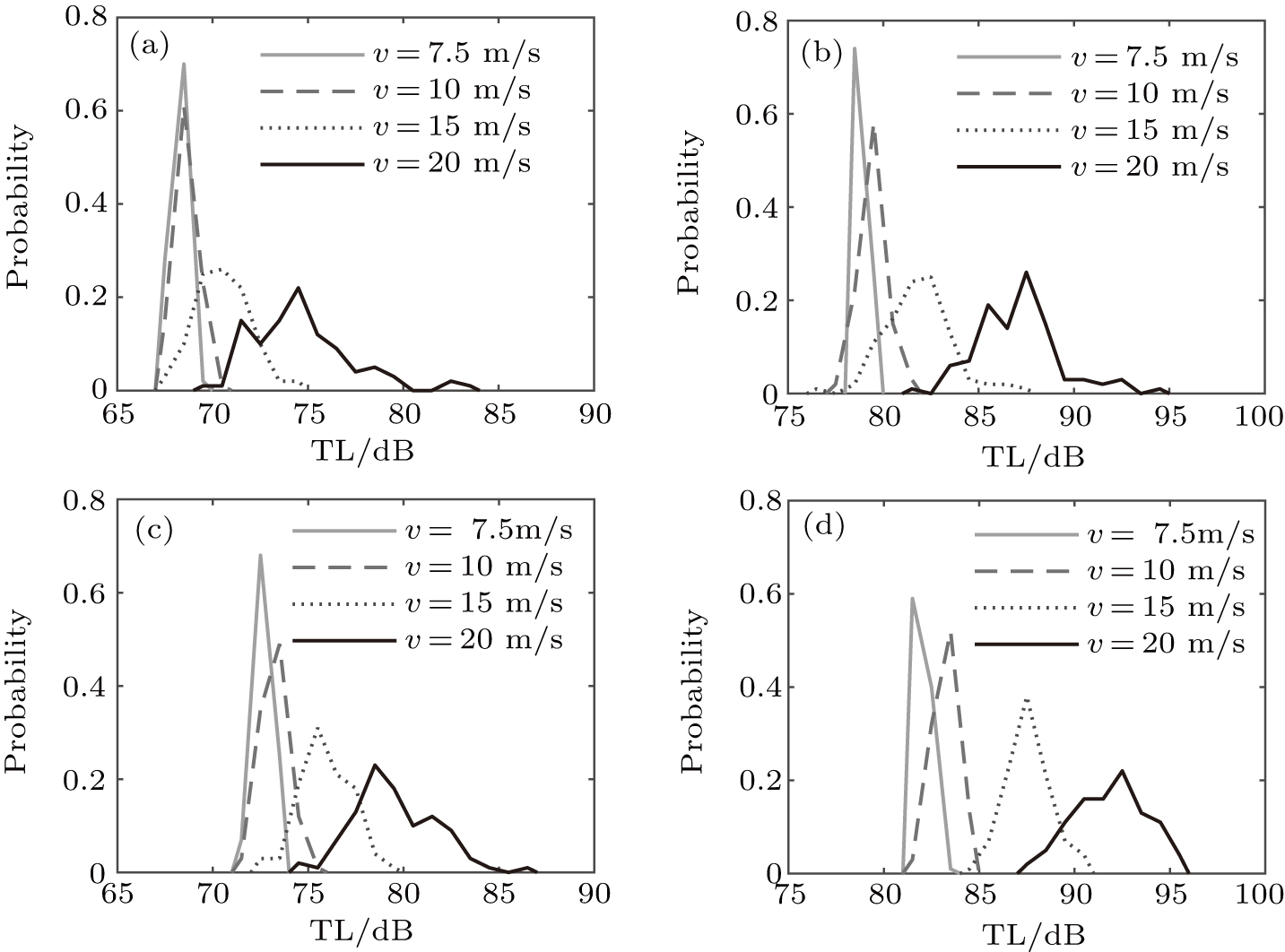
To investigate the regulation of TL distribution under the rough surface, simulation is conducted for four different wind speeds (v = 7.5 m/s, 10 m/s, 15 m/s, and 20 m/s) respectively, corresponding to four, five, seven, and eight wind scales. A set of 100 randomly fluctuating surfaces of each wind speed are separately generated by the wind-wave spectrum. The sound field under each set of surfaces is calculated and the result is obtained by averaging the energy of 10 frequencies within 1/3 octave bandwidth, according to Eq. (
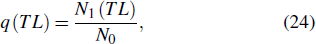 |
In Fig.
In Fig.
Compared with the case of 200 Hz at 20 km in Fig.
From the comparison between Figs.
Besides the TL caused by rough surface TLs, the TL caused by volume attenuation TLw also increases with frequency. The TL of the receiver depth, 10 m, is use to evaluate TLs
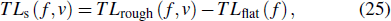 |
 |
The simulation results in this isothermal environment indicate that the statistical characteristics of TL is affected by the wind speed, range, and frequency.
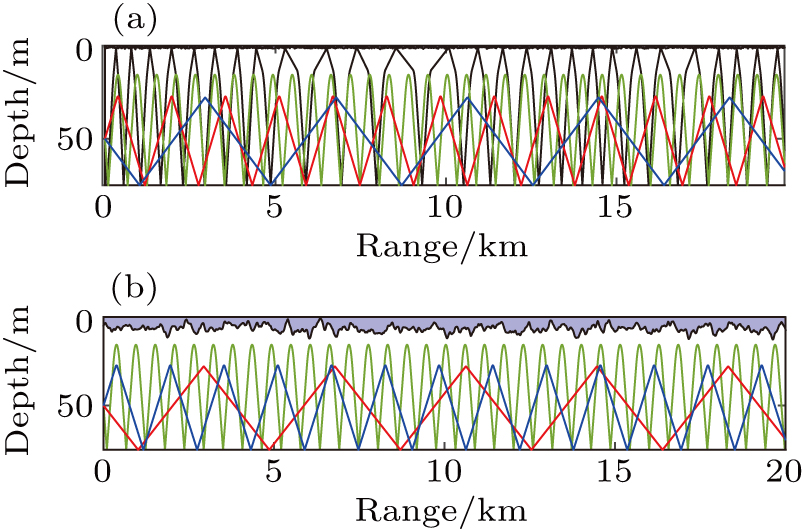
There is a typical waveguide with negative thermocline layer from the Yellow Sea experiment in 1996,[25] of which the environment parameters are shown in Fig.
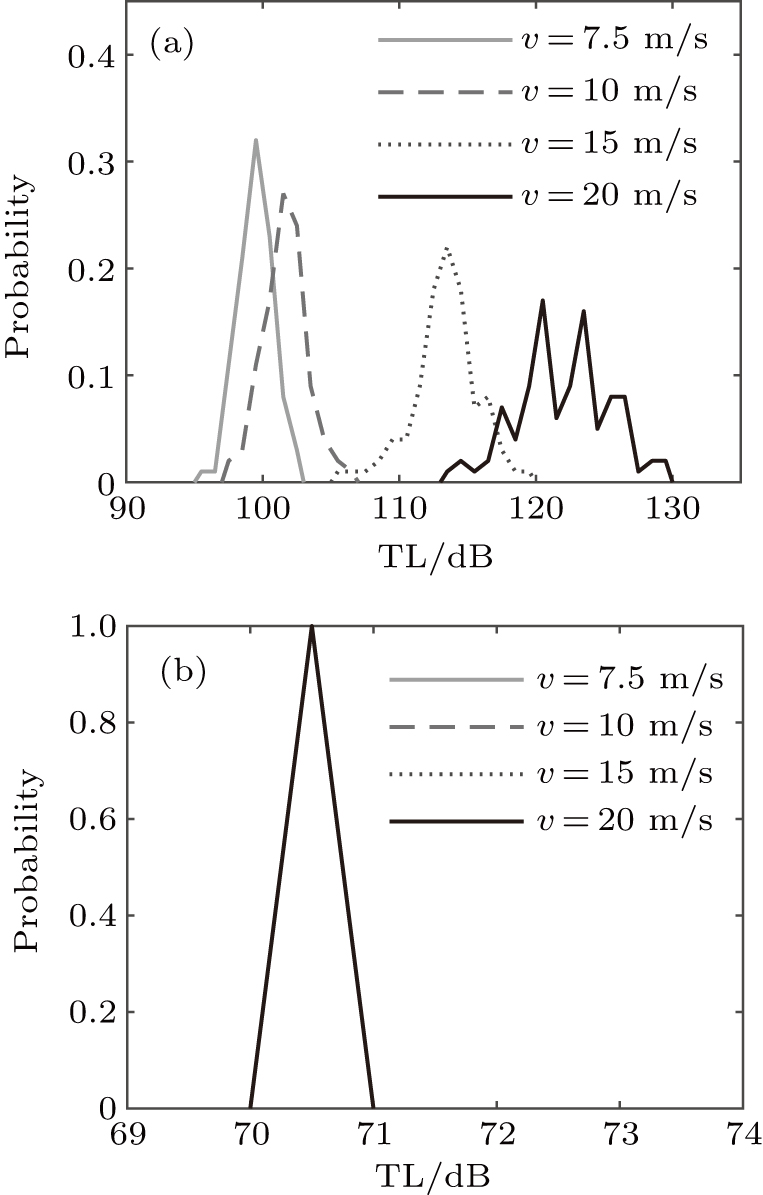
Figure
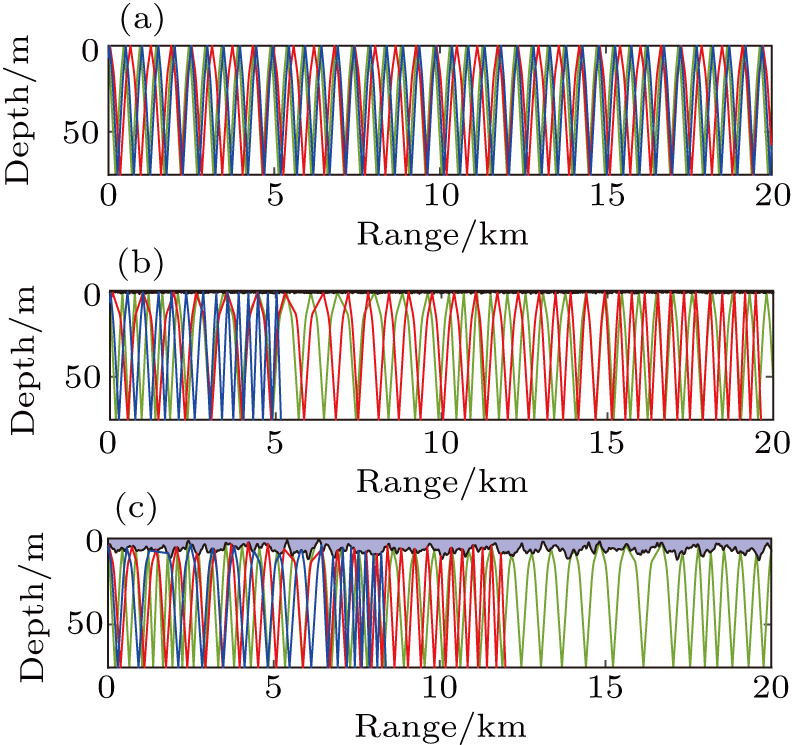 | Fig. 10. Rays for source above the thermocline (Zs = 7 m) with wind speeds of (a) 0 m/s, (b) 7.5 m/s, and (c) 20 m/s. |
In Fig.
Under a randomly fluctuating surface, a sound field in shallow water attenuates and randomly distributes in an interval. The simulations indicate that the statistical characteristics of TL are affected by the wind speed, range, frequency, and sound speed profile. Source and receiver depths relative to the thermocline are influential as well.
The TL is increasing and more dispersive as the wind speed raises due to the roughness of the surface. The increase is more significant for the higher frequency case due to the relative roughness of the surface. The interaction strength with the surface accounts for the following two phenomena. The TL increase with wind speed is more significant for the receiver farther away from the source. For the case of the source below the thermocline, the TL for the receiver below the thermocline is barely influenced by rough surfaces. While the TL for the source above the thermocline is more affected than that in an isothermal environment, because the grazing angle increases in the thermocline. In conclusion, the influencing factors are the relative roughness of the surface, the interaction strength of the sound field with the surface, and the changes of propagating angle due to refraction.
Besides, a reliable and rapid approach is introduced to simulate the distribution of TL under randomly rough surface environment. It can be used to evaluate the average value and the variation of TL under different wind-wave conditions. The regulations and the approach discussed in this paper is expected to be helpful for other underwater acoustic studies, such as sound field fluctuation with the presence of internal waves.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |