Project supported by the Slovak Research and Development Agency (Grant Nos. APVV-17-0501 and APVV-17-0522) and the Slovak Grant Agency for Science (Grants No. 1/0776/15).
Project supported by the Slovak Research and Development Agency (Grant Nos. APVV-17-0501 and APVV-17-0522) and the Slovak Grant Agency for Science (Grants No. 1/0776/15).
† Corresponding author. E-mail:
Project supported by the Slovak Research and Development Agency (Grant Nos. APVV-17-0501 and APVV-17-0522) and the Slovak Grant Agency for Science (Grants No. 1/0776/15).
We report properties of contact resistances observed on pentacene organic field-effect transistors (OFET) with four different source/drain electrodes, namely, copper (Cu), gold (Au), silver (Ag), and germanium (Ge). The metals were selected to provide a wide range of energy barriers for charge injection, from blocking contact to smooth injection. All OFETs exhibited strong voltage dependence of the contact resistance, even for devices with smooth injection, which is in strong disagreement with the definition of ohmic contacts. A comparison with current crowding, resistive network, Fowler–Nordheim tunneling, and electric field enhanced thermionic injection (Schottky emission) pointed to importance of local electric fields and/or electrostatic field charges.
Since the first organic field-effect transistor (OFET) was successfully demonstrated in the 1980s,[1,2] OFET devices have been used for the fundamental study of charge behavior in organic semiconductors, and also for promising applications. In the last three decades, a huge amount of progress in organic semiconductor synthesis has brought novel materials with properties such as air stability, low-cost synthesis, solubility, and high charge mobility. Meanwhile, device physics and electronics research has mostly concentrated on the fabrication technology, downscaling of devices to reach high device density, high output current, and fast switching speed.[3–5]
As the channel length becomes shorter, the charge transport through the device is even more affected by the injection properties and the electrode–organic semiconductor interface has become increasingly important. In other words, the short-channel devices exhibit significantly lower effective mobility due to potential drop on the injection electrode. The charge behavior on the electrode–organic semiconductor interface has been identified as a bottleneck of advanced OFET devices and an investigation of the underlaying physics has been envisioned as essential to obtain smooth injection.[6–14] The potential drop on an injection electrode is usually represented by the contact resistance as an important figure of merit for contacts. In addition, the contact resistance, which is an element of electrical equivalent circuit, is also a powerful tool for circuit design and modeling.[15,16] However, it has a deep physical meaning and many possible origins of the energy barrier have been proposed, such as energy level mismatch between the Fermi level of the injection electrode and the highest occupied molecular orbital (HOMO) level of an organic semiconductor with p-type conductivity, interfacial energy states, interfacial dipoles, mirror charge, internal electric field generated by traps, and so on.[17,18] Furthermore, the contact resistance has been found to be affected by many parameters, such as the gate insulator,[19] metal deposition rate of the injection electrodes,[20–22] injection electrode geometry,[23,24] or charge transport through channel.[25]
The charge injection on metal–semiconductor interface is a complex problem. There are a couple of charge injection processes that can take place, such as direct tunneling, Fowler–Nordheim tunneling, hopping through interfacial states, or electric-field enhanced thermionic emission (i.e., the Schottky effect).[6,26] The physics of inorganic semiconductor devices in accordance to the charge injection recognizes two fundamental kinds of contacts: (i) Schottky contacts and (ii) ohmic contacts.[27] The Schottky contacts provide rectifying behavior, often exhibit high contact resistance, and the charge injection is ruled by the electric-field enhanced thermionic emission. The requirement for ohmic contacts with low contact resistance is a common reduction of the definition because the most important property of ohmic contacts is their non-rectifying behavior (i.e., linear current–voltage, I–V, dependence). Consequently, the ohmic nature of contacts of OFET devices has often been verified by the linearity of the output current characteristics in low-voltage region.[28–31] However, the definition of the ohmic contacts through the contact resistance Rc as
 |
The present work is focused on OFET devices with pentacene as an organic semiconductor and several metals are used for source/drain contacts. The contact resistance is evaluated by the transmission line method (TLM) for various gate–source voltages and the voltage dependence is analyzed. We show that the metals that are generally assumed to be suitable for ohmic contacts of pentacene OFETs provide low contact resistance but not ohmic behavior. In addition, the voltage dependence is compared with several microscopic and macroscopic models to find the most suitable explanation.
In this study, OFET devices with top-contact bottom-gate geometry were fabricated using silicon wafers with 110 nm thermally grown silicon dioxide (SiO2) layer as the substrates. The substrates were cleaned in an ultrasonic bath subsequently by 20 vol.% ethanolamine aqueous solution, acetone, isopropyl alcohol, and in deionized water prior to further processing. Poly(methyl methacrylate) (PMMA, Sigma-Aldrich) was dissolved in toluene (Sigma-Aldrich) with a concentration of 3 wt.%. The PMMA solution was sonicated for 30 min and subsequently filtered through 0.22 μm sized polytetra fluoroethylene (PTFE) filter to remove insoluble particles. The solutions of PMMA were spun on to the substrates at 3000 rpm for 30 s and the prepared films were subsequently annealed at 160 °C for 90 min in ambient atmosphere to remove residual solvent prior the deposition of semiconducting layer. The PMMA film thickness estimated by Dektak 150 (Bruker, USA) mechanical profilometer was 70 nm. Consequently, the heavily-doped conductive Si wafers served as a gate electrode, whereas a gate dielectric layer was the PMMA/SiO2 bilayer. Then, a 100 nm-thick pentacene layer was thermally evaporated in vacuum with pressure lower than 10−4 Pa with fixed deposition rate of 2.4 nm/min. After the deposition of the semiconducting pentacene layer, selected metal was thermally evaporated through the shadow mask to form source and drain electrodes. Here, we used four different metals (Au, Ag, Cu, Ge) for the source/drain electrodes. The OFET devices had channel lengths L and width W of 50–200 μm and 2.5 mm, respectively. The structure of the fabricated OFETs is depicted in Fig.
The output and transfer characteristics of the fabricated devices with four different injection electrode metals are presented in Figs.
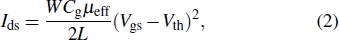 |
| Table 1. List of mobility values of of OFET devices using various metals for source/drain electrodes. The effective value was extracted by Eq. ( |
Given that the devices differ by the injection electrode only, the different effective mobilities should obviously originate in the injection barrier at the metal–organic semiconductor interface. Cu and Au are well known for smooth hole injection to pentacene, whereas Ag was reported to have a considerable energy barrier for holes.[34–36] Obviously, the device with Ge electrodes exhibits significantly lower effective mobility. Since the effective mobility is evaluated for an ideal OFET with smooth injection, the suppression of the effective mobility represents the effect of energy barrier on injected charge carriers. In other words, the contact resistance reduces the effective mobility. Meanwhile, the output characteristics in linear region (i.e., |Vds| ≪ |Vgs − Vth|) show a linear relationship between the applied voltage and output current for all injection electrodes, see Fig.
The ohmic contact as defined by Eq. (
 |
 | Fig. 3. Transmission-line method analysis of the OFET devices using various metals for source/drain electrodes under applied gate–source voltages of −20 V, −30 V, and −40 V. |
Figure
Current crowding in organic electronics is a well-accepted phenomenon in sandwich structures such as OLED devices,[43] it has also been suggested for OFET devices.[12] Although there is a huge overlap of the source and gate electrodes, in the steady state only the electrode’s edge contributes to the charge injection. Hence, the injection process is a balance between the organic semiconductor resistance in the channel region and the metal contact resistivity. Consequently, the charge is injected from an effective area that is defined as a product of the channel width W and the transfer length LT (the characteristic injection length).[12,23,44,45] The contact resistance in the current crowding model is ruled by the carrier concentration and follows[12]
 |
Another macroscopic model is the resistive network[9] using circuit theory concepts, where we break the problem into small parts so that the circuit element dimensions will be infinitesimal small. In other words, the injection electrode region can be divided into infinitely small slices, and the contact resistance of each slice is represented by distributed parameters (units per unit of length). Subsequent integration leads to the contact resistance
 |
There are several microscopic models for the metal/organic semiconductor interface. However, direct tunneling will be not discussed in detail here because it is a voltage independent contact resistance and causes ohmic behavior of contacts. The so-called Fowler–Nordheim tunneling is common for applied voltages V higher than energy barrier height ΦB (V > ΦB/e, where e is the elementary charge) and is characterized by the current–voltage dependence
 |
 |
The electric field-enhanced thermionic injection is also known as the Schottky emission. Briefly, the height of the potential barrier is lowered due to the combination of the applied electric field and the image force. The current through the metal/organic semiconductor interface is expressed by the thermionic emission (Schottky) current ISch enhanced by the electric field E as follows:
 |
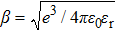
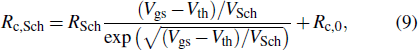 |
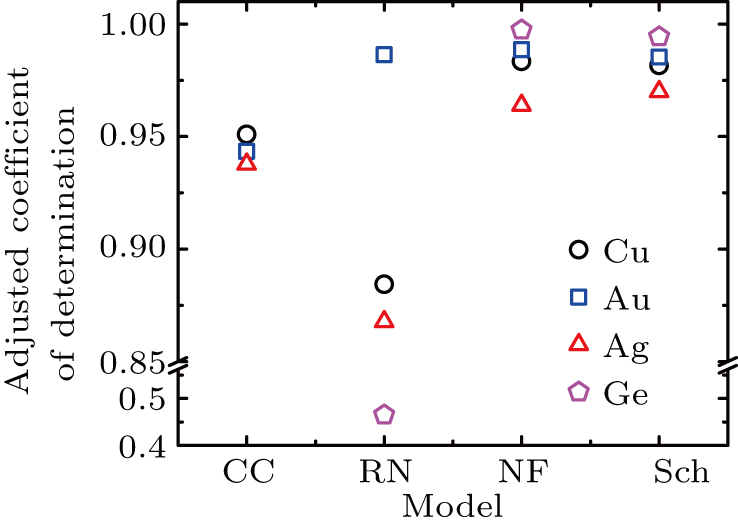
Obviously, the macroscopic models such as current crowding and resistive network cannot follow the voltage dependence of the contact resistances sufficiently, whereas the microscopic levels are in good agreement with the experimental results. The precision of the fit is evaluated using the adjusted coefficient of determination as depicted in Fig.
We have reported the voltage dependences of contact resistances observed on pentacene OFET devices with four different source/drain electrodes, namely, Cu, Au, Ag, and Ge. The metals selected for the electrodes provide a wide range of energy barriers for charge injection to give us a chance to investigate low and high contact resistances. All of the fabricated devices exhibited strong voltage dependence of the contact resistance, which is in disagreement with the definition of ohmic contacts. A detailed comparison with macroscopic and microscopic models for the voltage dependence of the contact resistance has revealed the possibility of Fowler–Nordheim tunneling and electric field enhanced thermionic injection (Schottky emission). Hence, even though we are able to reach relatively low contact resistance, there is no ohmic contact at all.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |