The past years have witnessed a continuous and stimulating progress in the study of superconducting quantum computing and quantum simulation in which the number of quantum bit (qubit) on a chip is increasing.^[1,2] In the multiqubit architecture, an amplifier with wide bandwidth is necessary to enable simultaneous readout of the quantum states of multiple qubits with single-shot sensitivity in the low-power dispersive measurement via superconducting microwave resonators coupled to the qubits.^[3,4] Josephson parametric amplifiers (JPAs)^[5] are often used as such device before the high electron mobility transistor (HEMT) amplifiers, which usually have noise temperature of 2 K–5 K in qubit working range, more than 10–40 times of single photon energy in the readout transmission line.^[6] Single-shot readout of the superconducting qubit states has been realized using JPAs of both the narrowband and broadband versions having bandwidths of a few tens^[7–9] and a few hundreds^[9–11] of MHz, respectively.

The operation of a JPA is based on the principle that the incoming signal photons are mixed with an applied pump tone via intrinsic nonlinearity of Josephson junctions, by which energy from the pump is converted into signal photons, thus providing an effective gain. To increase the amplification bandwidth of the JPA from narrowband to broadband, a common practice is to insert an impedance transformer between the narrowband JPA and the circulator (50-Ω environment) via which the signal to be measured comes to the JPA, and is amplified and reflected out to the HEMT for further amplification. There are two versions of the impedance transformer: One is the combined λ/4 and λ/2 transformer,^[10] the other is to use a tapered impedance transformer formed by a long co-planar waveguide (CPW) covered by density-varied crossovers.^[11] The latter, which is usually called impedance-transformed parametric amplifier (IMPA), has been used and reported in many studies.^[12–16]

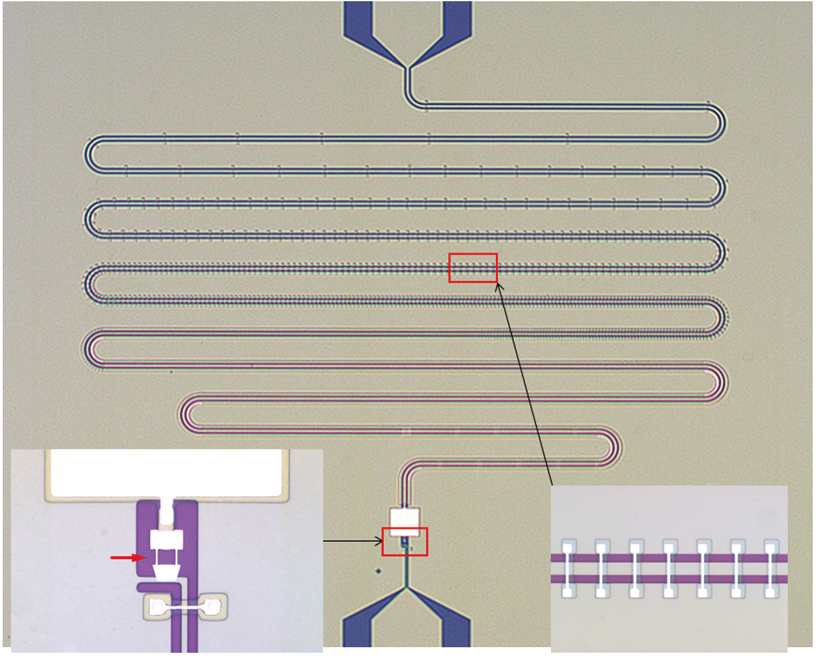
In this work, we present a study of IMPA and develop a fabrication process that is convenient and efficient for the device preparation. We use the Nb film for the bottom layer which contains the CPW and part of lumped-element style superconducting quantum interference device (SQUID) loop and shunt capacitor, as well as the SQUID bias circuitry. This offers several advantages as compared to the previous works in which Al films are used for the bottom layer.^[7–11] The Nb layer is patterned by direct writing by laser and reactive ion etching, followed by thermal evaporation of the CaF₂ insulating film and double-angle evaporation of the Josephson junctions.^[17,18] The IMPAs are then characterized systematically, which demonstrate a gain above 15 dB with a bandwidth as large as 600 MHz and the noise level approaching the quantum limit, thus the device is suitable for the applications with multiqubit purpose with the qubit number up to thirty expectedly. Finally, the IMPAs are tested with quantum state readout of an Xmon qubit. Our results show that the signal-to-noise ratio (SNR)^[8,19] and the qubit state readout fidelity^[12] are significantly improved by using the IMPA.

In Fig. 1, we show the false-colored optical photograph of the IMPA studied in this work with a design similar to that in Ref. [11]. The IMPA consists of a CPW covered with density varied crossovers as impedance transformer, part of which is shown in the right inset, a square-shaped planar shunt capacitor, and a dc SQUID with flux bias line. The two Josephson junctions locate in the middle of the two thin lines as pointed at by an arrow in the left inset. The shunt capacitor and the normal-state resistance of a single junction have the design parameters of 5.4 pF and 96 Ω–110 Ω, respectively. As can be seen in the figure, the device is made up of five film layers: The Nb base layer, the CaF₂ insulating layer, the Al film for the capacitor top electrode and crossovers, and two Al layers forming the Josephson junctions by the shadow evaporation. Although the capacitor top electrode and crossovers can also be fabricated in a single step together with the shadow evaporation of the junctions, we describe below the detailed fabrication process of the device considering they are prepared in the separate steps.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. False-colored optical photograph of the IMPA fabricated in this work. The IMPA consists of a long CPW covered with density varied crossovers, part of which is shown in the right inset, a planar shunt capacitor, and a dc SQUID with flux bias line. The two Josephson junctions locate in the middle of the two thin lines as pointed at by an arrow in the left inset. The width of the sample area shown in the main panel is 3 mm while the length of the crossover strips in the insets is about 35 μm.

In the present experiment, we used thermally oxidized high resistivity silicon substrates with specific resistance greater than 5000 Ω⋅cm. The substrates had a thickness of 0.45 mm with the oxidized layer thickness around 500 nm. The substrates were cleaned sequentially in an ultrasonic bath using acetone and isopropyl alcohol. They were treated at the temperature of 100 °C for 2 hours before being sent into an ultra high vacuum system for Nb film sputtering. The sputter system had a background pressure of 2 × 10⁻⁶ Pa, and Ar gas with purity > 0.9999 and working pressure of 1.5 Pa were used for sputtering. The substrate holder was water cooled so that the sample temperature was kept below 100 °C during sputtering. The sputtering voltage and current were 260 V and 0.45 A, respectively, which gave rise to a film deposition rate of 2.7 nm/s. We used 150-nm thick Nb film for the device bottom layer. The film was then photolithographically patterned using S-1813 resist (1300 nm in thickness) and direct writing by laser (DWL), and dry etched via reactive ion etching (RIE) in SF₆, which could be easily controlled compared to the Al film patterning used previously. Subsequently, the resist was removed in acetone and also in a microwave plasma system for the further cleaning of the residuals.

We used thermally evaporated CaF₂ film for the insulating layer in the IMPA, which could be conveniently patterned via the lift-off technique, instead of the α-Si film prepared by plasma enhanced chemical vapor deposition.^[20] For this we prepared LOR2A/S-1813 (200 nm + 1300 nm) resist double layer. A 200-nm thick LOR2A layer was first spin coated and baked up at 170 °C for 1 minute. A 1300-nm thick S-1813 layer was coated afterward and baked up at 115 °C for 1 minute. The double layer was exposed in the DWL system with the power of 60 W. It was developed at 24 °C for 75 s and fixed for 30 s. Then a 130-nm thick CaF₂ film was evaporated in a thermal evaporation system and lifted off, which completed the insulating layer for the capacitor and crossover, etc. The Al layer for the top electrode of the capacitor and crossovers were fabricated subsequently using the lift-off process with single S-1813 resist layer patterned via DWL.

In the final step, shadow evaporated Josephson junctions for the SQUID were prepared in a Plassys system (Plasyss 520) to complete the fabrication of IMPA. Similar conditions to those in our previous work^[18] were used for the MAA/PMMA double resist layer preparation for the lift-off process and a pre-cleaning in O₂/Ar mixing gases was performed. Different from other reported works, we used the Nb film for the base layer so it was not required to prepare in a separate step the Au film position marks for the e-beam lithography,^[9,18] which therefore simplified the sample fabrication process. The Nb film also had better mechanical strength which allowed for repeated bonding of the device in the sample box if required.

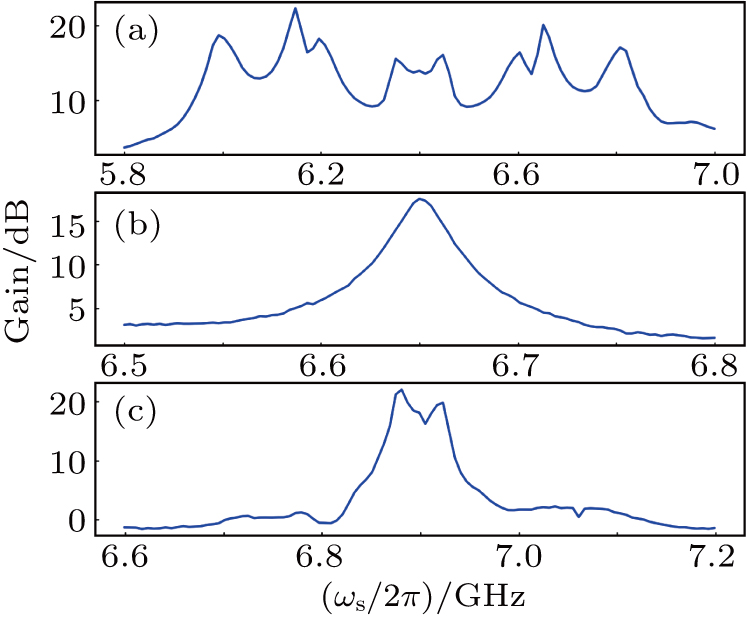
Below we present our experimental results of the fabricated IMPA, which can be roughly divided into two parts: Characterization of the device to find its optimized working parameters and test of the signal amplification with a qubit. As is shown in Fig. 2, for the device characterization there are five parameters to be considered: The dc bias I_b for the SQUID critical current modulation, the pump tone ω_p and power P, and those of the incoming signal ω_s and P_s. In our experiment, we first chose a central frequency ω₀/2π and the frequency of the pump ω_p/2π was set around 2ω₀/2π (e.g., ω_p = 2ω₀ ± 2π × 2 MHz). Also a fixed moderate power P_s of the incoming signal was used first. With these we could adjust three parameters I_b, P, and ω_s to optimize the IMPA performance in terms of its gain, bandwidth, system noise temperature, and the saturation power.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Circuit diagram of the IMPA with its surrounding accessories. The circulator on the left is used to separate the incoming and amplified outgoing signals. There is a coaxial cable with length L connecting the circulator on one side and the IMPA via wire bonding on the other. On the right side of the IMPA there is a bias tee to combine the dc bias and rf pump for driving the IMPA.

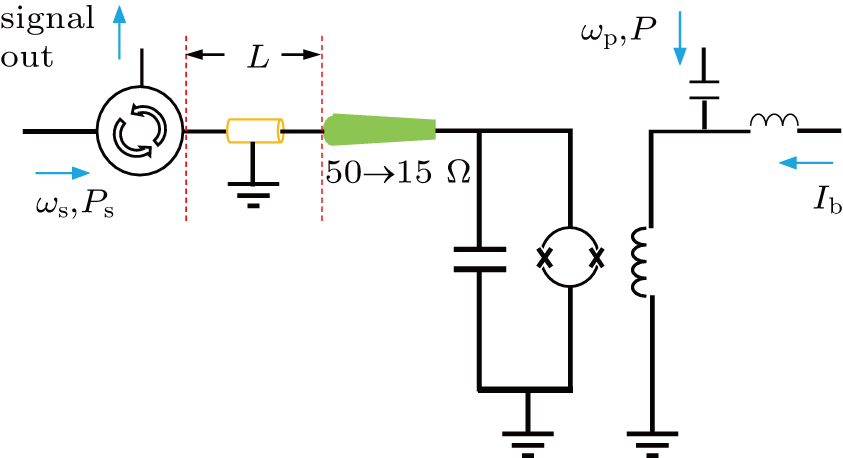
For the measurement of the IMPA, the device was bonded in a copper sample box which was mounted in a cryogen-free dilution refrigerator with standard electronic circuitry for the dispersive readout of transmon or Xmon qubits. The IMPA was connected to the qubit readout transmission line via a circulator as shown on the left side in Fig. 2 and the output signal was further amplified by an HEMT. Figure 3 shows the reflected phase of the low-power signal versus the dc flux bias I_b and signal frequency ω_s/2π, where a periodic structure is observed due to the change of the SQUID critical current with the external magnetic flux. The measurement is performed by setting the signal power to P_s = −116 dBm. The result is seen to be shifted horizontally by a small amount and centered around an I_b slightly larger than 0.2 mA due to flux trapping in the SQUID loop. There are clear borders (zero phase) across which the reflected phase changes sign. These borders, appearing wavy due to the impedance transformer, follow basically the modulation curve of the SQUID. We can therefore tune the resonant frequency into the regime for the qubit readout by changing I_b.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Reflected phase of the low-power signal versus the dc flux bias Ib and signal frequency ωs/2π. The periodic structure can be seen with clear borders (zero phase) across which the reflected phase changes from plus to minus, or vice versa.

To optimize the working parameters of IMPA we start with the measurement of the gain when an input signal is sent to the qubit readout transmission line which is connected to the signal port on the left side in Fig. 2. The gain is defined as the ratio of the output signal amplitude to that of the input signal when pumping of IMPA is on and off. In Fig. 4(a), we show the gain under the variations of the pumping power P and dc bias I_b. The result is measured by setting ω_p = 2ω₀ + 2π × 2 MHz and ω_s = ω₀ with the frequency ω₀/2π = 6.3 GHz and the range of I_b chosen by considering the result in Fig. 3. In Fig. 4(a), we see that there are two regions in which the gain reaches the level of 20 dB. Now we show two typical results demonstrating the quantum-limited performance of the the present device for the measurement of the qubit states.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The gain of the IMPA under the variations of the pumping power P and dc bias Ib (a) and under the variations of the pumping power P and the signal frequency ωs/2π (b). The color bars indicate the gains in unit dB. The left and right white dots in panel (a) indicate the two parameter sets for the results shown in Fig. 5. See text for the parameters used in the measurements.

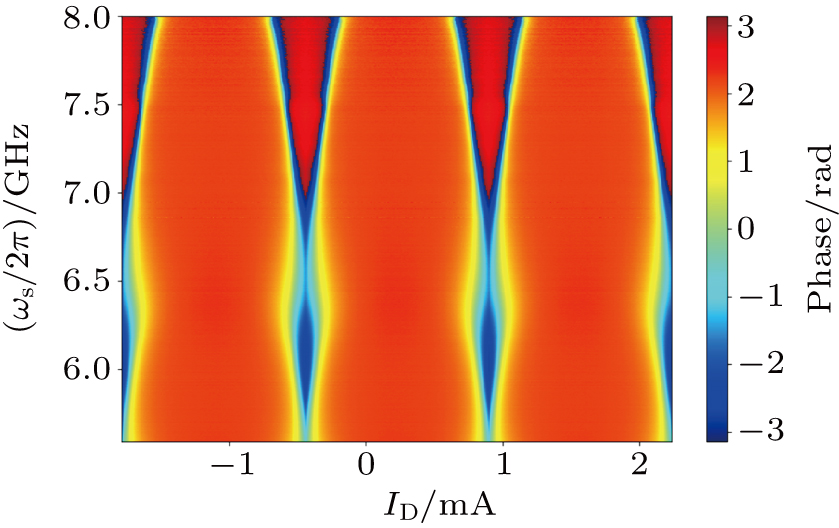
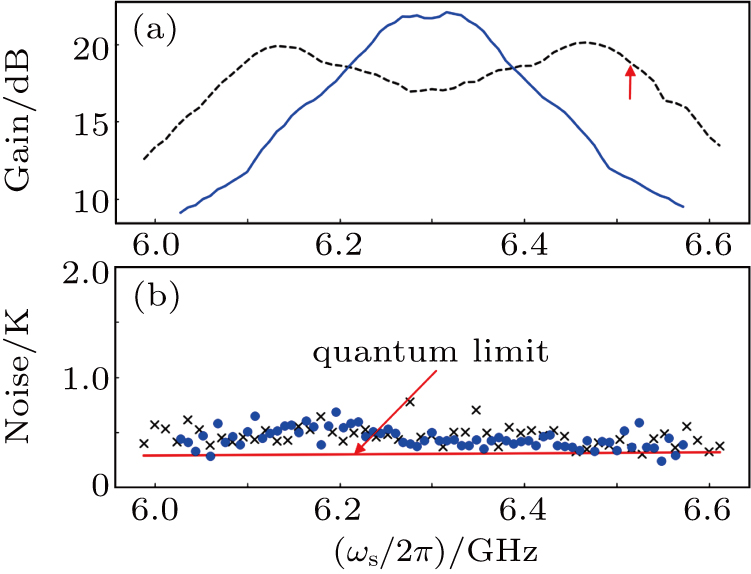
We first set I_b = −0.055 mA and measure the gain under the variations of the pumping power P and the signal frequency ω_s/2π with the other parameters unchanged. The result is plotted in Fig. 4(b), which shows that near P ∼ −33 dBm, there is a narrow frequency range where the gain goes well above 20 dB. As P increases, the gain gradually decreases while the frequency range is broadened over which the gain remains significant. Based upon this result, we are able to choose a power P at which both the gain and the frequency range, or the bandwidth, are sufficient for the multiqubit measurement.^[10]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The signal frequency dependence of the gain (a) and noise (b). Solid line and dots: Ib = −0.055 mA, P = −31.9 dBm; dashed line and crosses: Ib = 0.54 mA, P = −32.5 dBm. The two parameter sets are indicated in Fig. 4(a) as left and right white dots, respectively, with the other parameters used in the figure unchanged.

In Fig. 5(a), we show the gain profile versus the signal frequency obtained with the power of the pump tone P = −31.9 dBm (solid line), represented by the left white dot in Fig. 4(a). We can see that the IMPA has 300-MHz wide frequency range over which the gain is greater than 15 dB. In Fig. 5(b), we plot the device noise against signal frequency (dots) together with the quantum limit (line) which is defined as one photon energy of total system noise at the input of the IMPA.^[7,11] The device noise is calculated using the approach of SNR improvement over the calibrated noise of the HEMT amplifier,^[5,7,11] It can be seen that the system noise is approaching the quantum limit over the bandwidth of 300 MHz.

A wider bandwidth of nearly 600 MHz over which the gain is above 15 dB is also achieved, as shown in Fig. 5 as a dashed line and crosses, respectively. The results are measured with I_b = 0.54 mA and P = −32.5 dBm, as indicated by the right white dot in Fig. 4(a). In the multiqubit experiment, the frequency separation between any two qubit readout resonators should not be too small in order to have an effective state differentiation during readout. Assuming a minimum separation of 20 MHz, the present IMPA allows for a single-shot simultaneous state readout of a 30-qubit system considering the bandwidth of 600 MHz.

So far the measurements are performed with a fixed signal power of P_s = −116 dBm. By changing P_s and using the parameters in the above experiment, we measure the gain and noise temperature against P_s from −95 dBm down to −135 dBm. It is found that for the gain around 18 dB it basically remains unchanged from −135 dBm up to −115 dBm and starts decreasing noticeably at about −110 dBm. If we define the saturation power as the 1-dB compression point in gain versus the signal power,^[7] our results indicate that the saturation power of the present IMPA is around −110 dBm, hence there exists a wide signal power range of the IMPA for the qubit quantum state measurement.

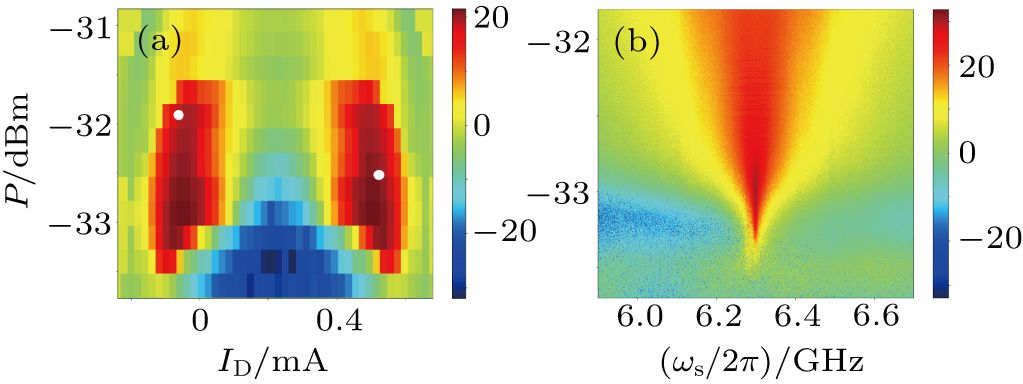
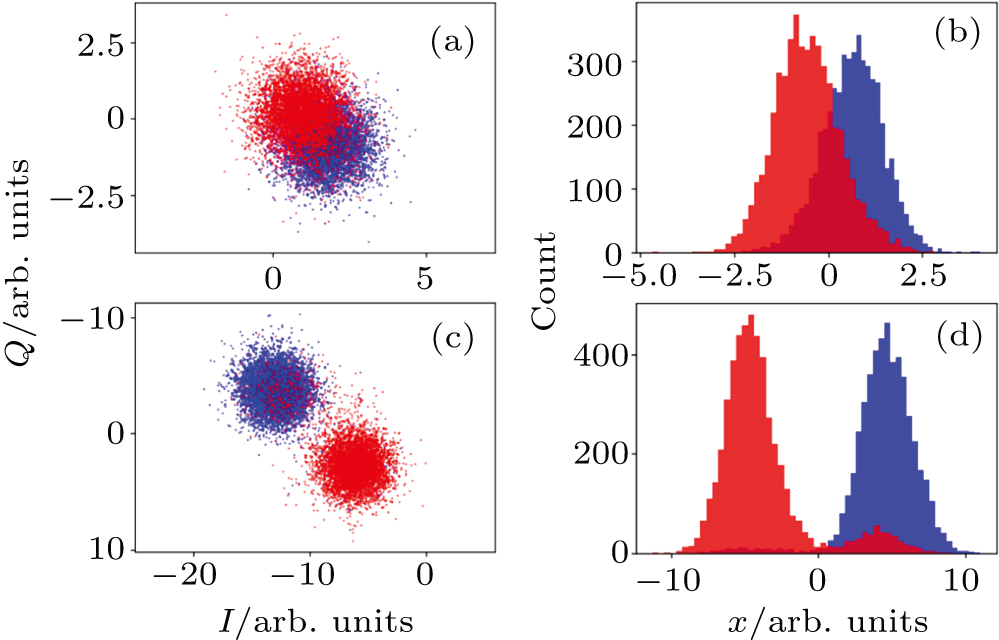
To test the performance of the IMPA, we use an Xmon qubit in an array of 10 coupled qubits with the |0〉 and |1〉 states level spacing of ω₁₀/2π = 4.701 GHz. The qubit has a T₁ ranging from 15 μs to 20 μs and a T_φ around 2 μs from the Ramsey interference measurement. The readout resonator has a frequency ω_r/2π = 6.515 GHz, a photon decay rate κ/2π = 628 kHz, and the frequency shift parameter χ/2π = 500 kHz that leads to a coupling strength of g/2π = 30 MHz with the qubit. The working parameters for the IMPA are those used in obtaining the result represented by the dashed line in Fig. 5(a), in which an upward arrow indicates the point having the signal frequency ω_s/2π = ω_r/2π and a gain about 19 dB. In our experiment, the measurement pulse with a duration of 1 μs is used, and the signal reflected and amplified from the IMPA is sent to an HEMT and two successive microwave amplifiers for further amplification before sending to an IQ mixer for demodulation. The demodulated signals are further amplified by an intermediate-frequency amplifier and recorded in the computer via analog-to-digital converter for readout analysis, from which the I and Q components are obtained.

In Fig. 6, we plot the I–Q results for the qubit |0〉 (blue) and |1〉 (red) states measured when the pump of the IMPA is off (a) and on (c). The separation of the blue and red data points appears much larger when the IMPA is on. In panels (b) and (d) we show the corresponding distribution histograms, in which the horizontal axes are defined along the directions from the center of the |1〉 state data to that of the |0〉 state data in panels (a) and (c). By using the Gaussian fit to the data, we are able to calculate SNR given by Ref. [8] S_0,1 = |x_0,1|/σ_0,1, where x_0,1 and σ_0,1 are the average values and standard deviations of the Gaussian fit when the qubit is in the |0〉 and |1〉 states. We find S₀ and S₁ to be 0.80 (3.16) and 0.62 (2.93) when pumping of the IMPA is off (on), which give rise to a factor of 3.95 and 4.73 increase in SNR for the qubit in the |0〉 and |1〉 states (In some works, SNR is defined by Ref. [19]: S = (x₀ – x₁)²/2σ² where in many cases σ = σ₀ = σ₁. In the present experiment, if we set σ = (σ₀ + σ₁)/2, we arrive at S = 1.0 and S = 18.59 when pumping of the IMPA is off and on, respectively). As a result, the qubit |0〉 and |1〉 states readout fidelities are found to increase to above 97% and 91%, respectively, enabling therefore single-shot quantum state measurement for the multiqubit system. We note that the readout fidelities are comparable to those in the recent experiments^[14,16] in which IMPAs with similar design but with Al bottom layers are used.

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. Inphase-quadrature and histogram plots of the single-shot measurement of an Xmon qubit prepared in the |0〉 (blue) and |1〉 (red) states, performed with the pump of the IMPA off (a), (b) and on (c), (d). The horizontal axes in panels (b) and (d) are defined along the directions from the center of the |1〉 state cloud to that of the |0〉 state cloud in panels (a) and (c). Qubit |0〉 and |1〉 states measurement fidelities are above 97% and 91%, respectively.

Finally we mention that the above measurements are performed with sample box containing the IMPA connected directly onto the circulator, namely we have L = 0 (see Fig. 2). In our experiment, we have also studied the influence of the environment admittance on the IMPA performance by changing the length L of the cable between the device and the circulator thus changing the pattern of standing waves in the output line. In Fig. 7, we show the results at three central frequencies of ω₀/2π = 6.40, 6.65, and 6.90 GHz with L = 25 cm. These results extend the work in Ref. [11] in which the cases with L = 10 cm and 20 cm are examined. In the present case, we can see that there is clear multi-peak structure in Fig. 7(a), which has not been observed in the experiment with L = 0. There are also more peaks compared with the data in Ref. [11] with shorter L = 10 cm and 20 cm, as expected. Overall, we find in our experiment that the shorter the cable connecting the IMPA to the circulator, the better the IMPA performance will be.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Influence of the standing waves in the external environment obtained by adding a cable with length L = 25 cm that connects the IMPA to the circulator (see Fig. 2). The results are measured with three central frequencies ω0/2π of (a) 6.40 GHz, (b) 6.65 GHz, and (c) 6.90 GHz.

We have developed a fabrication process of the IMPA for the quantum state measurement in superconducting multiqubit applications. The process employed Nb film as the base layer, which proved convenient in sample patterning using e-beam lithography and dry etching. The Nb film also had good mechanical strength which allowed for repeated bonding of the device in the sample box. We then presented a systematic characterization of the IMPA. We showed that the JPA had a bandwidth up to 600 MHz with gain above 15 dB and noise temperature approaching the quantum limit. The qubit state differentiation measurements demonstrated an SNR increase by a factor of four and above when pumping of the IMPA was off and on, and the readout fidelity was found to rise to above 97% and 91% for the ground and first-excited states, respectively. The present IMPA can be used for the single-shot quantum state measurement of the multiqubit system with the qubit number up to around thirty.