Cite this Article
Wang Zhen-Hua, Gao Xuan P A, Zhang Zhi-Dong. Transport properties of doped Bi2Se3 and Bi2Te3 topological insulators and heterostructures. Chinese Physics B, 2018, 27(10): 107901  
Permissions
Transport properties of doped Bi2Se3 and Bi2Te3 topological insulators and heterostructures
Wang Zhen-Hua1, †, Gao Xuan P A2, Zhang Zhi-Dong1
Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China
Department of Physics, Case Western Reserve University, Cleveland, Ohio 44106, USA

 

† Corresponding author. E-mail: zhwang@imr.ac.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 51522104, 51590883, 51331006, and KJZD-EW-M05-3) and the National Science Foundation for its financial support under Award DMR-1151534.

Abstract
Abstract

In this review article, the recent experimental and theoretical research progress in Bi2Se3- and Bi2Te3-based topological insulators is presented, with a focus on the transport properties and modulation of the transport properties by doping with nonmagnetic and magnetic elements. The electrical transport properties are discussed for a few different types of topological insulator heterostructures, such as heterostructures formed by Bi2Se3- and Bi2Te3-based binary/ternary/quaternary compounds and superconductors, nonmagnetic and magnetic metals, or semiconductors.

PACS: 79.60.Jv;91.60.Tn;68.55.Ln;73.43.Qt
Keyword:transport properties;interfaces;heterostructures;nanostructures;doping;magnetoresistance
1. Introduction

Topological insulators (TIs) have received increasing attention because of their unique electronic structures, which generally have a gapped bulk band structure and a band inversion induced by spin-orbit interaction that leads to a metallic topological surface state. The recently discovered three-dimensional (3D) TIs show an unconventional electronic phase driven by strong spin–orbit interaction. TI has metallic Dirac fermion surface states that are protected by time-reversal symmetry, resulting in unique properties such as spin momentum locking and prohibited backscattering.[1] 3D TIs have the simplest surface states consisting of a single Dirac cone, which has been proposed theoretically in the stoichiometric compounds Bi2Se3, Bi2Te3, and Sb2Te3.[1] They share the same rhombohedral crystal structure with the space group D3d5 (R3m), with five atoms in the trigonal unit cell. The presence of Dirac states on the surface of 3D TIs has been confirmed by angle resolved photoemission spectroscopy (ARPES) and scanning tunneling microscopy (STM).[2] These surface states can also be probed by magneto-transport measurements. Numerous studies of magneto-transport measurements also have been performed to prove the existence of surface states by means of analyzing weak anti-localization (WAL) and Shubnikovde Has (SdH) oscillations in Bi2Te3 and Bi2Se3.[3] The WAL effect can serve as a convenient method for detecting decoupled surface transport in TI thin films. When a bulk Fermi surface coexists with the surface states, the low-field magneto-conductivity is well described by the Hikami–Larkin–Nagaoka equation. When the electron density is decreased, strong evidence is found for independent conducting channels at or near the bottom and top surfaces.[4] However, the contribution of surface state carriers is generally negligible compared with the transport in bulk because the bulk tends to have high intrinsic doping and is thus quite metallic.[5] Therefore, many methods have been explored to control the bulk transport and modulate the transport properties of TIs. For example, a very large tunability in carrier density with a back gate was observed in Bi2Se3 thin films. The observed low-field magneto-conductivity resulting from WAL had a gate-voltage dependence when the electron density was reduced to very low values by gating.[6] The bulk properties and WAL effect of Bi2Se3 films exhibited thickness dependences over a range of up to five orders of magnitude in thickness.[7] The electronic transport in charge density-tunable microdevices patterned from thin films of TI Bi2Se3 has also been studied. These devices exhibited pronounced electric field gating effects, including ambipolar modulation of the resistance.[8] A brief summary of the history of topological insulators and transport experiments on TI films and nanowires can be found in related review papers.[9,10]

In this manuscript, we review the recent experimental and theoretical research efforts in Bi2Se3- and Bi2Te3-based TIs to achieve control of the Fermi energy (e.g., tuning the Fermi energy into the bulk band gap) by synthesizing ternary/quaternary compounds, gating, or doping with nonmagnetic and magnetic elements. We also discuss some of the fascinating properties of these modified TIs and various heterostructures based on TIs.

2. Transport properties of TIs modulated by doping
2.1. Doping TIs with magnetic elements

TIs having magnetic ordering have recently attracted interest because of their promising applications in spintronics and many other novel phenomena, such as the magnetic monopole, novel magnetoelectric quantum states, and quantum anomalous Hall effect (QAH) proposed in ferromagnetic TIs.[11,12] The ferromagnetism introduced by magnetic impurities in a TI film can induce a gap in the Dirac surface, making the TI a QAH insulator if the Fermi level lies in the gap. Magnetic dopants can break the time-reversal protection of the Dirac point, which may open up new applications.

Based on first-principles calculations, the tetradymite semiconductors Bi2Te3, Bi2Se3, and Sb2Te3 are predicted to form magnetically ordered insulator states when doped with transition metal elements (such as Cr or Fe).[11] Much effort has been spent to prepare TIs doped with transition metal elements. Flakes of Cr0.15(Bi0.1Sb0.9)1.85Te3 give strong ferromagnetic loops with a TC of ∼13 K. Anomalous Hall resistance is observed, indicating obvious suppression because of electron–phonon interactions.[13] Ferromagnetism is observed in TI Co0.08Bi1.92Se3 single crystals. However, the anomalous second ferromagnetic phase transition is indicated by the complicated ferromagnetic ordering below 30 K.[14] The magnetization coming from individual Co atoms deposited on the surface can disrupt the spin coherence of the carriers in the TI Bi2Te3 because of the hybridization of Co with the surface states, while in Bi2Se2Te, the spin texture remains unperturbed because of the Se–Te disorder of localized magnetic moments in the distorted adsorption geometry.[15] Fe-doped Bi2Se3 single nanowires give direct evidence of spontaneous magnetization, with a TC of ∼40 K.[16] Locally manipulating the electronic states of Fe dopants in Bi2Se3 crystals gives evidence that the specific impurity neighborhood and the position of the Fermi energy have to be taken into account when considering electron scattering from the disorder in TIs.[17] A single-phase crystal structure can be obtained for (CrxSb1−x)2Te3 with x up to 0.44, and composition analysis reveals that Cr replaces Sb. A ferromagnetic state with a TC ∼250 K in (Cr0.44Sb0.56)2Te3 films has been reported, which is the highest TC observed in magnetically doped TIs so far.[18] A systematic study of V-doped Bi2Se3 films reveals the crucial role of topological surface states in ferromagnetic coupling.[19]

The ferromagnetism order is achieved in TI, and the enhanced ferromagnetism with reduced carrier density can support the QAH phase in two-dimensional (2D) thin films of such systems. The QAH effect in Cr-doped topological insulators has been calculated, showing that Sb2Te3 is a better QAH-effect TI than Bi2Se3 or Bi2Te3.[20] It has also been proposed that Mo and Cr co-doping can enlarge the spin splitting of the topological surface states of Sb2Te3 and (Bi, Sb)2Te3, so that the QAHE can persist to higher temperatures. The temperature of the QAH effect also can be significantly increased by co-doping Cr and V magnetic elements in (Bi,Sb)2Te3 TIs.[21] The electric field has a strong effect on the magnetic order for Cr-doped Bi2(SexTe1−x)3 with the application of a gate voltage. Theoretical calculations show that the electronic energy level shift in a perpendicular electric field is due to the Stark effect,[22] so the best way to see the QAH effect in experiments is measuring the Hall conductance by tuning the chemical potential with the gate voltage. The hysteretic magneto-conductance has been investigated, and butterfly-shaped hysteresis characteristics are observed as the applied field increases. This hysteresis is attributed to the formation of gapless chiral domain wall bound states during a magnetic-field sweep. This phenomenon has also been studied theoretically, providing a link between microscopic magnetization dynamics and butterfly hysteresis.[23] The QAH effect is observed experimentally in magnetic thin films of Cr-doped (Bi,Sb)2Te3.[24,25] At zero magnetic field, the anomalous Hall resistance reaches the predicted quantized value by gate tuning, with an obvious drop in the longitudinal resistance. The longitudinal resistance vanishes under a strong magnetic field, whereas the Hall resistance remains at the quantized value. The experimental results illustrate a method to develop topological quantum electronic and spintronic devices by the realization of the QAH effect, which does not require a magnetic field.

2.2. Doping TIs with nonmagnetic elements

A 3D TI is a novel state of matter characterized by two-dimensional (2D) metallic Dirac states on its surface. However, the bulk has many native defects, such as the Se vacancy (VSe) and the Bi antisite (BiSe), which means that the bulk carriers from defects dominate over the surface electrons.[26] To verify the topological nature of the surface states, Bi-based chalcogenides such as Bi2Se3, Bi2Te3, Sb2Te3, and their combined/mixed compounds have been intensively studied, and some novel properties, such as the quantum Hall effect and superconductivity, have been reported.

Some effective methods to reduce the effect of bulk carriers on surface states include forming multicomponent compounds and gating.[27–33] The different kinds of defects at the surface of a (Bi0.53Sb0.47)2Te3 TI thin film have been analyzed, finding the largest localized voltage drop to be located at domain boundaries.[27] The quantum Hall effect on the surface Dirac states in (Bi1−xSbx)2Te3 films can be realized with electrostatic gate-tuning of the Fermi level in the bulk band gap under magnetic fields.[28] Resistivity anisotropy induced by an in-plane magnetic field has been observed in dual-gated bulk-insulating Bi2−xSbxTe3 thin films, which show a novel planar Hall effect from the TI surface.[29] The dominant charge carrier changed from n-type to p-type at approximately x = 0.7, indicating that the Fermi level can be controlled across the Dirac point. The ambipolar field effect from surface state conduction has been achieved in Bi2(Te1−xSex)3 nanoribbons by applying a back gate voltage.[30,31] Additionally, the helicity-dependent photocurrent in (Bi1−xSbx)2Te3 thin films has been studied synthetically, and the circular photo-galvanic effect has been identified as the dominant mechanism. Strong interlayer interference and coupling of bulk carriers with surface states are observed for all concentrations of Sb at low temperatures.[34,35] The optical properties of thin films of Bi2(Te1−xSex)3 have been investigated using a combination of infrared ellipsometry. The energy of the onset of direct interband transitions exhibits a maximum in Bi2Te2Se films, indicating the crossover of the direct interband transitions.[36] The linear magnetoresistance behavior has been shown to be a competition between the bulk insulating states and the metallic surface states.[37] Tuning the Landau levels of the Dirac cones in the top and bottom topological surface states independently can be realized in BiSbTeSe2 by employing both top- and back-gate electric fields at high magnetic field, forming charge puddles as a result of the strong Coulomb disorder.[32,33]

The surface state properties of TIs also can be improved by doping other elements, such as Ca, In, and Cu.[38–47] Few-layer crystals of Bi2Se3 have sufficiently low bulk carrier density after doping with Ca, which leads to gate voltage-tunable surface conduction.[38] A quantum phase transition from the topological to a trivial insulating phase is achieved in (Bi1−xInx)2Se3 film by In doping onto the Bi site.[39] Single-crystalline (Bi1−xInx)2Se3 shows quantum oscillations manifesting the nontrivial transport and high mobility.[40] Because of the topological phase transition-enhanced interface coupling near the topological critical point in (Bi0.92In0.08)2Se3, the in-plane negative magneto-resistance emerges and survives up to room temperature.[41] Recently, ARPES results indicated that Cu predominantly intercalates into the van der Waals gap when the Cu concentration is at low level, while with further doping, Cu can replace Bi, causing the saturation of the carrier concentration.[42] Cu can reduce the bulk carrier density of Bi2Se3 by compensating for native defects, such that the resistivity is changed from metallic to insulating-like behavior.[43–45] Moreover, Cu can intercalate in the van der Waals gaps between the Bi2Se3 layers, which has been investigated by Raman spectroscopy.[46,47] The peaks of Eg(2) and A1g(2) modes will shift to lower frequencies if Cu intercalates between the layers of Bi2Se3. However, the Eg(2) and A1g(2) modes are expected to shift to higher frequencies when Bi is substituted by Cu. As shown in Fig. 1(a), Eg(2) and A1g(2) mode peaks first shift to lower frequencies at low Cu concentrations, and then shift to higher frequencies with further increasing Cu concentration. This result indicates that Cu atoms occupy the intercalative sites between the layers at low Cu concentrations and take the substitutional sites of Bi atoms gradually with increasing Cu concentration. As shown in Fig. 1(b), an insulator–metal transition below ∼37 K is observed in CuxBi2Se3 films with increasing Cu concentration, which is due to electron delocalization resulting from strong hybridization between Cu+ and Cu2+ conduction bands.[47] When Cu intercalates into the van der Waals gap, it can donate as a Cu+ state, and the substituted Cu is in the Cu2+ state. Meanwhile, a relaxation behavior in the time dependence of resistivity is also observed because of the electron delocalization.[47] The temperature dependence of resistivity at zero magnetic field of CuxBi2Se3(x = 0.076) before and after relaxation at 2 K is shown in Fig. 1(c). The kink in resistivity at 37 K is more pronounced after stabilizing at low temperature for a long time, and the two resistivity curves show the same behavior above 37 K. As shown in Fig. 1(d), the resistivity relaxation process with time at 2 K has also been investigated. The red line is the fitting curve. In addition, the dependence of resistivity with time at 2 K for CuxBi2Se3 films with various Cu concentrations is shown in Fig. 1(e). As the Cu concentration increases, the relaxation rate E decreases; that is, relaxation becomes slower.

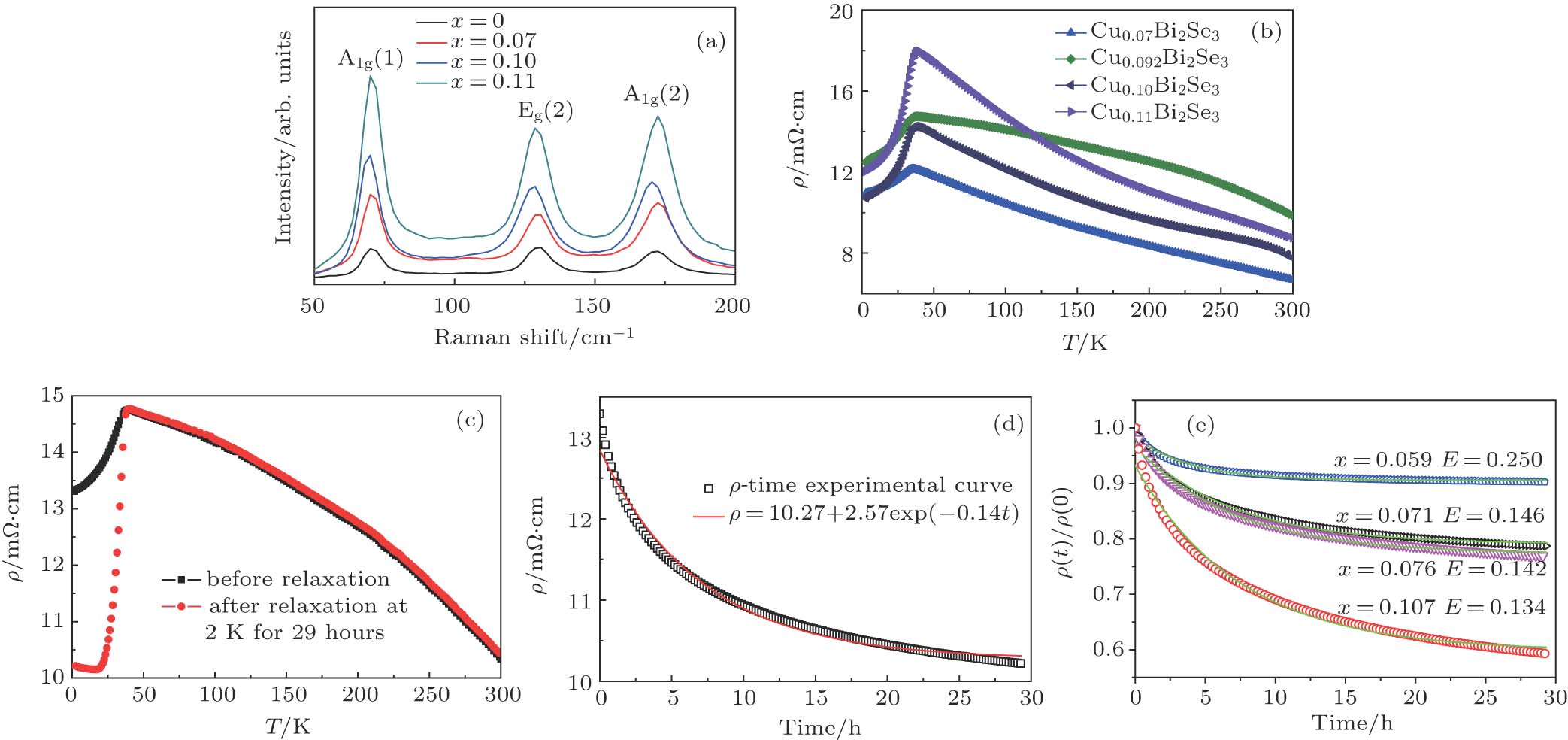Fig. 1. (color online) (a) Raman spectra of CuxBi2Se3 film samples with x = 0, 0.07, 0.10, and 0.11. (b) The resistivity of CuxBi2Se3 films with high Cu concentration dependence on temperature. (c) Temperature dependence of resistivity of Cu0.076Bi2Se3 (black square) and after (red circle) relaxation at 2 K for 29 h. (d) Time dependence of resistivity of Cu0.076Bi2Se3 at 2 K over the relaxation process of 29 h. (e) Time dependence of resistivity of CuxBi2Se3 with various Cu concentrations (x = 0.059, 0.071, 0.076, 0.107) at 2 K. Solid green lines are best fits. Modified from Li et al., Ref. [47]

Cu-intercalated CuxBi2Se3 shows superconductivity, making it a promising candidate for bulk topological superconductors.[46,48,49] Odd-parity nematic superconductivity is found in CuxBi2Se3 from bulk thermodynamic evidence, in which the nematicity emerges in the superconducting gap amplitude.[49] The superconductivity of Cu-doped Bi2Se3 is induced by dopant atoms intercalated in van der Waals gaps.[50] However, Sr atoms doped at interstitial locations are most likely to be responsible for the emergence of superconductivity in Sr-doped Bi2Se3, instead of those intercalated in van der Waals gaps. Remarkably stable re-emergent superconductivity is observed in SrxBi2Se3 at high pressure, concurrent with a structural phase transition.[51,52] A nodal superconducting gap is observed in Nb0.25Bi2Se3, consistent with odd-parity Cooper pairing.[53,54] The superconducting transition temperature TC continuously increases with pressure, which may be attributable to an electronic structure composed of multiple bands.[55] A Nb-doped Bi2Se3 superconductor with a trigonal crystal structure has been discovered, providing direct evidence that the superconducting magnetic response couples strongly to the underlying trigonal crystal symmetry.[56]

2.3. Transport properties of TIs modulated by others parameters

TI films are promising materials for optoelectronics because of their strong optical absorption and the thickness-dependent band gap of the topological surface states. Novel polarization-dependent photocurrent in photodetectors based on TI Bi2Te3 films under irradiation of linearly polarized light has been observed in experiments.[57] A significantly improved optoelectronic performance resulting from strain has been demonstrated using first-principles Hamiltonian calculation. The optical absorption of Bi2Se3 films with variable thickness is theoretically predicted to be effectively tuned by the application of uniaxial strain.[58] The intriguing electrical transport properties of compressed Sb2Te3 has been reported. A significant anomaly in the Hall coefficient at 3.4 GPa reveals an electronic topological transition. In addition, a semiconductor to semi-metal transition is observed at approximately 9.0 GPa because of the pressure-driven overlapping band.[59]

The linear magneto-resistance (MR) effect is an interesting topic because of its potential applications. The linear MR of single-crystalline TIs in a perpendicular field is attributed to the 2D gapless topological surface states and is of quantum origin; alternatively, it may be due to the charge inhomogeneity and conductivity fluctuation.[60,61] Granular films of Bi2Te3 nanoplates provide definite evidence for a sample’s physical or structural inhomogeneity as the origin of linear MR.[62] In Bi2Te3 films formed with Bi2Te3 nanoplates, a typical morphology is shown in Figs. 2(a)–2(c). As a semi-quantitative way to characterize the granularity of the film, six samples were selected. Figure 2(d) shows the number of nanoplates counted over an area of versus the average mobility. The results indicate that the higher density of nanoplates in the film leads to higher mobility because of the improved connectivity of the network. Three typical Bi2Te3 nanoplate film samples with linear MR effects are shown in Figs. 2(e)–2(g). The magnitude of the MR decreases with increasing temperature. Putting all the [R(B)−R(0)]/R(0), granularity, and temperature data for the six samples together in the same graph, a close correlation between the linear MR, average mobility, and the sample’s uniformity is revealed over a broad range of parameter space, as shown in Fig. 2(h). These results show that the linear MR can be attributed to large spatial fluctuations in the conductivity of the material, which is clear evidence for the phenomenological model of Parish–Littlewood. The observed linear MR in Bi2Se3 thin films is dominated by the inverse disorder parameter, which may be due to the very small carrier mobility. It is possible to tune Dirac surface states by applying external strain to single-crystalline Bi2Se3 nanowires. Surface states can be enhanced or destroyed by strain in the vicinity of grain boundaries on the surface of epitaxial Bi2Se3 thin films.[63–65]

Fig. 2. (color online) (a)–(c) SEM image of Bi2Te3 film samples formed with various Bi2Te3 nanoplates. (d) Number of nanoplate grains per area versus the average mobility of the film. (e)–(g) Magneto-resistance [R(B)−R(0)]/R(0) as a function of magnetic field at various temperatures for three different samples. (h) The relationship between mobility and [R(14T)−R(0)]/R(B = 0) for various samples with different granularities. Modified from Wang et al., Ref. [64].
3. Transport properties of TIs modulated by heterostructuring
3.1. TI/magnetic insulator (MI) heterostructures

The interface between a TI and an MI exhibits an interesting interplay of topological Dirac electrons and magnetism. The MI can be ferromagnetic or antiferromagnetic. The magnetic proximity effect between the TI and MI is considered to have great potential in spintronics. A promising example is the realization of the quantum anomalous Hall effect. Domain-wall Majorana bound states are predicted at the TI/MI interface.

As has been shown recently, based on ab initio calculations, Cr-doped (Bi,Sb)2Te3/GdI2 heterostructures are predicted to be QAH insulators with a nontrivial band gap. The breaking of time-reversal invariance by the magnetic order generates a nonzero Chern number that in turn leads to a Berry phase and a magnetoelectric effect. Moreover, it is predicted that a 3D QAH insulator could be realized in a (Bi2/3Cr1/3)2Te3/GdI2 superlattice. The magnetoelectric effect of the fluctuating electric field becomes nonlocal when the system is in the presence of a long-range Coulomb interaction between the Dirac electrons.[66,67] The transport properties of heterostructures formed by various types of MI/TI have been investigated.[68,69] High-quality antiferromagnetic MnSe films have been grown on a Bi2Se3 surface layer-by-layer, which reveals that an energy gap appears at the Dirac point of the original Bi2Se3 surface, possibly by breaking the time-reversal symmetry on the Bi2Se3 surface because of the magnetic proximity effect from MnSe.[68] A strong suppression of the weak antilocalization effect is observed in antiferromagnetic NiO/Bi2Se3 and attributed to the strong magnetic exchange field from the Ni electrons.[69] Giant spin-orbit torque-driven magnetization switching in NiFe/Bi2Se3 heterostructures has been directly shown at room temperature using a magneto-optic Kerr effect microscope.[70] Magnetic manipulation of the surface states on a single facet of a rectangular TI nanowire has been realized in Bi2Te3 nanowire/Fe3O4 substrates, breaking the local time-reversal symmetry and enhancing the gapping of the one-dimensional spectrum with a coupled ferromagnetic insulator substrate.[71] The transport properties of heterostructures formed by multilayers have also been studied theoretically, such as magnetic 3D TI thin films sandwiched between slabs of normal insulator, and two ferromagnetic insulators separated by a TI thin film, indicating that the spin-polarization magnitude is strongly dependent on the magnetic insertion position in the film and the particular electronic states of the TI contributing to the proximity effect can be directly identified through the coupling between two ferromagnetic insulators.[72,73] Proximity effect-induced superconductivity has been observed in epitaxial TI Bi2Se3 thin films grown on superconducting NbSe2 single crystals.[74] The superconducting transition temperature can be increased by pressure-induced enhanced coupling of the Fe1+yTe interfacial layer with the Bi2Te3 surface state.[75] Additionally, the chiral Majorana fermion mode is suggested in the hybrid system of a QAH TI thin film coupled with a superconductor.[76]

Emergent interfacial magnetic phenomena can be realized through artificial structural engineering by constructing heterostructures in MI/FM-IT, such as antiferromagnetic CrSb/ferromagnetic Cr-doped (Bi,Sb)2Te3,[77] in which proximity effects are shown to induce an interfacial spin texture modulation and establish an effective long-range exchange coupling. Dramatic enhancement of proximity exchange coupling has been reported in an MI/magnetic-TI EuS/Sb2−xVxTe3 hybrid heterostructure,[78] while the Dirac electron-mediated magnetic proximity effect is observed in TI (Bi0.2Sb0.8)2Te3/MI EuS heterostructures, which can be maximized by applying an electrical back gate.[79] Ferromagnetic resonance-driven spin pumping signals are observed at room temperature in 3D TI thin films-Y3Fe5O12 heterostructures, where the thin TI films can be Bi2Se3 or (Bi, Sb)2Te3. The results show that the spin-charge conversion efficiency increases dramatically as the TI film thickness increases.[80] The spin current induced by the coupling between the spin-momentum-locked surface states and magnons has been derived theoretically and observed in (Bi0.22Sb0.78)2Te3/permalloy (Py).[81,82] Unidirectional spin Hall resistance is observed in TI/FM heterostructures, including (Bi,Sb)2Te3/CoFeB and Bi2Se3/CoFeB bilayers. The original Dirac cone is destroyed and an interface state formed near the Fermi level as a result of the strong hybridization with the FM states.[83,84] The proximity effect is described by the exchange interaction between the delocalized electrons of the surface and bulk states in the Bi2Se3 film and localized Fe electrons in the Y3Fe5O12 film.[85] The temperature coefficients of the resistance of a (BixSb1−x)2Te3/SrRuO3 bilayer are suppressed, indicating the presence of a magnetic proximity effect in the bilayer.[86] Electron transport at the interface between TI and MI with magnetic skyrmions on the top has been investigated theoretically, finding that the skyrmions yield an additional contribution to the anomalous Hall conductivity.[87] Skyrmionium has also been observed in thin ferromagnetic films of Ni80Fe20/Cr-doped Sb2Te3. The occurrence of skyrmionium is tied to the ferromagnetic state of the topological insulator.[88] It has been shown that charge current flowing in-plane in a thin film of the topological insulator Bi2Se3 at room temperature can generate a strong spin-transfer torque on an adjacent ferromagnetic permalloy (Ni81Fe19) thin film, and this effect can be attributed to the topological surface states.[89]

3.2. TI/nonmagnetic materials heterostructures

Recent theories have predicted that the hybridization between graphene and TIs can create nontrivial spin textures in graphene, even leading to quantum spin Hall states.[90,91] A chiral magnetic structure is formed by graphene nanoribbons deposited on Sb2Te3 because of the interplay between strong spin-orbit coupling and broken inversion symmetry.[92] The anisotropic spin transport in graphene–Bi2Se3 has been revealed by theoretical predictions to be caused by the spin proximity effect, with a dependence of the anisotropy on the geometry of the interface.[93] figure 3 shows the spin lifetime anisotropy in graphene–Bi2Se3 heterostructures with panels (a) and (b) for small and large unit cells, respectively. In the small unit cell, the anisotropy remains negligible far from the graphene Dirac point and reaches values in the hundreds near the Dirac point. Figure 3(b) shows the anisotropy in the large unit cell. Both the tight-binding (TB) fit and the analytical prediction show good agreement with the density functional theory (DFT) results. In this case, the anisotropy is characterized by a strong electron-hole asymmetry.[94] A giant negative anomalous magneto-transport property for graphene–Bi2Se3 heterojunctions has been reported, which is enhanced by applying a perpendicular negative magnetic field because of the electronic coupling between graphene and the topological surface state.[94] The spin-polarized current from a TI can be injected into graphene in a van der Waals epitaxial Bi2Te2Se–graphene heterostructure, which indicates that spin manipulation can be achieved by purely electrical means.[95]

Fig. 3. (color online) Spin lifetime anisotropy of graphene/Bi2Se3 heterostructures as a function of energy relative to the graphene Dirac point. Panels (a) and (b) show the anisotropy in small and large unit cells, respectively. Modified from Song et al., Ref. [95].

Vertically stacked p–n junctions can be formed by combining n-type Bi2Te3 and p-type Sb2Te3 TIs. The surface and bulk transport modes of vertical Bi2Te3/Sb2Te3 heterostructures are disentangled by measuring magneto-transport with varying relative thicknesses.[96] The thermoelectric conversion capability of lateral heterostructures has been experimentally investigated, consisting of n-type Bi2Te2Se and p-type Sb2Te3, which showed a high thermoelectric performance at room temperature.[97] P-type Sb2Te3/n-type strontium titanate heterostructures exhibit pronounced photovoltaic behavior over a wide range of temperatures because of a strong built-in field at the heterointerface.[98] N-Bi2Se3 nanoflake/p-Si nanowire heterojunction devices have been fabricated, showing high performance in the near-infrared region.[99] N-type TI Bi2Te3/p-Si junctions demonstrate nonlinear diode-type characteristics. The schematic for measuring the n-Bi2Te3/p-Si junctions’ photo-properties is shown in Fig. 4. The photovoltaic effect at various wavelengths for a typical sample is shown in Fig. 5(a). Clear p–n diode properties are found in smooth Bi2Te3 films formed with large Bi2Te3 nanoplates, which show a good photovoltaic effect with broadband photo-response across the UV, visible, and NIR wavelength range.[100] The photovoltage can be effectively switched on and off while the light source is turned on and off under light illumination with various wavelengths of light, as shown in Fig. 5(b). The Kohn anomalies are observed at the surface of Bi2Te3/GaAs, demonstrating important electron–phonon coupling effects.[101] Anomalous photogalvanic effects in (Bi0.5Sb0.5)2Te3/GaAs have been reported, and the helicity-dependent photocurrent can be modulated by the gate voltage.[102]

Fig. 4. (color online) Schematic for measuring the photo-properties structure of n-Bi2Te3/p-Si junctions. Modified from Wang et al., Ref. [102].
Fig. 5. (color online) (a) The characteristics of n-Bi2Te3/p-Si junctions in the dark and under illumination with various wavelengths of light. (b) The dependence of junction photovoltage on time under light illumination with various wavelengths of light. Modified from Wang et al., Ref. [102].
4. Summary and outlook

In this review paper, we have discussed some of the most exciting and promising research on the characterization and transport properties of TIs modified by doping or heterostructuring. Doping TIs with magnetic elements introduces large magnetic moments and results in high crystal quality with high doping concentrations. The paramagnetic state, ferromagnetic state, and antiferromagnetic state have been observed in TIs doped with rare earth ions, transition metals, and so on. The QAH is proposed in ferromagnetic TIs. The ferromagnetic state with the highest TC ∼250 K was reported in Cr-doped Sb2Te3 films. An insulator-metal transition below ∼37 K was observed in CuxBi2Se3 films because of electron delocalization resulting from the strong hybridization between Cu+ and Cu2+ conduction bands. The superconductivity of Cu- and Sr-doped Bi2Se3 was induced by dopant atoms intercalated in van der Waals gaps or interstitial locations. Heterostructures of TIs with other materials have been studied because their interface exhibits interesting interplay effects. The magnetic proximity effect between a TI and MI can induce many interesting properties, such as the chiral Majorana fermion mode, which was suggested in an AQH TI thin film coupled with a superconductor; the spin current induced by coupling between the spin-momentum-locked surface state and magnons; and skyrmions, which make an additional contribution to the anomalous Hall conductivity at the interface between TI and MI with magnetic skyrmions. Topological crystalline insulators (TCIs), as a new member of the TI family, have received attention recently because their surface carries an even number of Dirac cones protected by crystalline symmetry, which is different from the well-known TIs. An even number of Dirac surface states for TCIs leads to many fascinating topological phenomena in theory.[103,104] The intermediate valent Kondo insulator SmB6 is proposed to be a TI, and the low-temperature conductivity of SmB6 can be explained by a topologically protected metallic surface state, as expected in TI.[105,106] Many fascinating topological phenomena are waiting to be discovered and investigated with experiments. Many of these novel effects have been investigated theoretically, while experimental studies are more challenging. Therefore, it is necessary to achieve more progress in this area experimentally.

Reference
[1] Zhang H J Liu C X Qi X L Dai X Fang Z Zhang S C 2009 Nat. Phys. 5 438
[2] Chen Y L Analytis J G Chu J H Liu Z K Mo S K Qi X L Zhang H J Lu D H Dai X Fang Z Zhang S C Fisher I R Hussain Z Shen Z X 2009 Science 325 178
[3] Cha J J Kong D S Hong S S Analytis J G Lai K Cui Y 2012 Nano Lett. 12 1107
[4] Chen J He X Y Wu K H Ji Z Q Lu L Shi J R Smet J H Li Y Q 2011 Phys. Rev. 83 241304 R
[5] Cao H L Venkatasubramanian R Liu C Pierce J Yang H Hasan M Z Wu Y Chen Y P 2012 Appl. Phys. Lett. 101 162104
[6] Chen J Qin H J Yang F Liu J Guan T Qu F M Zhang G H Shi J R Xie X C Yang C L Wu K H Li Y Q Lu L 2010 Phys. Rev. Lett. 105 176602
[7] Kim Y S Brahlek M Bansa N Edrey E Kapilevich G A Iida K Tanimura M Horibe Y Cheong S W Oh S 2011 Phys. Rev. 84 073109
[8] Steinberg H Laloë J B Fatemi V Moodera J S Jarillo-Herrero P 2011 Phys. Rev. 84 233101
[9] Wang Z H Gao X P A Zhang Z D 2017 Outlook Challenges Nano Devices Sensors MEMS Springer Ting Li & Ziv Liu 429
[10] Liu Y Ma Z Zhao Y F Meenakshi S Wang J 2013 Chin. Phys. 22 067302
[11] Yu R Zhang W Zhang H J Zhang S C Dai X Fang Z 2010 Science 329 61
[12] Lee C H He R Wang Z H Qiu R L J Kumar A Delaney C Beck B Kidd T E Chancey C C Sankaran R M Gao X P A 2013 Nanoscale 5 4337
[13] Zhang S Li Z G Pan X C Wang X F Song F Q 2015 Solid State Commun. 223 45
[14] Zhang M Liu L G Yang H 2016 J. Alloys Compd. 678 463
[15] Martínez-Velarte M C Kretz B Moro-Lagares M Aguirre M H Riedemann T M Lograsso T A Morellón L Ibarra M R Garcia-Lekue Arán Serrate D 2017 Nano Lett. 17 4047
[16] Niu W Du K Wang S B Zhang M H Gao M Chen Y D Liu H Zhou W Song F Q Wang P Xu Y B Wang X F Shen J Zhang R 2017 Nano Scale 9 12372
[17] Stolyarov V S Remizov S V Shapiro D S Pons S Vlaic S Aubin H Baranov D S Brun C Yashina L V Bozhko S I Cren T Pogosov W V Roditchev D 2017 Appl. Phys. Lett. 111 251601
[18] Gupta S Kanai S Matsukura F Ohno H 2017 Appl. Phys. Exp. 10 103001
[19] Zhang L G Zhao D P Zang Y Y Yuan Y H Jiang G Y Liao M H Zhang D He K Ma X C Xue Q K 2017 APL Mater. 5 076106
[20] Kim J Jhi S H MacDonald A H Wu R 2017 Phys. Rev. 96 140410 R
[21] Ou Y B Liu C Jiang G Y Feng Y Zhao D Y Wu W X Wang X X Li W Song C L Wang L L Wang W B Wu W D Wang Y Y He K Ma X C Xue Q K 2018 Adv. Mater. 30 1703062
[22] Zhang J Chang C Z Tang P Z Zhang Z C Feng X Li K Wang L L Chen X Liu C X Duan W H He K Xue Q K Ma X C Wang Y Y 2013 Science 339 1582
[23] Tiwari K L Coish W A Pereg-Barnea T 2017 Phys. Rev. 96 235120
[24] Feng X Feng Y Wang J Ou Y B Hao Z Q Liu C Zhang Z C Zhang L G Lin C J Liao J Li Y Q Wang L L Ji S H Chen X Ma X C Zhang S C Wang Y Y He K Xue Q K 2016 Adv. Mater. 28 6386
[25] Chang C Z Zhang J Feng X Shen J Zhang Z C Guo M H Li K Ou Y B Wei P Wang L L Ji Z Q Feng Y Ji S Chen X Jia J F Dai X Fang Z Zhang S C He K Wang Y Y Lu L Ma X C Xue Q K 2013 Science 340 167
[26] West D Sun Y Y Wang H Bang J Zhang S B 2012 Phys. Rev. 86 121201 R
[27] Lüpke F Eschbach M Heider T Lanius M Schüffelgen P Rosenbach D von den Driesch N Cherepanov V Mussler G Plucinski L Grützmacher D Schneider C M Voigtländer B 2017 Nat. Commun. 8 15704
[28] Yoshimi R Tsukazaki A Kozuka Y Falson J Takahashi K S Checkelskýw J G Nagaosa N Kawasaki M Tokura Y 2015 Nat. Commun. 6 6627
[29] Taskin A A Legg H F Yang F Sasaki S Kanai Y Matsumoto K Rosch A Ando Y 2017 Nat. Commun. 8 1340
[30] Satake Y Shiogai J Takane D Yamada K Fujiwara K Souma S Sato T Takahashi T Tsukazaki A 2018 J. Phys.: Condens Matter 30 085501
[31] Wang Z H Qiu R L J Lee C H Zhang Z D Gao X P A 2013 ACS Nano 7 2126
[32] Li C de Ronde B Nikitin A Huang Y Golden M S de Visser A Brinkman A 2017 Phys. Rev. 96 195427
[33] Knispel T Jolie W Borgwardt N Lux J Wang Z Ando Y Rosch A Michely T Grüninger M 2017 Phys. Rev. 96 195135
[34] Pan Y Wang Q Z Yeats A L Pillsbury T Flanagan T C Richardella A Zhang H Awschalom D D Liu C X Samarth N 2017 Nat. Commun. 8 1037
[35] Urkude R R Rawat R Palikundwar U A 2017 J. Phys.: Condens. Matter 29 495602
[36] Dubroka A Caha O Hronček M Friš P Orlita M Holý V Steiner H Bauer G Springholz G Humlíček J 2017 Phys. Rev. 96 235202
[37] Singh S Gopal R K Sarkar J Pandey A Patel B G Mitra C 2017 J. Phys.: Condens. Matter 29 505601
[38] Checkelsky J G Hor Y S Cava R J Ong N P 2011 Phys. Rev. Lett. 106 196801
[39] Autore M Giorgianni F D’ Apuzzo F Gaspare A D Vecchio I L Brahlek M Koirala N Oh S Schade U Ortolanic M Lupi S 2016 Nanoscale 8 4667
[40] Zhang M Li Y Song F Wang X Zhang R 2017 Chin. Phys. 26 127305
[41] Zhang M Wang H Mu K Wang P Niu W Zhang S Xiao G Chen Y Tong T Fu D Wang X Zhang H Song F Miao F Sun Z Xia Z Wang X Xu Y Wang B Xing D Zhang R 2018 ACS Nano 12 1537
[42] Tanaka Y Nakayama K Souma S Sato T Xu N Zhang P Richard P Ding H Suzuki Y Das P Kadowaki K Takahashi1 T 2012 Phys. Rev. 85 125111
[43] Chen T S Chen Q Schouteden K Huang W K Wang X F Li Z Miao F Wang X R Li Z G Zhao B Li S C Song F Q Wang J L Wang B G Haesendonck C V Wang G H 2014 Nat. Commun. 5 5022
[44] Brahlek M Koirala N Salehi M Bansal N Oh S 2014 Phys. Rev. Lett. 113 26801
[45] Li M Z Wang Z H Yang L Gao X P A Zhang Z D 2017 J. Phys. Chem. Solids 1 x
[46] Hor Y S Williams A J Checkelsky J G Roushan P Seo J Xu Q Zandbergen H W Yazdani A Ong N P Cava R J 2010 Phys. Rev. Lett. 104 057001
[47] Li M Z Wang Z H Yang L Li D Yao Q R Rao G H Gao Xuan P A Zhang Z D 2017 Phys. Rev. 96 075152
[48] Kriener M Segawa K Ren Z Sasaki S Ando Y 2011 Phys. Rev. Lett. 106 127004
[49] Yonezawa S Tajiri K Nakata S Nagai Y Wang Z Segawa K Ando Y Maeno Y 2017 Nat. Phys. 13 123
[50] Shirasawa T Sugiki M Hirahara T Aitani M Shirai T Hasegawa S Takahashi T 2014 Phys. Rev. 89 195311
[51] Li Z Wang M Zhang D Feng N Jiang W Han C Chen W Ye M Gao C Jia J Li J Qiao S Qian D Xu B Tian H Gao B 2018 Phys. Rev. Mater. 2 014201
[52] Zhou Y Chen X Zhang R Shao J Wang X An C Zhou Y Park C Tong W Pi L Yang Z Zhang C Zhang Y 2016 Phys. Rev. 93 144514
[53] Smylie M P Claus H Welp U Kwok W K Qiu Y Hor Y S Snezhko A 2016 Phys. Rev. 94 180510
[54] Smylie M P Willa K Claus H Snezhko A Martin I Kwok W K Qiu Y Hor Y S Bokari E Niraula P Kayani A Mishra V Welp U 2017 Phys. Rev. 96 115145
[55] Smylie M P Willa K Ryan K Claus H Kwok W K Qiu Y Hor Y S Welp U 2017 Physica 543 58
[56] Asaba T Lawson B J Tinsman C Chen L Corbae P Li G Qiu Y Hor Y S Fu L Li L 2017 Phys. Rev. X 7 011009
[57] Yao J D Shao J M Li S W Bao D H Yang G W 2015 Sci. Rep. 5 14184
[58] Brems M R Paaske J Lunde A M Willatzen M 2018 Phys. Rev. 97 081402 R
[59] Zhang J Hu T Yan J Ke F Wang J Cui X Li X Ma Y Yang J Gao C 2017 Mater. Lett. 209 78
[60] Tang H Liang D Qiu Richard L J Gao X P A 2011 ACS Nano 5 7510
[61] He H T Liu H C Li B K Guo X Xu Z J Xie M H Wang J N 2013 Appl. Phys. Lett. 103 031606
[62] Wang Z H Yang L Li X J Zhao X T Wang H L Zhang Z D Gao X P A 2014 Nano Lett. 14 6510
[63] Wang W J Gao K H Li Q L Li Z Q 2017 Appl. Phys. Lett. 111 232105
[64] Schindler C Wieg C Sichau J Tiemann L Nielsch K Zierold R Blick R H 2017 Appl. Phys. Lett. 111 171601
[65] Liu Y Li Y Y Rajput S Gilks D Lari L Galindo P L Weinert M Lazarov V K Li L 2014 Nat. Phys. 10 294
[66] Xu G Wang J Felser C Qi X L Zhang S C 2015 Nano Lett. 15 2019
[67] Rex S Nogueira F S Sudbø A 2016 Phys. Rev. 93 014404
[68] Matetskiy A V Kibirev I A Hirahara T Hasegawa S Zotov A V Saranin A A 2015 Appl. Phys. Lett. 107 091604
[69] Bhowmick T Jerng S K Jeon J H Roy S B Kim Y H Seo J Kim J S Chun S H 2017 Nanoscale 9 844
[70] Wang Y Zhu D Wu Y Yang Y Yu J Ramaswamy R Mishra R Shi S Elyasi M Teo K L Wu Y Yang H 2017 Nat. Commun. 8 1364
[71] Gooth J Zierold R Sergelius P Hamdou B Garcia J Damm C Rellinghaus B Pettersson H J Pertsova A Canali C Borg M Nielsch K 2016 ACS Nano 10 7180
[72] Meńshov V N Tugushev V V Chulkov E V 2016 JETP Lett. 104 453
[73] Li M Cui W Yu J Dai Z Wang Z Katmis F Guo W Moodera J 2015 Phys. Rev. 91 014427
[74] Dai W Richardella A Du R Zhao W Liu X Liu C X Huang S H Sankar R Chou F Samarth N Li Q 2017 Sci. Rep. 7 7631
[75] Shen J Heuckeroth C Deng Y He Q Liu H C Liang J Wang J Sou I K Schilling J S Lortz R 2017 Physica 543 18
[76] He Q L Pan L Stern A L Burks E C Che X Yin G Wang J Lian B Zhou Q Choi E S Murata K Kou X Chen Z Nie T Shao Q Fan Y Zhang S C Liu K Xia J Wang K L 2017 Science 357 294
[77] He Q L Kou X Grutter A J Yin G Pan L Che X Liu Y Nie T Zhang B Disseler S M Kirby B J Ratcliff W Shao Q Murata K Zhu X Yu G Fan Y Montazeri M Han X Borchers J A Wang K L 2017 Nat. Mater. 16 94
[78] Li M Chang C Z Kirby B J Jamer M E Cui W Wu L Wei P Zhu Y Heiman D Li J Moodera J S 2015 Phys. Rev. Lett. 115 087201
[79] Li M Song Q Zhao W Garlow J A Liu T H Wu L Zhu Y Moodera J S Chan M H W Chen G Chang C Z 2017 Phys Rev 96 201301 R
[80] Wang H Kally J Lee J S Liu T Chang H Hickey D R 2016 Phys. Rev. Lett. 117 076601
[81] Okuma N Nomura K 2017 Phys. Rev. 95 115403
[82] Mendes J B S Santos O A Holanda J Loreto R P de Araujo C I L Chang C Z Moodera J S Azevedo A Rezende S M 2017 Phys. Rev. 96 180415 R
[83] Lv Y Kally J Zhang D Lee J S Jamali M Samarth N Wang J P 2018 Nat. Commun. 9 111
[84] Hsu Y T Park K Kim E A 2017 Phys. Rev. 96 235433
[85] Kubota Y Murata K Miyawaki J Ozawa K Onbasli M C Shirasawa T Feng B Yamamoto S Liu R Y Yamamoto S Mahatha S K Sheverdyaeva P Moras P Ross C A Suga S Harada Y Wang K L Matsuda I 2017 J. Phys.: Condens. Matter 29 055002
[86] Koren G 2018 Phys. Rev. 97 054405
[87] Araki Y Nomura K 2017 Phys. Rev. 96 165303
[88] Zhang S Kronast F van der Laan G Hesjedal T 2018 Nano Lett. 18 1057
[89] Mellnik A R Lee J S Richardella A Grab J L Mintun P J Fischer M H Vaezi A Manchon A Kim E A Samarth N Ralph D C 2014 Nature 511 449
[90] Kou L Hu F Yan B Wehling T Felser C Frauenheim T Chen C 2015 Carbon 87 418
[91] Jin K H Jhi S H 2013 Phys. Rev. 87 075442
[92] Zhang W Hajiheidari F Mazzarello R 2017 Phys. Rev. 96 245413
[93] Song K Soriano D Cummings A W Robles R Ordejón P Roche S 2018 Nano Lett. 18 2033
[94] Zhang L Lin B C Wu Y F Wu H C Huang T W Chang C R Ke X Kurttepeli M Tendeloo G V Xu J Yu D Liao Z M 2017 ACS Nano 11 6277
[95] Vaklinova K Hoyer A Burghard M Kern K 2016 Nano Lett. 16 2595
[96] Backes D Huang D Mansell R Lanius M Kampmeier J Ritchie D Mussler G Gumbs G Grützmacher D Narayan V 2017 Phys. Rev. 96 125125
[97] Mashhadi S Duong D L Burghard M Kern K 2017 Nano Lett. 17 214
[98] Sun H Jiang T Zang Y Zheng X Gong Y Yan Y Xu Z Liu Y Fang L Cheng X He K 2017 Nanoscale 9 9325
[99] Das B Das N S Sarkar S Chatterjee B K Chattopadhyay K K 2017 ACS Appl. Mater. Interfaces 9 22788
[100] Wang Z H Li M Z Yang L Zhang Z D Gao X P A 2017 Nano Res. 10 1872
[101] Wiesner M Trzaskowska A Mroz B Charpentier S Wang S Song Y Lombardi F Lucignano P Benedek G Campi D Bernasconi M Guinea F Tagliacozzo A 2017 Sci. Rep. 7 16449
[102] Qu D X Che X Kou X Pan L Crowhurst J Armstrong M R Dubois J Wang K L Chapline G F 2018 Phys. Rev. 97 045308
[103] Fu L 2011 Phys. Rev. Lett. 106 106802
[104] Liu J W Hsieh T H Wei P Duan W H Moodera J Fu L 2014 Nat. Mater. 13 178
[105] Sundermann M Yavaş H Chen K Kim D J Fisk Z Kasinathan D Haverkort M W Thalmeier P Severing A Tjeng L H 2018 Phys. Rev. Lett. 120 016402
[106] Nam M S Williams B H Chen Y Contera S Yao S Lu M Chen Y F Timco G A Muryn C A Winpenny R E P Ardavan A 2018 Nat. Commun. 9 56