† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 91434204).
Fundamental understanding of the wettability of curved substrates is crucial for the applications of microdroplets in colloidal science, microfluidics, and heat exchanger technologies. Here we report via lattice Boltzmann simulations and energetic analysis that microdroplets show an ability of transporting selectively to appropriate substrates solely according to substrate shape (curvature), which is called the substrate-curvature-dependent droplet targeting because of its similarity to protein targeting by which proteins are transported to the appropriate destinations in the cell. Two dynamic pathways of droplet targeting are identified: one is the Ostwald ripening-like liquid transport between separated droplets via evaporating droplets on more curved convex (or less curved concave) surfaces and growing droplets on less curved convex (or more curved concave) surfaces, and the other is the directional motion of a droplet through contacting simultaneously substrates of different curvatures. Then we demonstrate analytically that droplet targeting is a thermodynamically driven process. The driving force for directional motion of droplets is the surface-curvature-induced modulation of the work of adhesion, while the Ostwald ripening-like transport is ascribed to the substrate-curvature-induced change of droplet curvature radius. Our findings of droplet targeting are potentially useful for a tremendous range of applications, such as microfluidics, thermal control, and microfabrication.
The directional motion[1] of sessile droplets on solid surfaces has been an active topic for both experimental and theoretical investigations. In nature, surfaces that are capable of transporting liquid droplets are ubiquitous, such as butterfly wings,[2,3] rice leaves,[4,5] and feathers of ducks and geese.[6] Inspired by these surfaces, various methods have been developed to prepare surfaces with similar directional liquid transport ability,[7,8] which shows potential for a tremendous range of applications from anti-icing,[9,10] dip-pen nanolithography, to oil/water separation. On the one hand, solid surfaces with a specific curvature gradient are designed to collect the droplet through directional movement of droplets.[11–15] On the other hand, spontaneous motion of droplets has also been found on the heterogeneous substrates with wettability gradients.[16–21]
In this paper, we report via lattice Boltzmann simulations and energetic analysis that depending on their curvature, various substrates show different abilities for sorting droplets, i.e., droplets are capable of directional transportation targeting certain substrates with the appropriate shape (curvature). For the substrate-curvature-dependent droplet targeting, two dynamic pathways of droplet targeting are identified in this work: Ostwald ripening-like liquid transport between droplets without direct contact, and directional motion of droplets through contacting substrates of different curvatures simultaneously. Then we interpret the behaviors of droplet targeting as a result of free energy change due to the difference of substrate curvatures.
In the present work, the lattice Boltzmann (LB) method, a numerically robust technique[22,23] for simulating interfacial phenomena, was used to reveal the behaviors of the droplet targeting according to substrate curvature. We applied the three dimensional multicomponent and multiphase Shan–Chen (SC) type LB method[24,25] based on the D3Q19 lattice,[26] which has particularly been successfully used to study droplets wetting on spherical substrates.[27] In this model, a pseudopotential was employed to represent different interactions with the potential function of 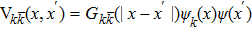
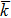
In this work, simulation boxes range from 100 × 100 × 70 to 100 × 100 × 130, in which one or two droplets interact selectively with substrates of different curvatures. All the quantities are reported here in dimensionless LB units. To simplify the description, we sometimes called the convex spherical substrates as colloids. Our extensive LB simulations reveal that microdroplets have the ability to select the substrates having an appropriate shape according to substrate curvature. The droplet selectivity of substrates is called droplet targeting or droplet sorting here, because of its similarity to protein targeting, by which proteins are transported to the appropriate destinations in the cell.
Our simulations show that there exist at least two different pathways for droplet targeting. The first one resembles Ostwald ripening that refers to, e.g., in an emulsion system, the growth of large emulsions from those of smaller size because the larger emulsions are more energetically favorable than smaller ones. Different from emulsion coalescence for which neighboring emulsions come into direct contact and coalesce, Ostwald ripening occurs with the external environment (solvent) serving as the transfer medium. In our study, we also found similar behavior for sessile droplets without direct contact.
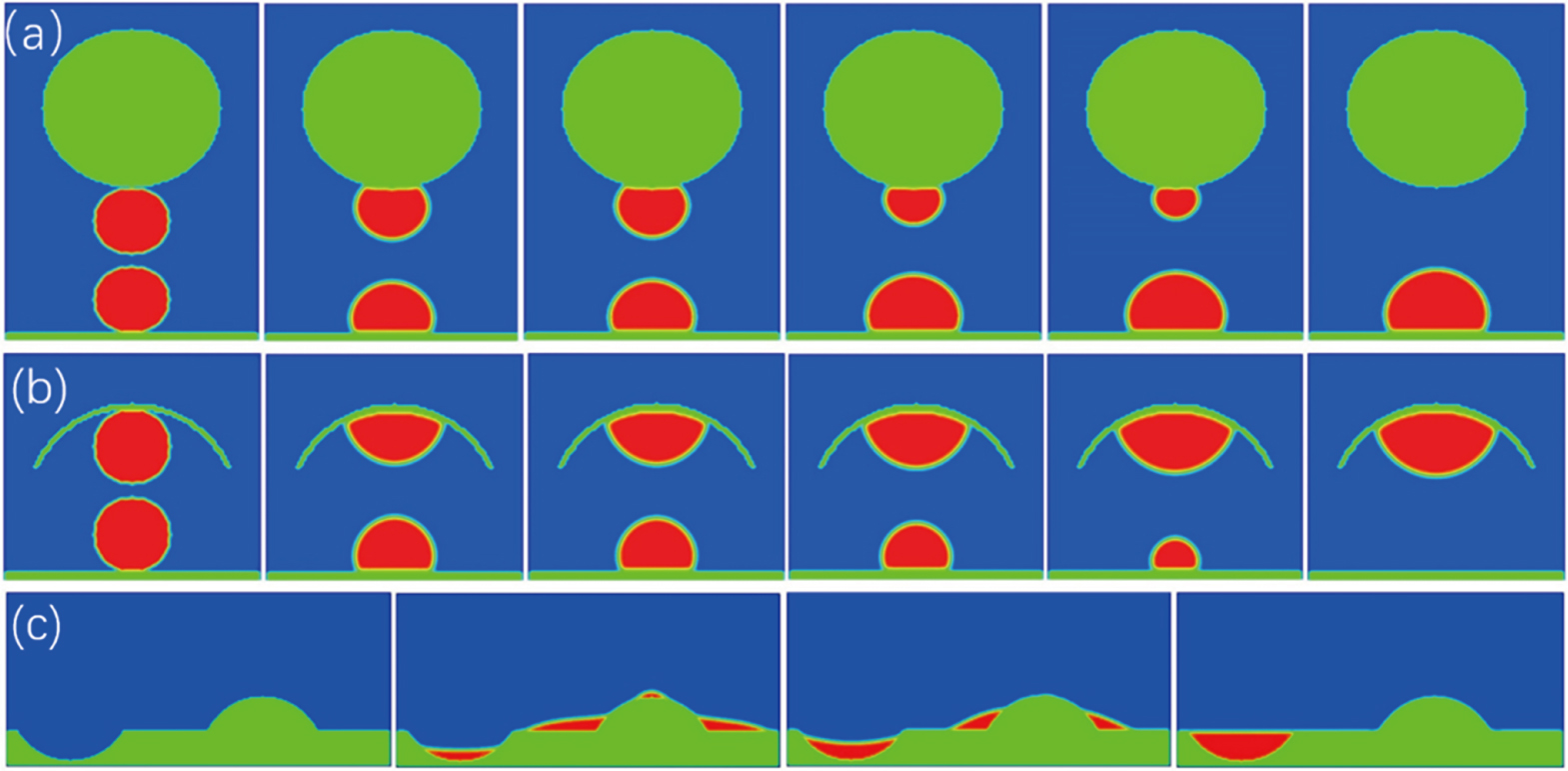
At the beginning of our simulations, for example, we placed two droplets of the same initial radius of rS = 15 close to respectively the spherical colloid of a curvature radius R = 30 and a flat substrate (Fig.
The Ostwald ripening-like droplet targeting also occurs between two droplets placed respectively on a flat substrate and a concave spherical substrate (see Fig.
As a particular example, we simulated a vapor condensation process near a rough substrate having regions of different (convex, flat, and concave) local curvatures (see Fig.
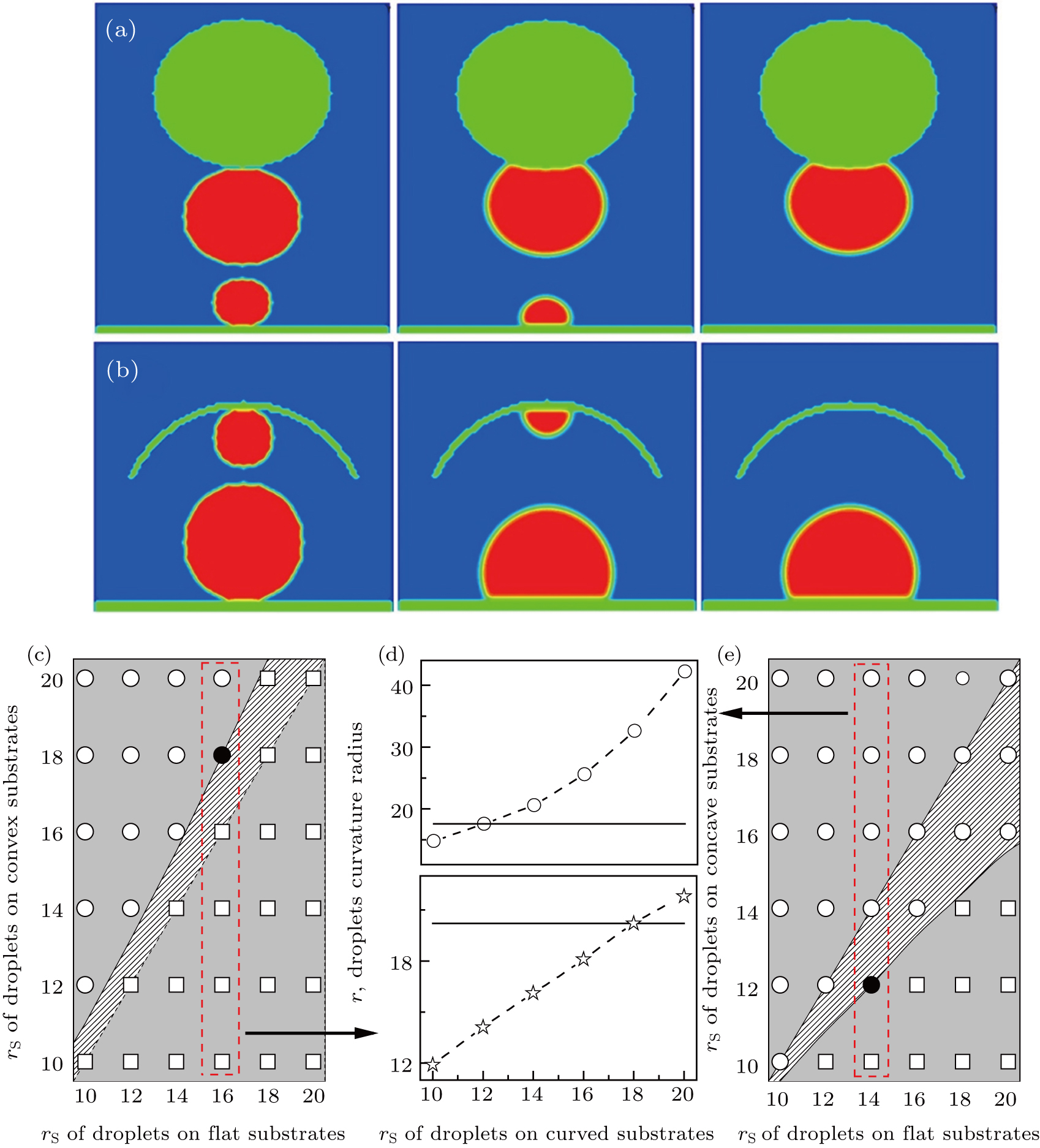
To reveal the mechanism of microdroplets targeting via a pathway of Ostwald ripening, we performed extensive simulations for different sized droplets on, respectively, a curved and a flat substrate (see, e.g., Figs.
We also investigated the dynamic characteristics of the processes, and the time evolution of free energy, contact angle, and curvature radius is shown in Figs. s1–s4 in the supporting information. As expected, during the processes of spontaneous transport, the free energy decreases with time, and the contact angle remains constant and is nearly equal to Young’s contact angle θY.
We also identified another pathway for droplet targeting the specific substrate according to substrate curvature: directional motion of a droplet that contacts simultaneously different substrates. For example, we initially placed a droplet with a radius rS = 15 in between two spherical colloids having a radius of 10 and 30 (Fig.
Similarly, when a droplet was initially placed into the confined space between a flat substrate and a spherical colloid with a curvature radius of R = 30, it would slowly leave the colloid and move to wet the flat substrate having an infinite large curvature radius (Fig.
To interpret how the substrate geometry affects droplet targeting, we considered firstly whether Young’s equation is affected by the curvature of spherical substrates. In fact, Wu et al.[31] have proved theoretically that Young’s equation works for droplets on the convex and concave spherical surfaces, i.e., the contact angle of a sessile droplet on spherical surfaces satisfies 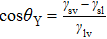
To distinguish the driving force for the Ostwald ripening-like transport and the surface-curvature-induced droplet movement observed in our simulations, we need to determine theoretically the geometric features of different sessile droplets on substrates with various curvatures as well as the corresponding free energy. As usual, we assumed that the sessile droplets considered have a constant volume and their vapor–liquid interfaces are of spherical shape. The volume V for a droplet having an apparent contact angle θ and a curvature radius r is given by
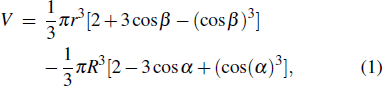 |
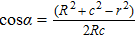
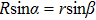
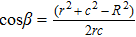

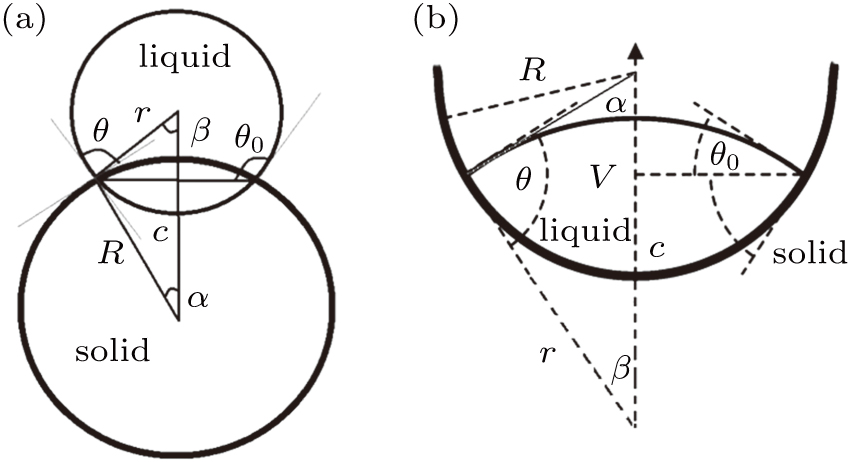 | Fig. 4. Schematic illustration of the wetting of a liquid droplet on (a) the outer surface of a spherical colloid and (b) the inner surface of a spherical cavity. |
For a droplet placed on a spherical surface, the total free energy G reads
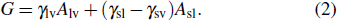 |
For a droplet with a given volume V, we can determine the unknown variables α and r according to Eq. (
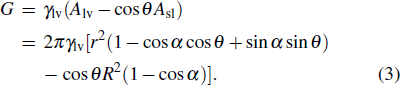 |
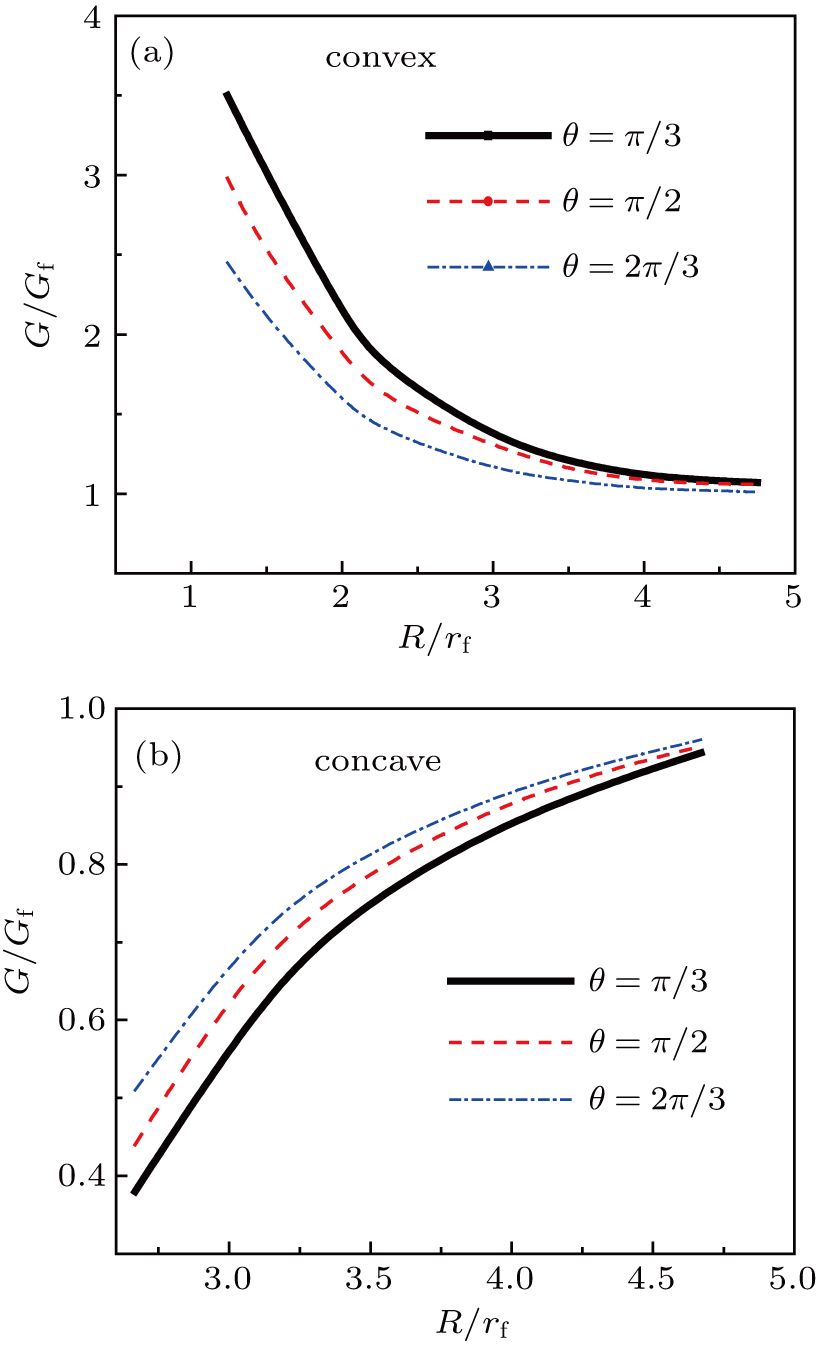
To interpret the substrate-curvature-induced droplet targeting, we calculated the free energy of a droplet on various colloids of different curvatures. As a comparison, the free energy for a droplet sitting on a flat surface can be obtained[15] from 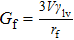
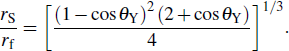 |
Figure
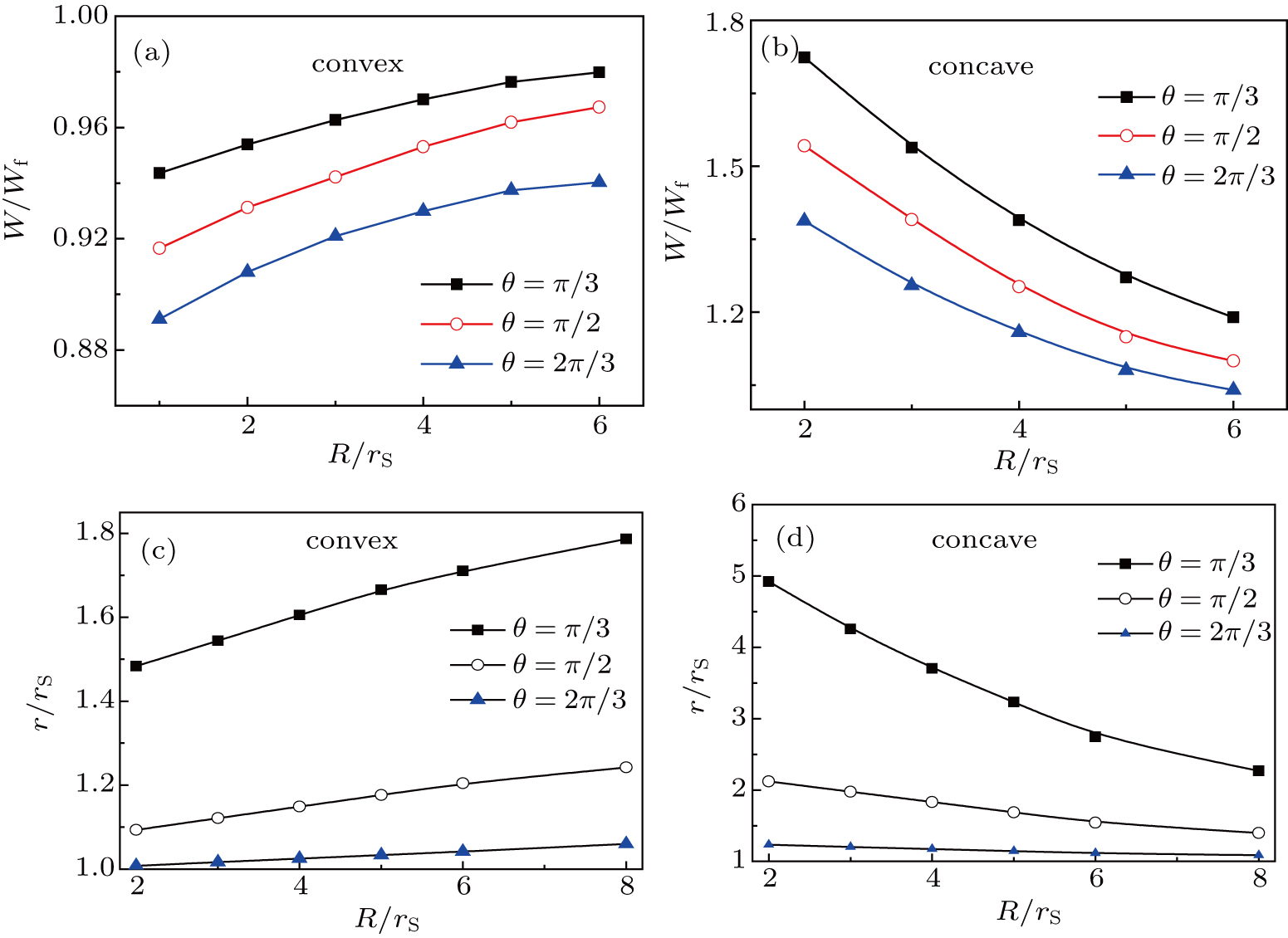
Above we show that the droplet targeting is a thermodynamically-driven process. More specifically, here we ascribed the difference of the work of adhesion to the driving force for the surface-curvature-induced directional droplet motion (Fig.
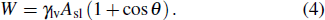 |
For the driving force of the Ostwald ripening-like transport, we ascribed the increase of stability of the sessile droplets to the increase of droplet curvature radius on less curved convex (or more curved concave) substrates (Figs.
The Ostwald ripening-like transport found here, including the reverse Ostwald ripening, originates from different curvature radii among droplets, or equivalently, the different pressures of vapor around the droplets of different curvatures since the Laplace pressure ΔP ∼ 1/r, which means that the pressure of the surrounding vapor in equilibrium with a droplet of larger curvature radius is lower than that for a droplet of smaller curvature radius. Therefore, the liquid is always transferred to the droplets with a larger curvature radius, but not necessarily the ones with a larger volume, because the droplets of the same volume on substrates of different curvatures could exhibit different curvature radii. This is why the reverse Oswald ripening occurs. For droplets sitting respectively on substrates of different curvatures, in some cases the curvature radii of larger droplets may become relatively smaller than those for the smaller droplets, which leads to the reverse Ostwald ripening-like transport.
We report via lattice Boltzmann simulations that droplets show an ability of selectively targeting the substrate with appropriate curvature. Simulation results show that there exist at least two pathways for the behavior of droplet targeting: Ostwald ripening-like liquid transport between separated droplets and directional motion of droplets via simultaneously contacting substrates of different curvatures. Then we demonstrate through theoretical analysis that droplet targeting is a thermodynamically-driven process. The directional motion of droplets is ascribed to the difference of the work of adhesion for the droplet contacting with substrates of different curvature, while the Ostwald ripening-like transport is ascribed to the change of droplet curvature radius depending on substrate curvature.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |