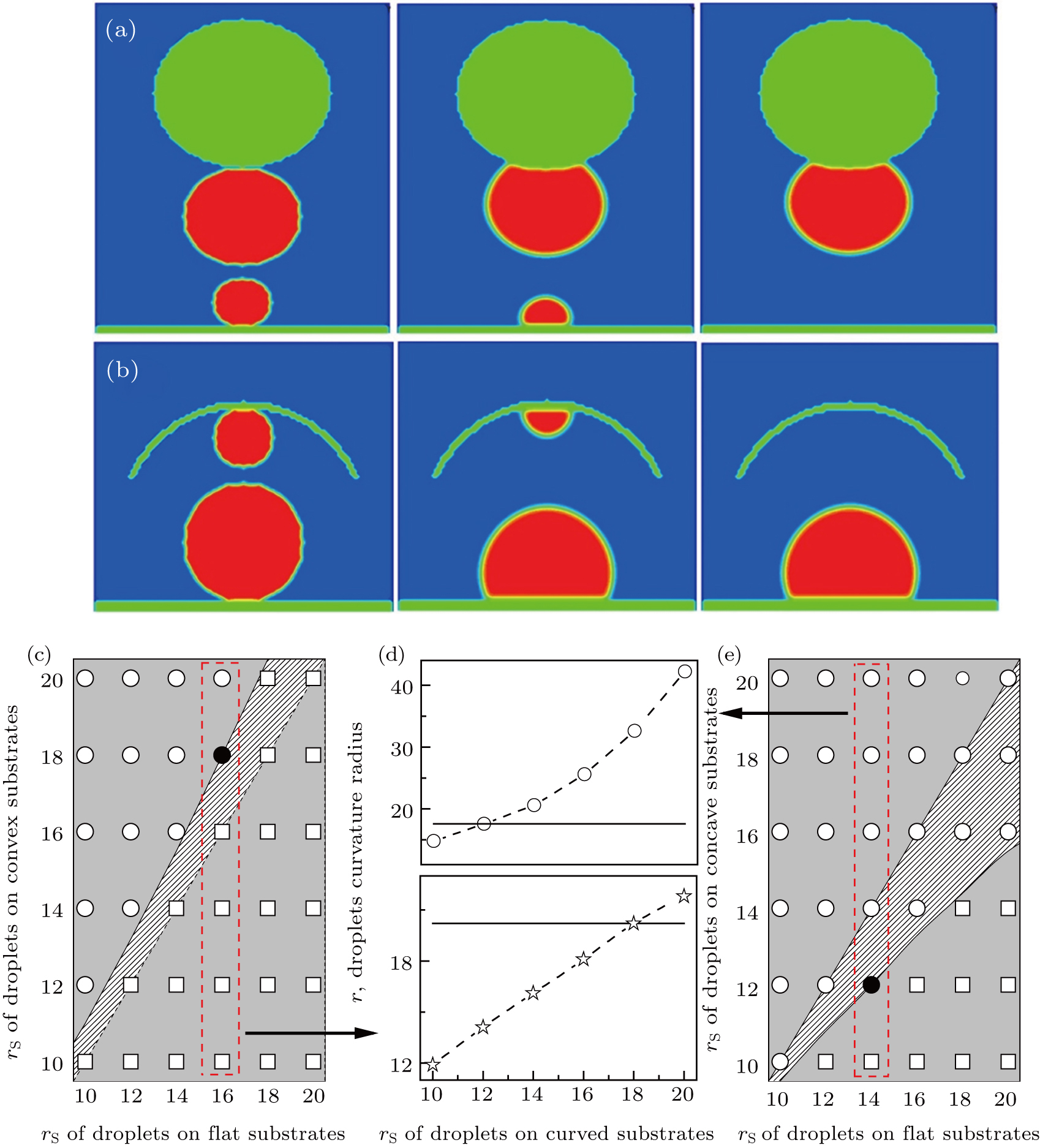
(color online) (a) Liquid transport between the droplet of r_S = 20 on a convex colloid (R = 30) and the droplet of r_S = 10 on a flat substrate. The snapshots correspond to the time steps of 0, 2500, and 4000. (b) Liquid transport between the droplet of r_S = 10 inside a spherical cavity (R = 40) and the droplet of r_S = 20 on a flat substrate. The snapshots correspond to the time steps of 0, 3000, and 5000. In panels (a) and (b), the solid surfaces have a wettability of θ_Y = 11π/18. Phase diagram for the direction of liquid transport via the Ostwald ripening-like pathway for two droplets on (c) a flat substrate and a convex substrate (R = 30) or (e) a flat substrate and a concave substrate (R = 40). The symbol ◸ denotes the corresponding simulation results for the liquid transferring toward the flat substrate, while the symbol ◯ for liquid transferring towards the curved substrate. To summarize the simulation results, the regions colored in light gray denote the simulated direction for liquid transferring from smaller droplets to larger droplets, while the shaded regions denote a reverse direction from larger droplets to smaller droplets. Note that the reverse transport towards the droplet of a smaller r_S does not mean the liquid transport towards the sessile droplet with a smaller curvature radius r. The symbol • shows the simulation results without apparent liquid transport during the simulation runs. (d) The radius of curvature for droplets on the curved substrates (measured before the transport begins), r, as a function of r_S, which was used to represent the droplet volume: (top) for droplets on concave substrates that are denoted in panel (e) and (bottom) for the droplets on convex substrates that are denoted in panel (c). As a comparison, solid lines in panel (d) show the curvature radii for the corresponding droplets on flat substrates. The solid substrates in panels (c)–(e) have a wettability of θ_Y = π/2.