Project supported by the National Natural Science Foundation of China (Grant Nos. 11704266 and 11774245), the Fok Ying Tung Education Foundation, China (Grant No. 151010), the Scientific Research Base Development Program of Beijing Municipal Commission of Education, China, the General Foundation of Beijing Municipal Commission of Education, China (Grant No. KM201810028006), and the Training Program of the Major Research Plan of Capital Normal University, China.
Project supported by the National Natural Science Foundation of China (Grant Nos. 11704266 and 11774245), the Fok Ying Tung Education Foundation, China (Grant No. 151010), the Scientific Research Base Development Program of Beijing Municipal Commission of Education, China, the General Foundation of Beijing Municipal Commission of Education, China (Grant No. KM201810028006), and the Training Program of the Major Research Plan of Capital Normal University, China.
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11704266 and 11774245), the Fok Ying Tung Education Foundation, China (Grant No. 151010), the Scientific Research Base Development Program of Beijing Municipal Commission of Education, China, the General Foundation of Beijing Municipal Commission of Education, China (Grant No. KM201810028006), and the Training Program of the Major Research Plan of Capital Normal University, China.
Surface plasmon polaritons (SPPs) are evanescent waves propagating along metal–dielectric interfaces, which provide an effective way to realize optical wave guiding with subwavelength confinement. Metallic nanostructures supporting SPPs, that is, plasmonic waveguides, are considered as required components to construct nanophotonic devices and circuits with a high degree of miniaturization and integration. In this paper, various types of plasmonic waveguides operating in the visible, infrared, and terahertz regions are reviewed, and the status of the research on their fundamentals, fabrications, and applications is provided as well. First, we discuss the mechanisms of SPPs beyond the diffraction limit, and their launching methods. Then, the characteristics of SPPs on various plasmonic waveguides are reviewed, including top-down and bottom-up fabricated types. Considering applications, certain prototypes of plasmonic devices and circuits constructed by plasmonic waveguides for bio/chemo sensing, router, and light modulation are demonstrated. Finally, a summary and future outlook of plasmonic waveguides are given.
An optical waveguide is a kind of dielectric microstructure which can confine the propagation of optical waves in one or two dimensions with minimal energy loss. Owing to their unique advantages in information transmission, such as high speed, large capacity, and anti-interference, optical waveguides have been crucial components in photonic circuits performing optical signal guiding,[1] coupling,[2] switching,[3] splitting,[4] multiplexing,[5] and so on. To fulfill the increasing demand for information processing and computing, several efforts have been devoted to the miniaturization and high-density integration of photonic circuits. However, the diffraction limit of light restricts the size of dielectric optical waveguides, that is, half of the effective wavelength.[6] Fortunately, surface plasmons, which are collective electron oscillations of noble metal nanostructures, provide an effective approach to address the problems of the diffraction limit.[7–10] When light couples with metal nanostructures, the excitation of surface plasmons can transform the free-space light into plasmon modes, which are highly confined at the metal surface, enabling light manipulation at nanometer scale. Depending on the dimensions of the confinement, excited surface plasmons can be categorized as localized surface plasmons resonances (LSPRs) and propagating surface plasmon polaritons (SPPs). LSPRs are typically excited in nanostructures which are significantly smaller than the incident wavelength, such as nanoparticles and their coupling geometries,[11–15] and have important applications in ultrasensitive detection and sensing.[16–19] SPPs are propagating electromagnetic waves with their field tightly confined at the interfaces between metals and dielectrics,[20–23] similarly to light guided by optical fibers. In this review, for the purpose of information transmission and ultra-compact photonic circuits integration, only the propagating SPPs with subwavelength confinement are considered. So far, various metallic nanostructures have been fabricated to support SPPs, known as plasmonic waveguides, such as thin metal films, insulator/metal/insulator slabs, metal/insulator/metal slabs, metal stripes, metal grooves, or chemically synthesized metal nanowires (NWs). These plasmonic waveguides have been considered to be among the best components to construct the nanophotonic devices to realize light manipulation at nanometer scale, and certain simple plasmonic circuits have recently been accomplished.[24–30]
In this review, our aim is to present various plasmonic waveguides operating at visible, infrared and terahertz regions and to provide the status of the research on their fundamentals, fabrications, and applications. We begin with a discussion of the fundamentals of SPPs beyond the diffraction limit in Section
In dielectric waveguides, optical waves are confined and guided by the total internal reflection at the dielectric interface. The dispersion relation of light propagating in dielectric waveguide with an angular frequency ω can be expressed as
 |
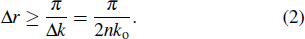 |
Nevertheless, by comparing with the spatial light in the dielectric waveguide, the dispersion relationship of SPPs propagating along the dielectric-metal interface is significantly different. As shown in Fig.
 |
 |
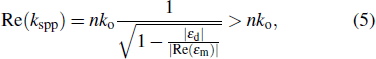 |
As photonic components, the SPP-based plasmonic waveguides are expected to be able to interface with the real optical environment; however, the wavevector of SPPs is larger than that of free space light. Therefore, special experimental arrangements need to be designed to ensure the necessary wavevector conservation during the conversion of photons to surface plasmons. A typical method to launch SPPs at the metal–dielectric interface is to employ the attenuated total reflection in the Kretschmann configuration (prism coupling),[32] which allows the matching of the SPPs wavevector with the parallel component of light wavevector (Fig.
 | Fig. 2. (color online) SPP excitation configurations. (a) Kretschmann configuration for prism coupling, reproduced from Ref. [32]. (b) Diffraction on a grating structure, reproduced from Ref. [33]. (c) Scattering on nanowire termination, reproduced from Ref. [38]. (d) Excitation by near-field end-fire configuration, reproduced from Ref. [39]. |
Except for light excitation, SPPs can be directly launched by electrons.[41] For a focused electron beam, the electric field around the moving electrons contains Fourier components of all frequencies; therefore, plasmons at different frequencies can be excited simultaneously due to the Coulomb interaction, as shown in Fig.
 | Fig. 3. (color online) Excitation of SPPs on an Au nanowire by electrons (100 keV). Left panel: Probability of energy-loss of electrons passing at a distance of 10 nm from the surface of a free-standing Au nanowire. Right panel: EELS probability integrated over parallel momentum (solid curve) and partial contributions of SPP modes (dash lines), reproduced from Ref. [41]. |
SPP-based waveguides allow light to be concentrated into regions as small as a few nanometers, limited only by the atomic structure of matter, propagation loss, and the dispersion relation. Based on the fabrication methods, plasmonic waveguides can be categorized into top-down fabricated and bottom-up fabricated types.
The top-down approach refers to the nanofabrication method starting from bulk materials and subsequently using finer tools to create the designed nanostructures. Currently, the most commonly used nanofabrication techniques for metal nanostructures are electron beam lithography and focused ion beam milling.[42–44] By exploiting the development of nanofabrication techniques, the precise control over metal patterns at nanometer scale has been accomplished, which significantly accelerates the fundamental studies and practical applications of metal plasmonics.[45–47] In this section, we focus on the review of top-down fabricated plasmonic waveguides, such as metal stripes, grooves, and ultrathin corrugated metal strips.
A metal stripe refers to a symmetric thin metal film (with a typical thickness below 100 nm) with its width customized from the micron to the nanometer scale. Pierre Berini discussed the dispersion characteristics of SPP modes on metal stripes first, which provided the fundamentals to use them as plasmonic waveguides.[48] Generally, SPPs on these metal stripes can be launched by a prism-coupling arrangement, as described in Section
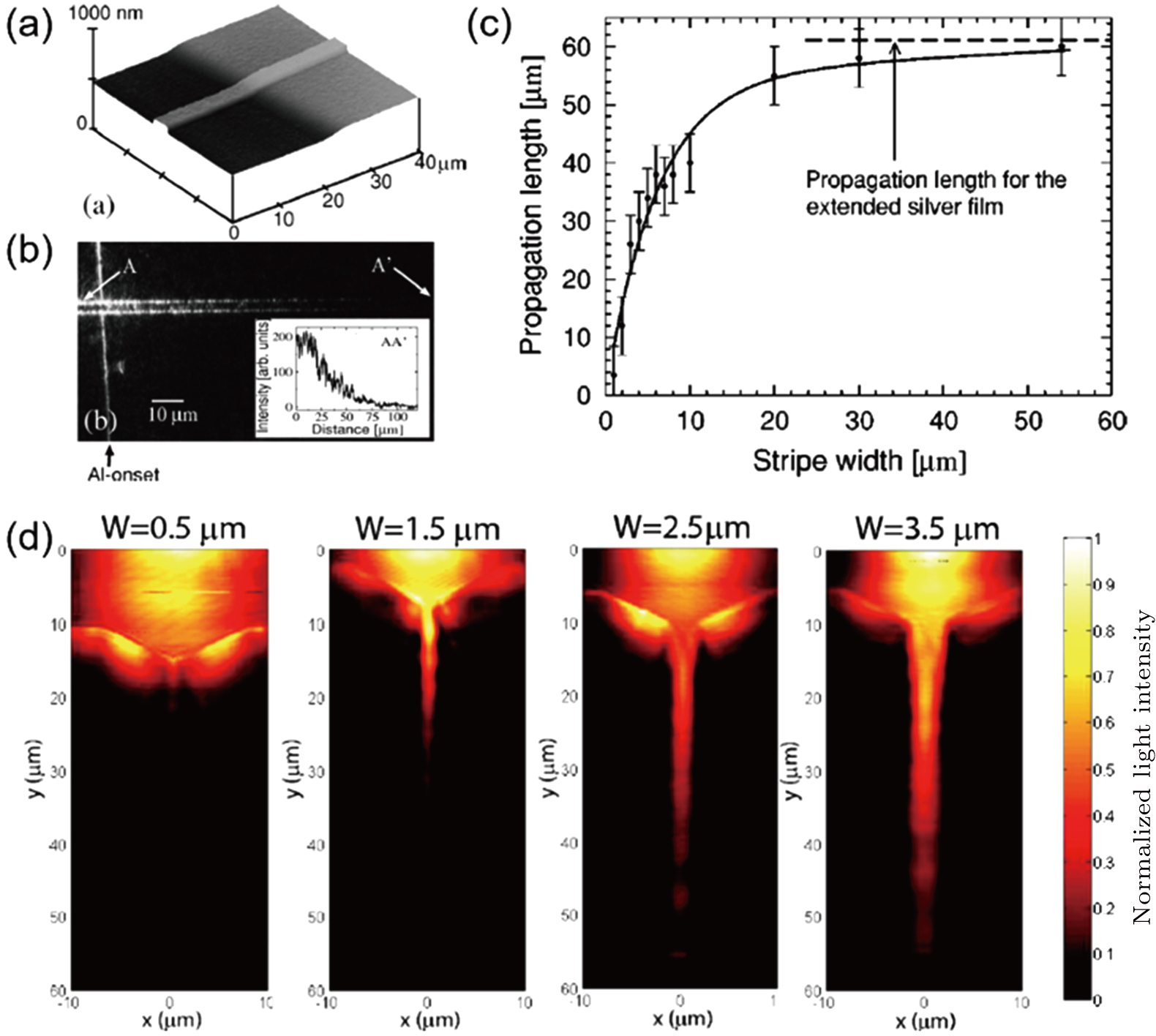 | Fig. 4. (color online) (a) The atomic force microscope (AFM) image of a 3-μm-wide and 70-nm-thick silver stripe. (b) Far-field scattered light image of an SPP propagating in the silver stripe. The inset shows the 1/e propagation length. (c) LSPP in 70-nm-thick silver stripes as a function of stripe width (λ = 633 nm), reproduced from Ref. [49]. (d) Near-field PSTM images of surface plasmons propagating along gold stripes with different widths (λ = 780 nm), reproduced from Ref. [51]. |
Besides the LSPP, another unusual feature of SPPs propagating along a metal stripe is their strong lateral confinement within the stripe width. In order to study this behavior, stripes of different widths attached to a gold thin film are fabricated by electron beam lithography (Fig.
 | Fig. 5. (color online) (a) SEM images of 55-nm-thick gold stripes. The widths of the stripes are in the range of 2–4.5 μm in steps of 0.5 μm. (b) AFM and (c) PSTM images of the tapered junction between the extended thin film and the 2.5-μ m-wide stripe shown in (a). (d) Transverse cross-cuts of the near-field intensity distribution recorded at a constant height over three of the stripes (widths of 4 μm, 2.5 μm, and 1.5 μm) shown in (a), reproduced from Ref. [53]. |
A metal triangular V-shaped groove is another typical structure, which can be employed as a plasmonic waveguide.[8,54,55] This V-groove configuration can be considered as a special type of gap waveguide (metal–insulator–metal (MIM)), whose width is monotonically decreases with the increase of the depth. For the MIM structure, with a narrow of gap width, the effective indexes of the SPPs modes increase, while the LSPP decreases correspondingly (Fig.
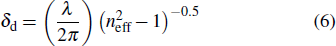 |
 | Fig. 6. (color online) (a) Effective indexes of the gap surface plasmon modes and their propagation length as a function of the width of the air gap between gold films. (b) Effective indexes of the fundamental CPP modes at 1.55 μm and their propagation lengths as a function of the groove depth for different θ groove angles, reproduced from Ref. [56]. |
Nevertheless, the dispersion characteristics of CPP modes (mode index, confinement, and propagation length) were also experimentally investigated by near-field optical microscopy.[59] As can be seen in Fig.
 | Fig. 7. (color online) (a) SEM image of the groove milled in a gold film. (b) CPPs launched by end-fire configuration. (c) Microscope image of the near-field optical probe. (d) SNOM images recorded at different wavelengths, in the range of 1425–1630 nm. (e) CPP dispersion: the CPP propagation length as a function of light wavelength. Insets show the electric field distributions of the fundamental CPP modes at different wavelengths. (f) Optical signal recorded inside the groove as a function of the distance between the probe and the bottom of the groove, together with the exponential fitting curves (dash lines), reproduced from Ref. [59]. (g) Near-field optical images taken at 1600 nm: (I) S-bends and (II) Y-splitter, reproduced from Ref. [62]. |
The metal strip and groove structures mentioned above are SPP waveguides operating at visible and near infrared regions, which demonstrate subwavelength confinement owing to the negative permittivity of metals below the plasmon frequency (Eq. (
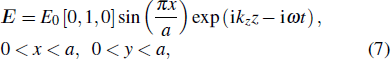 |
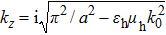
 |
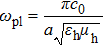
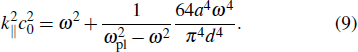 |
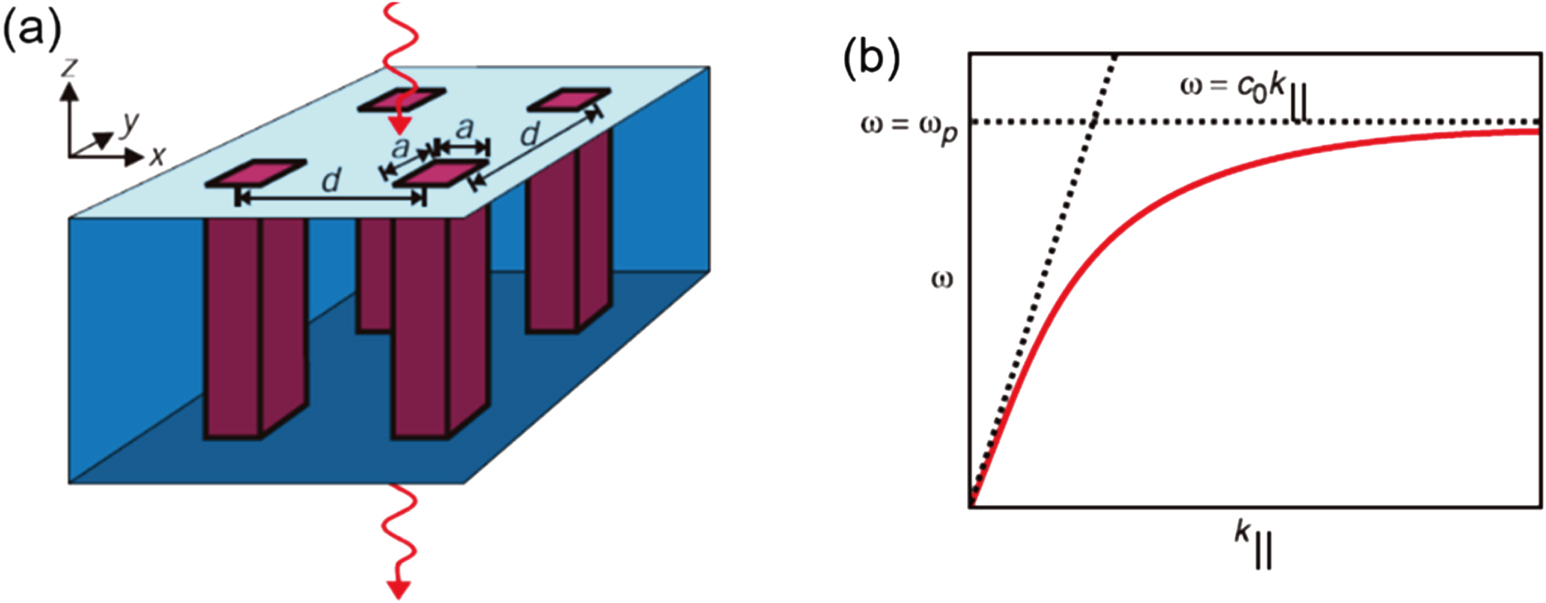 | Fig. 8. (color online) (a) Model of the structured surface with square holes cut into the PEC. (b) Dispersion relation for spoof surface plasmons on the structured surface, with the asymptotes of the light line at low frequencies and the plasmon frequency at large values of k||, reproduced from Ref. [66]. |
So far, several metamaterials have been designed to support spoof SPPs, such as periodically corrugated metal structures[68,69] and Domino structures.[70] To realize highly-integrated SPP waveguides and components, Cui et al. proposed ultrathin periodically corrugated metal strips, which support the spoof SPPs, as shown in Fig.
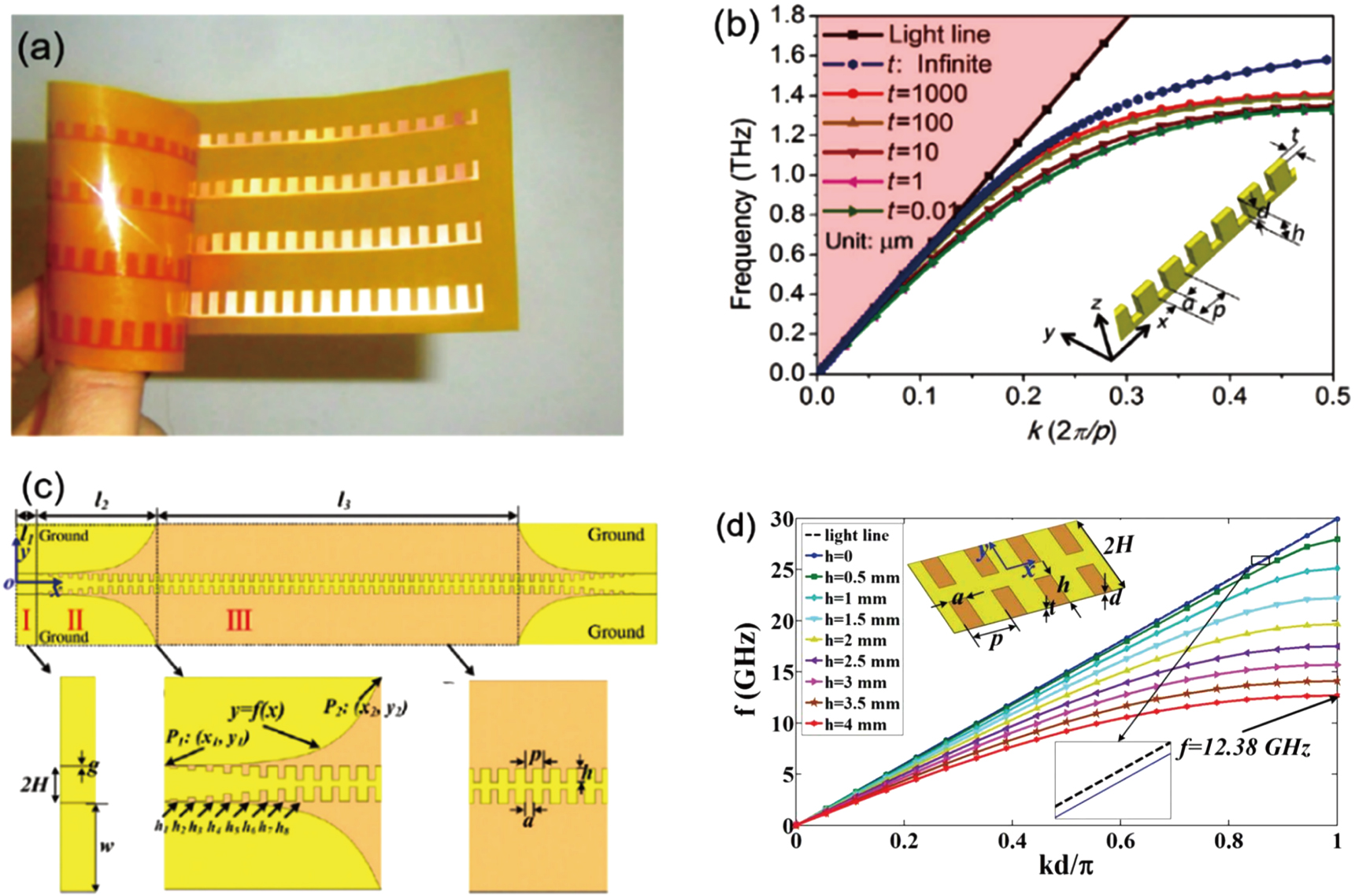 | Fig. 9. (color online) (a) Photograph of the corrugated metal strip fabricated using a flexible copper clad laminate. (b) Dispersion curves of the spoof SPPs in the corrugated metal strips with different thicknesses (t). The black curve describes the light in free space, reproduced from Ref. [72]. (c) Configuration of the CPWs-to-spoof SPPs converter. I: CPW section. II: Matching transition bridge consisting of gradient grooves and a flaring ground. III: Spoof SPP waveguide (ultrathin corrugated metallic strip). (d) Dispersion curves of the ultrathin corrugated metallic strip (t = 18 μm) with different groove depths (h). The black curve describes the light in free space, reproduced from Ref. [74]. |
The bottom-up strategy attempts to build nanostructures from atomic or molecular components, referring mainly to the chemical synthesis. The first reported synthesis of plasmonic metal nanoparticles was performed more than 150 years ago when Faraday prepared Au colloids by reducing Au chloride with phosphorus in solution.[79] The performance of these chemically synthesized metal nanostructures is generally determined by a complex interaction of kinetics and thermodynamics.[80] Recently, shape-controlled synthesis has been accomplished by adding selective capping agents, which can change the order of facets free energies and drive the growth of the nanostructure to the expected shapes, such as sphere,[81] polyhedron,[82] or rod.[83] In this section, we focus on the review of chemically synthesized nanowires and nanobelts, which can perform as excellent plasmonic waveguides.
Comparing with the top-down fabricated waveguides, chemically synthesized metal nanowires can guide SPPs at visible regions with a significantly lower propagating loss owing to their unique single crystalline structure and atomically smooth surface. A convenient method to synthesize metal nanowires is to use a polyol process using poly(vinylpyrrolidone) (PVP) as the coordination reagent.[84] The PVP molecules can selectively cover the {100} facets and allow the {111} facets grow preferentially; thus, forming a one-dimensional nanowire structure (Fig.
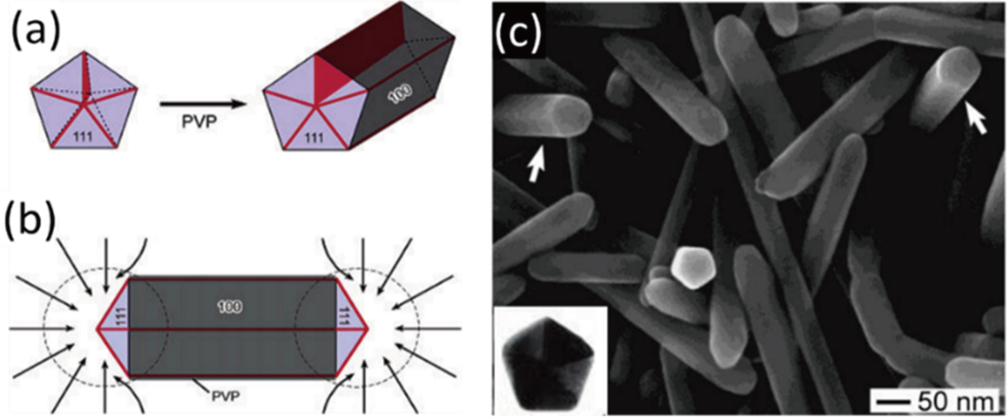 | Fig. 10. (color online) Mechanism of nanowire synthesis. (a) Evolution of a nanowire from a multiply twinned nanoparticle. The ends of this nanowire are terminated by {111} facets and the side surfaces are bounded by {100} facets. (b) Diffusion of silver atoms toward the ends of the nanowire, with the side surfaces completely passivated by the PVP. (c) SEM images of the silver nanowires. The inset is a TEM image of the nanowire cross section, reproduced from Ref. [84]. |
On the synthesized nanowire, multiple SPP modes with different propagation characteristics can be launched. For a cylindrical metal nanowire model, the electric field of the different plasmon modes can be written in cylindrical coordinates as
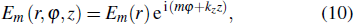 |
 | Fig. 11. (color online) (a) Schematic illustration of an SPP propagating on a nanowire. The excitation beam with electric field E and polarization angle θ is focused on the nanowire end. (b) Field distribution of the four lowest-order SPP modes propagating on the nanowires, reproduced from Ref. [85]. |
 | Fig. 12. (color online) (a) Fluorescence images of SPPs propagating on a Ag nanowire. (i) Optical image of the nanowire. (ii)–(iv) Polarization-dependent fluorescence images of the SPPs, reproduced from Ref. [85]. (b) SEM image of Ag nanowires. (c), (d) Raman imaging of the structure in (b) with left circular polarization (c) and right circular polarization (d), reproduced from Ref. [88]. |
Owing to the atomically smooth surface and well-crystalline structure, the scattering loss and ohmic damping of the propagating SPPs can be greatly reduced and the LSPP on the synthesized nanowires can reach up to tens of micrometers. These robustly propagating SPPs can be reflected effectively by the wire end faces, and the interference between the incident and reflected SPPs can create a standing surface plasmon wave along the nanowire axis, indicating that the metal nanowires can be used as an SPP Fabry–Pérot resonator. Krenn et al. reported an SPP Fabry–Pérot resonator of synthesized nanowires first.[89] They investigated non-radiating surface plasmon modes on silver nanowires by SNOM mapping, with wavelengths shortened to approximately half of the exciting light, as shown in Fig.
 | Fig. 13. (color online) (a) Illumination of optical excitation: I denotes the input and D is the other end of the wire. (b) Optical image: the bright spot on the left is the focused exciting light. The arrow indicates the light scattered from the wire end. (c) SNOM image of the SPPs on a nanowire excited by 785 nm. (d) Cross-cut along the chain dotted line in (c), reproduced from Ref. [89]. (e) SEM image of a silver nanowire on a monolayer MoS2. (f) Magnified SHG image at the overlap region when the SPPs on the nanowire are excited at the left end. (g) Calculated SHG intensity at a plane located 1.3 μm from the monolayer MoS2. The scale bar is 2 μm in (e) and 500 nm in (f) and (g). (h) Intensity profiles along the Ag nanowire, corresponding to the dashed lines in (f) and (g), respectively, reproduced from Ref. [90]. |
Recently, Xu et al. discussed the second harmonic generation (SHG) excitation of monolayer molybdenum disulfide (MoS2) by Fabry–Pérot SPP resonance.[90] In general, it is difficult to enhance nonlinear optical processes using SPPs in plasmonic waveguides due to the mismatch in momenta. However, the parallel momentum of the propagating SPPs on the nanowires can vanish as the counter of incident and reflected SPPs, which allows the matching of momenta between the SHG photons and the SPPs. It was demonstrated that the generated SHG signals were emitted in the direction perpendicular to the nanowires. Figure
The Fabry–Pérot nature of the SPPs propagating on the nanowire can highly affect the direction of the emission of the SPPs at the wire ends. Li et al. measured the spatial distribution of the nanowire emission for the first time.[38] By gradually varying the numerical aperture (N.A.) of the objective, the intensity containing the direction information of the emission of the SPPs can be detected. As shown in Fig.
 |
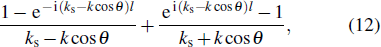 |
 | Fig. 14. (color online) (a) Referred coordinates. The wavevector and polarization of the excitation light are represented by the red arrows. The N.A. corresponds to the opening angles of the collection cone. The emission from the wire end is collected by an objective. (b) Calculated emission intensity as a function of angles ϕ and θ. The inset shows the corresponding angular distribution on the integration sphere, reproduced from Ref. [38]. |
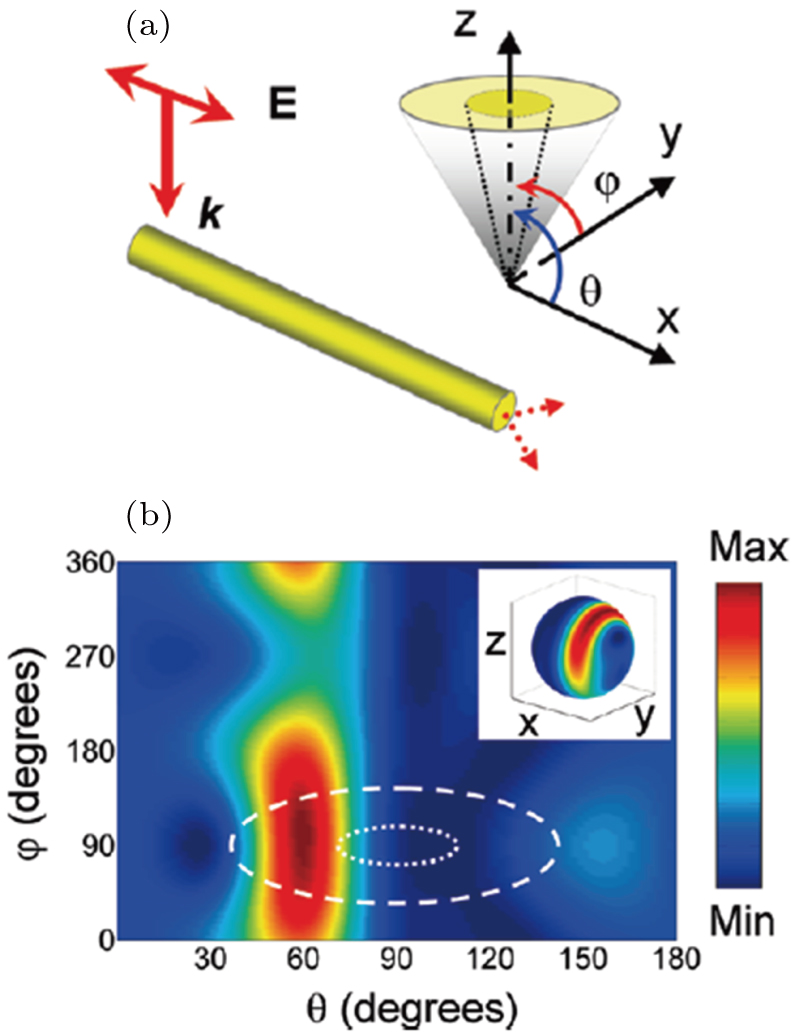
Synthesized metal nanobelt structures, similarly to the nanowires with rectangular cross section, can also be used as excellent plasmonic waveguides. Qi et al. reported gold nanobelt synthesis with a surfactant mixture of cetyltrimethylammonium bromide (CTAB) and sodium dodecyl sulphate (SDS).[91] It was revealed by SEM, high-resolution TEM, and diffraction pattern measurements (Figs.
 | Fig. 15. (color online) (a) SEM image of a gold nanobelt. The sample was tilted by 45° to reveal the rectangular cross section. (b) High-resolution crystalline structure of the nanobelt. (c) Electron diffraction indicates the single-crystalline gold structure, reproduced from Ref. [91]. (d)–(e) Calculated field intensity of a 125 nm × 40 nm gold nanobelt for the m = 0 (d) and m = 1 (e) modes, reproduced from Ref. [92]. (f) SPP scattering peaks at different cross section aspect ratios in experiments (black) and simulations (white), reproduced from Ref. [93]. |
SPP waveguides exhibit a unique capacity to concentrate and manipulate light in deep subwavelength regions, which makes them particularly useful for the future design and development of integrated nanophotonic devices and circuits. In the following section, certain functional plasmonic components and devices, which have been developed with SPP waveguides, are introduced.
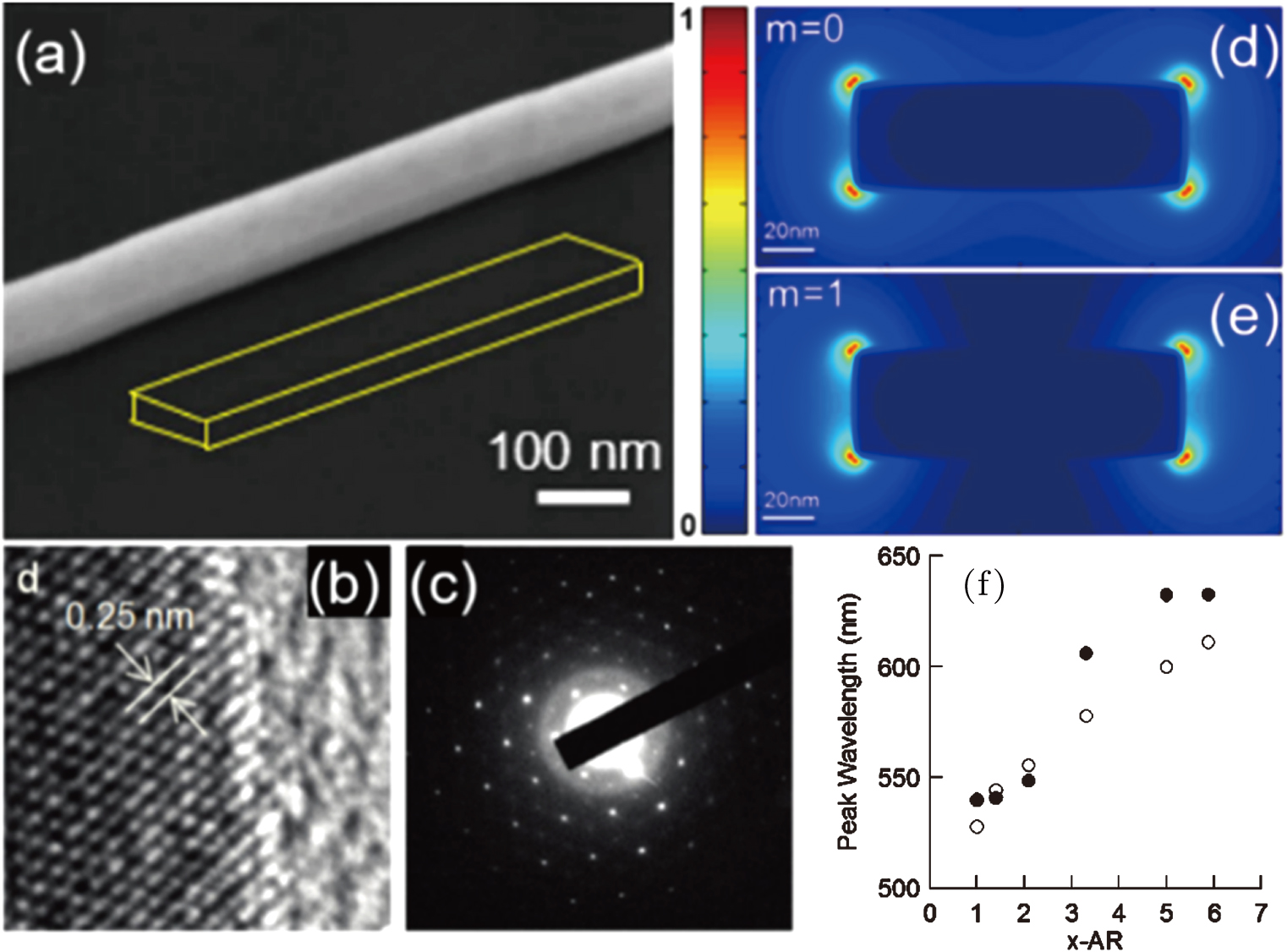
As it is well known, the LSPR frequency strongly depends on the size and shape of the particles and the dielectric constant of the surrounding medium.[94–96] By varying these parameters, the resonances can be tuned over the visible and mid-infrared regions. Thus, the LSPR of metal nanostructures can be used as an effective sensor, as it has been demonstrated in such promising applications as chemical identification[97–99] or biological detection.[100–102] Compared with nanoparticles, SPP waveguides can be used as a sensor with several unique advantages, which cannot be achieved simply by LSPR; thus, it has been attracting increasing attention in recent years. A typical advantage is that the larger scattering cross section provided by the waveguides can allow ultrasensitive detection of the changes in the environment, especially with some SPP cavity modes confined in a deep nanoscale area. Xu et al. recently reported the sensing of vertical dimensional variations by a nanowire-on-mirror system.[103] The structures are shown in Figs.
 | Fig. 16. (color online) (a) Coupled metal nanowire and mirror system. The change in thickness of the separating layer can be precisely detected. (b) High-resolution TEM image of the cross section of the nanowire and mirror system. The scale bar is 30 nm. (c) Calculated scattering spectrum of a 45-nm-diameter Au nanowire on a gold film with 2 nm separation. (d) Measured resonant peak of the cavity plasmon mode as a function of the Al2O3 layer thickness, reproduced from Ref. [103]. (e) Remote excitation SERS of a live HeLa cell by Ag nanowire. (f) SEM image of a typical tungsten tip with Ag nanowires attached. (g) Magnified image of the probe tip, reproduced from Ref. [104]. (h) Schematic of the experimental setup, showing the integration of the nanofocusing remote SERS sensor into an AFM microscopy, reproduced from Ref. [105]. |
 | Fig. 17. (color online) (a) Nanowire networks as an optical logic gate. Diagram of a NOR logic gate built using cascaded OR and NOT gates (upper) and optical image of the designed structure (lower), reproduced from Ref. [107]. (b) (i) Optical image of a nanowire network with two input terminals (I1 and I2) and two output terminals (O1 and O2). (ii) and (iii) QD fluorescence images for two phase differences corresponding to the strongest output at terminal O1 and O2, respectively, reproduced from Ref. [108]. (c) SPP router by SOI of light, reproduced from Ref. [109]. (d) and(e) SPP wave router using V-groove, reproduced from Ref. [64]. (f) Image of a spoof SPP router. (g) and (h) Spoof SPP field measured on the router of (f), reproduced from Ref. [76]. |
Nevertheless, the SPP waveguides can support remote chemical sensing, which can prevent any modification or destruction to the analytes by direct illuminations, especially in living systems. Uji-i et al. recently reported a living cell remote-excitation surface-enhanced Raman scattering (SERS) detection by a nanowire-nanoparticle coupling system (Fig.
For an integrated plasmonic chip with both electronic and SPP components, a router is necessary as a BUS to process the signals. In an electronic circuit, besides the on and off states, a third state of no input is needed, so that the signals can be exchanged without being disturbed by other components. As metal nanowires can simultaneously support different SPP wavelengths and can manipulate them independently, they become suitable choices for a router in plasmonic circuits.[106] In particular, by changing the polarizations of the excitation light, the mode components and field distributions on the nanowires can be manipulated, as discussed in
An SPP router with a nanowire network can be implemented by employing the varied phase difference of SPP modes interference.[107,108] As shown in Fig.
A broad dynamic range of light absorption in the plasmonic structures opens the possibility for the efficient all-optical modulation of SPP transmission. Recently, for planar nanostructures, electro-optical modulation light transmission by a multimode interference in a plasmonic waveguide has been realized.[110,111] However, in the above examples, the modulation was achieved using planar SPP modes, which are less confined in the lateral direction and cannot realize a high-degree on-chip integration.
Recently, Li et al. reported that a highly-confined SPP modulator can be implemented using nanowire structures.[112] Figure
 | Fig. 18. (color online) (a) SEM image of a nanowire structure as SPP modulator. (b) and (c) Optical images of the branch excited by two coherent 633-nm laser spots at inputs 1 and 2, respectively. The phase difference of the two SPPs at output 3 is Δ = 0°(b) and 180°(c), reproduced from Ref. [112]. |
In summary, we briefly reviewed the characteristics of various SPP waveguides operating in visible, infrared, and terahertz regimes. The dispersion relation reveals that the SPP wavevector is larger than that of free space light at the same frequency, which permits the subwavelength confinement beyond the diffraction limit. So far, various plasmonic waveguides have been fabricated by top-down and bottom-up methods, such as metal stripes, grooves, nanowires, and periodically corrugated surface, which can be crucial building-blocks to construct next-generation photonic devices with high-density integration. Certain simple plasmonic devices and circuits have been accomplished for applications, such as ultrasensitive sensing, BUS router, or light intensity modulation. In spite of the advancement in the research of functional elements, there are still several difficulties restraining the achievement of nanophotonic devices and circuits for real applications, such as the issues about the trade-off between the propagation length and confinement, bending loss, and the interface between the plasmonic and electronic circuits. With the further development of nanofabrication techniques, we can anticipate highly-integrated plasmonic circuits, which can be used for practical information transmission and processing, to be available in the near future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] |


