The Goos–Hänchen (GH) shift is usually a tiny lateral displacement from the prediction of geometrical optics when a light beam is reflected from an interface between media.^[1–3] In the past twelve years, the GH shift has been widely discussed in various fields, such as optics,^[4–7] chemistry,^[8] and biomedicine.^[9] The GH shift is usually studied at the interface of structures containing two homogeneous materials with different optical characteristics, and the magnitude of the shift is very small in this case, almost comparable to the wavelength of the incident beam.^[10] Obtaining a large GH shift for better measurement, research, and application has become a hot topic of research. Owing to the noteworthy features of the amplified GH shift, it is often used in designing many devices such as optical switches,^[11] polarizers,^[12] lasers,^[13] absorbers,^[14] sensors,^[9] and filters.^[15]

Researchers have made great progress during the past few decades in studying how to increase the GH shift. For example, large positive and negative GH shifts can be obtained in waveguide structures owing to excitation of waveguide modes.^[16] Further, when light is incident on left-handed materials, a large GH shift occurs owing to resonant excitation of surface vortexlike polaritons,^[17] and external reflection of electromagnetic radiation in anisotropic crystals around its optical phonon frequencies causes a GH shift.^[18] On the other hand, exciting surface plasmons (SPs) is another effective method to enhance the shift. When SPs are excited at a metal–dielectric interface, the electromagnetic fields near the interface become very strong,^[19–23] which can lead to a huge shift. The largest lateral shift observed in experiments is almost 50 times the wavelength of the incident beam.^[24] The method proposed by Chen et al.^[25] using long-range surface plasmon resonance can increase the GH shift to 700λ (where λ is the wavelength of the incident beam), which is almost on the order of millimeters. Since then, SP excitation has been widely used to increase the GH shift.^[26,27] To stimulate SPs, gold and silver are generally chosen as the best noble metal. However, there are still challenges involved in the use of traditional noble metals; for example, it is hard to tune the SP resonance owing to their strong stability, and the propagation distance of SPs is finite owing to the large loss, which limits their flexibility in future applications.

With the development of science and technology in recent years, a variety of new materials has emerged.^[28–32] Graphene, as a new type of two-dimensional material, has attracted a great deal of attention owing to its extraordinary properties,^[33–35] such as high electron mobility, low ohmic loss, high surface area, and adjustable Fermi energy level. Therefore, graphene is used to replace traditional metals to excite stronger SPs and to achieve a controllable GH shift by adjusting the Fermi levels.^[36–38] In addition, because graphene can support p-polarized SPs at infrared and terahertz (THz) frequencies,^[39] Farmani et al. were able to obtain the largest GH shift to date, 1089λ, in the THz range.^[37]

With further research on graphene SPs, manipulation of the optical bistability (OB) has become a hot research topic because of the potential capabilities of controllable graphene SPs. OB occurs in a certain resonant optical structure, which depends on the history of the input light intensity; thus, there are two stable transmission states for a single input light intensity.^[40] OB has become one of the most active research topics in nonlinear optics owing to its potential applications in optical memory,^[41] optical transistors,^[42] optical information processing,^[43,44] and so on.^[45,46] Although tunable GH shifts at THz wavelengths have been reported recently, there have been few reports of the bistable GH shift at THz wavelengths. Thus, in this article, we study the bistable behavior of the GH shift in the THz range; the proposed structure is based on the modified Otto configuration, where graphene covers a nonlinear substrate. We demonstrate that the GH shift can be manipulated by controlling the Fermi level and relaxation time of graphene or the thickness of the air gap. In particular, the GH shift can have positive or negative values and can be enhanced by introducing a nonlinearity in the substrate. The GH shift exhibits bistable behavior owing to the hysteretic behavior of the reflectance phase, which can be manipulated by changing the thickness of the air gap or the Fermi level or relaxation time of graphene.

A modified Otto configuration with highly doped graphene sheets is proposed to excite SPs, as shown in Fig. 1. Here, graphene is coated on a nonlinear substrate with a linear refractive index n₃ of 1.43; high-resistance Si (ε₁ = 11.67) is chosen as the prism, and an air gap (ε₂ = 1) with thickness d is inserted between the Si prism and the nonlinear dielectric material. The transverse magnetic (TM)-polarized light beam is chosen to excite SPs; it is incident from the prism to the nonlinear substrate at an angle θ. A light beam is reflected from the interface between the prism and air gap, and hence a tiny lateral shift S from the prediction of geometrical optics occurs.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Graphene in modified Otto configuration for surface plasmon excitation at THz frequencies. A beam is incident on the structure with incident angle θ, giving rise to a reflected wave with the GH shift S.

Graphene is characterized by a complex surface conductivity σ.^[47] In the THz range, intraband scattering is dominant in highly doped graphene; hence, σ_intra is sufficient to calculate the surface conductivity σ of graphene owing to the limit ωτ ≪ 1,

The reflection coefficient and transmission coefficients can be calculated using the Fresnel formula; however, owing to the nonlinear effects and the effect of graphene on the boundary conduction, the ordinary Fresnel formula should be modified at the interface between the air gap and the graphene covering the nonlinear dielectric. On the basis of our previous work,^[49] r₂₃ and t₂₃ can be written as

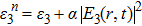
First, if the incident power is low, the nonlinearity of the substrate is not significant; hence, we can ignore the role of the nonlinearity in the GH shift, as shown in Fig. 2(a). Obviously, in the absence of graphene, SPs cannot be excited because the dispersion relation for SPs between the two dielectrics cannot be satisfied. However, the introduction of graphene sheets will afford negative permittivity; hence, the SP condition can be satisfied, and SPs are excited by the TM-polarized incident beam, as shown in Fig. 2(a). In the absence of graphene, total reflection always occurs if the incident angle θ is greater than θ_cr (where θ_cr is the critical angle), and the phase change is small with the increasing incident angle. If we introduce graphene onto the substrate, a reflection dip appears owing to SP excitation. Moreover, the thickness of the air gap significantly affects the SPs. If we increase the thickness of the air gap from 5.2 to 6.0 μm, the reflectance dip changes very little; however, the phase change is very significant with a different sign of slope, which leads to large GH shifts with different sign owing to the dependence of the phase on the angle in Eq. (6). As shown in Fig. 2(c), positive GH shifts as large as 250λ are obtained for d = 5.2 μm, and negative GH shifts as large as −300λ are observed for d = 6.0 μm. The above discussion proves that optimization of the SP conditions is important for obtaining the largest phase change slope and smallest reflectance of the SPs, which are advantageous for obtaining large GH shifts.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Dependence of the reflectance (a), phase of the reflection coefficient (b), and GH shift (c) on the incident angle for different air gap thicknesses with and without graphene. Here λ = 100 μm, τ = 500 fs, EF = 0.9 eV, and N = 5.

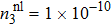
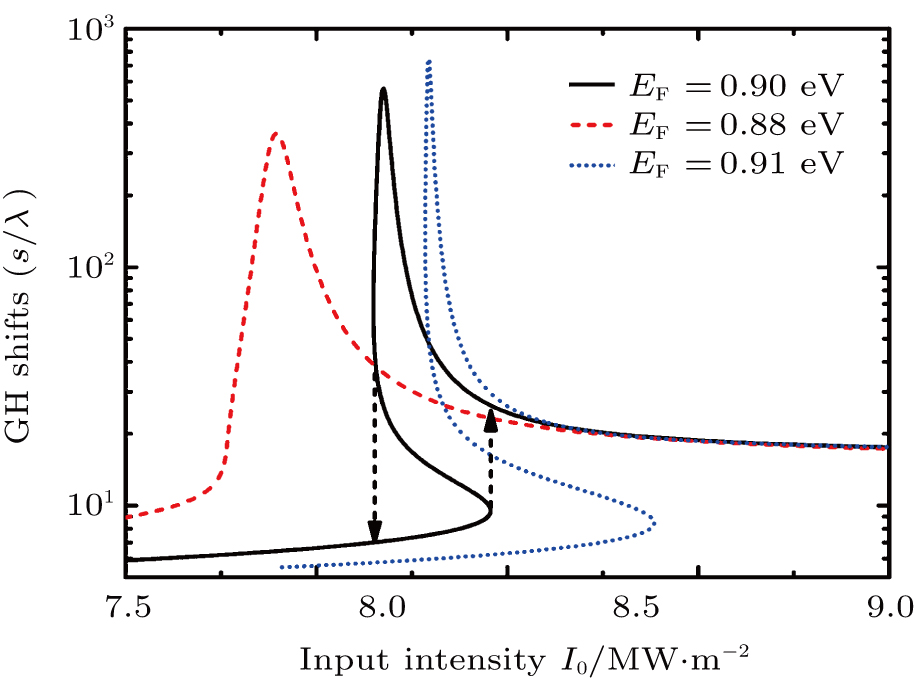
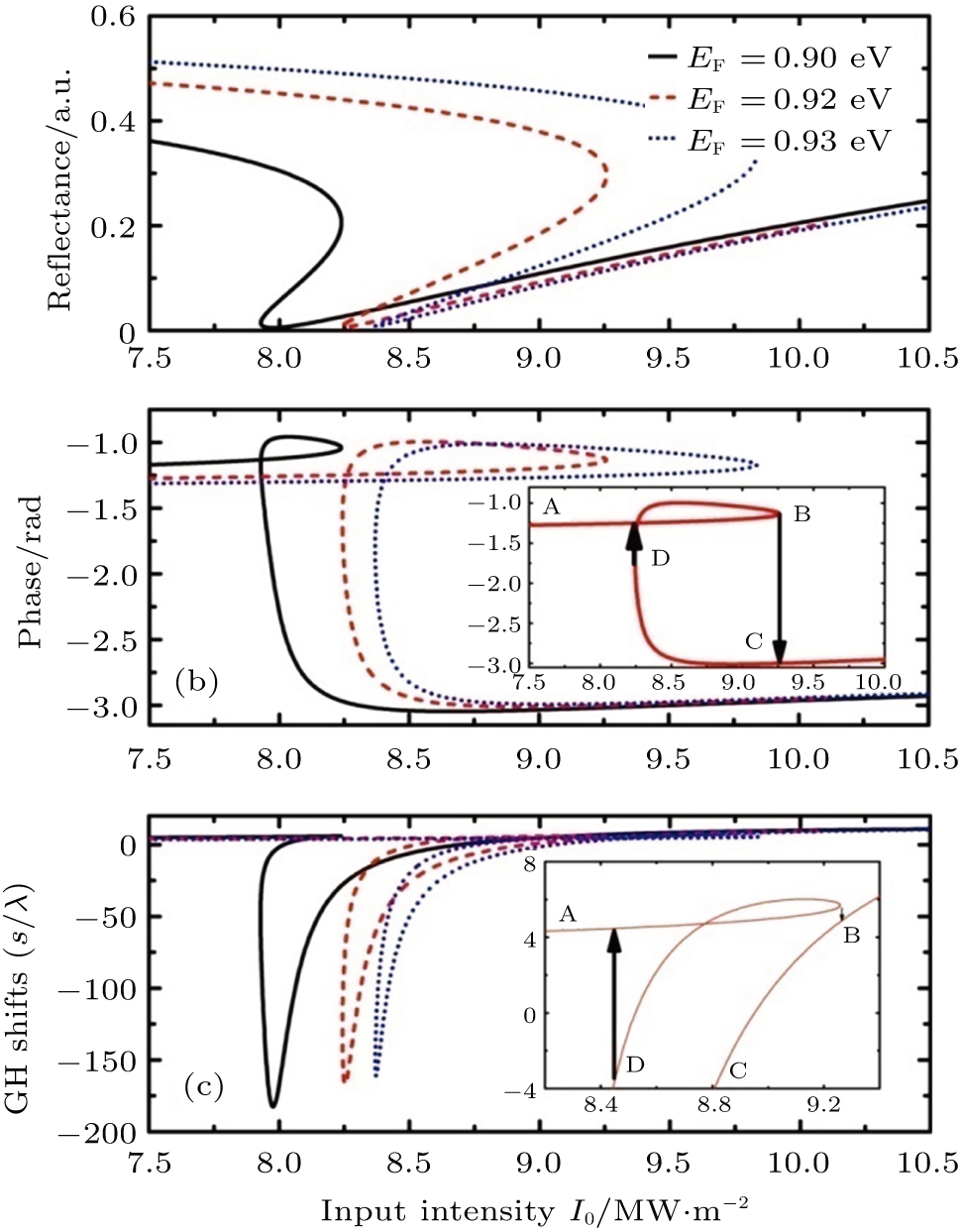
Under strong light excitation, the nonlinear effects will become increasingly important. To obtain a very large nonlinear coefficient ( m²/W), we considered all types of semiconductor materials. We were very fortunate that InSb and GaAs will suffice for our purposes.^[50] To simplify the discussion, we assume that the semiconductor material is nondispersive and n₃ = 1.46. Now, we want to determine the effect of the nonlinearity on the GH shift. Because the GH shift depends on the phase of the reflection coefficient (Eq. (6)), we begin by discussing the nonlinear behavior of the reflectance and its phase. Figure 3 shows the dependence of the reflectance at different Fermi levels of graphene relative to I.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Dependence of the reflectance and reflectance phase on the incident light intensity for different Fermi levels of graphene. Here d = 5.2 μm, θ = 25.44°, and the other parameters have the same values as those in Fig. 2.

For E_F = 0.90 eV, typical S-shaped curves appear for the dependence of the reflectance and the reflectance phase on the incident light intensity. These hysteresis phenomena indicate that two stable output powers can be obtained at a single given input power. As shown in Fig. 3(b), the reflectivity gradually decreases with increasing incident light intensity; however, the reflectivity switches to a very low value if the intensity of the incident light reaches the threshold, I ≈ 8.46 MW/m². In contrast, if we increase the incident intensity, the phase of the reflectance gradually increases, and it can switch from negative to positive values at the threshold, I ≈ 8.46 MW/m². If we reduce I, the reflectance and reflectance phase show opposite bistable reactions to increasing incident light intensity. The relationship between the GH shift and the reflectance phase apparently provides a method to realize low-threshold OB of the GH shift by covering a nonlinear substrate with graphene sheets.

Owing to the strong dependence of the hysteretic effect on the graphene SPs, the optical properties of graphene will play an important role in the bistable behavior of the reflectance and reflectance phase. As we know, the optical conductivity of graphene depends on E_F; hence, E_F will play a large role in the hysteretic effect. As shown in Fig. 3(a), if we decrease the Fermi level to 0.88 eV, there is no hysteresis in the reflectance and its phase owing to the absence of an adequate feedback mechanism. However, if we increase the Fermi level to 0.91 eV (Fig. 3(c)), the switch-up threshold moves to higher I, and the switch-down threshold value is shifted to a lower incident light intensity; hence, the width of the hysteretic loop is enhanced dramatically. As a result, E_F offers an effective route to varying the reflectance phase by controlling the external voltage.

Figure 4 shows the dependence of the GH shift S on the input light intensity I₀ for different values of the Fermi level E_F of graphene sheets, where d = 5.2 μm, and θ = 25.44°. For E_F = 0.90 eV, we see that when I₀ increases from low intensity to the switch-up threshold, I ≈ 8.46 MW/m², the GH shift gradually increases and then suddenly jumps to a large value because the reflectance phase depends on the input light intensity I₀, as shown in Fig. 3(b). However, as I₀ decreases, the GH shift gradually increases, and then a peak appears near the switch-down threshold, I ≈ 8.15 MW/m². Subsequently, the GH shift recovers to its small value with decreasing input intensity. This hysteretic behavior of the GH shift shows that we can enhance it to a large value, S ≈ 560λ, and control it by changing the Fermi level of graphene. If we increase E_F slightly, the GH shift S can be enhanced to a large value, S ≈ 746λ. In fact, we can continue to enhance the GH shift if we are able to increase the Fermi level E_F. However, the hysteretic behavior of the GH shift will disappear, although GH shifts as large as 363λ are still obtained. It is clear that by increasing E_F, we can move the threshold of bistability of the GH shift to higher values, and the bistable loop can be enlarged.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) Dependence of GH shift on the incident light intensity for different Fermi levels of graphene. Here d = 5.2 μm, θ = 25.44°, and the other parameters have the same values as in Fig. 2.

The bistability of the reflectance, reflectance phase, and GH shift also depend on the thickness d of the air gap, as shown in Fig. 5. In Fig. 2(c), we demonstrated that the GH shift will switch from positive to negative values if we increase the thickness d of the air gap from 5.2 to 6.0 μm under lower incident power. Although the reflectance at d = 5.2 μm shows similar behavior to the positive GH shift at d = 6.0 μm in Fig. 4, the reflectance phase shows significant changes and exhibits very intriguing hysteresis (see the inset of Fig. 5(b)). Under these circumstances, the GH shift can be transformed from zero to positive or negative values (see the inset of Fig. 5(c)), and the GH shift also depends on the Fermi level of the graphene sheets.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) Dependence of (a) the reflectance, (b) reflectance phase, and (c) GH shift on the incident light intensity for different Fermi levels of graphene. Here d = 6.0 μm, θ = 25.44°, and the other parameters have the same values as in Fig. 2.

In addition to depending on the Fermi energy, the GH shift is also affected by the electron–phonon relaxation time τ, as shown in Fig. 6(a). When τ increases, the loss of the graphene sheets is decreased, and hence much less light intensity is required to switch the hysteretic behavior of the reflectance phase in the switch-up and switch-down processes. Thus, it is apparent that as the electron–phonon relaxation time increases, both the switch-on and switch-down thresholds are shifted to lower values, indicating that we can decrease the incident intensity to generate the hysteretic effect; however, the peak of the GH shift is suppressed. Furthermore, the bistable GH shift also depends strongly on the air gap thickness, as indicated in Fig. 6(b). Here we choose only positive GH shifts for d < 5.2 μm. It is evident that both the switch-on and switch-down thresholds depend weakly on the air gap thickness; however, the peak value of the GH shift is reduced markedly with decreasing air gap thickness.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) Dependence of the GH shift on the incident light intensity for different electron–phonon relaxation times τ of graphene (a) and air gap thickness d (b). Here d = 6.0 μm, θ = 25.44°, and EF = 0.90 eV in (a), and τ = 0.5 ps, θ = 25.44°, and EF = 0.90 eV in (b), and the other parameters have the same values as in Fig. 2.

In summary, we analyzed the hysteretic response of the GH shift using a modified Otto configuration in which graphene sheets covered a nonlinear dielectric substrate. Our work demonstrated that large positive and negative GH shifts can be obtained by controlling the input light intensity owing to excitation of the graphene surface plasmon resonance. Moreover, we also demonstrated that the bistability of the GH shift depends on the properties of graphene (that is, the Fermi energy and relaxation time) and the thickness of the air gap. The tunability and large GH shift obtained using graphene could pave the way to all-optical switching, optical logic, optical memory, etc.