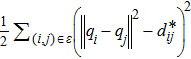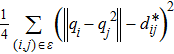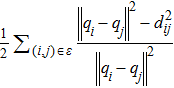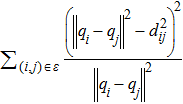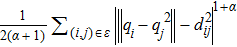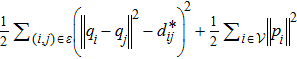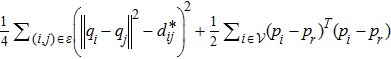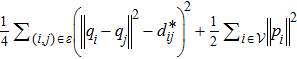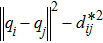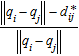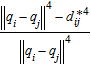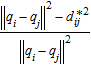Project supported by the National Natural Science Foundation of China (Grant No. 61603188).
Project supported by the National Natural Science Foundation of China (Grant No. 61603188).
† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61603188).
This paper addresses the distance-based formation tracking problem for a double-integrator modeled multi-agent system (MAS) in the presence of a moving leader in d-dimensional space. Under the assumption that the state of leader can be obtained over fixed graphs, a distributed distance-based control protocol is designed for each double-integrator follower agent. The protocol consists of three terms: a gradient function term, a velocity consensus term, and a leader tracking term. Different shape stabilizing functions proposed in the literature can be applied to the gradient function term. The proposed controller allows all agents to both achieve the desired shape and reach the same velocity with moving leader by controlling the distances and velocity. Finally, we analyze the local asymptotic stability of the equilibrium set with center manifold theory. We validate the effectiveness of our approach through two examples.
Over the past decade, formation control of MAS is an active research area in cooperative control and robotics due to its widespread applications in a variety of areas, such as satellite formation flying, search missions using flying agents, cooperative transportation, sensor networks, and so forth.[1,2] The aim of multi-agent formation control is to drive a group of agents to achieve and to maintain a desired graphic pattern with (or without) references.
As reviewed in Ref. [3], the existing control strategies for multi-agent formation control can be classified into position-based, displacement-based, and distance-based strategies. Among these formation strategies, distance-based control strategy assumes that agents sense and control the relative distance of their neighboring agents, which allows the reduced requirements for the sensing capabilities for each agent. In other words, compared with the other two strategies, the main advantages of the distance-based control lie in that agents need less global information and do not require expensive sensors.
We focus only on works based on distance-based formations in this paper. A gradient control law based on the potential function was proposed in Refs. [4] and [5], and the target undirected formation was defined by a set of inter-agent distances. After that, the authors in Ref. [6] extended the result in Ref. [5] to n-dimensional space and proposed gradient-based formation controllers for single-integrator and double-integrator modeled agents. A unified approach formation controller with general forms of gradient functions was developed in Ref. [7] to guarantee the exponential stability of the distance-based rigid formation control MASs. In Ref. [8], the authors considered the formation tracking problem under a rigidity framework for single-integrator modeled MAS. Among the aforementioned literature, one common feature is that the controllers employ objective functions to share shape control tasks between agents. Designing a potential function is a good way to show the constraint relation between each agent in the formation and easy to achieve real-time control.
Note that the results above primarily concentrate on the ideas of distance-based formations for single-integrator modeled agents. The research on distance-based control of double-integrator modeled agents has attracted attention, but most of them require the velocities of agents to decay to zero (e.g., Refs. [6] and [9]). Motivated by the pioneering work,[10] recent papers[11,12] combined the flocking strategy and the distance-based shape control strategy so as to show that the desired formation of double-integrator modeled agents can be achieved while all agents share a common velocity. As listed in Table
| Table 1.
Review of distance-based undirected formation with gradient-flow method. . |
Therefore, the motivation is to develop a new formation tracking control strategy with a gradient function for followers. The gradient function will be considered as a general form which can encompass the most distance-based shape stabilizing controllers with different forms proposed in the literature. The main contributions of this paper can be summarized as follows. Firstly, a procedure to design distance-based control laws for the formation tracking problem will be constructed. We will give a characterization of shape stabilizing gradient functions for undirected distance-based formation and list the required conditions for distributed gradient-based controllers over a given undirected graph 
This paper is organized as follows. Section
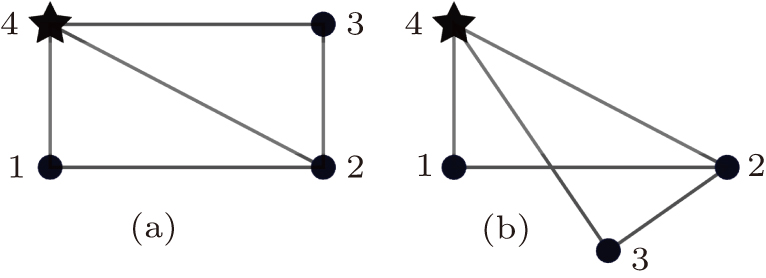
An undirected graph with n agents and m edges is denoted by 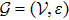

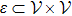
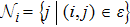
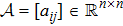


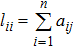
Consider n single-integrator modeled agents in d-dimensional space
A graph that has a unique realization cannot be susceptible to continuous flexing and must be rigid.[25] A detailed discussion of graph rigidity can be found in Ref. [25]. One useful tool to characterize some other concepts related to graph rigidity is the rigidity matrix Jgq(q). We define the rigidity function associated with the framework 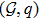
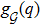
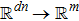
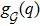
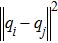
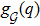
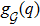
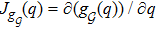
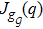
Let q* ∈ ℝdn be given. Let 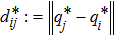
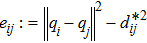
The gradient-based method is widely used to achieve the desired formation Eq*. One can construct a local potential function Vi for agent i:
Consider that the MAS consists of n double-integrator modeled agents and an additional agent labeled n + 1, which acts as the collective objective or the unique leader of the team. For ease of development, let the first n agents indexed by 1,2, . . ., n be the followers and the agent indexed by n + 1 be the team leader. The motion of follower i is given by
Denote by 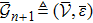
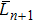
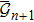


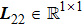
Let p* ∈ ℝdn be given and define the desired formation Eq*,p* for followers (
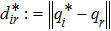
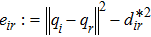
1) Inter-follower positions: 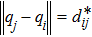
2) Follower-to-leader positions: 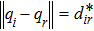
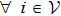
Let
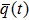
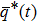
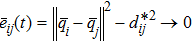
In this paper, the control objective for a group of double-integrator modeled agents is to achieve a formation that satisfies a given set of desired distance constraints and moving with the leader. Before starting the main problem, we list the assumption as follows.
We employ the gradient control laws and construct distance potential functions for stabilizing rigid formation shapes. To achieve the tracking control target, the control input for follower 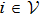
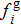
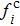
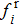
i) The gradient-based control term can be constructed as
ii) For each agent, the velocity consensus equation, defining how the neighbor of each agent influences and changes its velocity, is
iii) The tracking term 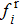
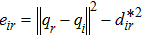
To facilitate the subsequent analysis, we use the following artificial potential function to show the sum of energy of all agents and the leader:
Let the following vector Φ be the gradients of potential functions of edges

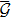

Then, the MAS model combining the controller (
The system (
Let qij = qi − qj and xij = xi − xj. The relative positions and velocities remain the same in the moving frame, i.e., xij = qij, vj − vi = pj − pi. Thus, eij(qij) = eij(xij) and 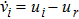
Using the control protocol (
The system is converted to a matrix form:
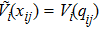
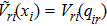
Let
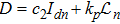
Before presenting the result on the stability analysis of distance-based formation behavior under control algorithm (
(I) All agents asymptotically move with the same velocity.
(II) Almost all solutions of system (
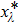
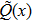
It should also be mentioned that if the agents are initialized on a collinear configuration in two-dimensional (2D) space, or on a coplanar configuration in 3D space, then they remain collinear or coplanar. These realizations and the flip vision are described as degenerate equilibrium in Ref. [11]. These extra equilibria are not expected. In this paper, since we focused on the local convergence of a gradient-based system, it is feasible to avoid the degenerate equilibrium by assuming that the initial formation is closer to the target formation than the degenerate equilibrium.
In the following, we concentrate on the analysis of asymptotic stability of the set Ω1. In this section, we first briefly introduce some basic concepts in center manifold theory that could be used to determine the stability of a nonlinear system when linearizing an equilibrium point. More details are available in Ref. [28]. We then consider the corresponding stability analysis using the center manifold theory.
Consider a system in normal form

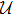
It can be shown that a center manifold always exists and the dynamic (
The stability of the system (
The set of correct equilibrium points can be written as
The advantage of using 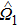
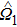
Consider Eq. (
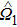
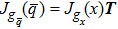

Next, it can be shown that JF(x, v) in Eq. (
We are now in a position to give the main result.
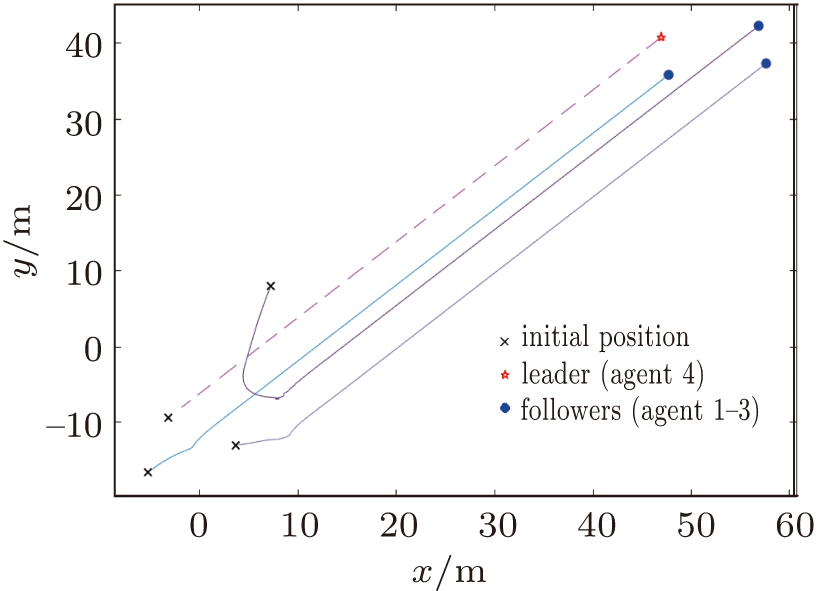
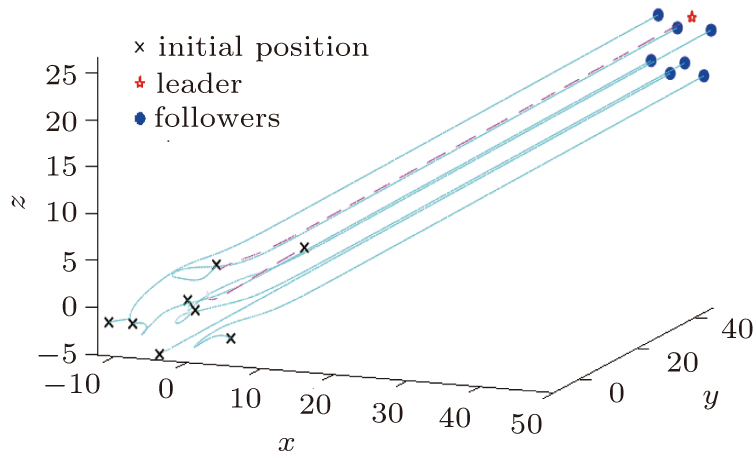
In this section, two illustrative examples are provided to verify the effectiveness of the proposed distance-based formation tracking control method for four double-integrator agents in two-dimensional (2D) space and eight double-integrator agents in three-dimensional (3D) space, respectively. The local convergence of the formation system with the tracking controllers is demonstrated.
Figures
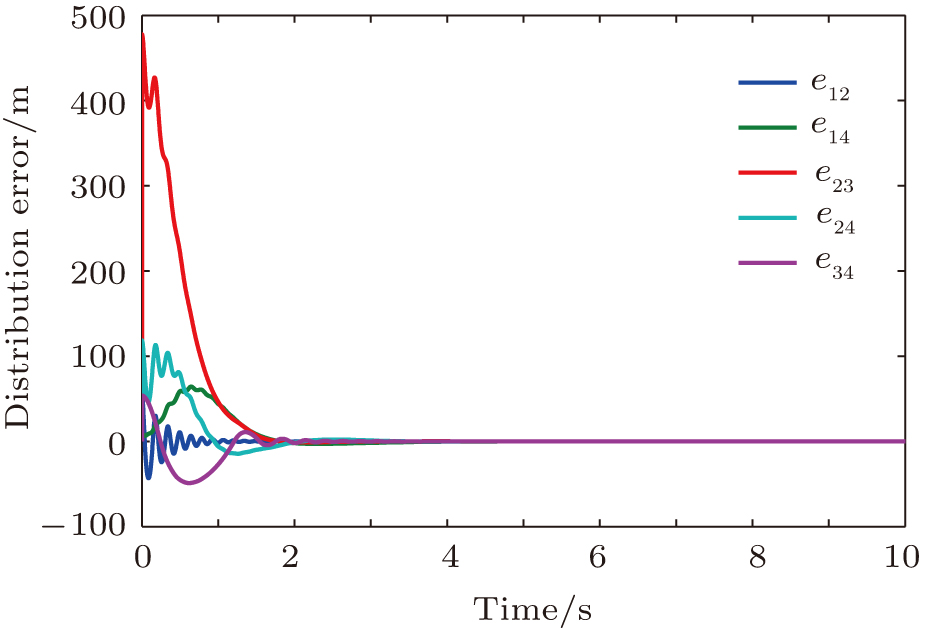 | Fig. 2. (color online) Asymptotic convergence of the distance errors for 2D rectangular formation tracking control. |
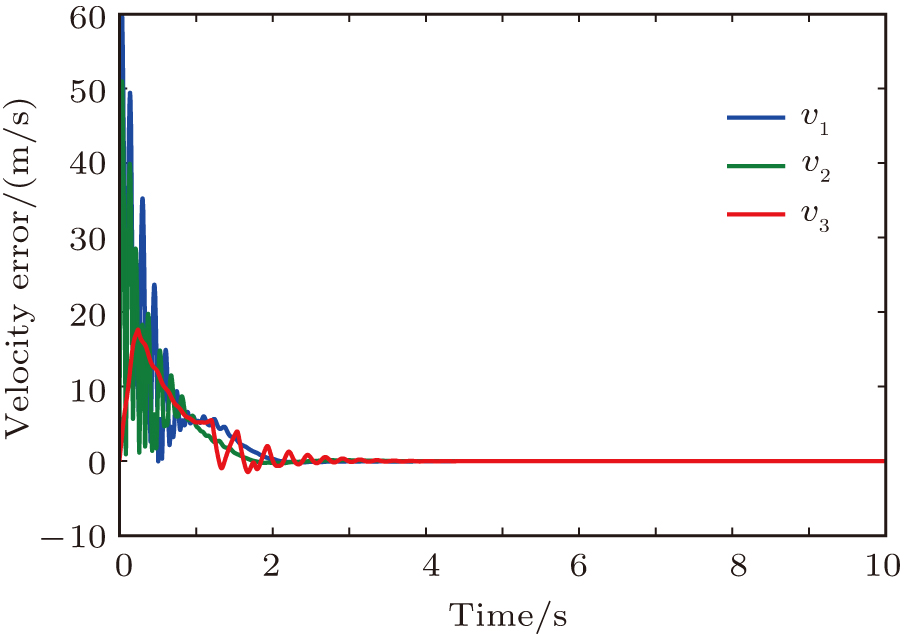 | Fig. 3. (color online) Asymptotic convergence of the velocity errors for 2D rectangular formation tracking control. |
| Table 2.
Selection for each edge of the corresponding potential function ρij. . |
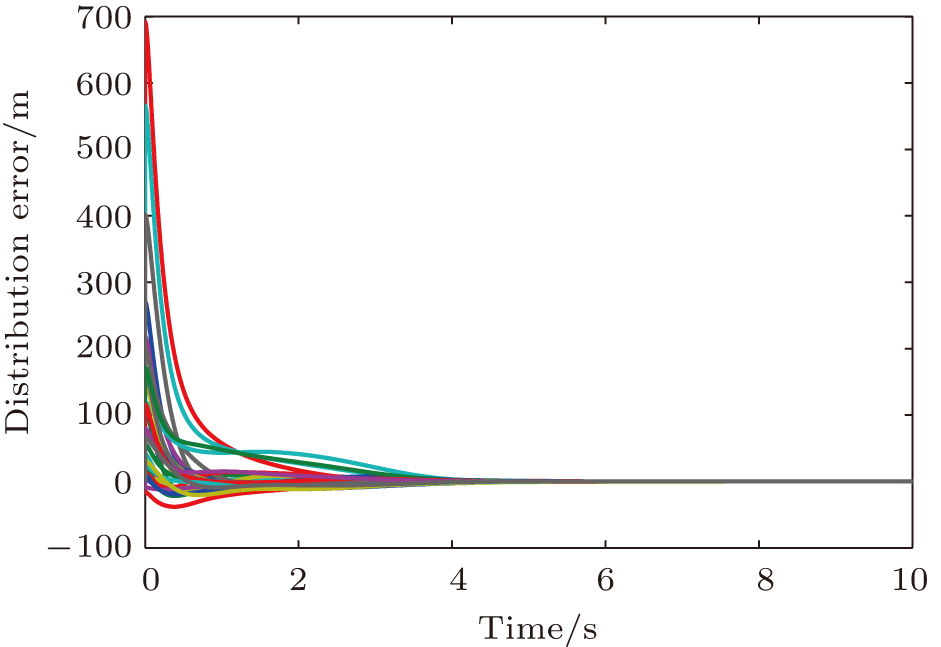 | Fig. 5. (color online) Asymptotic convergence of the distance errors for 3D cube formation tracking control. |
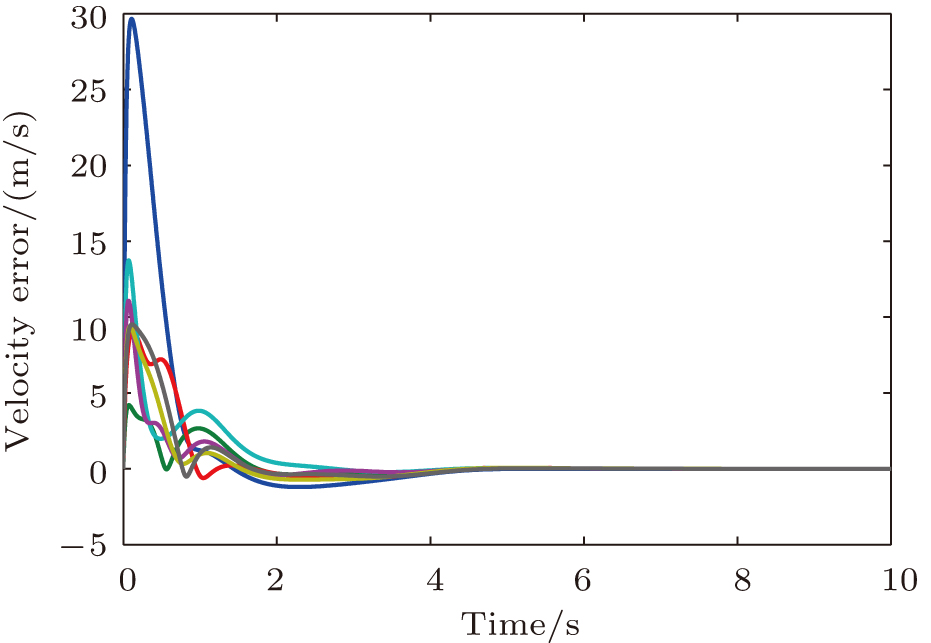 | Fig. 6. (color online) Asymptotic convergence of the velocity errors for 3D cube formation tracking control. |
We have investigated the distance-based formation tracking control for a group of double-integrator modeled agents. It is assumed that the state of the leader is time-varying and all agents with the leader communicate with each other according to an undirected fixed topology. With the target formation defined by inter-agent distances, the formation tracking controller is developed. The proposed controller can be decomposed to three terms, where the gradient-based term with potential function exhibited the formation target. Next, the asymptotic stability of the system with the proposed control law has been demonstrated. Two examples of the 2D plane and 3D space are provided to illustrate the validity of the theoretical results. The research on time-varying graphs and global stability analysis is ongoing.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |