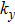† Corresponding author. E-mail:
Dirac semimetals are materials in which the conduction and the valence bands have robust crossing points protected by topology or symmetry. Recently, a new type of Dirac semimetals, so called the Dirac line-node semimetals (DLNSs), have attracted a lot of attention, as they host robust Dirac points along the one-dimensional (1D) lines in the Brillouin zone (BZ). In this work, using angle-resolved photoemission spectroscopy (ARPES) and first-principles calculations, we systematically investigated the electronic structures of non-symmorphic ZrSiS crystal where we clearly distinguished the surface states from the bulk states. The photon-energy-dependent measurements further prove the existence of Dirac line node along the X–R direction. Remarkably, by in situ surface potassium doping, we clearly observed the different evolutions of the bulk and surface electronic states while proving the robustness of the Dirac line node. Our studies not only reveal the complete electronic structures of ZrSiS, but also demonstrate the method manipulating the electronic structure of the compound.
Recently, a new type of quantum materials, so called Dirac semimetals (DSs), were discovered and intensively investigated for their rich physics and broad application potentials.[1–8] Different from regular insulators or metals, DSs are systems that host Dirac points (DPs, robust degeneracy points between conduction and valence bands) and Dirac fermions in their electronic structure and possess intriguing electronic transport behaviors such as high bulk carrier mobility and extremely large magnetoresistance.[4,5,9,10] The robustness of the Dirac points is usually protected by the crystal inversion or time reversal symmetry (e.g., in two-dimensional DS graphene[11] and three-dimensional DS Na3Bi[2,4] and Cd3As2[3,5–8]). Breaking the symmetry in DS would induce a topological phase transition and achieve other nontrivial phases. For example, three-dimensional (3D) Weyl semimetal[12–16] can be realized by breaking either time reversal symmetry or inversion symmetry in 3D DS.
More recently, a new type of DSs named Dirac line-node semimetals (DLNSs) were predicted in crystals with non-symmorphic symmetry (such as glide planes or screw axis). Unlike the previously studied DSs which contain discrete DPs, the additional symmetry in DLNSs induces and protects a band degeneracy at the Brillouin zone boundary, leading to one-dimensional (1D) Dirac line nodes.[17] The degeneracy at the line node is robust against perturbations (such as spin-orbit coupling effect (SOC)). Moreover, the DLNS is predicted to host unusual electric transport properties since 1D Dirac line-nodes are a more significant feature in the band structure and can have stronger contributions to the physically observable properties of the material (e.g., in electric transport).[18–21]
The line nodes have been predicted in various compounds, including the non-symmorphic compound ZrSiS and its isostructural family WHM (W = Zr, Hf, or La; H = Si, Ge, Sn, or Sb; M = O, S, Se or Te).[22] Previous band structure measurements on ZrSiS[19,23,24] and the related compounds ZrSiTe[25] and HfSiS[26,27] by angle-resolved photoemission spectroscopy (ARPES) have found signatures of the Dirac line-nodes and the surface states. However, since the previous measurements were taken with a few discrete photon energies, a more convincing identification of the bulk and surface states and detailed measurement on the line nodes are required. Furthermore, to better investigate the transport properties originated from the Dirac line-nodes, it would be desirable to manipulate the bulk and surface electronic states including the line-node structure in ZrSiS. All of these become the goals of our work.
In this work, we systematically studied the electronic structure of ZrSiS using high-resolution ARPES with broadly tunable photon energies. The measurement across multiple BZs identified a complete set of electronic structure, including the bands coming from both the bulk and surface electronic states. Especially, we identified the Dirac line node along the X–R direction, which proves the DLNS property in ZrSiS. Moreover, by surface potassium doping, we clearly observed the different evolution behaviors of the surface and bulk bands. We further noticed that the Dirac line node remains intact after the surface doping, proving the robustness from the symmetry protection. Our finding provides detailed information on the electronic structure of ZrSiS and proposes a method for manipulating its electronic structure for future investigations and applications.
Single crystals of ZrSiS were grown by a chemical vapor (iodine (I2) as a transport agent) transport method in a two-step process. First, the polycrystalline ZrSiS powders were synthesized by direct solid-state reaction using high-purity elementals Zr, Si, and S in cleaned quartz ampoules. The stoichiometric amounts of ternary mixture were heated to 1100 °C and maintained at this temperature for 7 days to make the reaction complete. Then, we could obtain the single phase products after the samples were quenched to room temperature. Second, the as-prepared polycrystalline ZrSiS powder together with I2 was sealed in a quartz tube. Then the quartz tube was kept in a two-zone furnace for 10 days with the growing temperature profile of 1150–1000 °C. The metallic luster crystals were obtained for ARPES measurements.[20]
The ARPES experiments were performed at the beamline I05 of the Diamond Light Source (DLS), beamline 10.0.1 of the Advanced Light Source (ALS) and beamline 13U of the National Synchrotron Radiation Laboratory (NSRL), Hefei, China, all of them were equipped with Scienta R4000 analyzers. The measurement sample temperature and pressure were 10 K (20 K in ALS) and lower than 
The band structure and Fermi surface of bulk and slab ZrSiS were calculated by the OpenMX code[28] within the framework of the density functional theory in the generalized gradient approximation.[29] The bases are s3p2d2, s2p2d1, and s3p3d2f1 for Zr, Si, and S elements, respectively. The energy cutoff for real-space integration is 250 Ry.
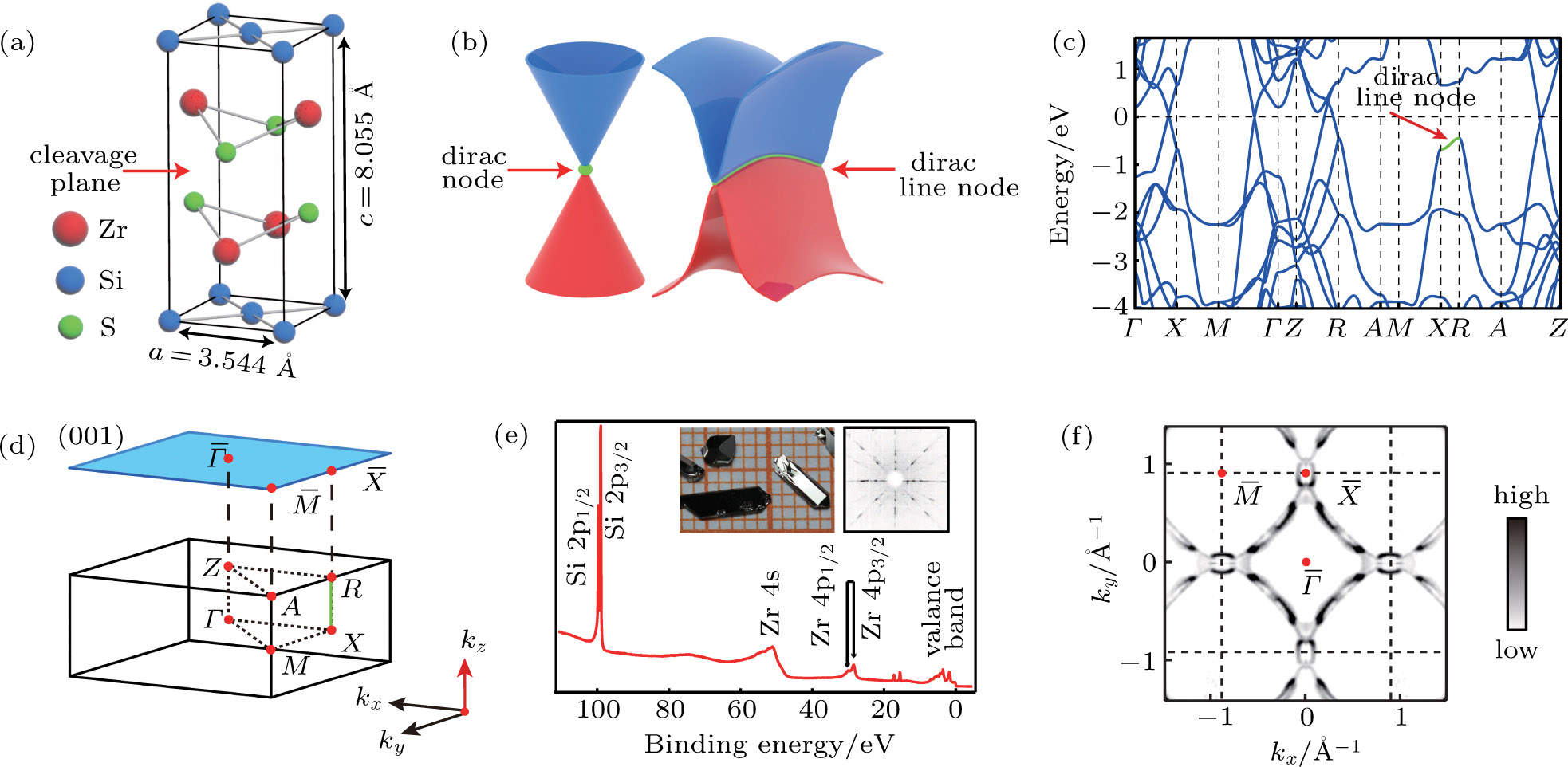
The crystal structure of ZrSiS is shown in Fig. 
After cleaving, large flat and shiny surfaces are exposed, which are ideal for ARPES measurements. The high quality of the crystal can also be verified by the Laue patterns and the core level photoemission spectrum which clearly shows the characteristic Zr4s, Zr4p, and Si2p peaks (Fig.
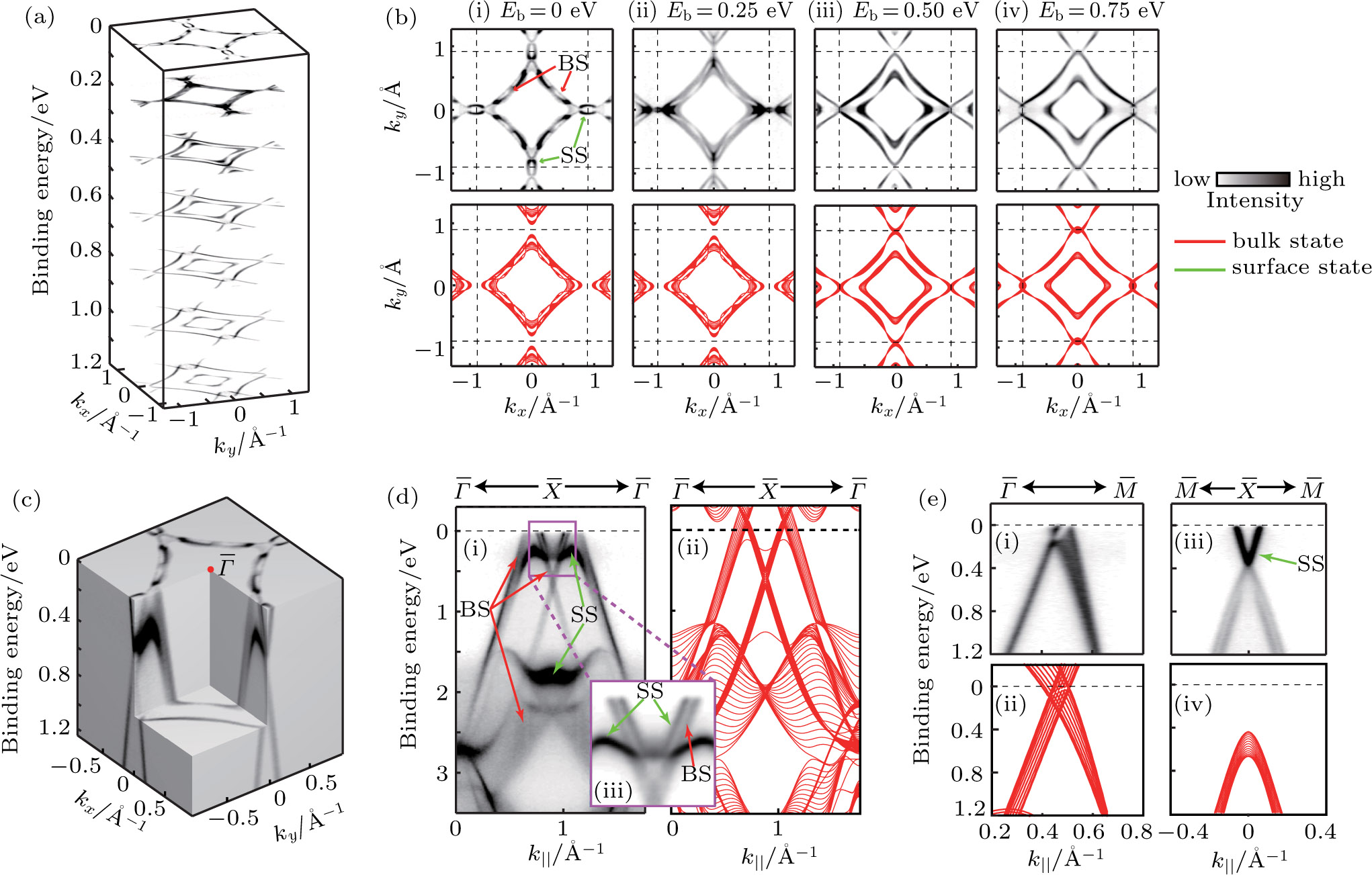
To investigate the detailed electronic structure of ZrSiS, we focus on the first BZ by carrying out high-resolution ARPES measurements, and the results are shown in Fig. 


In addition to the constant energy contours, we focus on the dispersions along the high symmetry directions (Figs. 

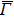
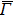








The surface and bulk nature of the electronic bands are further supported by the photon-energy-dependent measurement which probes the band dispersion at different kz values. By a series of measurements at different photon energies, we clearly identify the surface and bulk bands in the FS at 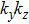


Finally, we demonstrate the modification of the electronic structure of ZrSiS by introducing alkaline metal onto the sample surface. The stacking plots of constant-energy contours (Fig. 

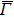
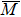
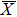


In summary, our systematic measurement of the electronic structure of the ZrSiS compound has obtained the full set of band structure in the BZ, including the electronic states originated from both the bulk and surface. Our measurement of the Dirac line node convincingly establishes that ZrSiS is a DLNS protected by non-symmorphic symmetry. Our in-situ K-doping data illustrates the different behaviors of the surface and bulk bands, as well as the robustness of the Dirac line-node. These band characteristics not only help us understand the intriguing transport properties in ZrSiS, but also point to methods in manipulating the electronic properties in DLNS.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |