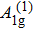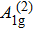† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51771126 and 11774247), the Youth Foundation of Science and Technology Department of Sichuan Province, China (Grant No. 2016JQ0051), and the World First-Class University Construction Funding.
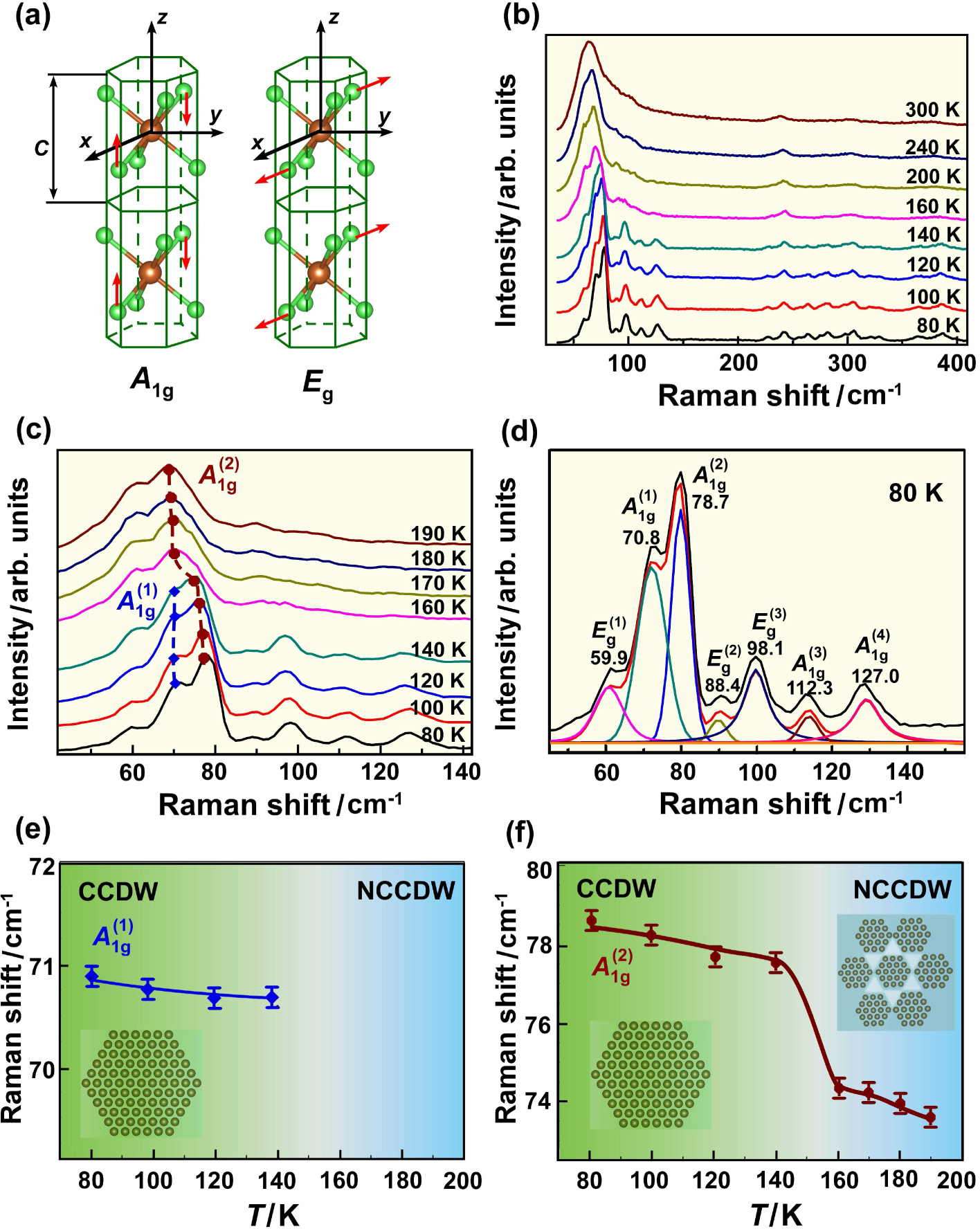
The evolution of electron correlation and charge density wave (CDW) in 1T-TaS2 single crystal has been investigated by temperature-dependent Raman scattering, which undergoes two obvious peaks of A1g modes about 70.8 cm−1 and 78.7 cm−1 at 80 K, respectively. The former peak at 70.8 cm−1 is accordant with the lower Hubbard band, resulting in the electron-correlation-driven Mott transition. Strikingly, the latter peak at 78.7 cm−1 shifts toward low energy with increasing the temperature, demonstrating the occurrence of nearly commensurate CDW phase (melted Mott phase). In this case, phonon transmission could be strongly coupled to commensurate CDW lattice via Coulomb interaction, which likely induces appearance of hexagonal domains suspended in an interdomain phase, composing the melted Mott phase characterized by a shallow electron pocket. Combining electronic structure, atomic structure, transport properties with Raman scattering, these findings provide a novel dimension in understanding the relationship between electronic correlation, charge order, and phonon dynamics.
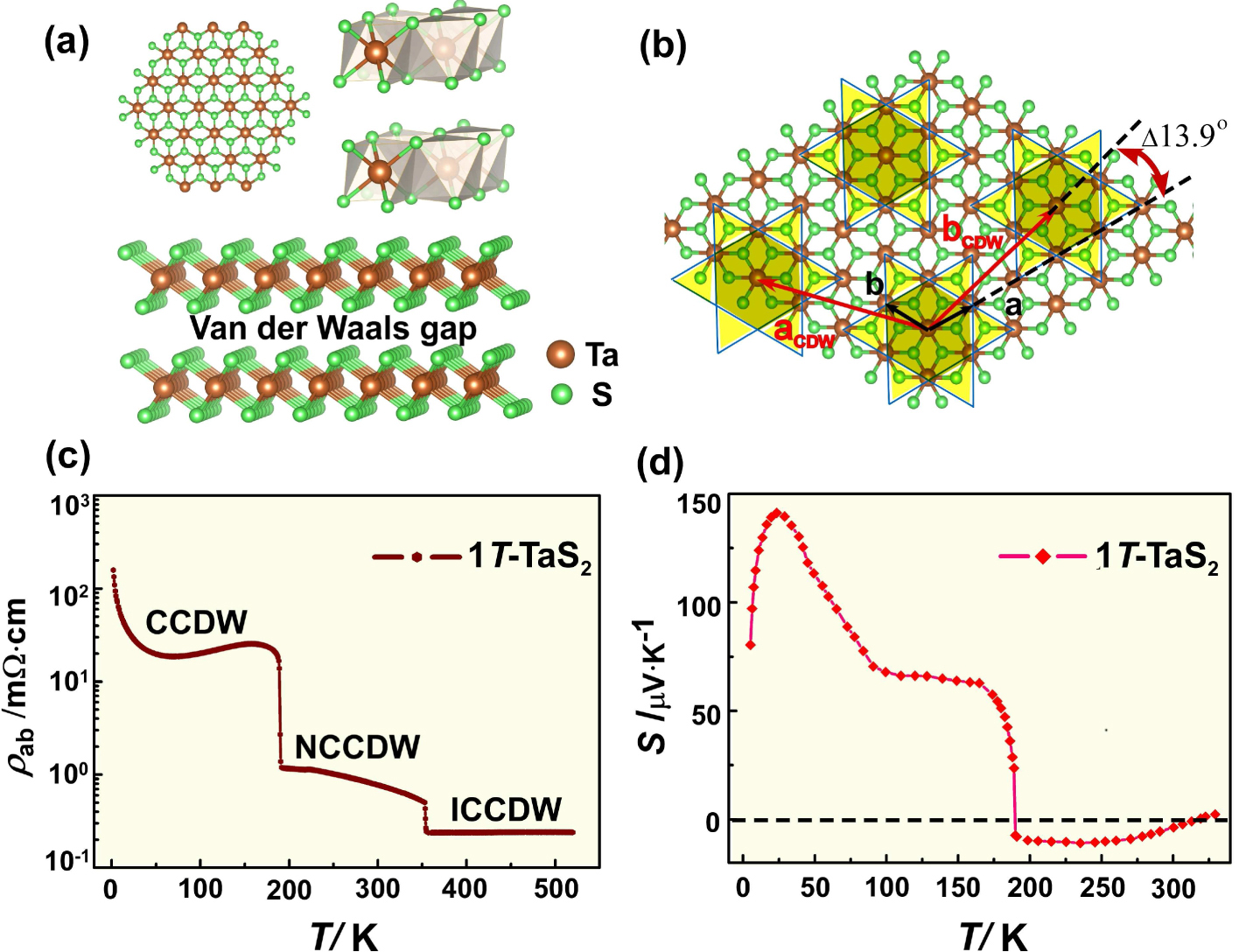
Coexistence, competition, and collaboration of electron correlation with charge order or charge-density-wave (CDW) are a long-term unresolved issue in low dimensional physics. While the CDW order is well understood by the conventional Peierls mechanism in terms of Fermi-surface nesting due to electron–phonon coupling, electron correlation also plays a crucial role as well in some circumstances.[1–4] Layered transition-metal dichalcogenides (TMDs)[5–8] provide an ideal platform for investigating the interplay in that their intrinsic two-dimensional structure is susceptible to electronic instability. Among many TMDs, it has attracted much attention in 1T-TaS2, where its CDW phases include nearly commensurate CDW (NCCDW) and commensurate CDW (CCDW) phases. Additionally, its CCDW phase is compatible to the Mott insulating phase because of the strong electron–phonon and electron–electron interactions.[9–13]
Current explanation of 1T-TaS2 and its associated phases, which is focused mainly on electronic states, can be summarized in four aspects: (i) Ta atoms are displaced to form star-of-David clusters where 12 Ta atoms contract toward a central Ta atom, interlocking each cluster to form a triangular superlattice.[9,10,14] However, the 12 electrons dominate the states below the distortion-induced gap and the thirteenth one occupies the states above the gap, leading to a Mott insulating state which is responsible for high resistivity of the CCDW phase.[15–17] (ii) The neighbouring NCCDW phase contains the star-of-David clusters, although they are less uniformly arranged.[9] (iii) Upon increasing temperature, the Mott phase melts into the NCCDW phase (the melted Mott phase) with an extremely fast charge response and a sudden resistivity drop, where several tens of stars organize into roughly hexagonal domains.[12,18] These reproduce locally the CCDW Mott phase, revealing that the CCDW mechanism is beyond the framework of the conventional Peierls picture.[19–22] (iv) The CCDW superlattice structure could be described by the trigonal structure due to the weak interlayer interaction.[23,24] Definitely, none of them have verified a seemly counter-intuitive origin in understanding the low-dimensional electron system.
In this work, we provide definitive evidence that electron-correlation-driven Mott transition and NCCDW transition (melted Mott transition) can be directly confirmed by Raman scattering in 1T-TaS2. The observed melted Mott phase reflected by a shallow electron pocket, i.e., likely hexagonal domains which pinned in an interdomain phase, could originate from strong coupling between phonon excitation and CCDW lattice. Combining the microstructure, transport properties, electronic structure with Raman scattering, the findings presented here may provide insight into approaches for manipulating various CDW phases to understand underlying physics in low-dimensional electron systems.
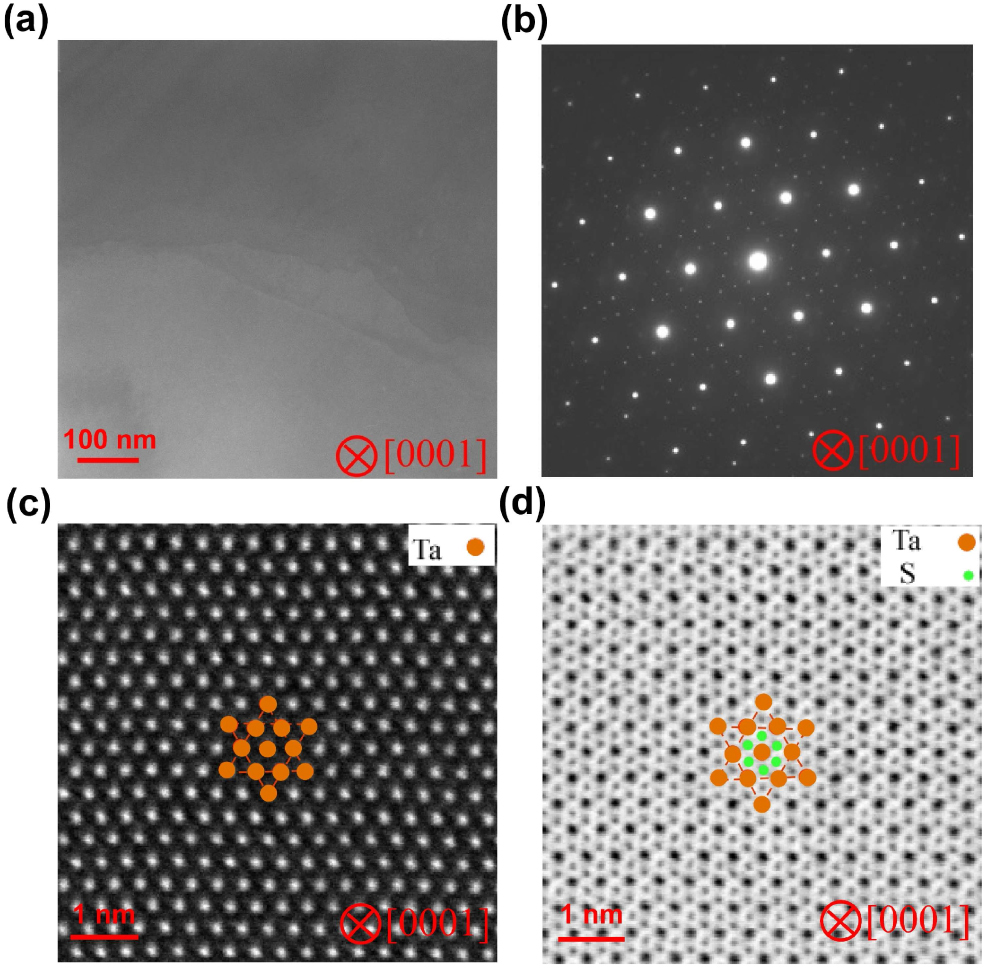
High-quality single crystals of 1T-TaS2 was grown by the chemical vapor transport technique with iodine as a transport agent. The temperature dependence of resistivity and Seebeck coefficient were carried out using a standard four-probe configuration in a quantum design physical properties measurement system (PPMS). Thin-foil specimens for transmission electron microscopy (TEM) and scanning TEM (STEM) imaging were prepared by cutting single crystal from [0001] (c axis). The selected-area diffraction pattern (SADP) and TEM images were taken using the JEOL JEM-2010 F electron microscope operated at 200 kV. The high-angle annular dark-field (HAADF) and annular bright-field (ABF) images were taken with a 200-kV ARM-200FC STEM equipped with a probe corrector (CEOS Gmbh). Raman scattering spectra were recorded through a custom-built Raman system using a triple grating monochromator (Andor Shamrock SR-303i-B, EU) with an attached electron-multiplying CCD (ANDOR Newton DU970P-U VB, EU) excited with a 532 nm solid-state laser (RGB laser system, Germany). Low-temperature Raman experiments were performed with the Freezing Stage (THMS600, UK). Angle-resolved photoemission spectroscopy (ARPES) measurements were performed using a VG-SCIENTA SES2002 spectrometer with a high-flux He discharge lamp. The He–Iα (hν = 21.218 eV) resonance line was used to excite photoelectrons.
Figure 
To examine the microstructure of 1T-TaS2, we performed TEM and SADP observed from [0001] orientation as shown in Figs. 
To track the dynamical properties of lattice vibrations, we carried out Raman scattering measurements. There are two Raman-active phonon modes including A1g and Eg modes,[27–29] in which A1g mode refers to two S atoms per unit cell move relative to one another along z orientation, while a doubly-degenerate Eg mode reflects S atoms move opposite to one another along x or y orientation, as plotted in the inset of Fig. 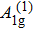
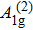
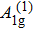
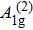
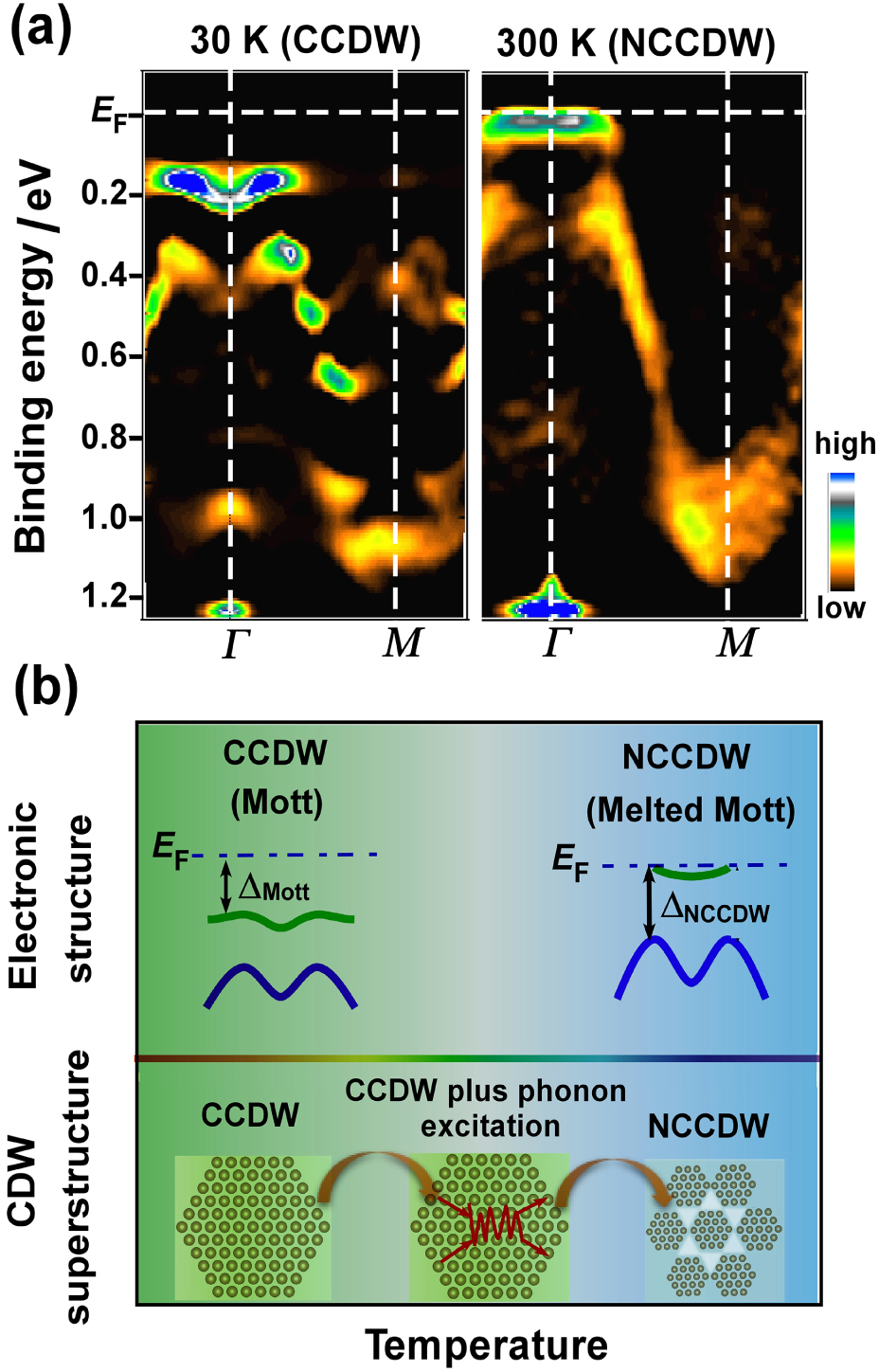
To gain more insights into correlation between CCDW (Mott phase), NCCDW (melted Mott phase), electronic structure, and phonon transmission, we performed band dispersions based on ARPES along the ΓM cut measured at 30 K (Mott phase) and 300 K (melted Mott phase) as shown in Fig. 
Figure
We have reported the temperature dependence of Raman scattering in layered 1T-TaS2 single crystal. We found direct evidence for electron-correlation-driven Mott transition and NCCDW transition (melted Mott transition) derived from Raman scattering. The electronic structure demonstrates that the shallow electron pocket is responsible for the melted Mott phase, where the possible hexagonal domains pinned in the interdomain phase, revealing strong coupling between phonon excitation and CCDW lattice. The present results not only render to recognize the intrinsic origin of Mott and NCCDW phases, but also provide a deep insight into close association between electronic correlation, charge-order state, and dynamical motions of phonons.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |