† Corresponding author. E-mail:
Project supported by the National Key Research Development Program of China (Grant No. 2016YFB0701204) and the National Natural Science Foundation of China (Grant Nos. U1302272 and 51571055).
A phase-field model is modified to investigate the grain growth and texture evolution in AZ31 magnesium alloy during stressing at elevated temperatures. The order parameters are defined to represent a physical variable of grain orientation in terms of three angles in spatial coordinates so that the grain volume of different order parameters can be used to indicate the texture of the alloy. The stiffness tensors for different grains are different because of elastic anisotropy of the magnesium lattice. The tensor is defined by transforming the standard stiffness tensor according to the angle between the (0001) plane of a grain and the direction of applied stress. Therefore, different grains contribute to different amounts of work under applied stress. The simulation results are well-explained by using the limited experimental data available, and the texture results are in good agreement with the experimental observations. The simulation results reveal that the applied stress strongly influences AZ31 alloy grain growth and that the grain-growth rate increases with the applied stress increasing, particularly when the stress is less than 400 MPa. A parameter (Δd) is introduced to characterize the degree of grain-size variation due to abnormal grain growth; the Δd increases with applied stress increasing and becomes considerably large only when the stress is greater than 800 MPa. Moreover, the applied stress also results in an intensive texture of the ⟨0001⟩ axis parallel to the direction of compressive stress in AZ31 alloy after growing at elevated temperatures, only when the applied stress is greater than 500 MPa.
Magnesium alloys, the lightest metallic structural materials, have attracted significant attention in automotive and aerospace industries. However, because of the presence of limited slip systems stemming from their hexagonal close-packed structures, magnesium alloys exhibit relatively low strength and poor plasticity at room temperature; these shortcomings restrict their range of applications as engineering materials.[1–3] One of the most effective methods to improve their properties is to modify their microstructures, such as grain sizes, morphologies, or textures.[4–6]
Crystallographic texture is known as a main source of polycrystalline material plastic strain anisotropy and influences most of the mechanical, physical, and chemical properties of polycrystalline materials.[7–13] In the case of AZ31 magnesium alloy, the hot-rolled AZ31 magnesium alloy exhibits a strong basal texture with the 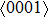

The phase-field method is a physical and mathematical model used to predict microstructure evolution phenomena and offers unique advantages in studying the effect of applied stress on the microstructural evolution of alloy.[16] For instance, Wen et al.[17] used the phase-field method to investigate the effect of an applied homogeneous strain on the coherent α2 to O-phase transformation in Ti–Al–Nb alloys. Guo et al.[18] used the phase-field model to study the effect of a superimposed stress on the coarsening of interacting Ni4Ti3 particles. Recently, several researchers have studied the effect of strain on texture evolution by using the phase-field method. Kim et al.[19] established a phase-field model combined with a micro-elasticity effect including elastic anisotropy and inhomogeneity to investigate the effects of micro-elasticity on grain growth and texture evolution in polycrystalline thin film with columnar grain structure. Darvishi Kamachali et al.[20] proposed a phase-field model that used the contribution of stored mechanical energy to investigate texture evolution in deformed AZ31 magnesium alloy sheets. Bahattacharyya et al.[21] developed the phase-field method integrated with a crystal plasticity effect to investigate the stress-driven grain-boundary migration in elastically inhomogeneous polycrystalline materials. Lu et al.[22] used the phase field method to study the effect of the second phase particle on texture evolution of polycrystalline material based on Bahattacharyya’s work. However, the studies of influences of elastic strain energy on texture evolution and grain growth by the phase-field method are not found in the literature probably because it is generally believed that texture and grain growth at high temperature are determined by anisotropic plastic strain in terms of stored energy only, and features of elastic strain energy have no effect.[12] The aim of this simulation is to prove the possibility that anisotropic elastic strain energy plays an important role in texture formation as well during grain growth under applied stress. This model works on the assumption that the stored energy is immediately released in the case that AZ31 alloy is deformed slowly with temperature increasing. Our previous work already established a phase-field model which takes the contribution of stored energy into consideration to simulate the grain growth process of AZ31 alloy in real time and space by introducing a novel concept of the grain boundary range.[23–26]
In this study, we develop a phase-field model to investigate the influences of elastic strain energy on grain growth and texture by setting no plastic strains in AZ31 Mg alloy. The order parameters are defined to represent a physical variable of grain orientation so that elastic energy and texture can be expressed by analytical formulas. The anisotropic elastic energy in grain as an extra grain growth driving force is calculated in the present work under applied stress and is different among grains due to different angles of grain orientation with respect to the applied stress direction. The simulation results are explained by using the experimental data. This work will provide a new general theoretical guideline for developing the industrial magnesium alloys.
Phase-field methods are based on classical thermodynamics and kinetics theory. The phase-field model uses a set of field variables (e.g., concentration field variable and order parameters) to simulate complex microstructures. The temporal evolution of the microstructure can be determined by solving the time-dependent Ginzburg–Landau equation[27] and the Cahn–Hilliard diffusion equation[28] as follows:

The free energy of the system F is expressed as a function of the chemical free energy Fch and the elastic free energy Eel as follows:
The concentration field variable is dependent on the order parameter at any position; i.e., the gradient form of concentration is a function of the gradient form of the order parameter. It is equivalent to choose any of the gradient forms as zero and we choose the concentration to be zero as in previous work.[29] Therefore, the single-phase system chemical free energy is typically expressed as
In the present study, based on the work of Wu et al.[25] and He et al.,[26] the following expression is introduced to describe the free energy density function:
On the basis of the linear elasticity theory introduced by Khachaturyan,[30] the elastic energy of a homogeneous anisotropic system can be expressed as a function of ηp(r, t) as follows:

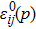
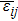
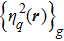

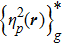

In this model, the same stress is applied to all grains, but the strain is different according to the different orientation of grains. The elastic inhomogeneity could result in different eigenstrains for different grains according to the linear elasticity theory proposed by Khachaturyan.[30] Therefore, the eigenstrain is coupled to generate elastic energy by the 3rd term as well as a relaxation that affects each other in the 4th term. Actually, it can be traced back to Eshelby’s classical work on transformation-induced elasticity,[31] this strain comes from the mismatch strain. The eigenstrain tensor of each orientation is obtained by transforming the constant tensor with respect to the crystal coordinate system of 
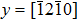

Each orientation is represented by the three Euler angles φ1, Φ, and φ2, and each order parameter η p(r, t) is defined to represent a physical variable of the grain orientation as shown in Table
| Table 1.
Corresponding relationship between order Parameters and Euler angles. . |
This simulation investigates the elastic strain energy effect via a mock situation where the AZ31 alloy is deformed slowly at an elevated temperature that was sufficiently high to immediately relieve the stored energy in dislocation annihilation by means of dislocation climbing. Therefore, it is believed that plastic strain has a minor effect in this particular case.[33] The parameters related to the chemical free energy in Eqs. (
| Table 2.
Values of model parameters at different temperatures. . |
The simulations are performed in a two-dimensional (2D) grid size of 10242 cells. A three-dimensional (3D) simulation is also carried out for comparison with the 2D simulation; the 3D size is 5123 grid cells. Each grid cell is 0.1 μm in size and the time step value is selected as 0.2 s in this model to maintain a balance between convergence and efficiency. The periodic boundary condition is imposed. The initial microstructure is defined as an average grain size of 11 μm with grains being in randomly different crystallographic orientations. The initial Al concentration is set to be a different value according to the local initial η value. If η = 1, the local initial concentration is set to be 0.03, and at other positions it is set to be 0.031 for simulating the element boundary segregation. This simulation uses the semi-implicit Fourier-spectral method to solve the model Eqs. (
The simulation is performed in both 2D and 3D cases to investigate the effects of an applied stress of 400-MPa on the grain growth in polycrystalline AZ31 Mg alloy. In the case of the 2D simulation, the microstructure after the alloy has been annealed at 673 K for 60 min is shown in Fig.
A comparison between the 2D and 3D simulation results in Fig.
In this study, we investigate the effects of different applied stress values on the grain growth in polycrystalline AZ31 alloy. The direction of stress is crucial, indeed if local behavior and morphology are chiefly concerned. However, the direction of stress is isotropic in an enormous system of randomly oriented grains. We arbitrarily choose a stress direction parallel to the z axis for convenience. The evolutions of the microstructures during grain growth under different applied compressive stresses are plotted in Fig.
In order to quantitatively investigate the variation of average grain size, we simulate the variations of grain size with annealing time under different applied stresses. Figure
 | Fig. 4. (color online) Plots of average grain size of AZ31 magnesium alloy as a function of annealing time under different applied stresses at 673 K, determined by simulation. |
The distributions of grain size in AZ31 alloy annealed for 100 min under several different applied stresses are shown in Fig.
To obtain an accurate expression for grain-size variation, we introduce a parameter Δd to describe it: Δd = dmax − dmin, where dmax represents the maximal characteristic grain size, which is the average size of the 10% of the largest grains in a system, and dmin is the minimal characteristic grain size, which is the average size of the 10% of the smallest grains. The simulated grain-size variations with processing time are plotted in Fig.
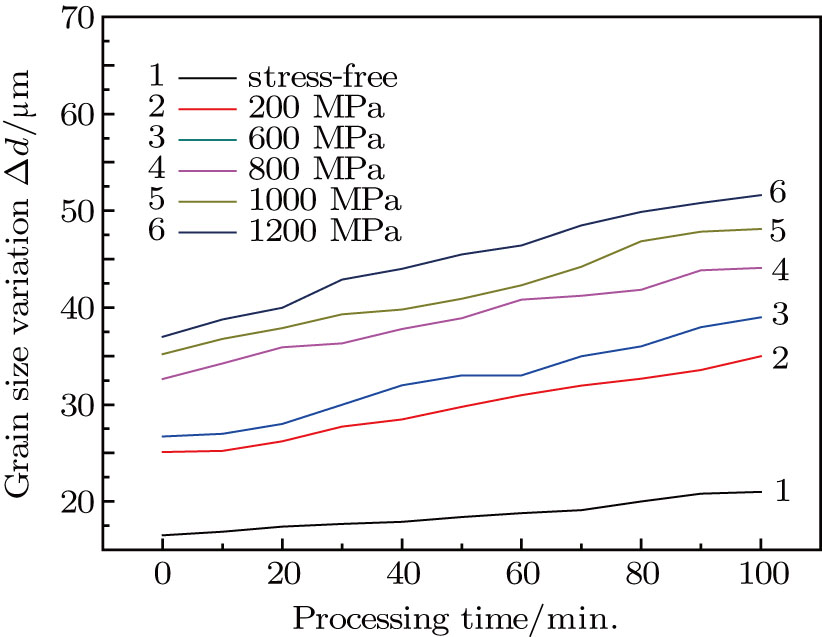 | Fig. 6. Plots of simulated grain size variation (Δd) as a function of the annealing time for growth at 673 K under different applied stresses. |
In this work, we simulate grain growth under applied stress on an industrial application scale. It is necessary to explore the significance of applied stress in industrial applications. Figure
 | Fig. 7. Simulated grain growth in AZ31 alloy with and without applied stress for comparison with experiments at 623 K:[37,38] curves 1, 2, and 3 are simulations at a nucleation rate of 0.010, obtained by our model setup, and the growth rates are different obtained by fitting the simulation data to Eq. ( |
Figure 
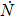


| Table 3.
Values of k at different growth times in Eq. ( |
The AZ31 specimen of our simulation is compressed at 673 K. The direction of compressive stress is along the z axis in space coordinate. In the simulation, texture evolution starts with the same initial random texture microstructure. Figure 

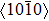
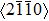
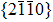
 | Fig. 8. Simulated texture of AZ31 alloy after being annealed at 673 K for 40 min and 100 min with and without applied stress: (a) and (b) stress-free, (c)–(d) under 600 MPa applied stress, and (e) EBSD experimental texture corresponding to AZ31 samples dynamically loaded at 523 K in compression along the normal direction to a strain of 0.17.[40] |
In order to better understand texture evolution, we quantitatively study the variation of the texture area. Figure 
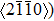
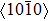
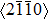
 | Fig. 9. Texture evolutions upon grain growth in AZ31 alloy with and without applied stress: (a) without applied stress and (b) 600 MPa applied stress. |
The topological structure is a particularly important characteristic in polycrystalline alloy, it will play a key role in grain-growth dynamics. Therefore, it is necessary to investigate the topological evolution of each individual grain during growth and shrinkage.
Note that von Neumann and Mullins gave a correlation between the growth rate of n-sided grain in two dimensions and the topological class of each individual grain under the stress-free condition:[41]
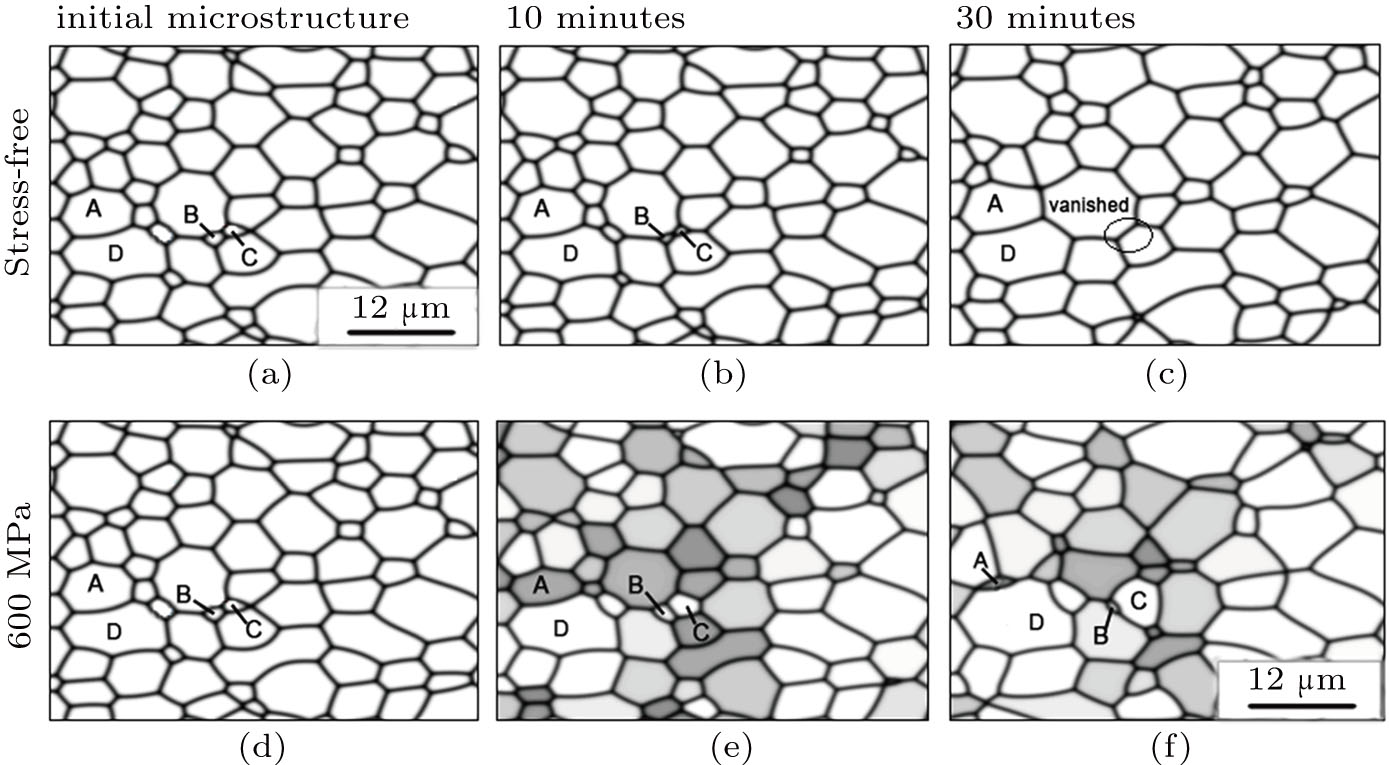 | Fig. 10. Topological evolutions of microstructure under (a)–(c) no stress and (d)–(f) 600 MPa applied stress to demonstrate some topological transformation features at 673K during annealing time. |
Figures
This phase-field model is established to simulate the effects of applied stress on grain growth and texture in polycrystalline AZ31 alloy. Moreover, this model is sufficiently flexible to be adapted to simulating other alloy systems under applied stress by changing the value of the dynamic parameters and the expression of f0.
(i) A phase-field model is modified to simulate grain growth and texture evolution in AZ31 magnesium alloy at elevated temperatures under an applied stress field by determining different stiffness tensors for each grain orientation with respect to the direction of applied stress. The texture results exhibit good agreement with the experimental observation.
(ii) Applied stress strongly influences grain growth in AZ31 alloy at elevated temperature, and the grain-growth rate increases with applied stress increasing, particularly when the applied stress is less than 400 MPa.
(iii) A parameter (Δd) is introduced to show the degree of grain size variation due to abnormal grain growth and the Δd increases with increasing applied stress. The Δd becomes severely large only when the stress is greater than 800 MPa.
(iv) Applied stress would result in an intensive texture of ⟨0001⟩ along the compressive stress direction in AZ31 alloy grown at elevated temperature only when the applied stress is greater than 500 MPa.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |





