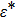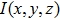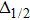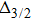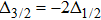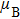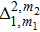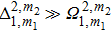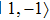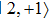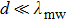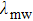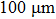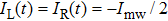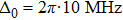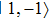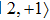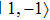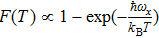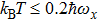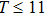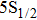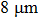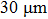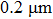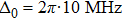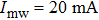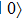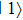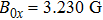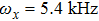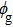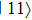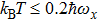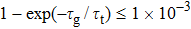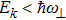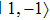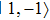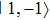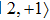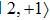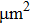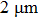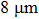Microwave coherent manipulation of cold atoms in optically induced fictitious magnetic traps on an atom chip
1. IntroductionIn the last 15 years, atom chips have proven to be appealing systems for trapping and manipulating ultracold atoms.[1] They provide not only long coherence time in isolated magnetic traps, but also versatile micropotentials in a robust, compact, and scalable set-up.[2] The key point for handling microscopic cold atoms with atom chips is to construct various forms of potentials using magnetic, electrostatic, optical, and plasmonic fields. This is realized by integrating current-carrying wires, permanent magnetic materials, electrodes, and micro-optic elements on microscale substrates. Impressive achievements have been already demonstrated, such as Bose–Einstein condensates (BEC) in magnetic traps,[3–5] matter-wave interferometry,[6] atomic clock,[7] coherent atomic control by radio frequency (RF)[8] and microwave (MW) potentials,[9] and integrated micro-optics[10–13] and micro-cavities[14] for atom–light interactions. With the development of integrating and miniaturizing technology, atom chips with enhanced accuracy and versatility are expected to enable applications from fundamental physics research to practical integrated devices.[1]
As atom chips combine so many important features, they are considered as promising candidates for implementing quantum information processing (QIP). Numerous physical systems for quantum computing in magnetic traps on atom chips have been proposed.[15–18] However, the experimental demonstration of two-qubit quantum gates operation on an atom chip is still a formidable task. There are some restrictions that limit the practical implementation of quantum gates operation in those proposals. On one hand, individually addressing a single qubit in a magnetic trap lattice on an atom chip is very difficult, because the magnetic field cannot be localized precisely, especially in a single atom magnetic microtrap. On the other hand, configuring the magnetic trap lattice needs complicated current-carry wires and uniform bias magnetic fields, which makes the chips difficult to fabricate and integrate.
In this study, we propose a new hybrid atom chip for quantum manipulation of cold atoms by combining for the first time optically induced fictitious magnetic field (OFMF) and MW state-dependent potentials, which could beat the limitations mentioned above. By taking advantage of the optically induced fictitious magnetic traps (OFMTs) and MW potentials, the resulting hybrid chip has important features compared with the existing schemes. (i) The OFMTs can be addressed directly along the laser beam propagation direction, which is very important for quantum internal states initialing, manipulating, and detecting. This would allow coherent manipulations to be scaled to a periodic array of atoms from the initially proposed two-qubit operations. (ii) The MW potentials can control the atoms’ external states precisely in the OFMTs since the laser beam can be focused close to the micrometer-sized microwave coplanar waveguides (CPWs), where much stronger MW gradients can be realized with only milliwatts of power[9] and the fictitious magnetic field works locally with strong confinement. Consider an MW waveguide in our chip carrying a microwave current of  , corresponding to a microwave signal of P = 10 mW, the microwave induces a field gradient
, corresponding to a microwave signal of P = 10 mW, the microwave induces a field gradient  at a distance of
at a distance of  , which varies on a micrometer scale and leads to strong potential gradients for state selective operations. (iii) An OFMT with an extremely small trapping volume can be achieved with a tightly focused laser beam, which possesses similar properties as a single atom optical dipole trap. For the previously proposed chip-based quantum gate schemes, the physical systems are realized based on making assumption of ideal stationary magnetic trap potentials with exactly only one atom loaded per well.[15,17] Here we derive an exact single atom trap potential with a photonic chip focused 790 nm laser beam (beam waist
, which varies on a micrometer scale and leads to strong potential gradients for state selective operations. (iii) An OFMT with an extremely small trapping volume can be achieved with a tightly focused laser beam, which possesses similar properties as a single atom optical dipole trap. For the previously proposed chip-based quantum gate schemes, the physical systems are realized based on making assumption of ideal stationary magnetic trap potentials with exactly only one atom loaded per well.[15,17] Here we derive an exact single atom trap potential with a photonic chip focused 790 nm laser beam (beam waist  , within the regime of collision blockade effect). The axial and transverse trap frequencies obtained with such OFMT are
, within the regime of collision blockade effect). The axial and transverse trap frequencies obtained with such OFMT are  and
and  , respectively, which are of the same orders of magnitude as the assumed ideal magnetic trap parameters. Pioneering techniques on manipulating both internal and external states of single atoms in optical dipole traps in free space[19–22] pave the way for developing such integrated on-chip single-atom quantum devices. (iv) The OFMF and MW fields can be controlled electronically in a fast and accurate way, allowing the potential parameters and the operation dynamics to be optimized. By applying optimal control of the MW field, a total operation infidelity of the order of only a few 10−3 could be reached with many system errors taken into account, which is already sufficient for scalable quantum computation. (v) Composing complex atomic potentials with laser beams and coplanar waveguides only requires a simpler on-chip platform design, because the laser beams replacing the uniform bias magnetic field lead to a more convenient and flexible experimental setup. Thus, the chip system could get rid of bulky Helmholtz coils and can be further integrated with tailored photonic waveguides.[12,13]
, respectively, which are of the same orders of magnitude as the assumed ideal magnetic trap parameters. Pioneering techniques on manipulating both internal and external states of single atoms in optical dipole traps in free space[19–22] pave the way for developing such integrated on-chip single-atom quantum devices. (iv) The OFMF and MW fields can be controlled electronically in a fast and accurate way, allowing the potential parameters and the operation dynamics to be optimized. By applying optimal control of the MW field, a total operation infidelity of the order of only a few 10−3 could be reached with many system errors taken into account, which is already sufficient for scalable quantum computation. (v) Composing complex atomic potentials with laser beams and coplanar waveguides only requires a simpler on-chip platform design, because the laser beams replacing the uniform bias magnetic field lead to a more convenient and flexible experimental setup. Thus, the chip system could get rid of bulky Helmholtz coils and can be further integrated with tailored photonic waveguides.[12,13]
This paper is organized as follows. In Section 2, we describe the theories behind OFMTs and MW state-dependent potentials and analyze the combination of them on an atom chip. Then, in Section 3, we investigate microwave precise control of both internal and motional atomic states in OFMTs. Calculations of the potentials are presented to show that controlled state-sensitive collisional interaction between OFMTs could be achieved. In Section 4, we illustrate an array of individually addressable OFMTs for single atoms manipulation. A two-qubit phase gate operation via our proposed scheme is simulated. Finally, we summarize our design of integrated hybrid atom chips and discuss the possible applications in practical quantum technologies in the conclusion section.
2. Principle of designCombining optically induced magnetic and microwave fields to structure the complex potentials required for state-selective interaction on the atom chip is essential for our design. For on-chip trapping potential geometries, an OFMF acts the same as a real magnetic field but has better flexibility.[23,24] The Gaussian laser beam can be used to replace a pair of large Helmholtz coils for on-chip magnetic traps. Diverse concepts of trapping using fictitious magnetic fields have been proposed or experimentally demonstrated.[25–28] For coherent manipulation on atom chips, the microwave generated by coplanar waveguides is one of the most attractive tools. The MW state-dependent potential provides coherent and simultaneous control of both internal and motional states,[9] which lies at the heart of internal-state labeled paths interferometry[29,30] and atom-chip based quantum gates.[17]
As shown in Fig. 1, in the presence of a laser field tuned near the transitions of the D lines, the AC Stark shift of an alkali-metal atom in its ground state takes the approximate form[23]
where
gF is the Landé
g factor,
mF is the magnetic quantum number,
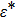
is a unit vector defining the laser polarization,
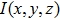
is the laser field intensity,
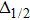
and
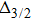
are the laser detunings from D1 and D2 transitions, respectively. When the laser field is circularly polarized and properly detuned, satisfying
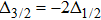
(the wavelength can be calculated to be about 790 nm), the AC Stark shift results in only a vector part analogous to a pure Zeeman shift. The direction of this effective field is parallel to the laser propagation axis, and its magnitude is proportional to the laser intensity
where
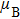
is the Bohr magnetron and
is the OFMF. Consider a Gaussian laser beam with a beam waist of
ω0 and a laser power of
P, then the effective magnetic field will distribute as the laser intensity and can be described as
According to Refs. [23, 24], and [27],  of laser intensity corresponds to a 35 G effective magnetic field. This OFMF could be directly superposed with a real magnetic field under the rule of vector operation. Since the laser light has special wavelength 790 nm between the D1 and D2 lines of rubidium atoms and large detuning, the photon scattering rate is low enough for effective long lifetime trapping.[25,26] In combination with the current-carrying wires’ produced static magnetic field, three-dimensional confinement magnetic traps can be formed above the atom chip.[26,27]
of laser intensity corresponds to a 35 G effective magnetic field. This OFMF could be directly superposed with a real magnetic field under the rule of vector operation. Since the laser light has special wavelength 790 nm between the D1 and D2 lines of rubidium atoms and large detuning, the photon scattering rate is low enough for effective long lifetime trapping.[25,26] In combination with the current-carrying wires’ produced static magnetic field, three-dimensional confinement magnetic traps can be formed above the atom chip.[26,27]
The concept of MW potentials is similar to that of optical potentials created by near resonant laser beams.[9,17] As shown in Fig. 1, a microwave field with a frequency  near the hyperfine splitting of 6.8 GHz and all polarization components is applied to the hyperfine states
near the hyperfine splitting of 6.8 GHz and all polarization components is applied to the hyperfine states  , leading to a “dressing” of the states with AC Zeeman shifts depending on F and mF.[17,29,30] Here we consider the weak-field-seeking sublevels
, leading to a “dressing” of the states with AC Zeeman shifts depending on F and mF.[17,29,30] Here we consider the weak-field-seeking sublevels  and
and 
where

is the frequency of the Rabi coupling and
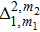
is the MW detuning from the resonance of the transition. Here we focus on the regime far MW detuning
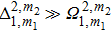
for all
m1 and
m2, which results in only weak coupling of the states

and excellent coherence property. From Eqs. (
4) and (
5), we can see that the AC Zeeman shift has opposite signs for
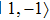
and
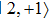
, giving internal-state dependence of the potentials in a controllable way.
Generally, the OFMTs can be formed at distances 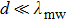 from the chip surface, where the maximum MW field gradients depend on d instead of
from the chip surface, where the maximum MW field gradients depend on d instead of 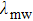 and the MW potentials vary on micrometer scale. Thus the atoms in the OFMTs can be manipulated with the MW potentials generated by coplanar waveguides on the chip. The total potential
and the MW potentials vary on micrometer scale. Thus the atoms in the OFMTs can be manipulated with the MW potentials generated by coplanar waveguides on the chip. The total potential  can be formed with versatile geometries which are required for controlled interactions and QIP on chip.
can be formed with versatile geometries which are required for controlled interactions and QIP on chip.
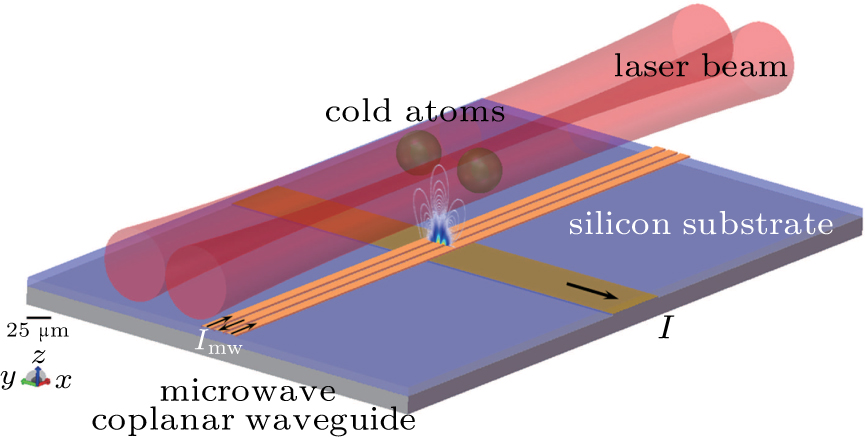
3. Controlled collisional interactionA common way to achieve entanglement and QIP with neutral atoms is to condition the interactions on the internal state by controlling the wavefunction overlap in a state-dependent way.[15] Such controlled coherent dynamics with collisional interactions can be achieved by OFMTs with MW potentials. As shown in Fig. 2, two circularly polarized 790 nm Gaussian laser beams propagate along the x axis, resulting in localized fictitious magnetic fields. The chip is designed with two layers of gold wires separated by a thin polyimide layer based on a high-resistivity silicon substrate. The current-carrying wire on the bottom layer provides the static magnetic field for the formation of OFMTs and the CPW integrated on the upper layer generates microwave near-fields for coherent manipulation.
The entire potential can be written as
We now calculate the potential with the following parameters: current I = 15 mA, laser power P = 30 mW, beam waist  , the two laser beams propagate
, the two laser beams propagate 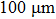 above the chip surface with a separation of 100
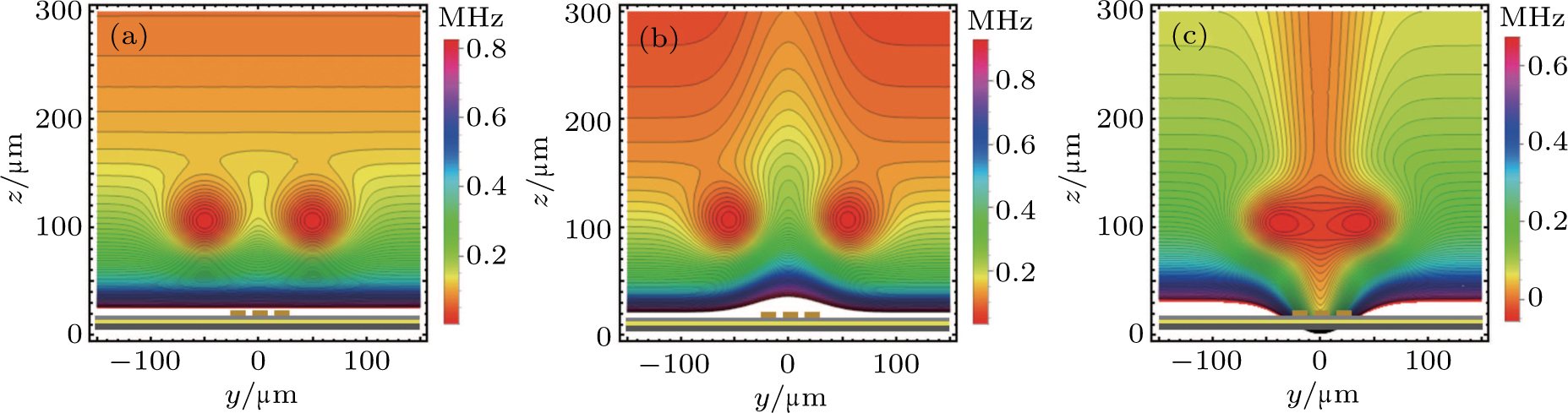
above the chip surface with a separation of 100  m between them. An Ioffe-type double-well OFMTs potential is formed with trap depths about
m between them. An Ioffe-type double-well OFMTs potential is formed with trap depths about  , the distribution of the OFMTs potential in the y–z plane is shown in Fig. 3(a). The geometry of the OFMTs can be adjusted simultaneously by changing the power and location of the laser beams. The center of the OFMTs can be easily traced along the Gaussian laser beam axis.
, the distribution of the OFMTs potential in the y–z plane is shown in Fig. 3(a). The geometry of the OFMTs can be adjusted simultaneously by changing the power and location of the laser beams. The center of the OFMTs can be easily traced along the Gaussian laser beam axis.
Then, an MW field is applied through the on-chip CPW on the upper layer. The three-wires CPW ( wire size,
wire size,  separation between wires) locates at the center between the two Gaussian laser beams, which carries quasi-static current
separation between wires) locates at the center between the two Gaussian laser beams, which carries quasi-static current  (center wire
(center wire  , ground wires
, ground wires 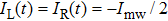 ). The detuning of the MW field from the transition
). The detuning of the MW field from the transition  is
is 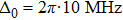 . State
. State  experiences an MW repulsive potential which increases the separation between the double-well OFMTs, while the MW attractive potential removes the barrier of the double-well OFMTs for state
experiences an MW repulsive potential which increases the separation between the double-well OFMTs, while the MW attractive potential removes the barrier of the double-well OFMTs for state  simultaneously, as shown in Figs. 3(b) and Fig. 3(c), respectively.
simultaneously, as shown in Figs. 3(b) and Fig. 3(c), respectively.
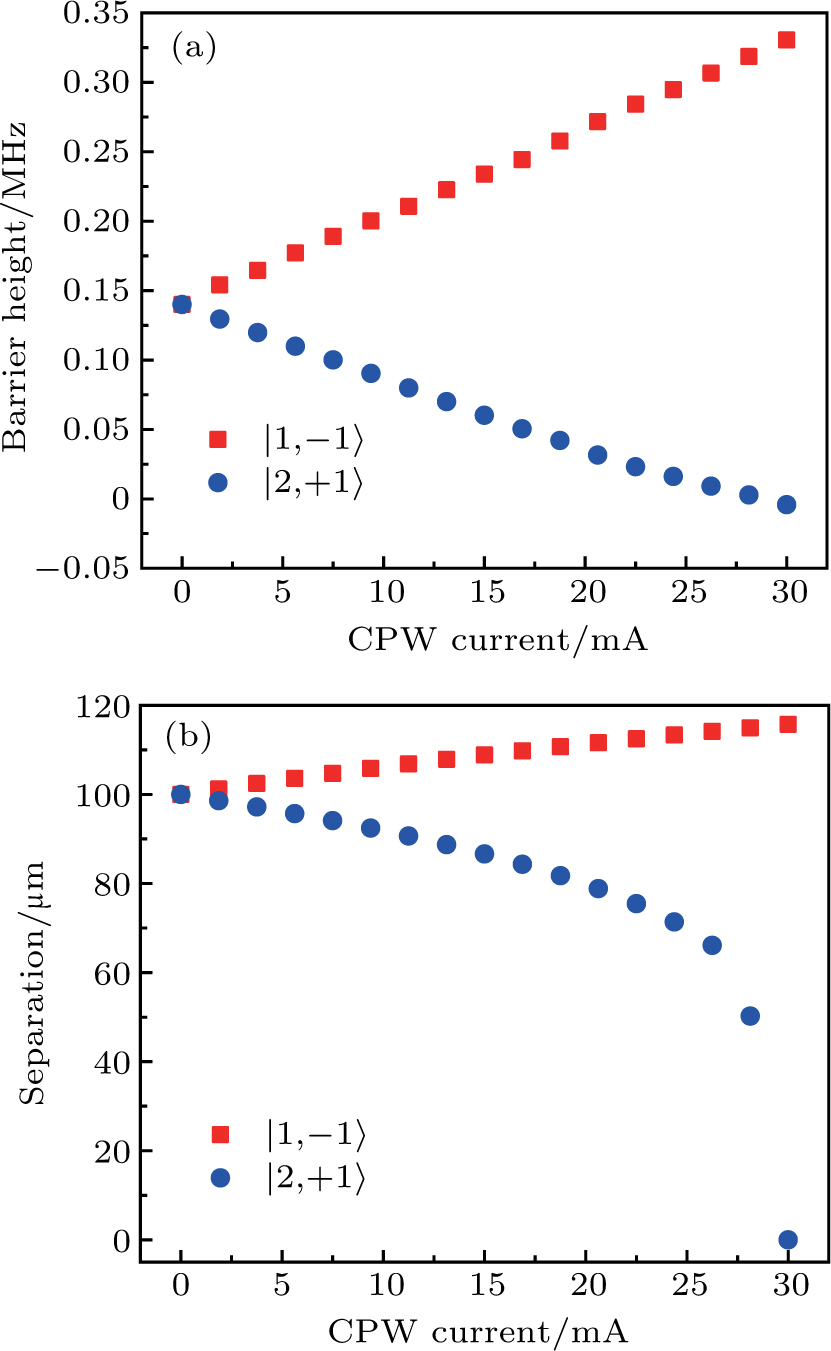
The barrier height and the separation distance are shown as a function of the MW field intensity in Fig. 4. By smoothly modulating the MW field intensity, we can control the minima of the double-well potential with high accuracy. Consider two trapped BECs in motional ground states and initialized in a coherent superposition of states 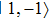 and
and 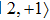 in the double-well OFMTs. A schematic diagram (Fig. 5) shows the controlled collisional dynamics in this designed potential geometry. The MW potential displaces the wavefunction selectively, introducing a wavefunction overlap for state
in the double-well OFMTs. A schematic diagram (Fig. 5) shows the controlled collisional dynamics in this designed potential geometry. The MW potential displaces the wavefunction selectively, introducing a wavefunction overlap for state  while shifting the wavefunction further apart for state
while shifting the wavefunction further apart for state 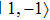 . The fidelity of the coherent dynamics is very close to one for a wide range of parameters, even at finite temperatures. The fidelity related to temperature as
. The fidelity of the coherent dynamics is very close to one for a wide range of parameters, even at finite temperatures. The fidelity related to temperature as 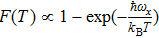 [15] is estimated to be better than 0.997 for a temperature
[15] is estimated to be better than 0.997 for a temperature 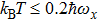 . This corresponds to a BEC temperature
. This corresponds to a BEC temperature 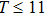 nK for our realistic confinement potentials with the axial trap frequency
nK for our realistic confinement potentials with the axial trap frequency  , which is physically achievable on a chip. Such coherent dynamics combined with state-sensitive collisional interactions enables high-fidelity entanglement generation for BECs in the double-well OFMTs potential.[9,31,32]
, which is physically achievable on a chip. Such coherent dynamics combined with state-sensitive collisional interactions enables high-fidelity entanglement generation for BECs in the double-well OFMTs potential.[9,31,32]
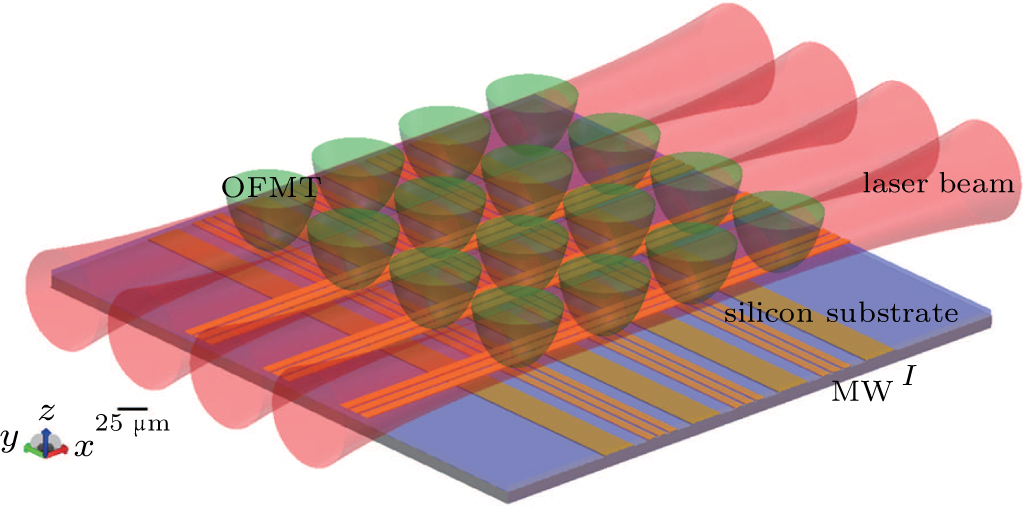
By applying micro- and nano-lithography techniques, the Gaussian laser beams can be integrated on a chip with fiber optics and photonic waveguides.[12–14] Thus, the double-well OFMTs geometry is expected to be extended to a tailored lattice-like structure (as displayed in Fig. 6). As it is seen from the calculations above, microfabricated CPWs can be used for site-selective manipulations between adjacent sites parallelly. Each site can be addressed individually via the accessible parameters such as the current on the wires and the laser intensity.[27] In this case, the controlled dynamics scheme on chip is scalable, which meets the requirement in developing quantum devices.
4. Phase gate operationThe conditional dynamics scheme can be applied for the implementation of a two-qubit collisional phase gate with neutral atoms on chip.[15–18] However, deterministic preparation of single neutral atoms in the motional ground state of chip traps remains to be the major challenge in the realization of the proposed gate schemes. As our earlier designed photonic chip for manipulating an array of single neutral atoms,[13] we can reduce the trapped atoms from large ensembles down to individual atoms for atom-chip quantum gates (as required for QIP). Here we design a tailored-waveguide based photonic chip for quantum phase gate operation based on collisional interactions between an array of individually addressable single atoms. The 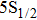 ground-state hyperfine levels of 87Rb
ground-state hyperfine levels of 87Rb  and
and  are an ideal choice as qubit basis states since both states are magnetically trappable and possess excellent coherence properties. Long coherent time could be obtained by applying a magic-intensity trapping technique[33] in the single atomic trap.
are an ideal choice as qubit basis states since both states are magnetically trappable and possess excellent coherence properties. Long coherent time could be obtained by applying a magic-intensity trapping technique[33] in the single atomic trap.
The chip consists of a silicon-substrate wire chip and a photonic chip with integrated waveguides. At the center of the photonic chip, an array of 4- doped silica waveguide cores spaced by
doped silica waveguide cores spaced by 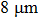 are embedded in a layer of silica cladding (
are embedded in a layer of silica cladding (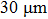 above the CPWs wire chip). These waveguides flare out at the input interface of the chip so that the optical fibers can be connected. An optimized refractive index contrast of about 0.7% is chosen to give single-mode operation at 790 nm. Phase Fresnel microlens with a focal length of about
above the CPWs wire chip). These waveguides flare out at the input interface of the chip so that the optical fibers can be connected. An optimized refractive index contrast of about 0.7% is chosen to give single-mode operation at 790 nm. Phase Fresnel microlens with a focal length of about  are etched at the output edges of each of the optical waveguides. Between each two waveguides, there are three wire CPWs (wire size
are etched at the output edges of each of the optical waveguides. Between each two waveguides, there are three wire CPWs (wire size  , separation between wires
, separation between wires 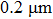 ) on the silicon-substrate wire chip. Under the CPWs wire layer, a stationary current carrying wire located at the bottom layer provides the axial magnetic confinement for the OFMTs. The schematic of the chip is shown in Fig. 7.
) on the silicon-substrate wire chip. Under the CPWs wire layer, a stationary current carrying wire located at the bottom layer provides the axial magnetic confinement for the OFMTs. The schematic of the chip is shown in Fig. 7.
We perform simulation of the lights propagating through the waveguides and microlens using Rsoft’s beam propagation method (BPM) package,[34] which shows good propagation characteristics (see Fig. 7(c)). When independent 790 nm laser beams are coupled into the waveguides, combining with the current-carrying wire on the bottom chip, an array of OFMTs are formed at the beam waists. Since the laser beams are focused with a beam waist of about  , the OFMTs have extremely small trap volumes, within the regime of collision blockade effect. Thus only one atom can be trapped in each OFMT and an array of single atoms can be obtained for QIP.
, the OFMTs have extremely small trap volumes, within the regime of collision blockade effect. Thus only one atom can be trapped in each OFMT and an array of single atoms can be obtained for QIP.
Single-qubit preparation and rotation can be easily implemented by coupling the states  and
and  through a two-photon simulated Raman transition. The coherent Raman lights propagating through the independent waveguide will only manipulate the corresponding atom without affecting the states of the neighboring atoms. The microlens can collect the fluorescence from the corresponding trapped atom, thus qubits addressing and state detection can be accomplished through the individual waveguides.
through a two-photon simulated Raman transition. The coherent Raman lights propagating through the independent waveguide will only manipulate the corresponding atom without affecting the states of the neighboring atoms. The microlens can collect the fluorescence from the corresponding trapped atom, thus qubits addressing and state detection can be accomplished through the individual waveguides.
A fundamental two-qubit quantum gate for QIP can be implemented by modulating the trapping potential state selectively.[15,17] Here we utilize on-chip CPWs providing state-dependent potentials to control the two atoms interaction, resulting in a collisional phase shift π if and only if both are in state  . The quantum phase gate is described by the evolution operator
. The quantum phase gate is described by the evolution operator
for the four two-qubit basis states. With the following realistic parameters: current
I = 24 mA, laser power
P = 1 mW, beam waist

, MW detuning
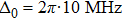
, CPW center-wire current
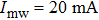
, we simulate the trapping potentials variation for the states
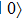
and
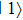
and show the process of the phase gate operation. The magnetic field at the trap center is
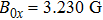
, where the first-order differential Zeeman shift equals zero and the coherence time could be maximized to be of the order of seconds.
[9,33] The three-dimensional OFMTs provide tight harmonic confinements with axial trap frequencies
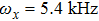
and transverse trap frequencies

. As shown in Fig.
8, we select single atoms in sites 2 and 3 as phase gate qubits by applying quasi-static currents on the CPW between them. Due to the strong transverse confinement provided by the optically induced magnetic field, the MW manipulation will not influence other sites. The state-dependent microwave potentials appropriately displace the potential minima of sites 2 and 3, resulting in a collisional phase shift
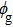
for qubit state

, while the unwanted collision for state

limiting the fidelity is avoided. By modulating the MW intensity, the qubit state
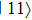
will oscillate and collide during each cycle.
[17,35] After several cycles of oscillations, a desired phase shift
π is accumulated and a phase gate operation is achieved. Such gate operation can be applied to arbitrary two adjacent sites through the CPW between them.
There are several mechanisms which could possibly destroy the fidelity. However, the induced infidelity from these system error sources can be suppressed to the order of a few 10−3 by optimization of the potential parameters and better control of the gate dynamics. First, the probabilities of the occupation of relative motion excited states corresponding to finite temperature will lead to a reduction of fidelity. As discussed above in Section 3, at a temperature 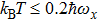 , the fidelity remains of the order of 99.7%. Second, another important mechanism is the possibility of trap loss and decoherence of the qubits during the operation, which is dominated by the chip surface thermal effect. Here we utilize OFMF tight confinements with less current-carrying wires on chip at a distance of about
, the fidelity remains of the order of 99.7%. Second, another important mechanism is the possibility of trap loss and decoherence of the qubits during the operation, which is dominated by the chip surface thermal effect. Here we utilize OFMF tight confinements with less current-carrying wires on chip at a distance of about  from the surface for the chip layout shown in Fig. 7, then the surface thermal effect is expected to be dramatically reduced. Furthermore, the magnetic field at the trap center is set to
from the surface for the chip layout shown in Fig. 7, then the surface thermal effect is expected to be dramatically reduced. Furthermore, the magnetic field at the trap center is set to  , where the first-order differential Zeeman shift equals zero and the coherence time could be maximized. Following the treatment of Ref. [17], we can estimate an overall trap lifetime
, where the first-order differential Zeeman shift equals zero and the coherence time could be maximized. Following the treatment of Ref. [17], we can estimate an overall trap lifetime 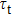 and coherence lifetime
and coherence lifetime 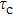 better than 1 s, leading to an error of
better than 1 s, leading to an error of 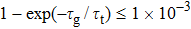 at a gate operation time of
at a gate operation time of  . In addition, the transverse excitations due to collisions of the atoms will result in an additional distortion of the wave function. To avoid this effect, the trap geometry is designed to be a three-dimensional anisotropic harmonic oscillator potential, with
. In addition, the transverse excitations due to collisions of the atoms will result in an additional distortion of the wave function. To avoid this effect, the trap geometry is designed to be a three-dimensional anisotropic harmonic oscillator potential, with  . The single atoms are initially cooled to transverse ground states with kinetic energies
. The single atoms are initially cooled to transverse ground states with kinetic energies 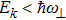 . In this case, the gate operation can be considered as one-dimensional dynamics and the probability of transverse excitation is suppressed to a negligible value. Finally, the fluctuations of the trap potentials and MW potential will also introduce noise into the gate dynamics. Fortunately, with stable current sources (magnetic and MW fields) and laser fields (an available stability on the level of 10−5), the field noise-induced phase fluctuations can be controlled at the quantum projection noise level.[9] Overall, we conclude that for optimized geometries, optimal operation control error rates of the order of 10−3 should be possible in our atom–chip system with present day technology. Thus, high fidelity and scalable gate operations in an array of OFMTs are obtainable.
. In this case, the gate operation can be considered as one-dimensional dynamics and the probability of transverse excitation is suppressed to a negligible value. Finally, the fluctuations of the trap potentials and MW potential will also introduce noise into the gate dynamics. Fortunately, with stable current sources (magnetic and MW fields) and laser fields (an available stability on the level of 10−5), the field noise-induced phase fluctuations can be controlled at the quantum projection noise level.[9] Overall, we conclude that for optimized geometries, optimal operation control error rates of the order of 10−3 should be possible in our atom–chip system with present day technology. Thus, high fidelity and scalable gate operations in an array of OFMTs are obtainable.
5. ConclusionWe have proposed a novel on-chip platform for controlling and manipulating cold atoms precisely and coherently. This new simple scheme makes use of OFMF and MW state-dependent potentials integrated on an atom–chip system. We have shown various trapping potential geometries which could be applied to coherently control both the internal states and the external states of cold 87Rb atoms with high accuracy and high fidelity. Our designs and fabrications have concentrated on the applications such as entanglement generation and controlled collisional phase gate operation. The realization of such hybrid atom chip systems is a subject of experimental efforts in future work, which will be helpful in developing compact integrated devices for quantum engineering and QIP.