† Corresponding author. E-mail:
In the present work, the effects of Ni atoms and vacancy concentrations (0.1%, 0.5%, 1.0%) on the formation process of Cu solute clusters are investigated for Fe–1.24%Cu–0.62%Ni alloys by molecular dynamics (MD) simulations. The presence of Ni is beneficial to the nucleation of Cu precipitates and has little effect on coarsening rate in the later stage of aging. This result is caused by reducing the diffusion coefficient of Cu clusters and the dynamic migration of Ni atoms. Additionally, there are little effects of Ni on Cu precipitates as the vacancy concentration reaches up to 1.0%, thereby explaining the embrittlement for reactor pressure vessel (RPV) steel. As a result, the findings can hopefully provide the important information about the essential mechanism of Cu cluster formation and a better understanding of ageing phenomenon of RPV steel. Furthermore, these original results are analyzed with a simple model of Cu diffusion, which suggests that the same behavior could be observed in Cu-containing alloys.
The nucleation and growth of Cu-rich clusters have been proved to play an important role in the microstructural and mechanical properties in RPV steel. Dislocation glide is impeded and yield strength is increased due to the formation of Cu clusters, which leads to the embrittlement in RPV steel.[1,2] The continuous irradiation by fast neutrons causes a super-saturation of vacancies and self-interstitials and enhances the diffusion of Cu, which occurs via the vacancy mechanism. Over the last sixty years, Cu precipitates have been extensively studied in experiment and theory. In the experimental aspect, small-angle x-ray neutron scattering,[3] transmission electron microscopy (TEM),[4,5] atom probe tomography (APT),[6,7] etc. have been utilized to analyze the structural, compositional, and morphological evolutions of Cu precipitates.[8–15] In the theoretical aspect, multi-scale simulations have been performed to study the formation and evolution of Cu-rich clusters or precipitates, phase transition, Cu diffusion in α-Fe[16–22] and interactions between Cu clusters and vacancies.[23–33]
Investigations have shown that Cu nano-clusters may consist of not only pure Cu but also complexes, such as CumNin clusters,[29,31] which have the lower formation energies than that of pure Cu cluster.[19,34] In general, the literature data show that the main function of Ni atoms in the Cu-contained ferric alloys can accelerate the precipitation of Cu clusters[35–37] and increase the quantity of Cu clusters[38] during ageing. High vacancy concentration can also increase Cu clusters precipitating.[39] However, according to Wang et al.’s study,[40] Ni atom has a temporal delay effect on Cu precipitate with a specific behavior of inhibiting Cu precipitation during ageing, which is poorly explained. Moreover, recently published calculations only focus on the influence of vacancy concentration or Ni atom on Cu precipitate, and few studies show consideration of the interaction between vacancy concentration and Ni atom for Cu precipitate on an atomic scale.
In the present work, MD simulations are employed to investigate the influences of vacancy concentration and Ni atom on the formation process of Cu solute cluster in Fe–Cu–Ni ternary alloy. The diffusion coefficient as well as the size of Cu cluster is calculated to evaluate the Cu diffusivity. Results of Fe–Cu–Ni alloy and Fe–Cu alloy under different vacancy concentrations are compared to explain the promotion and inhibition effect of Ni atom on Cu precipitation with ageing time increasing. Ni atoms accelerate Cu precipitation at the nucleation stage, while inhibit Cu precipitation at the coarsening stage. Moreover, for the alloy with 1.0% vacancy concentration, Ni atoms, compared with vacancy concentration, have little effect on Cu diffusion. These results provide important information about essential mechanism for Cu enriched cluster formation to understand ageing phenomenon of RPV steel.
The MD simulations are carried out by using the large-scale atomic molecular massively parallel simulator (LAMMPS) code.[40,41] For metals, the interaction between atoms are typically described by the embedded-atom method (EAM) potential. The Fe–Cu–Ni EAM potential,[35] which is well suitable for the present study, is employed to describe the alloy thermodynamic properties and the interactions between solute atoms and point defects. The equilibrium solubility of Cu in Fe-matrix, obtained through this potential agrees well with the experimental value.
Cu clusters in Fe–1.24%Cu–0.62%Ni (Fe–Cu–Ni) alloys with vacancy concentrations of 0.1% (0.1%v), 0.5% (0.5% v), and 1.0% (1.0% v), and in Fe–1.24%Cu (Fe–Cu) alloys with vacancy concentrations of 0.1% (0.1% v) and 1.0% (1.0% v) have been studied at 773 K. All percentages mentioned in this paper are atomic percentages unless otherwise stated. The vacancy concentration values of about 0.1% to 1.0% adopted in this paper are necessary, because otherwise MD simulations would be too slow. According to previous studies,[42] the vacancy concentration range is rational, which does not change the Cu cluster formation mechanism. A cubic simulation cell containing the bcc-Fe lattice with x direction, y direction, and z direction parallel to the [100], [010], and [001] axes is constructed. The dimensions of the cube are 
| Table 1.
General conditions of the molecular dynamics (MD) simulations. . |
In the present work, the radial distribution function (RDF) is calculated to indicate the phase transition process. The mean square displacement (MSD) of Cu atoms is calculated to indicate the diffusion process. The MSD is defined by the following equation:[27]
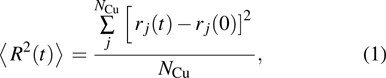 |

The diffusion coefficient 
 |
In order to analyze the evolution of Cu cluster, the size and atom number of Cu cluster are determined based on the study of Miller.[46] The cutoff distance for the interatomic potential is equal to 4.0 Å. This value is determined by the third nearest neighbor interaction of Cu atom. That is to say, atoms whose interatomic distance is less than 4.0 Å are considered to have interatomic interactions and form Cu cluster. Cux is defined as the number of Cu atoms contained in a Cu cluster, which is equal to or greater than x. Cumax represents the number of Cu atoms contained in the largest cluster and CuNimax represents the atom number in maximum co-composed cluster of Cu atoms and Ni atoms.
The MSDs of Fe, Cu, and Ni atoms in Fe–Cu–Ni ternary alloy with a vacancy concentration of 0.1% at 773 K are shown in Fig.
 | Fig. 1. (color online) (a) MSDs of Fe, Cu, Ni atoms in Fe-1.24% Cu-0.62% Ni alloy with vacancy concentration of 0.1%, (b) MSDs of Fe, Ni atoms in Fe-0.62% Ni alloy with vacancy concentration of 0.1%. |
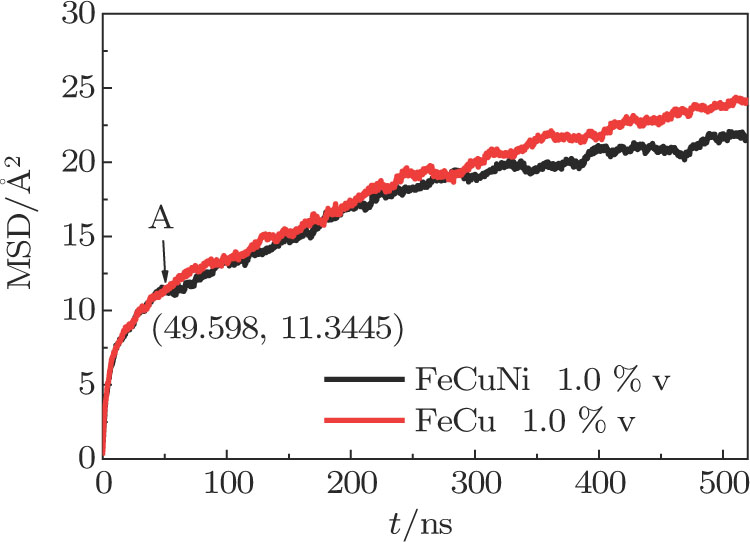
The Cu MSD curves in Fe–Cu–Ni and Fe–Cu alloys with a vacancy concentration of 0.1% are shown in Fig.
 | Fig. 2. (color online) MSDs of Cu atoms in Fe-1.24% Cu-0.62% Ni and Fe-1.24% Cu alloys with vacancy concentration of 0.1%. |
From the above discussion, we know that Cu atoms and Ni atoms interact with each other during the formation of Cu precipitates in Fe matrix. So we divide the Cu diffusion into three stages according to different interaction behaviors between Cu and Ni atoms. Stage I is for the free diffusions of Cu and Ni atoms, stage II is for the mutual promotion between Ni and Cu atoms, and stage III is for the inhibition of Ni atoms on Cu diffusion. These three stages correspond to 0–A segment, A–B segment, and B afterward segment in Fig.
The composition of Cu precipitates during ageing has been debated for a long time. The classical theory of nucleation predicts the formation of precipitates with a composition close to the equilibrium one, i.e., the formation of almost pure Cu cluster. In order to give an in-depth insight into the influence of Ni on the formation of Cu cluster, the specific configurations of Cu and Ni atoms are shown in Fig.
Figures
From region II through Figs.
Ni segregates into the core region of the precipitate at the initial formation stage and can be pushed away from the core towards the interface of the precipitates for the following growth stage. This is consistent with phase field,[53] first principles[54] and Langer–Schwartz[38] simulations. These phenomena were also observed experimentally.[51,55]
To compute the size of precipitate in the simulations, we only take into account clusters, in which the number of solute atoms is more than four, connected with at least one nearest neighbor bond. The exact value of this critical size does not significantly affect the results for time above 1 fs — it does not change, in particular, the comparison with experimental results. Figure
The MSD curves of Cu with three different vacancy concentrations in Fe–Cu–Ni ternary alloys are shown in Fig. 

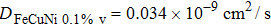
 | Fig. 5. (color online) Time-dependent MSDs of Cu atoms in Fe–1.24%Cu–0.62% Ni alloys with vacancy concentration of 0.1%, 0.5%, and 1.0%. |
| Table 2.
Intersections of Cu MSDs with different vacancy concentrations of Fe–1.24%Cu–0.62% Ni alloys. . |
In order to reveal what has happened more clearly around intersections with different vacancy concentrations of Fe–Cu–Ni alloys, 
 | Fig. 6. (color online) Partial pair distribution functions  |
Figure 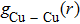

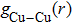
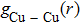
The Cu4, Cumax, and CuNimax in Fe–Cu–Ni alloys with different vacancy concentrations are shown in Fig.
From Fig.
 | Fig. 8. (color online) Time-dependent MSDs of Cu, Ni, and Fe atoms in Fe–1.24%Cu–0.62% Ni alloys with vacancy concentrations of 0.1% and 1.0%. |
Figure
Based on molecular dynamics simulation, the influence of vacancy concentration and Ni solute atoms on Cu precipitate in Fe–1.24%Cu–0.62% Ni during ageing are investigated. Ni atoms accelerate Cu precipitation at the nucleation stage, while inhibit Cu precipitation at the coarsening stage. The atom number and size of Cu cluster correspondingly increase with vacancy concentration from 0.1% to 1.0%. As the vacancy concentration increases to 1.0%, Ni atoms have little effect on the process of Cu diffusion compared with vacancy concentration.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] |