† Corresponding author. E-mail:
The thermal failure induced by high power microwave (HPM) in a complementary metal oxide semiconductor (CMOS) inverter is investigated and its dependence on microwave parameters is discussed in detail. An analytical model of the temperature distribution is established and the relationships between hotspot temperature and pulse width and between hotspot temperature and frequency are predicted, which reveals a more severe rise in temperature under the influence of microwave with longer width and lower frequency. The temperature variation mechanism and the theoretical temperature model are validated and explained by the simulation. Furthermore, variation trend of damage threshold with microwave parameters is derived theoretically, and the conclusions are consistent with simulation results and reported data.
As the integrated circuit is used more and more widely in civil and military fields, research on microelectronic reliability has been a hotspot in recent years. The failures caused on the semiconductor could be various, such as a material defect, device aging and radical external excitation. High power microwave is a typical instance of electromagnetic interference with a high power level, high frequency and short width generally, and is developed rapidly for the use of microwave weapons. High power microwave (HPM) is easy to couple into electronic system via antennas, cables and apertures of shells intentionally or unintentionally, leading to degeneration in performance and temporary or permanent failure.[1]
Since the external microwave may induce a catastrophic impact, the microwave effects on various integrated circuits and semiconductors have widely been investigated in these last few years. Many experimental researches were carried out through testing the damage susceptibility of discrete PIN diode,[2] high electron mobility transistor (HEMT),[3,4] bipolar transistor,[5] integrated components on transistor–transistor logic (TTL) and CMOS logic,[6] computer system,[7] etc. Besides, theoretical studies were also presented widely. Ren et al. reported the motion of current filaments and the thermal failure effect of PIN diode under electromagnetic pulse.[8] Liu et al.[9,10] and Yu et al.[11,12] revealed the phenomena of damage and degradation as well as their mechanisms of GaAs HEMT under the influence of HPM by numerical simulation and experiment used for comparison. Chai et al.[13] and Ma et al.[14–16] proposed the thermal failure mechanism in bipolar semiconductor and proposed some measures against it. As for the CMOS device, Kim and Iliadis focused on the dynamic and static characteristics in a CMOS inverter under HPM environment.[17–20] Wang et al.[21] and Yu et al.[22–24] researched the HPM induced latch-up effect and its critical factors in experiment and theory. However, the thermal damage is also a significant failure cause for the CMOS device besides latch-up.[1]
This work focuses on the thermal failure in the CMOS inverter caused by HPM. An analytical temperature distribution is derived and the relationships between hotspot temperature and microwave frequency, and between hotspot temperature and width are predicted. Based on numerical simulation, the damage mechanism is presented and the temperature model is validated and explained. In addition, the variations of damage threshold with frequency and width are predicted and compared with simulation results and reported data.
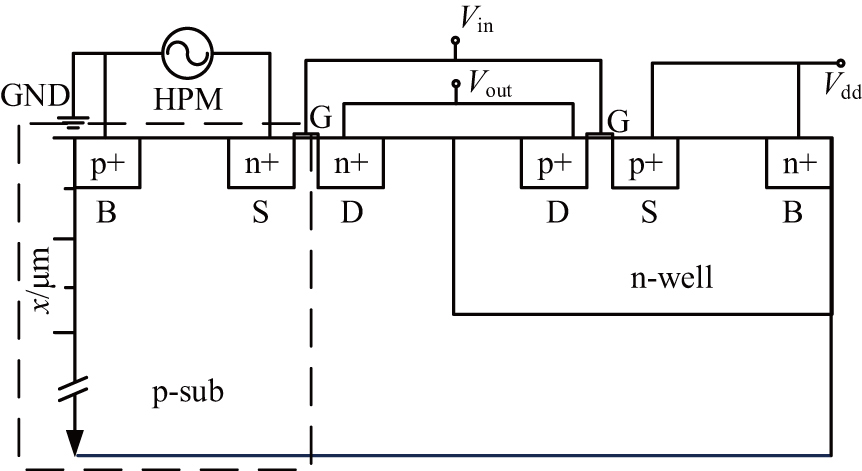
A typical CMOS inverter schematic diagram with an n-well is depicted in Fig.
Obviously, during the positive semi-period of the external microwave, the PN junction across the bulk and source terminal becomes biased reversely, and there is only reverse current which can be ignored since an avalanche effect has not been taken into consideration. However, when the external electric potential turns negative, current paths from the bulk and source terminal near the device surface occur, leading to a Joule heat production. In this case, the temperature of this region will rise up if the heat cooling rate is less than the heat generation rate. Thus, the surface temperature presents a periodic “down-up-down” variation, and the device maybe burns out at the hotspot finally.
According to the above analysis, the rise in device temperature is due to the forward current across the “N
 |
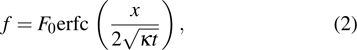 |
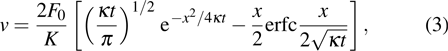 |
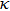

 |
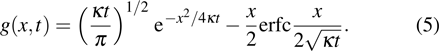 |
According to our previous discussion, the hotspot exists at the surface of the device, hence the max temperature is located at x = 0, and equation (
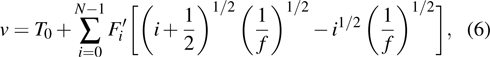 |
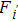
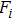

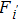
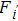
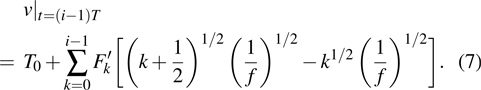 |
Therefore, equation (
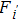
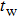


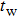
 |
One thing should be noted, i.e., the injection power level is assumed to be a constant value in the above discussion, whereas it contributes to 
In order to verify the validity of the above analysis, it is necessary to understand the temperature distribution inside the device in practice. Unfortunately, it is not easy to capture the temperature distribution in detail in a real semiconductor device, therefore, a simulation model is built and the phenomena are discussed physically on the basis of it in our work. The device structure is modeled (referring to Fig. 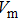
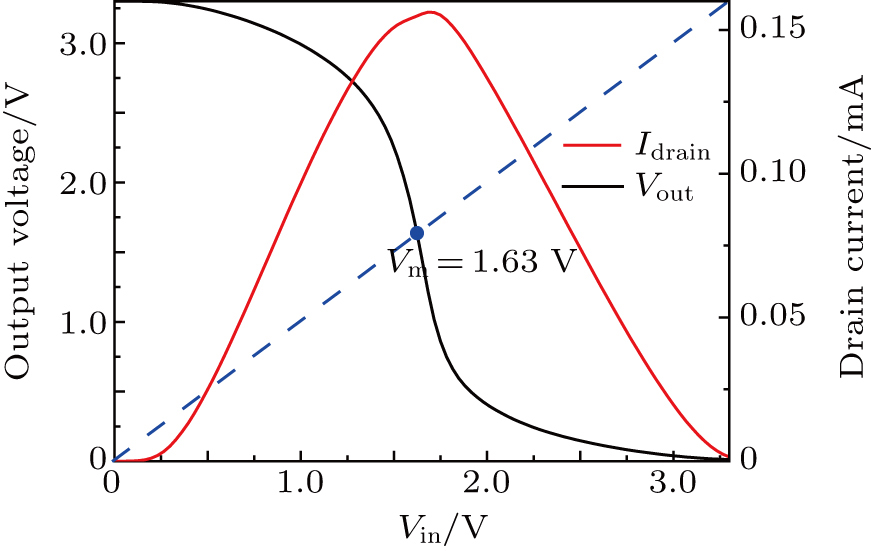
The maximum temperature inside the CMOS inverter responding to the injected microwave with a peak induced voltage of 5 V is shown in Fig. 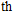

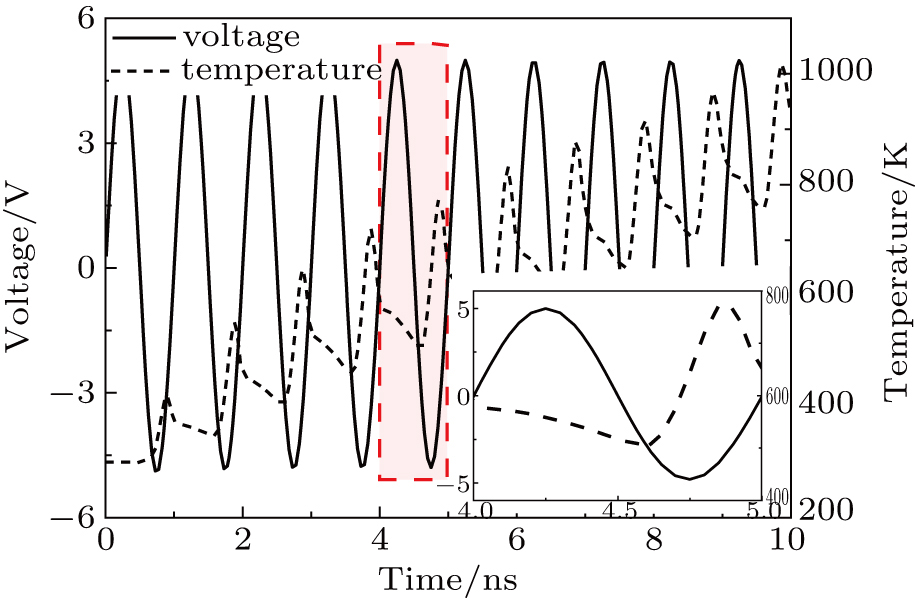 | Fig. 3. (color online) Variation of max temperature with time under the action of external stimulating microwave. |
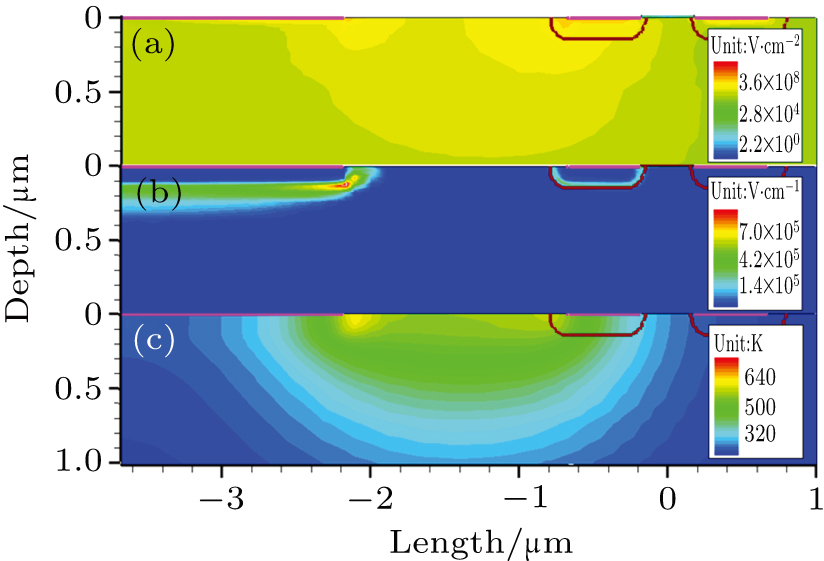 | Fig. 4. (color online) Distributions of (a) current density, (b) electric field strength, and (c) temperature during positive semi-period of external microwave inside the device. |
 | Fig. 5. (color online) Distributions of (a) current density, (b) electric field strength, and (c) temperature during negative semi-period of external microwave inside the device. |
Obviously, when the external electric potential is positive, the junctions of N
Equation (
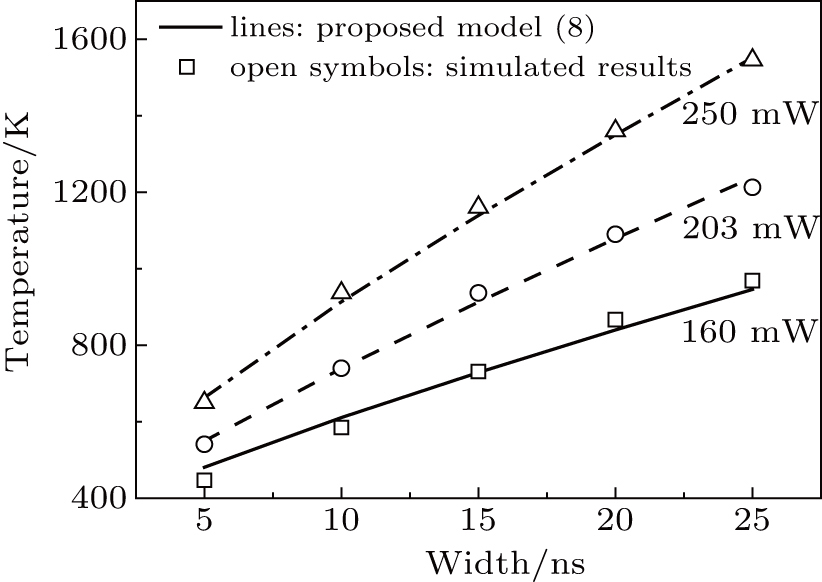
Besides, the relationship between max temperature and microwave pulse width is obtained by simulation and shown in Fig.
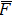
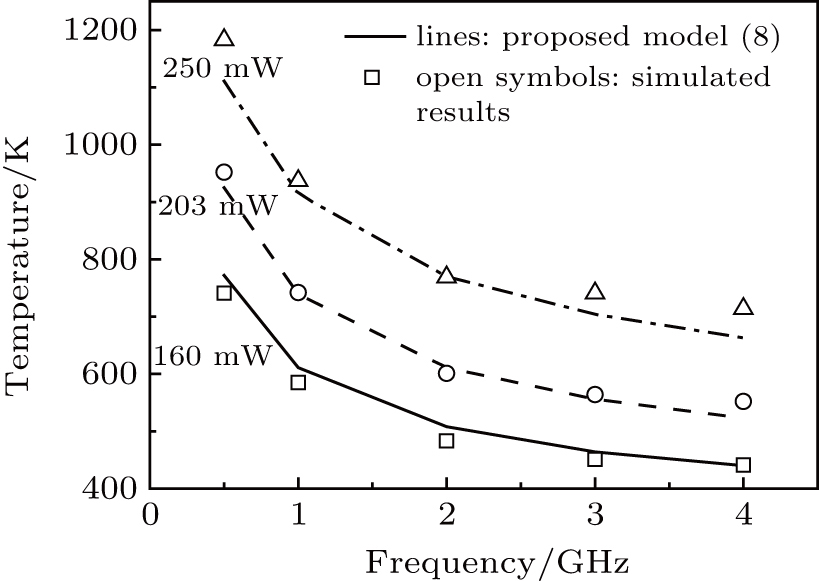
As mentioned in Section 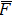
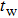

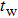
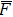
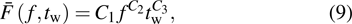 |
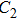
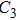
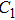
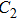
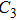
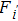
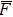
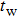
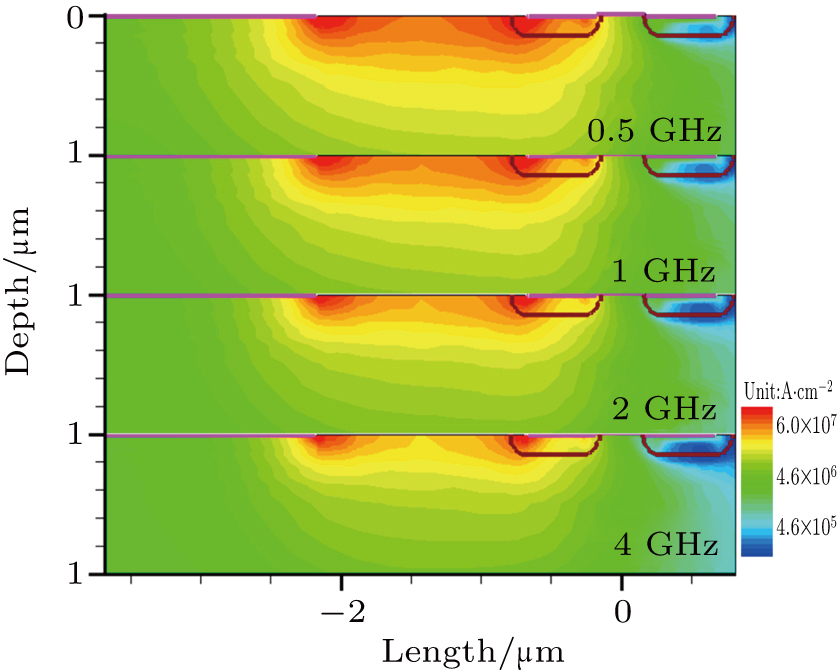 | Fig. 8. (color online) Forward current densities under diverse frequency microwaves after the same period of time. |
Furthermore, for a microwave with a lower frequency, the duration of each cycle is longer, and the temperature of the hotspot is larger after a temperature-rise period, leading to a larger junction current for the next cycle in turn. After the same period of time, the temperature and the current density are both higher for lower frequency, resulting in a larger 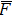
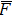
As we mentioned in Section 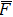
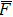

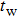
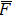

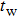
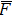
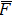
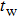
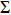


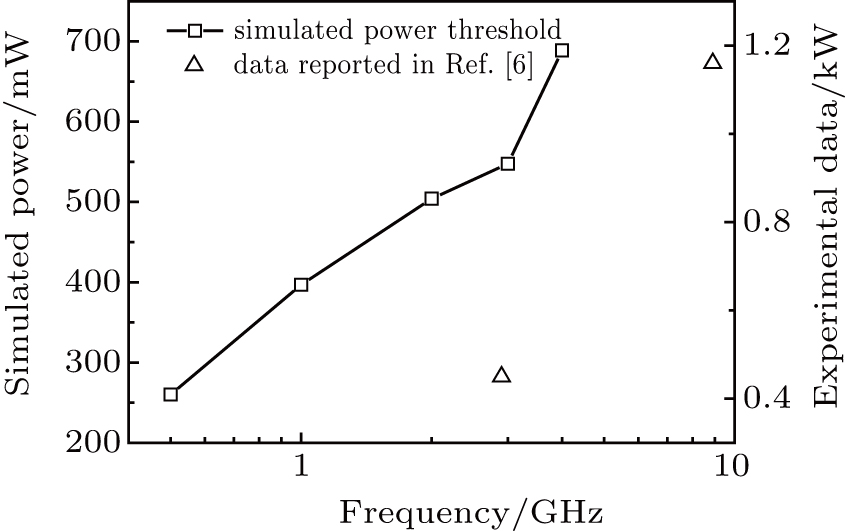 | Fig. 9. Variations of simulated (empty square) and measured (empty triangle) damage power threshold with frequency. |
A temperature rising behavior for a typical CMOS inverter under the influence of high power microwave is derived theoretically on the basis of an abstract model, and analytical hotspot temperature inside the device is presented with considering the dependence on microwave frequency and pulse width. By numerical simulation on the device model built in this work, the mechanism of temperature variation in the device is presented and the results show that forward current acts as a major heat source during the negative semi-cycle of external microwave. The simulated temperature variation trends validate the dependence on pulse width and frequency we predicted from the theoretical model, and the relationship between equivalent external heat flux and microwave parameter is explained. Furthermore, the dependence of damage threshold on frequency and width is derived based on the theoretical model, and turns out to be consistent with simulated results and reported conclusions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |