† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61505074), the National Basic Research Program of China (Grant No. 2013CBA01703), the HongLiu Young Teachers Training Program Funded Projects of Lanzhou University of Technology, China (Grant No. Q201509), and the National Undergraduate Innovation Training Program of China (Grant No. 201610731030).
A method for fabricating a micro-optical structure based on sample rotation and two-laser-beam interference is proposed. The rotation process is analyzed using the coordinate transformation in matrix presentation and the theoretical expressions of the optical field distributions corresponding to different sample rotations. By rotating the samples and changing the laser wavelength, various special micro-optical structures can be obtained, such as equally spaced concentric rings and irregular trapezoidal lattices; these structures are demonstrated by simulating the corresponding optical field distributions. The proposed approach may be developed into a low-cost laser interference lithography technology for the fabrication of various micro-optical structures.
Micro-structures have numerous applications, such as in photonic crystals,[1] grating structures,[2] and biosensors.[3] In fact, several micro- and nano-structure fabrication methods have been developed to date, including nano-imprinting, ion-beam lithography (IBL), electron-beam lithography (EBL),[4] x-ray lithography,[5] and atomic force microscope lithography.[6] However, these technologies have a great number of disadvantages in terms of cost, efficiency, and the complexity of the manufacturing process.[7–10] Recently, surface plasmonic lithography[11–13] has been widely studied, as this technique allows fabrication of sub-wavelength structures. In the previous works by the present authors,[14–16] waveguide-mode interference lithography was proposed and presented; this technique can be used to fabricate sub-wavelength gratings with different periods. However, as regards to micro-structure fabrication, including periodic one-dimensional (1D) and two-dimensional (2D) structures, the most commonly used method is laser interference lithography (LIL).[17–22] For example, Jiang et al. fabricated 1D and 2D superhydrophobic graphene surfaces by means of two-laser-beam interference;[23] Xuan et al. obtained periodic triangle truncated pyramid arrays using an LIL system;[24] and moth-eye structures were fabricated on silicon via six-laser-beam interference lithography by Xu et al.[25]
In general, two-laser-beam interference can be used to fabricate simple periodic 1D micro-optical structures. For more complex structures, additional laser beams may be required;[26,27] however, this may complicate the optical devices and increase the operation difficulty. Thus, improvements to the LIL technology and cost performance are also required.[28] Recently, Wang et al. fabricated a 2D-lattice optical structure by rotating a sample by 90° after the initial exposure to expose it for a second time.[29] Furthermore, Hassanzadeh et al. proposed the fabrication of a large number of interesting microstructures, such as equally spaced concentric rings,[30] using multi-exposure LIL based on the rotation of a Lloyd’s mirror interferometer. However, it is difficult to rotate that type of interferometer, and the lithography principles and rotation process involved in the proposed approach have not been widely examined.
In this paper, we propose the use of two-laser-beam interference with two different kinds of photoresist-sample rotation methods for the fabrication of varieties of micro-optical structures with latent application. Based on the coordinate transformation in matrix presentation[31] and the principle of interference of two coherent light beams,[32] a theoretical expression of the optical field distribution is obtained. Hence, via numerical simulation, optical field distributions are simulated to indicate the lithography results of different sample rotation mechanisms. In particular, by simulating multi-exposure with two kinds of laser at different wavelengths, we obtain unequal periodic 2D structures, i.e., a quasi-rectangular lattice and an irregular trapezoid lattice.
Figure
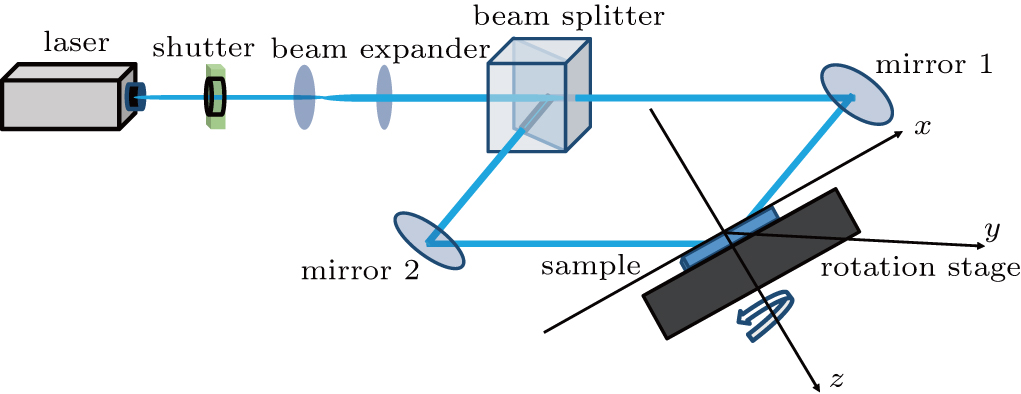 | Fig. 1. (color online) Schematic of lithography setup for micro-optical structure fabrication based on sample rotation and two-laser-beam interference. |
It can be assumed that the two coherent light beams that emerge from the beam splitter are plane waves and can be modeled as
 |
 |
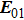
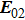
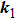
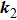
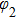
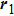
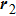
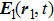
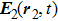
Assume that the sample is fixed on the x–y plane. Figure 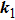



 |
 |
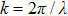
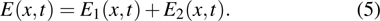 |
 | Fig. 2. (color online) Schematic of two-laser-beam interference on the sample surface, where 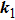

|
The irradiance of the electromagnetic wave is given by 
 |
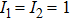
 |
 |
For a sample, two exposure methods are available. In one approach, N exposures are performed with 
 |
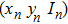
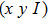
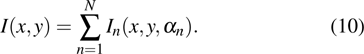 |
For the second exposure method, we assume that the angular velocity of the rotation is ω0; hence, the rotation angle can be expressed as a function of time, i.e., 
 |
If the total exposure time of the rotation process is T, the total optical field distribution can then be expressed as an integral
 |
Based on the equations obtained above, we employ a numerical simulation to obtain the field distribution for a given rotation/exposure configuration, so as to theoretically demonstrate the corresponding micro-optical structure that could be fabricated in practice. A standing wave optical field distribution is formed via the interference of two coherent lasers according to Eq. (
Although the optical field distribution obtained from two coherent lasers is 1D, by exposing the photoresist sample and applying different rotation methods, we can fabricate numerous 2D micro-optical structures. As noted above, one approach is to expose the sample N times with 
More interesting and complex structures can be fabricated by exposing and rotating the sample continuously. As an example, we simulate the total optical field distribution for the case in which the sample is continuously rotated with α = 180°, λ = 325 nm, and θ = 10°. An equally spaced concentric ring structure is obtained. Figure
As shown in Eq. (
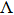
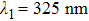



Furthermore, by exposing the sample four times with 45° sample rotations after each exposure (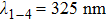
Various kinds of micro-optical structures can be fabricated using the proposed method, and the structure parameters can be controlled effectively by changing the laser-beam incidence angle and wavelength. The structures discussed above constitute selected examples of the various possibilities only.
We have proposed a method of fabricating micro-optical structures by employing sample rotation and two-laser-beam interference. By rotating and exposing a sample in different ways using the suggested interference device, a wide variety of micro-optical structures can be fabricated, such as hexagons and equally spaced concentric rings. By exposing the sample to lasers with different wavelengths, some irregular periodic optical structures can also be obtained. It is hoped that the proposed lithography method can be used for the fabrication of different kinds of micro-optical structures. Further, the micro-structures simulated in this study can be applied to numerous micro-optics fields. For example, the 1D grating can be used as a diffraction grating, the periodic hexagonal structure can be employed as a photonic crystal, and the spaced concentric rings can be used as a zone plate. Hence, the proposed technology will have considerable applications in the fields of micro- and nano-optics, because of its simple operation, low cost, and high output.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |





