† Corresponding author. E-mail:
At present, many chaos-based image encryption algorithms have proved to be unsafe, few encryption schemes permute the plain images as three-dimensional (3D) bit matrices, and thus bits cannot move to any position, the movement range of bits are limited, and based on them, in this paper we present a novel image encryption algorithm based on 3D Brownian motion and chaotic systems. The architecture of confusion and diffusion is adopted. Firstly, the plain image is converted into a 3D bit matrix and split into sub blocks. Secondly, block confusion based on 3D Brownian motion (BCB3DBM) is proposed to permute the position of the bits within the sub blocks, and the direction of particle movement is generated by logistic-tent system (LTS). Furthermore, block confusion based on position sequence group (BCBPSG) is introduced, a four-order memristive chaotic system is utilized to give random chaotic sequences, and the chaotic sequences are sorted and a position sequence group is chosen based on the plain image, then the sub blocks are confused. The proposed confusion strategy can change the positions of the bits and modify their weights, and effectively improve the statistical performance of the algorithm. Finally, a pixel level confusion is employed to enhance the encryption effect. The initial values and parameters of chaotic systems are produced by the SHA 256 hash function of the plain image. Simulation results and security analyses illustrate that our algorithm has excellent encryption performance in terms of security and speed.
With the wide development of internet technology and social networking services (SNS), more and more digital images, videos are transmitted and stored online, therefore the security of multimedium data has received much attention. Image encryption is an effective method to secure the digital images. Traditional encryption schemes, for example, data encryption standard (DES), advanced encryption standard (AES) and Ron Rives Adi Shamir Leonard Adleman (RSA) are not employed to effectively encrypt images because of the intrinsic features of the images, such as high correlation between adjacent pixels, bulk data capacity and high redundancy. Chaotic systems are characterized by sensitivity to initial conditions and parameters, ergodicity, pseudo randomness and topological transitivity, thus they are very suitable for image encryption.[1–3]
Since Matthews presented the first chaos-based encryption algorithm in 1989,[4] many chaos-based image encryption methods have been introduced.[4–10] For example, a fast image encryption algorithm based on only blocks in cipher text was given in Ref. [5], and Logistic map and skew tent map were used for constructing chaotic sequences. Zhou et al. [6] introduced a general chaotic framework named as cascade chaotic system (CCS), generated many new chaotic maps by using two one-dimensional (1D) chaotic maps as seed maps based on this framework, these newly generated chaotic maps have more unpredictable and better chaotic performance, and they have been applied to image encryption. Ye[7] presented a block-based image encryption algorithm by using wave function and chaotic system, and the random sequence produced by Chen chaotic system was employed to obtain the source point in the wave and give a diffusion matrix for modular operation. Recently, a novel chaos-based image encryption scheme based on compressive sensing was introduced,[8] and one-dimensional skew tent map was used to generate the measurement matrix. In view of the secure problems of low-dimensional chaos in image encryption and cycle degradation caused by computer finite precision, Zhang and Wang[9] put forward a novel image encryption algorithm by using a mixed linear-nonlinear coupled map lattice, and Tong et al. [10] designed a perturbed high-dimensional chaos according to Devaney and topological conjugate definition, and employed it for image encryption as pseudo-random sequence generators.
However, a number of encryption algorithms have illustrated security problems and proved to be unsafe.[11–25] In 2000, an efficient hierarchical chaotic image encryption (HCIE) algorithm was presented,[11] and it divided the plain image into blocks with the same size, and then operated position permutation at intra-block and inter-block levels. Recently, this algorithm has been cracked, and the security of HCIE against ciphertext-only attack is much lower, and it should be combined with confusion to provide high security.[12] Li et al. [13] gave a novel double-image encryption scheme by using chaos-based local pixel scrambling technique in gyrator transform (GT) domains, and Chen et al. [14] found that there is serious cross-talk disturbance in the decrypted phase-based image when the cipher image undergoes noise perturbation or occlusion attack. Liu et al. [15] evaluated the security of the encryption algorithm in Ref. [16], and found that it can be broken with only two pairs of known plain image and corresponding cipher images, pointing out that it has some security issues, such as insensitivity to the change of the plain image and secret keys. Zhang and Liu[17] proposed a novel image encryption method by using the permutation-diffusion architecture and skew tent chaotic map. Wang and He[18] found that this method had two flaws including that the key was fixed regardless of the plain image, and the permutation vector was constant for different original images, and it was vulnerable for chosen plaintext attack. Subsequently Eslami and Bakhshandeh[19] gave an improved method based on Ref. [17], and recently Akhavan et al. [20] cryptanalyzed this improved algorithm by using differential attack and found that it was not sensitive enough to the plain image. Recently, Wang et al. [21] analyzed a parallel sub-image encryption scheme combined with high-dimensional chaotic system in Ref. [22], and found that the produced keystream was unchanged for different original images, and the plain image may be recovered through chosen-plaintext attack. Li et al. [23] reevaluated the security of a novel image encryption algorithm in Ref. [24] and found that the scheme can be broken with only two known plain images, and they also cryptanalyzed the Fridrich’s chaotic image encryption scheme.[25] By analyzing these papers, the main flaw is that these encryption schemes have not enough sensitivity to the plain image, “one original image, one secret key” cannot be achieved, and they have less resistance to chosen-plaintext and known-plaintext attacks. Therefore, more secure and efficient image encryption methods are needed to be introduced and employed in secure communication field.
The classical encryption process consisting of confusion and diffusion was first introduced by Shannon,[26] and afterwards many image encryption schemes were designed based on it.[1,2,4–8,27–41] There are two methods employed in the confusion process. One is pixel level permutation[27–29] and the other is bit level confusion.[30–32] The former can change the positions of image pixels while the values of pixels are unchanged, and the latter can not only permute the positions of pixels, but also modify the values of the image pixels. Thus, bit level confusion is considered to be a perfect permutation method for the better encryption efficiency,[33] and a great many of image encryption schemes using bit level permutation have been introduced. For example, a new permutation method to confuse and diffuse the grayscale image at the bit level was proposed in Ref. [34], Arnold cat map was used to permute the bits, and logistic map was adopted for diffusing the permuted image. In view of the limits of Arnold cat map, it requires that the image must be square. Besides, logistic map has a dense set of periodic windows for a certain range of parameters, which restricts its application in image encryption. To alleviate the problem, Liu and Wang[35] presented a color image encryption method using bit-level permutation and high-dimensional chaotic system. Firstly, a color image (M × N) was converted into a grayscale image (M × 3N) through R, G, B splitting, and next a binary matrix was obtained by bit plane decomposition; secondly chaotic sequence generated from piecewise linear chaotic map (PWLCM) was employed to permute the two-dimensional (2D) bit matrix; thirdly, Chen’s chaotic system was used for diffusion. Recently, Martin et al. [36] gave a color image encryption algorithm based on three-dimensional (3D) cellular automata and chaotic maps, and 24 2D bit planes could be obtained from the bit plane decomposition of the color image, the 2D Cat map was used to permute the positions in each bit plane, and 3D cellular automata was employed for diffusion. In the bit level permutation process, after bit plane expansion of the original image, the 2D image is converted into a 3D bit matrix (the width, height and bit length), and each bit plane has its own weight. A majority of bit level confusion algorithms were manipulated on the 2D bit planes,[37–40] they decomposed the plain image into many bit planes. The confusion process of the plain image was transformed into that of the bit plane, more bit planes arose and more confusion steps were done. Moreover, some scholars have presented heterogeneous bit level confusion methods in view of the different importance of bit planes.[41] But in the final analysis, it was the confusion scheme of the 2D matrix or 1D vector from the 2D matrix. Few image encryption schemes confuse the original image as a 3D bit matrix, and thus bits cannot move to any position and any bit plane and the movement range of bits are limited. Thus, we may consider the original image as a 3D bit matrix, and then study the method to make the bit elements randomly move to any position in the matrix, thereby enhancing the permutation effect and upgrading the security level of the encryption scheme.
Based on the above analyses, a new image encryption algorithm using 3D Brownian motion and chaotic systems is introduced in the paper. Brownian motion is a random movement form of particles, generally existing in the liquid and gas, particles move fast in the 3D space, and the movement traces distribute in the whole space. Our contributions are as follows: first, we employ the 3D Brownian motion to confuse the bits in the 3D bit matrix, where the bits are regarded as Brownian motion particles, and use the Monte Carlo method to simulate Brownian motion. Due to the increase of the image size, the 3D bit matrix is split into many sub blocks to save the execution time, a new block confusion based on 3D Brownian motion (BCB3DBM) is given to confuse the positions of the bits within the blocks, and logistic-tent system (LTS) is employed to generate the direction of particle movement. Besides, block confusion based on position sequence group (BCBPSG) is introduced to confuse the positions of the sub blocks, random chaotic sequences are produced by a four-order memristive chaotic system and sorted, a proper position sequence group is picked out according to the plain image and utilized to change the position of the sub block. Our confusion method can fully change the positions of the bits and their weights, the bits in one bit plane can appear at any position and in any bit plane theoretically, and it greatly increases the encryption performance. Furthermore, diffusion is adopted to increase the security of the algorithm. In order to improve the algorithm sensitivity to the plain image and the ability to resist the known-plaintext and chosen-plaintext attacks, the initial values and parameters of chaotic systems are obtained by the SHA 256 hash value of the original image.
The rest of the present paper is organized as follows. In Section
The concept of memristor was initially presented by Chua in 1971,[42] it is believed to be the fourth passive circuit element, and other three elements are resistor, capacitor and inductor. In recent years, the studies of memristor-based dynamical systems have been receiving more and more attention because of their potential applications in signal processing, neural networks, image encryption and other fields.[43–45] The memristive chaotic systems have complex dynamical characteristics and close dependence on the initial values and system parameters, and they are desirable for image encryption.
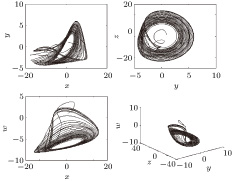
Chua’s diode with Chua’s circuit was replaced with an active memristive circuit, and it was composed of a negative conductance and a flux-controlled memrisor, therefore a novel four-order memristive system was presented,[46] and it can be derived as follows:
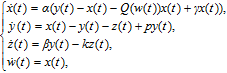 | (1) |
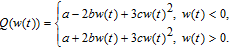 | (2) |
And when α = 9, β = 13, γ = 2, p = 0.003, a = 0.8, b = – 0.03, c = 0.01, and k = 0.05, the system is chaotic with a positive Lyapunov exponent LE = 0.185, and its attractor diagram is shown in Fig.
Utilizing the logistic map and tent map as seed maps, LTS is presented in the following equation[47]
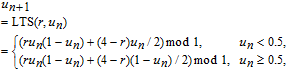 | (3) |
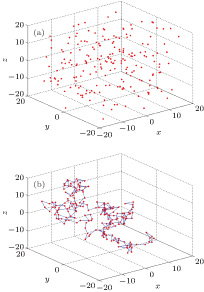
Brownian motion is a random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collisions with the fast-moving atoms or molecules in the gas or liquid. A point in the space may be shown in Fig.
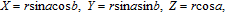 | (4) |
One point in the space is regarded as one Brownian particle. When the direction of movement and step length are given, the position of Brownian particle can be determined. Here, the step length is chosen as r = 2, the random number generator function is employed to calculate the direction of movement, then the x, y, z components of the position of each Brownian particle can be obtained. Brownian motion can be simulated through Monte Carlo method. We simulate the Brownian motion of 200 particles in the 3D space, a matrix of 200 × 3 is utilized to store the positions of Brownian particles, and the x, y, z components are limited in a region of [–20, 20]. Figure
In the proposed algorithm, SHA 256 hash function is used to generate the initial values and control parameters of the chaotic systems. Before encrypting the plain image, its SHA 256 hash value is computed as the 256-bit secret key K, and it can be denoted by
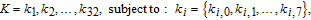 | (5) |
In the encryption process, two LTSs are employed to determine the direction of Brownian particle movement, and another two LTSs are required in the confusion process to modify the pixel values of the plain image. Thus, four initial values and four parameters for LTSs are derived as follows:
 | (6) |
In addition, the initial values for the memristive chaotic system can be computed by
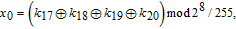 | (7) |
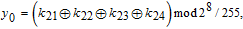 | (8) |
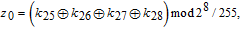 | (9) |
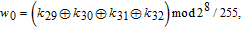 | (10) |
According to Eqs. (
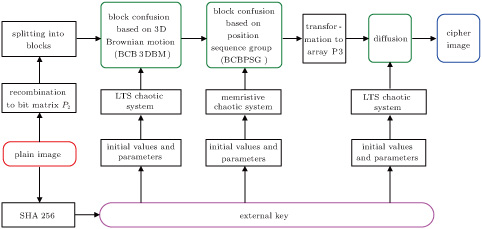
In order to improve the encryption speed, the confusion process of the plain image is manipulated by block. Our confusion strategy consists of block confusion based on 3D Brownian motion (BCB3DBM) and block confusion based on position sequence group (BCBPSG).
Firstly, by splitting the bit planes, the plain image P with a size of M × N is converted into a 3D bit matrix P 1 with the size M × N × 8, and the width r 1, the height r 2 and the bit length r 3 are M, N, and 8, respectively. Secondly, transforming the bit matrix P 1 into a cubic matrix P 2, the sizes are all r, and r 3 = M × N × 8. For example, when M = N = 512, then the size of the cubic matrix is 128 × 128 × 128. The transformation of a 3D bit matrix into a cubic matrix may reduce the iterative times of memristive chaotic systems and save the permutation time. Secondly, splitting the cubic matrix P 2 into many 3D sub blocks, the size of every sub block is m × m × m, and there are n 3 blocks (n = r/m). Then, we use Brownian motion to permute the positions of the bits for each sub block.
If the 3D bit matrix of the original image cannot be transformed directly into a cubic matrix, a cubic matrix may be obtained through adding more pixels to the plain image.
Block confusion based on 3D Brownian motion (BCB3DBM) is employed to confuse the positions of bits within each sub block. The detailed steps are as follows.
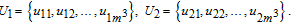 | (11) |
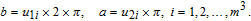 | (12) |
When they move to the same location, in other words, the final locations of the Brownian motion particles are the same, the former particle (named particle 1) in the 3D matrix moves to this place, the latter particle (named particle 2) is picked out, and when the movements of other particles have finished, the particle 2 moves to the empty position in 3D bit matrix. When particle 2 represents more particles than one, they are shifted to the empty positions according to the order of sequence in the 3D matrix.
After BCB3DBM is applied to each sub block, the sub block image is regarded as a unit, its position is permutated based on position sequence group. The detailed steps of block confusion based on position sequence group (BCBPSG) are shown below.
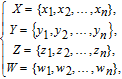 | (13) |
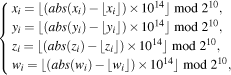 | (14) |
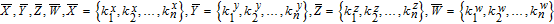

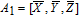
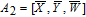
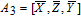
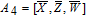
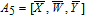
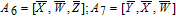
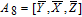
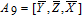
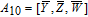
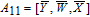

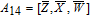

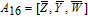
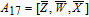
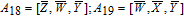
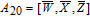
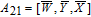
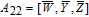
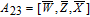
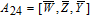
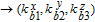
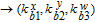
As is well known, there are different bit weights at different bit planes. Through BCB3DBM and BCBPSG, each bit is moved to other bit planes and its weight is also changed. That is to say, the position and weight of any bit are changed simultaneously, and therefore our confusion scheme has a good diffusion effect. Besides, in BCBPSG, 24 different position sequence groups are produced, a proper group depending on the plain image is chosen to confuse the sub blocks. Therefore, the confusion process has strong sensitivity to the plain image, and our algorithm has higher security level.
Diffusion is performed at the pixel level. Firstly, the confused bit matrix is transformed into a 2D pixel matrix, which is subsequently resized to a 1D pixel array P 3(1 × MN). Secondly, iterate the LTS using the initial values and parameters u 30, r 30, u 40, and r 30, sequences U 3, U 4, and U are obtained by the following equation:
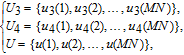 | (15) |
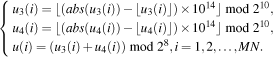 | (16) |
Next, perform diffusion by Eqs. (
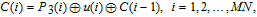 | (17) |
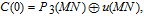 | (18) |
As shown in
The proposed encryption scheme has the following merits.
Firstly, SHA 256 hash function of the plain image is employed to generate the secret key, a four-order memristive chaotic system and LTS are used to produce the chaotic sequences for confusion and diffusion, initial values and parameters of the chaotic systems are obtained from the secret key, and therefore the encryption algorithm is highly sensitive to the plain image and it can withstand chosen-plaintext and known-plaintext attacks.
Secondly, we adopt the encryption architecture of confusion and diffusion. The confusion strategy is composed of block confusion based on 3D Brownian motion (BCB3DBM) and block confusion based on position sequence group (BCBPSG). Before encryption, the plain image is transformed into a 3D bit matrix through bit plane decomposition. In order to improve encryption speed, the 3D bit matrix is divided into many non-overlapping sub blocks, strongly random 3D Brownian motion is used to confuse the position of the bits for the first time, Monte Carlo method is used to simulate Brownian motion, and bit elements are regarded as Brownian motion particles.
Thirdly, the subsequent BCBPSG is used to confuse the position of the sub blocks based on position sequence groups generated by a four-order memristive chaotic system, and the confusion process is controlled by the plain image. Thus, the proposed confusion method can attain the permutation of inter and intra sub blocks, which makes the bits in one bit plane shift to any position and any bit plane in theory, so it has good confusion effect.
Finally, in order to upgrade the encryption effect, the diffusion step atpixel level is performed on the confused image, the LTS is used to produce the key sequences, and we obtain the cipher through manipulating the XOR operation on the current image pixel, previous cipher pixel and key sequence element.
In this section, several experiments are conducted on multiple images, Lena, Baboon and Peppers of size 512 × 512 are chosen as the original images, and all the experiments are performed on a personal computer with the following hardware environment: 2.5-GHz CPU, 4-GB memory, and Windows 7 operating system, and the compiler software is Matlab 2014a. Some keys we use here are as follows: α = 9, β = 13, γ = 2, p = 0.003, a = 0.8, b = −0.03, c = 0.01, and k = 0.05, the Brownian movement rounds R = 100, the size of every sub block image of 8 × 8 × 8 and the iterating parameter of the memristive chaotic system, l = 500. Figures
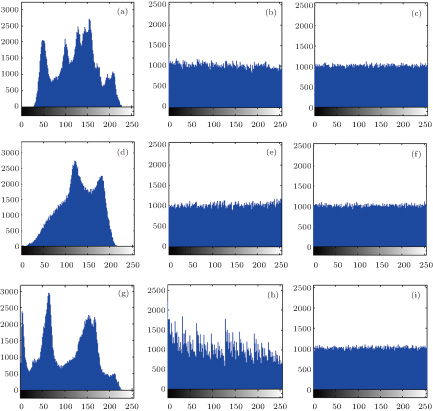
From the results, we can conclude that the confused images and cipher images are similar to noise images, any useful information cannot be obtained from them, and thus the proposed encryption algorithm has a good encryption effect and it can be applied to the secure transmission of private information.
A good encryption algorithm should have a large enough key space to make the brute force attacks infeasible. In our algorithms, the secure key includes (i) the 256-bit long SHA 256 hash value; (ii) the Brownian movement rounds R; (iii) iterating parameter l of the memristive chaotic system; (iv) the first pixel value P(1) of the plain image. It is known that the key space of SHA 256 with complexity of the best attack is 2128 larger than 2100,[48] which means that our algorithm is enough to resist any brute force attack.
The histogram is used to reflect the distribution of the pixels. The uniform distribution can hide the information about the plain image. Figure
Besides, variances of histograms are used to quantitatively evaluate the uniformity of the images. When the variance is lower, and the uniformity of the image is higher. The variance of histograms can be obtained by the following equation:[9]
 | (19) |
| Table 1.
Variances of the histograms of the Lena (512 × 512). . |
Information entropy can be calculated from
 | (20) |
| Table 2.
Information entropies of the plain and cipher images. . |
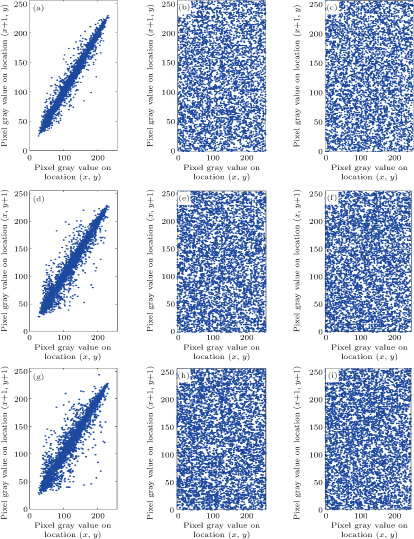
Adjacent pixels of the plain images have a strong correlation, which makes the leakage of the information possible. Thus, an effective image encryption algorithm should remove the correlation. 5000 pairs of pixels in horizontal, vertical and diagonal direction are randomly chosen from the plain, confused and cipher images and the coefficients are calculated as follows:
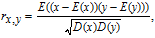 | (21) |
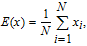 | (22) |
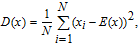 | (23) |
Figure
| Table 3.
Correlation coefficients of two adjacent pixels in the plain, confused and cipher images. . |
Number of pixels change rate (NPCR) and unified average changing intensity (UACI) are employed to assess the resisting differential attack performance of the proposed encryption algorithm. For two gray cipher images, the NPCR and UACI can be calculated from
 | (24) |
 | (25) |
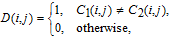 | (26) |
We use Lena as the plain image, choose a location (i, j), change its pixel value and obtain another plain image. The two plain images are encrypted by our algorithm, the corresponding cipher images are utilized to compute NPCR and UACI, and the results are listed in Table
| Table 4.
Lena images for different positions. . |
Next, six test images are selected, and a pixel from the plain image is randomly chosen and the pixel value is added by 1, then a new plain image appears. The new cipher image and the old cipher image are employed to calculate the NPCR and UACI values. The 100 random pixels are selected for each image. The average, minimum, maximum NPCR and UACI values are shown in Table
| Table 5.
NPCRs and UACIs between ciphers while plain images only have one different pixel. . |
Key sensitivity of an image encryption algorithm can be assessed in two ways: (i) when the plain image is the same and the key has a slight change, a completely different cipher image should be obtained; (ii) the plain images cannot be recovered even though there is a slight difference between the encryption key and decryption key. Next, we will test the performance of our algorithm from these two aspects.
Firstly, Lena (Fig.
 | Fig. 9. (color online) Encryption results with the key changed, showing (a) cipher image with K1
, (b) difference between two cipher images, and (c) the histogram of Fig. |
Secondly, we use a different decryption key to decrypt the cipher image shown in Fig.
 | Fig. 10. Decryption results with different keys, showing (a) recovered image with K, (b) recovered image with K
1, and (c) subtraction of Fig. |
From the above analyses, it is clear that the proposed algorithm is highly sensitive to the secret key and the plain image, and it is secure to withstand statistical attack and brute force attack.
Occlusion attack means that the cipher image is damaged in the transmission process, and the more data it loses, the more distortion the recovered image has. The peak signal-to-noise ratio (PSNR) is employed to calculate the quality of the recovered image after being attacked. For a grayscale image, the PSNR may be expressed as
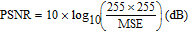 | (27) |
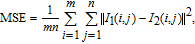 | (28) |
The results are shown in Fig.
| Table 6.
Quantitative results of resisting occlusion attack. . |
In the image transmission, channel noise is inevitable. Gaussian white noises with zero mean and three different variances are added to the cipher image (Fig.
| Table 7.
Quantitative results of resisting noise attack. . |
Many encryption schemes are broken by known-plaintext and chosen-plaintext attacks. In the present paper, two methods are manipulated to upgrade the ability to resist known-plaintext and chosen-plaintext attacks. On the one hand, the chaotic sequences used in confusion and diffusion processes are generated from the four-order memristive chaotic system and LTS, the initial values and parameters of the chaotic systems are calculated by SHA 256 hash value of the plain image, and thus our algorithm depends on the original image. On the other hand, 24 different position sequence groups are obtained in BCBPSG, a certain group is picked out to confuse the sub blocks, and its choosing method has high relationship with the plain image. Therefore, in theory, our encryption algorithm has strong ability to withstand the known-plaintext and chosen-plaintext attacks.
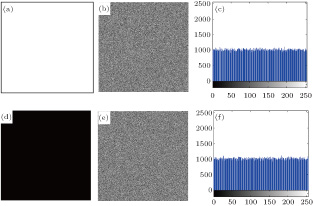
The cryptanalysts often choose special images, such as all black and all white to attack the cryptosystem. They want to obtain the key by analyzing the cipher images. Figure
| Table 8.
Entropies and correlation coefficients of the plain, cipher images of all white and all black. . |
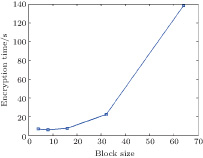
Speed is an important issue for a cryptosystem. The proposed encryption scheme consists of block confusion based on 3D Brownian motion (BCB3DBM), block confusion based on position sequence group (BCBPSG) and diffusion. Before the confusion process, the original image is transformed into a 3D cubic matrix, the aim is to reduce the iterative times of memristive chaotic systems and improve the encryption speed. In addition, the cubic matrix is divided into many sub blocks. The permutation process is manipulated by blocks, and it can run in parallel, thereby saving time. The size of the sub block image and the test image can affect the encryption speed. For a 512 × 512 gray image, the encryption times for 4 × 4 × 4, 8 × 8 × 8, 16 × 16 × 16, 32 × 32 × 32, 64 × 64 × 64 blocks are tested, and the relationship between execution time and the size m of the sub block image is shown in Fig.
A novel chaos-based image encryption algorithm using the three-dimensional (3D) Brownian motion is given in this paper. We present the block confusion based on 3D Brownian motion (BCB3DBM) and block confusion based on position sequence group (BCBPSG). The BCB3DBM is used to confuse the position of the bits within the plain-image sub blocks, and the subsequent BCBPSG is employed to permutate the positions of the sub blocks. In theory, the permutation process can make the bits in one bit plane appear at any position and in any bit plane, and our confusion scheme has a good scrambling result. Moreover, we also utilize confusion to enhance the encryption effect. In the encryption scheme, the four-order memristive chaotic system and LTS are used to generate the chaotic sequences. Besides, SHA 256 hash function of the plain image is employed to produce the initial values and parameters of the chaotic systems, and therefore our encryption scheme has strong sensitivity to the plain image.
In the security analyses, we employ 10 different methods, i.e., key space analysis, histogram analysis, information entropy analysis, correlations between two adjacent pixels, and resistance to differential attacks, key sensitivity analysis, resisting occlusion attack analysis, resisting noise attack analysis, resisting known-plaintext and chosen-plaintext attack analysis and speed analysis to assess the performance of this algorithm. The experiment results show that our method is secure and effective. It has potential applications in multimedia communication.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] |