Cite this Article
Wang Lei, Zheng Jie-Hui, Zhang Xiao-Shuang, Zhang Jian-Lin, Wang Qiu-Zhen, Zhang Qian. Pedestrians’ behavior in emergency evacuation: Modeling and simulation. Chinese Physics B, 2016, 25(11): 118901  
Permissions
Pedestrians’ behavior in emergency evacuation: Modeling and simulation
Wang Lei, Zheng Jie-Hui, Zhang Xiao-Shuang, Zhang Jian-Lin, Wang Qiu-Zhen†, , Zhang Qian
School of Management, Zhejiang University, Hangzhou 310058, China

 

† Corresponding author. E-mail: wqz@zju.edu.cn

Project supported by the National Natural Science Foundation of China (Grant No. 71471163).

Abstract
Abstract

The social force model has been widely used to simulate pedestrian evacuation by analyzing attractive, repulsive, driving, and fluctuating forces among pedestrians. Many researchers have improved its limitations in simulating behaviors of large-scale population. This study modifies the well-accepted social force model by considering the impacts of interaction among companions and further develops a comprehensive model by combining that with a multi-exit utility function. Then numerical simulations of evacuations based on the comprehensive model are implemented in the waiting hall of the Wulin Square Subway Station in Hangzhou, China. The results provide safety thresholds of pedestrian density and panic levels in different operation situations. In spite of the operation situation and the panic level, a larger friend-group size results in lower evacuation efficiency. Our study makes important contributions to building a comprehensive multi-exit social force model and to applying it to actual scenarios, which produces data to facilitate decision making in contingency plans and emergency treatment.

PACS: 89.65.Gh;89.40.–a;07.05.Tp;05.65.+b
Keyword:multiple exits;social force model;interpersonal affect;panic
1. Introduction

Emergency management is an important social issue about people’s safety and wellbeing. The primary thing is to evacuate the people involved efficiently when an emergency occurs. Given the importance and complicacy of evacuation, it is critical to complement existing theoretical and practical approaches to ensure a smooth evacuation.

Most studies use modeling and programming to simulate pedestrians’ behavior when emergencies occur. Pedestrian simulation models in the existing literature can be categorized into two categories: discrete model and continuous model. The majority of discrete models are based on cellular automata models, with space and time discrete during the evacuation while the continuous models simulate everyone’s position at every second in succession. The fluid-dynamic model,[1–3] cost function model,[4,5] and social force model[1,6,7] are certain examples of continuous models. The social force model that considers the physical force of the environment and introduces the socio-psychological force has been widely used by researchers.

Lu et al.[8] developed an extended floor field cellular automaton model to test the influence of walking behaviors of pedestrian groups on pedestrian flow dynamics in reality, which needs five basic rules to support. You et al.[9] gave a calculation method of the probability of the pedestrian movement by using a three-dimensional cellular automata evacuation model with dynamic variation of the exit. Li et al.[10] found that heterogeneous behavioral tendencies in humans, that is, familiarity and aggressiveness, impacted the evacuation time by an extended cellular automata model. Although much research has advanced the simulation progress of pedestrians’ evaluation with discrete models, we find that a discrete model must establish a series of rules to meet the discrete requirement for time and space, which makes pedestrian behavior simulations not as accurate as a continuous model since it could simulate the behaviors of pedestrians more vividly. Therefore, the social force model is preferred in this study.

With the development of research on pedestrian evacuation, more and more researchers have improved the social force model and applied it to practice. Li et al.[11] developed a four-stage transfer model and noted that the congestion risk was higher in transfer aisles than on escalators. Yang et al.[12] built a social force model involving the factor of guidance to simulate the evacuation issues in the Beijing South Railway Station and found that the guidance enhanced evacuation efficiency. Wang et al.[13] introduced friendship attraction and attractive forces of an exit into the initial social force model and simulated the pedestrian flow in a station hall during the Chinese spring festival. Jiang et al.[14] found the optimal design of architectural entities based on social force. Yang et al.[15] explored the pedestrian evacuation under fire in a subway station on the foundation of the social force model, using the software FDS + Evac.

In addition, lots of factors, which affect the evacuation efficiency, have also been discussed in the existing literature. The attributes of exits, such as the height and the width, have large impacts on the progress of an evacuation. Wei et al.[16] modified the static floor field model and conducted a regression analysis to explore the relationship between the reference point and the exit width. Lin et al.[17] proposed a granular dynamic model on the basis of the discrete element method, to simulate the characteristics of crowd flow through an exit. They also suggested exploring multi-exit evacuation in future studies. However, multi-exit choice may be the most difficult and complex aspect of an actual scenario. There are few studies discussing individual decisions regarding multiple exits, particularly in terms of combining a continuous model with a multi-exit model.[18] In addition, not only physical factors but also psychological factors exhibit large impacts on evacuation efficiency. Moussaid et al.[19] analyzed the crowd dynamics by building an individual escape model and found that social interactions among group members significantly influenced crowd dynamics. Hu et al.[18] proposed a novel three-dimensional cellular automata model to simulate evacuation from a lecture theatre and found that a larger group size resulted in longer evacuation time. Though behavioral models have been used to describe features of pedestrian flow in normal operation situations,[11,12,16,18,19] few studies analyze the interaction among friends when an emergency occurs.

Based on evacuations under multi-exit scenarios in reality, this paper aims to propose a comprehensive model by combining the behavioral model with a multi-exit utility function. We develop a model based on the modified social force model indicated in our previous work.[13] In this paper, significant improvements include the following four aspects: (i) visual range and relative friend attractiveness of the corresponding velocity are incorporated into the social force model; (ii) a multi-exit choice mechanism is added into the advanced model; (iii) the congestion effect and design of exits are taken into account; (iv) the emergency case is discussed and the difference between different levels of panic is compared. By considering all these aspects, a series of computer simulation experiments are conducted to further quantify the impact of these factors on pedestrian evacuation.

In order to explore individual decision mechanisms under multi-exit conditions and identify the factors that affect evacuation efficiency, the comprehensive model and initial processing of the simulation of evacuation in Wulin Square Subway Station in Hangzhou are presented in the next section. Then we program to modify the simulation of a pedestrian crowd in the subway station waiting hall to determine how the pedestrian density, panic level and friend-group size affect evacuation efficiency in both normal operation cases and emergency cases in Section 3. Finally, we conclude the limitations and future research avenues of our study in Section 4.

2. Methods
2.1. Modified social force model
2.1.1. Visual range

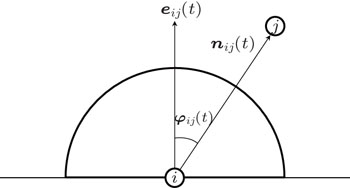
The initial social force model does not consider the effect of visual range on the psychological force. Something within one’s visual range can easily draw one’s attention. In terms of the pedestrians’ psychological characteristics, we define the visual range as the 90 degrees to the left and to the right of pedestrian i’s moving direction where φi j(t) in Fig. 1 is the angle between individual i’s moving direction ei j(t) and normal vector ni j(t) pointing from individual i to individual j. Thus,

If cos(φi j(t)) ≥ 0, we consider the psychological force of pedestrian j on pedestrian i; otherwise, we ignore it.

Fig. 1. Visual range of pedestrian i.

In conclusion, we define

and modify the psychological force as follows:

where Ai is a positive constant representing the repulsive force strength, Bi is a distance factor measuring the role of distance on the repulsive force, rij is the sum of the radius of an area covered by pedestrians i and j respectively, dij denotes the distance between the center of mass of pedestrian i and that of pedestrian j, and ni j denotes the distance vector pointing from pedestrian j to i.

2.1.2. Attraction and relative speed to companions

Although many studies have already considered interactions among pedestrians, they have seldom considered relative speed. Thus, we consider the relative speed and define the following expression:

where c donates the influence coefficient of relative velocity; is the normal relative velocity of individual i to his friend q as shown in Fig. 2; the parameter Ti is a negative constant reflecting attractive force from friend q to pedestrian i; riq denotes the sum of the radii of an area covered by pedestrian i and his friend q respectively; diq denotes the distance between the centers of mass of i and that of q; Fi is a distance factor measuring the role of the distance on the attractive force from the friend and niq denotes the distance vector pointing from q to i.

Fig. 2. The clarification of normal () and tangential () relative velocity.
2.1.3. Modified social force model

To consider the visual range, we modify the initial social force model as follows:

where fij is the integrated force between individual i and another pedestrian j; is the repulsive force describing the attempts of individual i to maintain a safe distance from pedestrian j; denotes the friction of physical interactions between individual i and pedestrian j; k donates the contact force strength factor and κ is the coefficient of friction; is the tangential relative velocity of individual i to pedestrian j; the function g(x) is defined by

that is, when there is no contact among pedestrians, the g(x) equals 0, and ti j denotes the tangential vector pointing from pedestrian j to i.

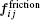
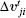
The interaction between individuals and walls or obstacles is computed analogously using the psychological force, repulsive force and friction force. The corresponding expression is as follows:

The attraction of an exit, portraying pedestrian i’s intention to move towards the exit K, is computed in the same manner as the psychological force

where Ci is a negative constant representing the attractive force strength from exits, Di is a distance factor measuring the role of distance on the attractive force from exits, and nik denotes the distance vector pointing from exit k to i.

Finally, the desired velocity is modified by adding a panic parameter[13]

where p represents pedestrians’ panic level and it ranges from 0 to 1, is the value of the desired velocity, donates a unit vector along the moving direction of pedestrians and v̄i donates the average velocity perceived from all the other pedestrians around the individual i within an area, the radius of which is 2–3 m.[20] When p equals to 0, which means that there exists no emergency, pedestrians are evacuated regularly according to their own desired velocity. When p equals to 1, which means that there is full panic, pedestrians are more scared and more easily affected by others, that is to say, the velocity of a pedestrian totally depends on the velocity of other pedestrians around him in cases of panic.

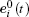
In conclusion, we extend the acceleration equation as follows:

where τi represents response time and ɛ is a random error referring to the slight deviation from the average moving direction.

2.2. Evacuation decision under multiple exits
2.2.1. Design of an exit

Previous research indicated that the width of an exit influenced the attraction of the exit significantly, that is, a wider exit would exert a greater attractive force on pedestrians.[21] In addition, the height of an exit is also a factor considered in our study. Thus, we apply the dynamic floor field model to compute the effect of the height and width of the exit

where deUk denotes the utility of exit k’s design; wkw denotes the weight of the width effect; kw is a sensitive degree coefficient indicating the pedestrian’s perception of the exit’s width; and W is the width of the exit. In addition, wkh denotes the weight of the height effect, and wkw + wkh = 1; kh is a sensitive degree coefficient indicating the pedestrian’s perception of the exit’s height; and H is the height.

2.2.2. Congestion effect

Congestion occurs when people gather toward an exit. The physiological features and behaviors of a congested crowd affect the outcome of an evacuation apparently.[22] The following advanced model proposed by Zainuddin and Shuaib is used to describe the utility of the effect of the distance between individual i and exit k:[23]

The distance between individual i and exit k can be divided into two parts: the uncongested distance diuk and the congested distance rk, which is the radius of the semicircle area. According to Eq. (10), li is a positive constant measuring the individuals’ variances when they assess distance factors; Ei(t) donates the excitement factor of individual i at time t; αi ∈ [0,1] measures the individuals’ maximum repulsive effect; βi donates a constant radius–repulsion relation factor perceived by individual i; rmax is the maximum radius among all congested areas at the exits; and δ (φik(t)) measures the perception of the individual i of the exit k regarding his excitement. The parameters above are defined according to Ref. [23]. Readers can refer to it for more details.

Under multi-exit circumstances, the exit choice depends on the individual’s perception of congestion. If the preceding exit is too crowded to escape, a pedestrian must change his current direction. Helbing[22] and Senevarante[24] noted that a pedestrian would head for a new exit if the utility difference between the new exit and the current exit was larger than the threshold. In this manner, the multi-exit choice function DSchange,i is as follows:

where gi denotes the threshold utility when individual i changes his current exit, which is determined by the excitement factor and the pedestrian’s mental characteristics; ecurr,i denotes the current exit in his direction; enew,i denotes the new exit which he changes to; Ucurr,i denotes the utility when he chooses the current exit; Ubest,i denotes the maximum utility among the available exits; and DSchange,i denotes the decision function.

2.2.3. Evacuation decision under multiple exits

Combining the above functions, we can obtain the multi-exit choice utility function as follows:

The best_exit(t) represents the current optimal exit; Uik(t) denotes the utility of exit k to individual i; deUk denotes exit k’s utility of design; diUik(t) denotes the utility of the distance between individual i and exit k.

2.3. Multi-exit social force model

Finally, we create a modified model of the multi-exit social force model as the combination of Eqs. (8), (13), and (14). It shows as follows:

Social force model:

Multi-exit choice model:

2.4. Initial processing of simulation study

This study chooses the passenger evacuation hall of the Wulin Square Station, which is the largest subway station in Hangzhou, China, as a basic research background. Given the hall (Fig. 3) with the length of 77.6 m and the width of 17 m, which also has two exits (B and E), we set that area as the simulation area. In the initial condition, pedestrians were randomly positioned in the waiting room before they were evacuated through the two exits with the same probability. No matter what the condition is, the primary purpose of those pedestrians is to get out of this hall as soon as possible, especially when emergencies occur.

Fig. 3. Schematic diagram of the evacuation hall of Wulin Square Subway Station in Hangzhou, China.

According to the classical articles,[6,23] we adjust certain parameters, while it should be accepted that the calibration of these parameters needs more future work because of the shortage of experimental data. The key parameters of the present model are exhibited in Table 1.

Table 1.

Parameters of the modified social force model.

.
3. Results and discussion

Pedestrian flow simulations in the waiting room of the station hall were conducted under two different situations: the situation under normal operations, and the situation under an emergency (or congestion). Under normal operations, we considered the impacts of the pedestrian density and the friend-group size. When emergencies occurred, we took the friend-group size and different levels of panic into account.

There also exist two states no matter under what the operation case: typical state and holiday state. In the typical state, the number of passengers is rather different from that in the holiday state. We regarded less than 400 people in the hall (typical state) as low pedestrian density, while more than 600 people (holiday state) as high. We defined a high friend-group density for holiday states (the proportion of pedestrians in groups to total pedestrians was as high as 80%) but a low friend-group density for the typical state (the proportion was only 20%). Besides, according to Moussaid’s study, people always gathered 2 to 4 people in a small group when they hung out,[19] therefore, we set the size of friend-group ranging from 2 to 4.

3.1. Case I: Simulation of normal operations

In the typical state of normal operation situation, there are approximately 400 pedestrians in the waiting room. Thus, the total pedestrian flow is set to 400 with a regular speed of 1.5 m/s. No matter on workdays or in the holidays, parts of pedestrians hang out in groups. In this way, the pedestrians were partitioned into two parts: one part represents friend-group (green ones in Fig. 4) while the other part stands for single pedestrian (blue ones in Fig. 4). Specifically, the number of companions in one group represents the friend-group size. For example, two green ones form a small group which means that the friend-group size is 2. The simulation of a single trial in different time steps is shown in Fig. 4

Fig. 4. Case I: evacuation processes of a single trial at different time steps: (a) step = 0, (b) step = 150, (c) step = 200, and (d) step = 350. The initial number of pedestrians in the waiting hall is 400.

The self-organization phenomena can be clearly observed in the simulation process. As shown in Figs. 4(a) and 4(b), once the pedestrians surge, they flood to two exits spontaneously in two streams, thus forming a phenomenon called the automatic channelized phenomenon.[6,25] However, the pedestrians in the red circle change their route (from Exit B to Exit E, as shown in Figs. 4(b) and 4(c)) after evaluating the utility of the two exits. In addition, figure 5 reveals that the number of people evacuated from Exits B and E are similar at the early stage of the overall process; but the number of people evacuated from Exit E is larger than that from Exit B at the end. This result also reflects the pedestrians’ evacuation decisions are based on utility. Furthermore, in Fig. 4(d), the “arch” effect is created when pedestrians rush to Exit B.

Fig. 5. Number of pedestrians evacuated through different exits in one trial.

The phenomena that arose in the simulation process (e.g., self-organization phenomena and “arch” effect) were in line with those in the classical articles,[6,23] which proved that the modified model regarding these adjusted parameters is effective to some degree.

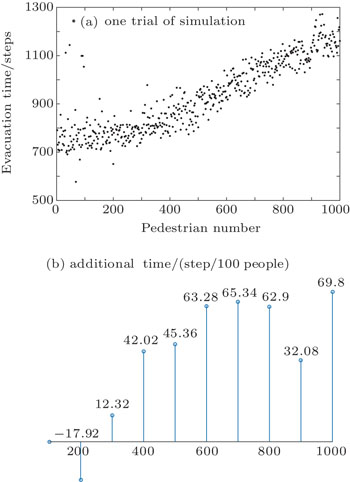
3.1.1. Simulation with different pedestrian flows

Evacuation efficiency is highly related to the pedestrian density (the number of passengers). The desired velocity will increase if pedestrian density is low.[19,26] We simulated the evacuation process with passenger numbers varying from 100 to 1000, set the normal speed to 1.5 m/s in each condition, performed each condition more than 50 repetitions, and obtained the additional average evacuation time (see Table 2).

Table 2.

Case I: evacuation time with different numbers of evacuated people.

.

The results in Fig. 6 indicate that the pedestrian density impacts the total number of people evacuated. When in the same time steps, less people are left in the hall in low pedestrian density. There is no difference in evacuation time for the number of pedestrians varying from 100 to 300, but with the number of pedestrians increasing from 400 to 1000, the evacuation time increases sharply (see Table 2 and Fig. 7). Besides, the evacuation time for every 100 pedestrians first decreases and then increases as the total number of pedestrians increases in the condition of low pedestrian density (typical state), reaching a minimum when the total number is approximately 200. Meanwhile, in the condition of high pedestrian density (holiday state), the evacuation time for every 100 pedestrians also first decreases and then increases as the total number of pedestrians increases, reaching a minimum when the total number is approximately 900. In a word, as for evacuating every additional 100 people, the most efficiency pedestrian density is approximately 200 in low pedestrian density (typical state) and 900 in high pedestrian density (holiday state).

Fig. 6. Case I: different evacuation processes of a single trial with different pedestrian densities: (a1)–(a4) high pedestrian density where the initial number of pedestrian is 800 and (b1)–(b4) low pedestrian density where the initial number of pedestrian is 300 at different time steps: (a1) and (b1) step = 0, (a2) and (b2) step = 200, (a3) and (b3) step = 400, and (a4) and (b4) step = 600. Here, Pin donates the number of pedestrians left in the waiting hall and Pout donates the number of pedestrians who have escaped from the waiting hall at the specific time step.
Fig. 7. Case I: evacuation time of fifty trials with different pedestrian densities. (a) Each dot represents one trial. Once there was an additional 100 pedestrians, 50 trials would be simulated in each condition. (b) The additional time to evacuate the first 100 pedestrians was 0. The other lines represent the additional average evacuation time for an additional 100 pedestrians compared with that in the previous stage. 200 pedestrians and 900 pedestrians in panel (b) represent the most efficient evacuation time in low and high pedestrian density respectively.

There is sufficient space for individuals to keep a certain distance from each other when the pedestrian density is low (or in the typical state: less than 400 people in the hall). With weak interaction among each other,[25] an individual’s behavior mainly depends on the individual himself. Thus, fewer constraints lead to lower efficiency. When pedestrian density increases,[25] the interaction force increases synchronously, but the mechanisms become increasingly complex, which may result in an un-organizational phenomenon or chaotic flow. When the pedestrian density reaches to high (or holiday state: more than 600 people in the hall), first the increasing interaction improves evacuation efficiency at the early stage while the efficiency decreases and then reaches a second optimal point in high pedestrian density when the number of pedestrians evacuated is 900. Therefore, we found the different thresholds of pedestrian density in typical state and holiday state respectively, which was of importance to emergency management.

3.1.2. Simulation with different friend-group sizes

The simulation results in the “low friend-group density” (or the typical state) and the “high friend-group density” (or the holiday state) are shown in Table 3 and Fig. 8. The evacuation efficiency in high friend-group density is lower than that in low friend-group density. For example, there are 370 people who have escaped in high friend-group density but 401 in low friend-group density at the time step of 600 (Fig. 8).

Fig. 8. Case I: different evacuation processes of one trial with different friend-group densities: (a1)–(a4) low friend-group density where the proportion of pedestrians in groups to total pedestrians is only 20% and (b1)–(b4) high friend-group density where the proportion of that is as high as 80% at different time steps: (a1) and (b1) step = 0, (a2) and (b2) step = 200, (a3) and (b3) step = 400, and (a4) and (b4) step = 600. The initial number of pedestrians in the waiting hall is 600 in each situation. Here, Pin donates the number of pedestrians left in the waiting hall and Pout donates the number of pedestrians escaped from the waiting hall at the specific time step.
Table 3.

Average evacuation steps in all conditions of different friend-group sizes.

.

On one hand, a 4 (friend-group size: single, two, three and four) × 2 (friend-group density: high and low) between subject ANOVA analysis reveals significant main effects on both friend-group size (F = 154.256; p < 0.001) and friend-group density (F = 218.501; p < 0.001). The interaction effect of friend-group size and friend-group density is significant (F = 59.781; p < 0.001) as well.

On the other hand, it is interesting to find that in the low friend-group density level there is no significant difference between group size 3 and group size 2 (p = 0.378), but all different friend-group sizes are significantly different from each other in high friend-group density level.

What we can observe from Fig. 9 is that a bigger friend-group size leads to a longer evacuation time, and the more people gather together to walk out, the more time it spends to escape out. Companions in a group always behave in a similar manner,[25] and they prefer to take care of each other and tend to keep pace with each other at the same velocity; thus, the in-group individual velocity will decrease with the group size increasing.[19] Meanwhile, a small group of companions may form and become an obstacle to other out-group pedestrians. Thus, both the overall velocity and evacuation efficiency decrease.[27]

Fig. 9. Case I: average evacuation time of all simulations trials with different friend-group densities (high friend-group density where the proportion of pedestrians in groups to total pedestrians is as high as 80% and low friend-group density where the proportion of that is only 20%) and different group sizes (single, two, three and four). The initial number of pedestrians in the waiting hall is 600 in each trial.
3.2. Case II: Simulation in the case of emergency

Once an emergency occurs, the waiting hall will be filled with panic and people will push each other and run towards the exits in order to escape from the waiting hall, thus leading to congestion and impacting the desired velocity of pedestrians. We suppose that the parameter of a low panic level is 0.3 while 0.7 represents a high panic level. Meanwhile, we set the situation as in the holiday state where the pedestrian density is 600 and the friend-group density is high (the proportion of pedestrians in groups to total pedestrians is 80%). Then we simulate each condition 50 times.

3.2.1. Simulation with different levels of panic

In this case, we set the size of friend-group to be integers ranging from 2 to 4, the desire velocity 3 m/s, and then discuss the variation in evacuation efficiency with the increase of the panic parameter [0, 0.9] (see Fig. 10).

Fig. 10. Case II: evacuation processes of a single trial with different panic parameters: (a1)–(a4) low panic level (0.3), (b1)–(b4) high panic level (0.7) at different time steps: (a1) and (b1) step = 0, (a2) and (b2) step = 200, (a3) and (b3) step = 400, and (a4) and (b4) step = 600. The initial number of pedestrians in the waiting hall is 600 in each trial. Here, Pin donates the number of pedestrians left in the waiting hall and Pout donates the number of pedestrians who escaped from the waiting hall at the specific time step.

The simulation results in the “low panic” and the “high panic” are shown in Fig. 10. The evacuation efficiency with high panic parameters is lower than that with low panic parameters. For example, there are only 165 people who evacuated from the waiting hall in high panic but 551 in low panic at the time step of 600, regardless of the effects of the friend-group density (see Fig. 10).

The evacuation time, similar to a U-shaped curve, first decreases and then increases with an increasing panic parameter (see Fig. 11). The results of the regression analysis yield the following function: T = 3379.19P2 − 1582.59P + 462.07 (F = 95.8445, P < 0.0001), where T is the evacuation time and P is the panic parameter. The overall evacuation time (efficiency) reaches its lowest (highest) level when P is approximately 0.23.

Fig. 11. Case II: evacuation time curve with different panic parameters (fifty trials in each condition).

Figure 11 shows the accumulative evacuation time with different panic levels. Evacuation efficiency improves when the panic starts to spread; however, it greatly decreases when the panic diffuses throughout the pedestrians. Finally, congestion may occur, and “fast is slow”.[20] The results indicate that the panic parameter should be managed within a reasonable range to improve the pedestrian evacuation efficiency and avoid stampedes and casualties.

3.2.2. Simulation with different friend-group sizes

As for different friend-group sizes when there is an emergency in the holiday state, the different panic level (high and low) is manipulated. In each condition, we set different friend-group sizes (single, two, three, and four) and controlled the density of friend-group in the high level.

A 4 (friend group size: single, two, three and four) ×3 (panic level: low, high and no) between-subject analysis of variance (ANOVA) test was conducted to analyze the evacuation time. The ANOVA analysis for evacuation time shows that both friend-group size and panic level have significant main effects (F > 100, P = 0.000, and F > 100, P = 0.000, respectively). Meanwhile, the friend-group size has a significant interaction with the panic level (F = 62.821, p < 0.001).

Figure 12 shows that the evacuation time varies at different panic levels. The efficiency with a low panic level is significantly higher than that with a high panic and also higher than that with no panic. Table 4 presents the average evacuation time for each condition. Whatever the panic level is, the friend group size exerts a significant negative effect on the evacuation efficiency. Moussaid[19] found that a larger group size caused the friend-group to walk slower in normal conditions. Our study finds that under panic, no matter which level it is, the average evacuation time varies with friend-group sizes (Fig. 12). Moreover, the effect is larger with high panic. Pedestrians are more aimless and anxious and can be more easily affected by people around them in high panic than in low panic.[6] The herd behavior will be more significant under a higher panic level.

Fig. 12. Case II: average evacuation time of all simulation trials with different panic parameters: high panic (0.7), low panic (0.3), and no panic (0) and different friend-group sizes: single, two, three, and four. The initial number of pedestrians in the waiting hall is 600 in each trial.
Table 4.

Average evacuation time: 600 passengers with different panic parameters and group sizes.

.

Finally, we draw four conclusions based on the above results. First, we found the evacuation thresholds in different operation states. Pedestrians with a high density require more time to escape, but the evacuation efficiency fluctuates with the density increasing, reaching the highest level when the pedestrian number is approximately 200 in low pedestrian density (in typical state) and 900 in high density (in the holidays) under normal operation cases. Second, the evacuation efficiency in the holidays is lower than that in the typical state. In addition, the friend-group size has a positive impact on the evacuation time apparently, that is, a larger size results in longer evacuation time. However, there is no significant difference between sizes of 2 and 3 in the typical state. Third, the panic parameters significantly influence the evacuation efficiency. As the panic parameter increases, the evacuation time first decreases and then increases, thus presenting a U-shaped curve. 0.23 is the most efficient panic level to evacuate pedestrians. In addition, if the panic level is overly high, it will lead to congestion, which also influences the evacuation time inversely. Finally, a larger friend-group size leads to lower evacuation efficiency no matter what the level of panic is in the holidays under emergency cases. The evacuation efficiency is the highest in the low panic level, which also confirms the third conclusion. Therefore, smaller friend-groups would be preferred in an evacuation process. In addition, the evacuation efficiency in a high panic condition reduces faster than that in a low panic condition with friend-group size increasing.

4. Conclusion

This study makes two main contributions. First, the study represents an advancement of researches on the social force model and multi-exit choice model. We further develop the social force model and combine it with a utility function to implement evacuation decisions, which is of importance in extending previous works. The modifications include not only the visual range and the relative friend attractiveness but also the congestion effect and design of multi-exit. These factors make the advanced model valid by describing the main observations of pedestrian dynamics in both normal operation cases and the emergency cases. Second, simulations are conducted in different situations of the actual subway station, which provides a safety threshold of pedestrian density and panic levels in the waiting hall. The model could be extended to other scenarios to find different thresholds for each scenario, which is critical to emergency management. The results regarding the relationship among evacuation time, pedestrian density, panic level and friend-group size are also useful for decision making with regard to contingency plans and emergency treatments.

This paper indeed has some limitations. First, our research focuses only on the waiting room in the subway station hall, ignoring the ticket checking machines and other equipment, which may be obstacles to evacuation. Second, we just assume that everyone could bear the external forces from outside and that no one falls down when the force surpasses his tolerance or no confliction occurs during the evacuation. However, if confliction occurs, people who get hurt will become obstacles. Thus, we will consider these factors and the effect of obstacles and the confliction on evacuation time in our future research. Third, many researchers have considered the calibration part recently while the calibration is not discussed in our current work. Zeng et al.[28] accomplished a more accurate calibration based on the observed dataset or the maximum likelihood estimation, which offers us useful information to make the results much more precise in further study.

Reference
1Helbing D1992Economic Evolution and Demographic ChangeBerlin/HeidelbergSpringer-Verlag33048330–48
2Barker J AHenderson D 1976 Rev. Mod. Phys. 48 587
3Henderson L 1971 Nature 229 381
4Hoogendoorn S PBovy P HDaamen W2002Pedestrian and Evacuation DynamicsBerlin/HeidelbergSpringer123
5Hughes R L 2002 Transp. Res. Pt. 36 507
6Helbing DFarkas IVicsek T 2000 Nature 407 487
7Helbing DMolnar P 1995 Phys. Rev. 51 4282
8Lu L LRen GWang WWang Y 2014 Chin. Phys. 23 088901
9You LZhang CHu JZhang Z H 2014 J. Appl. Phys. 115 224905
10Li D WHan B M 2015 Safety Sci. 80 41
11Li W HGong J HYu PShen SLi RDuan Q S 2014 Physica 420 28
12Yang X XDong H RWang Q LChen YHu X M 2014 Physica 411 63
13Wang LZhang QCai YZhang J LMa Q G 2013 Physica 392 2470
14Jiang LLi J YShen CYang S CHan Z G 2014 PLoS One 9 e115463
15Yang X XDong H RYao X MSun X B 2016 Chin. Phys. 25 048902
16Wei X GSong W GLv WLiu X DFu L B 2014 Simul. Model. Pract. Theory 40 122
17Lin PMa JLo S 2016 Chin. Phys. 25 034501
18Hou LLiu J GPan XWang B H 2014 Physica 400 93
19Moussaid MPerozo NGarnier SHelbing DTheraulaz G 2010 PLoS One 5 e10047
20Lakoba T IKaup D JFinkelstein N M 2005 Simulation 81 339
21Xu YHuang H JYong G 2012 Chin. Phys. Lett. 29 080502
22Helbing D1997Verkehrs DynamikBerlin/HeidelbergSpringer-Verlag
23Zainuddin ZShuaib M 2010 Transport. Theor. Statist. Phys. 39 47
24Seneviratne PMorrall J 1985 Transp. Plan. Technol. 10 147
25Helbing DMolnar PFarkas I JBolay K 2001 Environ. Plan. 28 361
26Mōri MTsukaguchi H 1987 Transp. Res. Pt. 21 223
27Sarmady SHaron FTalib A Z H2009Third Asia International Conference on Modelling & SimulationMay 25–29, 2009Bali, The Republic of Indonesia520
28Zeng W LChen PNakamura HIryo-Asano M 2014 Transp. Res. Pt. 40 143