† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11405078 and 11474140), the Fundamental Research Funds for the Central Universities, China (Grant Nos. lzujbky-2014-169 and lzujbky-2015-244), the Project sponsored by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, the State Education Ministry, and the National Students’ Innovation and Entrepreneurship Training Program (Grant Nos. 201410730069 and 201510730078).
For Li+ and Na+ ions scattered from high work function metal surfaces, efficient neutralization is observed, and it cannot be explained by the conventional free electron model. In order to explain these experimental data, we investigate the velocity-dependent neutral fraction with the modified Brako–Newns (BN) model. The calculated results are in agreement with the experimental data. We find that the parallel velocity effect plays an important role in neutralizing the Li+ and Na+ ions for large angle scattering. The nonmonotonic velocity behavior of neutral fraction is strongly related to the distance-dependent coupling strength between the atomic level and metal states.
Charge transfer processes between an atom/ion or molecule and a surface play an important role in influencing the charge states of the scattered particles and are used as a probe of the electronic structure of the surface. On the other hand, its implications extend over a large number of different fields, ranging from chemical reactions to electron emission and surface characterization. All these aspects have motivated intensively experimental and theoretical investigations.[1–16]
In general, resonant charge transfer (RCT) is considered experimentally and theoretically to be much more efficient in neutralization of alkali-metal ions scattered from metal surfaces. Resonant neutralization of alkali-metal ions on a metal surface involves a tunneling transition of an electron from an occupied level of the valence band to the atomic level of the projectile [i.e., Li (2s)] as it approaches the surface. Neutralization occurs if the Li (2s) energy level is below the Fermi level of the metal surface at a large distance. Conversely, resonant ionization takes place at a short distance where the atomic level is upward shifted due to image potential effects[13] and above the Fermi level. For a free electron metal surface, it is the so-called “standard” jellium free electron model in the literature. In this respect, the survival of neutrals depends on the electron transfer rate and the surface work function, as well as the interaction time that the projectile spends near the surface where RCT process occurs. Therefore, as the outgoing velocity of the scattered ion increases, the neutralization probability decreases monotonically. This has been confirmed by a number of experiments.[17–19]
Recently, the unexpected neutralization of Li+ ions scattered from noble metal surfaces with high work function has been observed.[20–24] These results show a nonmonotonic behavior of neutralization probability increasing at high and low incident energies. A time-dependent quantum mechanical approach is used to describe the resonant neutralization probability observed in Li+–Cu (111) collisions.[25,26] For high exit energies, it satisfactorily describes the measured neutralization probability, but it suffers some difficulties in explaining experimental results at low exit energies. On the other hand, it is hard for us to use the standard jellium free electron model to understand the results. According to this model, neutralization should be impossible for Li+ ions scattered from clean Cu (111) and Au (111) surfaces. Their work functions are 4.95 eV and 5.4 eV respectively, and the ionization potential of Li (2s) is 5.39 eV. The Li (2s) level lies above the Fermi level of the surface at a large distance where electron capture will be very inefficient. As a consequence, understanding the anomalous neutralization is highly desired.
This work aims to understand the anomalous neutralization based on quantum-mechanical calculations. We first revisit the previous BN model and modify it by considering the parallel velocity effect. Then we calculate neutral fractions by using this model for six collision systems from different groups. For Li+ scattering on Au (111), Cu (111), and Ag (111), the calculated results are in general agreement with the data at high perpendicular velocities. For Na+ scattering on Ag (001) and Cu (001) surfaces, the model including the parallel velocity effect can reproduce well the perpendicular velocity-dependent neutral fraction. In particular, calculated results present nonmonotonic behavior of the neutral fraction for Na+ scattering on Cu (001) with an exit angle of 45°, for which the reason is discussed in detail.
Brako–Newns model is a theory of resonant charge transfer based on the Newns–Anderson Hamiltonian. In this model, Auger or radiative neutralization, or neutralization into excited states of the scattered atom is ignored. BN model was described in detail elsewhere,[27] and the essentials of the model are given briefly below.
The non-degenerate valence level |a〉 of the energy εa of the moving atom is broadened by interaction with the states 〈k| of energy εk of the metal conduction band through matrix elements Vak = 〈a|V|k〉 where V represents the coupling of the atom to the metal.
Considering the conduction band, the atom valence state and the coupling between them, the Newns–Anderson Hamiltonian can be written as
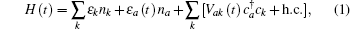

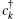

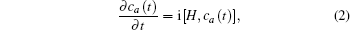
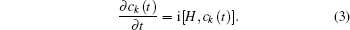
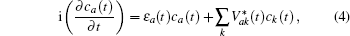
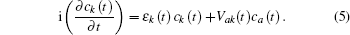
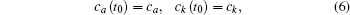
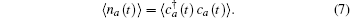
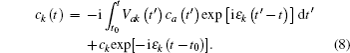

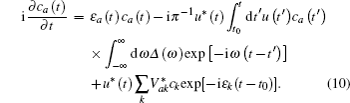
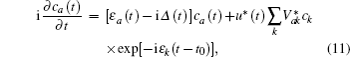
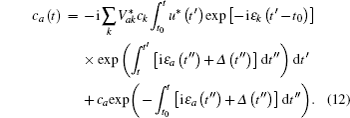
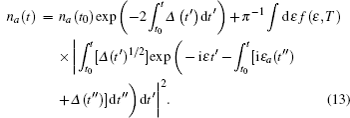
In Eq. (
The energy level of the atomic state εa(t) is approximately given by
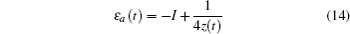
The time integration in Eq. (

In the model above, we have considered only the perpendicular exit velocity with respect to the surface. However, the energies of the metal electrons are shifted from their values in the rest frame of the projectile because of the motion of the projectile, which can cause significant change in the charge-transfer probability. In this case, the velocity component of the projectile parallel to the surface may be important. The parallel velocity effect has been discussed in previous papers[13,29–33] and we only give a brief introduction here.
According to the Galilean transformation,[34,35] we can define the Fermi momentum
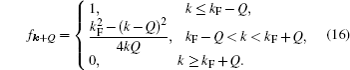
Figure
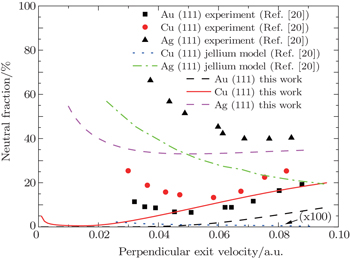 | Fig. 2. Plots of neutral fractions for Li+ scattering on Au (111), Cu (111), and Ag (111) versus perpendicular exit velocity. The incident angle with respect to the surface plane is 24° and the exit angle is 90°. Experiment:[20] (▲) Ag (111), (◼) Au (111), (●) Cu (111). Theory: the blue dotted line represents the jellium model results for Cu (111) enlarged by 100;[20] the green dashed-dotted line denotes the jellium model results for Ag (111);[20] the red solid, black, and purple dashed lines refer to the calculated results using the BN model, respectively. |
In the static case, neutral fraction would be either 100% or 0%, depending on whether the position of the unoccupied atomic level is above or below the highest occupied orbital in the surface, while for the dynamical scattering process, the neutralization depends not only on the relative position of energy levels but also on the interaction time. The Li (2s) level is above the Fermi level of Cu (111) (work function = 4.95 eV) when the ion surface distance is less than 15.5 a.u. where the coupling between the atomic level and the occupied states of the surface is very weak. In this respect, neutralization should be impossible for Li+ ions scattered from clean Cu (111) and Au (111) surfaces. The prediction of the jellium model for Cu (111) turns to deviate by a factor of several hundred and clearly does not reproduce the velocity dependence as shown in Fig.
For Ag (111) with a work function of 4.56 eV, the Li (2s) level is still below the Fermi level when the ion surface distance is larger than 8.2 a.u., where resonant electron capture occurs. Slower Li+ ions are more efficiently neutralized since they spend more time near the surface. As shown in Fig.
The experimental neutral fractions are measured for an exit angle of 90°, thus no parallel velocity effect is considered in the BN model here. We obtain Δ0 = 1.32 and α = 0.76 for Li (2s) from Ref. [28]. For Li+ scattered from Ag (111), our calculated results are also smaller than the experimental data compared with the jellium results, but are close to those in the case where the perpendicular exit velocity is larger than 0.07 a.u. For Li+ scattered from Cu (111), our calculated neutral fraction is nonmonotonic with perpendicular exit velocity. It has a similar trend and the same order of magnitude in comparison with the experimental data. For Li+ scattered from Au (111), our calculated neutral fraction can also give a similar trend and the same order of magnitude at larger perpendicular exit velocities. However, we do not see the increase at very low velocities.
We emphasize the nonmonotonic velocity dependences for Cu (111) and Au (111) surfaces here. The similar behavior for Li+ ions scattering on Au (110) and Pd (100) surfaces were also discussed in Ref. [23]. The calculated result increases with the increase of perpendicular exit velocity, which is related to the exponential increase of the atomic level width at a short ion surface distance. The large level width at a short distance implies the large charge transfer probability. Thus the initially formed neutrals at a short distance have less interaction time for electron loss with increasing perpendicular exit velocity, moving away from the surface. At a short distance, the initially formed neutrals of Cu (111) are more than those of Au (111) due to the energy level coupling effects, thus the neutral fraction of Cu (111) is larger than that of Au (111) at a large perpendicular exit velocity. In contrast, at a much lower perpendicular exit velocity, neutral fraction increases again. It may be attributed to the weak energy level coupling for electron capture at a relatively large distance. The long interaction time favours electron capture for a very low perpendicular velocity. The Li (2s) level is further above the Fermi level of Au (111) compared with those of Cu (111) and Ag (111) at a larger distance, and the finite energy width of the atomic level does not overlap with the occupied state of Au (111) anymore, so the calculated neutral fraction of Au (111) is close to zero at a very low exit velocity.
The jellium model cannot reproduce the nonmonotonic velocity dependences for Cu (111) and Au (111) surfaces where the atomic level is above the Fermi level at a large distance. On the other hand, the BN model does not reproduce the experimental data of (111) surfaces well, which could be attributed to the effects of bandgap and surface states on charge transfer process that have not been taken into account in the jellium model and in this work.[18,36–41] The L band gap of the (111) surface should lead to a strong decrease in electron loss from the populated Li level to the conduction band.
Recently, Ray et al.[2] reported neutral fraction for Na+ ions scattering on Ag (001) as shown in Fig.
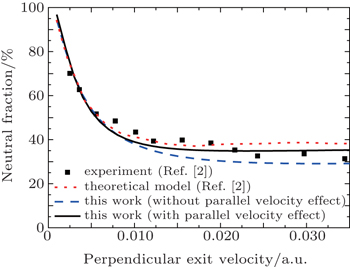 | Fig. 3. Plots of Neutral fraction for Na+ scattering on Ag (001) versus perpendicular exit velocity. The incident angle with respect to the surface plane is 35° and the exit angle is 35°. Experiment: (◼).[2] Theory: the red dotted line represents the calculated results from Ref. [2]; the black solid and blue dashed lines refer to calculated results by using the modified BN model with and without the parallel velocity effect, respectively. |
This experiment is performed at an exit angle of 35° measured with respect to the surface plane. Δ0 = 2.5 and α = 0.81 for Na (3s) are chosen to fit the exponential data to the calculations of Nordlander and Tully.[28] We first calculate the neutral fraction by using the BN model without the parallel velocity effect. Our calculated results are in good agreement with theirs at low perpendicular velocities, and are slightly smaller than the experimental data and their calculated result at relatively high velocities. If we consider the parallel velocity effect in the BN model, then the calculated results have good consistency with their experimental data in the whole velocity range.
The Na (3s) level (ionization energy = 5.14 eV) is still below the Fermi level of Ag (001) (work function = 4.40 eV) for an ion surface distance of about 9.2 a.u. and is above it close to the surface. Due to the small work function of Ag (001), the neutralization is mainly determined at the distance where resonant capture is predominant. The lower the velocity, the higher the neutral fraction is. This is very similar to the case of Li+ scattering on Ag (111) as shown in Fig.
In Fig.
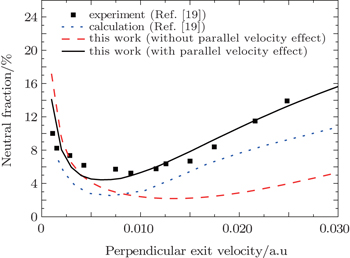 | Fig. 4. Variations of neutral fractions for Na+ scattering on Cu (001) with perpendicular exit velocity. The incident angle with respect to the surface plane is 45° and the exit angle is 45°. Experiment: (◼).[19] Theory: the blue dotted line represents the calculated result from Ref. [19]; the black solid and red dashed lines denote the calculated results by using the modified BN model with and without the parallel velocity effect, respectively. |
The calculations in Ref. [19] are lower than the experimental data, and present the nonmonotonic trend. The lifetime and energy of the Na (3s) resonance we use here are the same as those used in Fig.
Like the data shown in Fig.
| Table 1. The crossing distance corresponding to the distance where the atomic level is above the Fermi level of the surface. . |
It is noted that the experiments mentioned above are performed for large scattering angles, where the nonmonotonic neutral fractions have been observed for high work function surfaces. For grazing angle scattering, the incorporation of kinematic effects into terms of a frame transformation, named the parallel velocity effect, is significant and even changes the velocity dependence of neutral fraction.[32,37,43,44] The neutralization of Cs scattered under a grazing angle of incidence from a Cu (111) surface was reported by Borisov et al.[43] The 6s Cs orbital is bounded by 3.89 eV for the free atom, which is far above the Fermi level of Cu (111), however, the bell-shaped neutral fraction is observed as a function of parallel velocity and the maximum of neutral fraction is about 15%. Borisov et al. well developed the nonperturbative coupled angular mode method. Combining the rate-equation, they give a good theoretical description at a quantitative level.
Does the modified BN model work well for grazing scattering configurations? As an example, figure
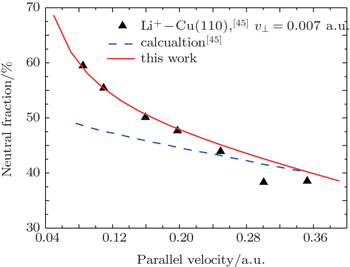 | Fig. 5. Neutral fractions for Li+ scattering on Cu (110) as a function of parallel velocity. The velocity component normal to the surface is kept to be about 0.007 a.u. Experiment: (▲).[45] Theory: the blue dashed line represents the calculated result from Ref. [45]; the red solid line denotes the calculated results by using the modified BN model with the parallel velocity effect. |
In this work, the neutralizations for Li+ ions scattered from clean Ag (111), Cu (111), and Au (111) surfaces are calculated. For Cu (111) and Au (111) surfaces, we find that the BN model involving the energy level width can give a better description than the conventional jellium model from which the results are two orders of magnitude smaller. Moreover, for Na+ ions scattered from Ag (001) and Cu (001) surfaces, we use the modified BN model including the parallel velocity effect and achieve good agreement with the previous experimental data. It suggests that the parallel velocity effect is crucial for specific collision partners even for large-angle scattering.
In general, for a collision system with small crossing distance, the velocity dependence of neutral fraction is monotonic, which can be easily understood with the jellium free electron model, while for a collision system with large crossing distance, the velocity dependence of neutral fraction is nonmonotonic. The nonmonotonic velocity dependence can be understood as follows: at a low perpendicular exit velocity, the finite energy level width at a relatively large distance results in electron capture. The long interaction time further favours electron capture for very low perpendicular velocities. A large perpendicular exit velocity corresponds to a short ion surface distance where the large level width results in high charge transfer probability. Moreover, the initially formed neutrals at a short distance, move away from the surface thus have less interaction time for electron loss with increasing perpendicular exit velocity.
In conclusion, the modified BN model has no free parameters. For large-angle scattering, this model gives the correct magnitude and trend for alkali-metal ions scattered from high work function metal surfaces. But there are still some limitations for the BN model, such as the effects of band gap and surface states. Thus, to study the lifetime and energy level of the projectile on a realistic metal surface, further relevant theoretical work is necessary in the future. On the other hand, for grazing angle scattering, this model provides in principle another theoretical method although Borisov’s model is successful. The relevant study is in progress.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 |



