† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61377109 and 11374007).
A system for measuring terahertz spectrum is proposed based on optical interferometer theory, and is experimentally demonstrated by using a backward-wave oscillator as the terahertz source. A high-resolution, high-precision interferometer is constructed by using a pyroelectric detector and a chopper. The results show that the spectral resolution is better than 1 GHz and the relative error of frequency is less than 3%. The terahertz energy density distribution is calculated by an inverse Fourier transform and tested to verify the feasibility of the interferometric approach. Two kinds of carbon-fiber composites are imaged. The results confirm that the interferometer is useful for transmission imaging of materials with different thickness values.
Terahertz waves are those waves whose frequencies are in the frequency range of 0.1 THz–10 THz, the portion between the infrared band and the millimeter wave in the electromagnetic spectrum.[1,2] Terahertz waves can penetrate paper, leather, foamed plastic, and other materials. Furthermore, they are safe for the human body and for other organisms.[3] In addition, terahertz waves have special applications in transmitting information for broadband wireless communications.[4] With the advent of various terahertz sources, such as the Gunn oscillator, terahertz quantum cascade lasers, and the backward-wave oscillator (BWO), the need for precise frequency spectrum measurements in various noisy environments has increased. However, recent research suggests that there are only a few precise, effective methods of detecting terahertz waves over their full frequency range.
In order to quantify the physical properties of a terahertz wave, two main methods for spectrum detection have been proposed so far: heterodyne and interferometric techniques. Of these, the heterodyne method is always used by electronic and electro-optic sampling.[5–10] However, the electronic heterodyne method can only characterize a narrow band of frequencies within the terahertz spectrum in the course of a single measurement, and precise measurements of high frequencies are difficult to obtain; electro-optic sampling of the heterodyne method is used to detect the spectra of pulse terahertz wave sources, but the signal-to-noise ratio is usually poor. Furthermore, the existing heterodyne measure system often requires an extra mock-locked laser source on the gap of the photoconductive antenna (PCA) in the detecting units, which increases the cost and the complexity of the experiment. The interferometric method, which has typically been used for detecting laser beam spectra, has emerged as a modern method for terahertz wave metrology.[11–13] The interferometric method enables the real-time detection of single-frequency continuous terahertz sources within 6 GHz,[14] while the optical interference systems can extend the measurable frequency range of the terahertz source by using interference principles. Optical interference systems are real-time, quantitative, and cost-effective; and they have been used to measure broadband pulsed terahertz waves.[15] In the present paper, we discuss an optical interference measurement system that can detect the full frequency range and energy density of continuous terahertz waves. Previous research on pulsed terahertz waves,[16] suggests that this method has the potential for covering the entire terahertz band; however, the BWO source that we used is limited to relatively low output frequencies ranging from 160 GHz to 260 GHz. The experimental results show that the spectral resolution is better than 1 GHz and the relative error of frequency is less than 3%. In the recent research,[17–21] the energy density of a terahertz wave can be tested with the interferometric system, which can be measured in frequency-multiplied broadband terahertz sources and the necessary information to create images of the measured object can be obtained by two-dimensional (2D) scanning.
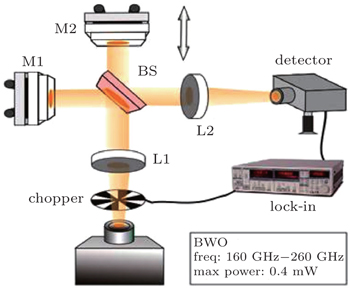
The terahertz interferometer system used in the study is shown in Fig.
The terahertz wave produced by the BWO is modulated by a chopper and collimated with lens L1 (a teflon lens with a diameter of 100 mm and a focal length of 100 mm). The parallel light beam from L1 is divided into two parts by a high-resistivity silicon wafer acting as a beam splitter (BS); this wafer is 0.5-mm thick. One of the split beams, which is reflected by the fixed mirror, acts as a reference beam, while the other beam, which is reflected by the movable mirror, serves as a measurement beam. The reference beam and the measurement beam are re-combined in the same direction after passing through the BS the second time. The combined beam is focused onto the detector by lens L2 (the focus lens has a diameter of 50 mm and a focal length of 50 mm).
Because of the pyroelectric effect, the pyroelectric detector generates a voltage signal proportional to the intensity of the incident interference beam. A lock-in amplifier analyzes the signals generated by the detector through using the chopper frequency as a reference. With 10-Hz modulation of the chopper and 10-ms lock-in time, the minimum detectable power (Imin) from the BWO is 0.4 μW. According to the formula: DR = 20lg(Imax/Imin) along with the fact that the maximum output power (Imax) of the BWO is 0.4 mW, the dynamic range of the system is calculated to be 60 dB.
Our terahertz spectrum analyzer is based on the Michelson interferometer optical system. According to interferometer theory, the interference intensity (I) can be expressed as
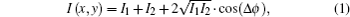
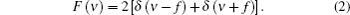
Since F(ν) in Eq. (
In addition to acquiring the terahertz spectrum, we can also obtain the energy density of the incident beam by inverse Fourier transformation of the interference intensity. The theory can be expressed as follows.
If the spectral radiation energy density of the terahertz source is S′(x), and the intensities of the detection and reference beams are equal, then the interference intensity can be expressed as
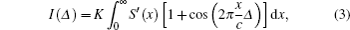
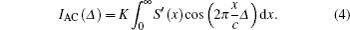
Thus, the energy density of light source S′(x) can be obtained by inverse Fourier transforming the AC component of the interference intensity as
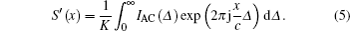
The chopper signal is a square wave signal, hence, the modulated intensity of the terahertz wave can be expressed as follows:
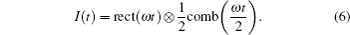
Using the voltage signal received by a pyroelectric detector as the input for the lock-in amplifier, and the chopper output as reference, the output of the lock-in amplifier can be expressed as
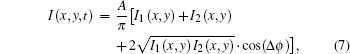
Equation (
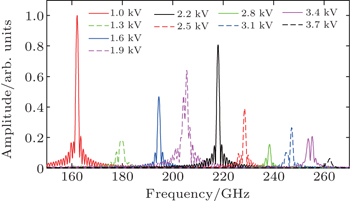
The output frequency of the BWO is controlled by its input voltage. In this study, selected frequencies in the range from 160 GHz to 260 GHz (corresponding to input voltages between 1.0 kV and 3.7 kV) are used as the test frequencies. The range of travel of the stage is 152 mm and the corresponding spectral resolution is 0.9872 GHz. Figure
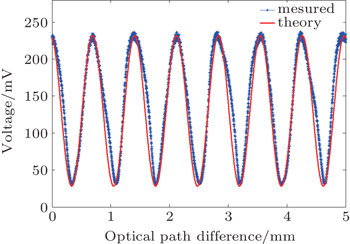 | Fig. 2. 260-GHz measurement result. The solid line denotes the measured interference intensity; the dotted line gives the result of fitting to a sinusoidal waveform. |
Figure
The output frequency of the BWO is a function of the input voltage; their relationship can be approximated by the following formula:
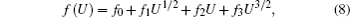
| Table 1. Input voltages and output frequencies. . |
The frequency test results (Fig.
Using the frequencies specified by the manufacturer’s instruction manual for the BWO, the standard frequency curve can be obtained as shown by the black solid line in Fig.
 | Fig. 4. Curve of the calculated frequency (black line) compared with the experimentally measured results (red dots). |
Figure
According to the communication principle, the resolution σ of the system is proportional to the maximum optical path difference, or the scan range of the stage. When the scanning range of the system is L, the maximum delay time is 2L/c. The corresponding minimum frequency resolution is inversely proportional to the maximum delay time; accordingly, the resolution of the system can be expressed as
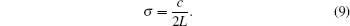
Equation (
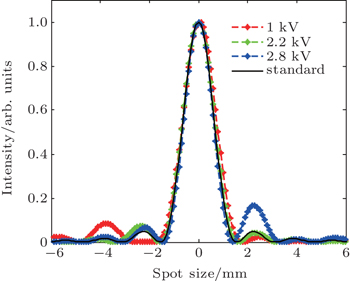
The 2D distribution of the test result is shown in Fig.
The main peaks of the measured curves in Fig.
To demonstrate an important interference imaging application, two different composite materials, composed of carbon fiber and reinforced plastic, are pasted on M1 and used for transmission-type imaging at 206 GHz, which is the maximum frequency at which the BWO can produce sufficient output power. M1 is mounted on a computer-controlled X–Y stage in steps of 0.5 mm, and placed at the focal point of a new focusing lens (not shown in Fig.
In this work, a measurement system for terahertz spectra and energy densities is proposed based on an optical interferometer. The spectra can be tested precisely by varying the scanning length of the reflection mirror. Within the frequency range from 160 GHz to 260 GHz of the BWO used as a terahertz wave source, the experimental results show a relative error of frequency less than 3% and a spectral resolution better than 1 GHz. Furthermore, the system also has imaging ability. In this study, two kinds of carbon-fiber composites are imaged. The imaging results show that the resolution of the system is approximately 1 mm. Consequently, this type of optical system can be used in transmission materials for terahertz wave imaging. The method can be considered as a coherent imaging tool that can reveal the interior characteristics of the sample, and has widespread applications in terahertz imaging and sensing.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 |