Cold atomic beams have desirable features such as high flux at low mean velocity, narrow velocity distribution, and small divergence. They are widely used in fields of atom interferometry,^[1–4] atomic clocks,^[5–8] cold atom collisions,^[9,10] and atom optics.^[11] Besides, they are required for fast loading a magneto–optical trap (MOT) in an ultra high vacuum (UHV).^[12]

The cold atomic beams can be produced by using a Zeeman slower^[13] or an isotropic-light tube^[14] to decelerate a thermal atomic beam along its propagation axis, or by extracting from a vapor MOT directly. Compared to the decelerator, the MOT source is preferred because of its narrower velocity distribution and higher brightness.^[15] The MOT source can be implemented in various configurations, including the low-velocity intense source (LVIS),^[16–18] the moving molasses (MM) MOT,^[19] the pure two-dimensional (2D) MOT,^[20] and the 2D⁺ MOT.^[21]

The 2D⁺ MOT source is a configuration in which the two-dimensional magneto–optical trap is complemented with axial laser beams. With larger cooling volume and the capability of cooling or pushing in the axial direction, the 2D⁺ MOT can produce a higher atomic flux at a similar or even lesser power consumption than other configurations of the MOT source. For the axial laser beams, the configuration can be a pair of cooling beams (pushing and retarding beams),^[21–24] one hollow beam,^[25,26] or one pushing beam.^[27–34] For the pair-of-beam configuration, the atoms are both cooled and pushed in the axial direction, which results in a high flux and a narrow axial-velocity distribution. Nevertheless, the laser power and detuning are mainly adapted to axial cooling rather than pushing. Considering the physical fact in the MOT, cooling decelerates atoms but pushing accelerates atoms. The pushing beam cannot be substantially optimized until its power and detuning is regulated independently. Besides, the axial laser light coming out along the cold atoms is rather intense, resulting in considerable light shift. For the one-hollow-beam configuration, the laser beam is far blue-detuned and shaped into a Laguerre–Gaussian donut mode. Cold atoms in the MOT can be channeled over a long distance with small divergence. Thus the atomic density is increased compared to that in a freely-propagating beam. In Carrat et al.’s recent study, the increase by a factor of 200 is achieved.^[26] However, without axial cooling, the cold atoms from this kind of 2D⁺ MOT have undesired broad axial velocity distribution, tens of meters per second. For the one-pushing-beam configuration, the pushing beam can be a thin near-resonant beam,^[27–32] or an intense far-detuned one.^[33,34] These studies, especially the 2D^2p MOT by Park et al.,^[32] indicate that the pushing beam should have specific power and detuning. Though the pushing beam is optimized, without axial cooling, the efficiency of this kind of 2D⁺ MOT is lower than the first configuration.

In general, to obtain an intense cold atomic beam with narrow velocity distribution with the 2D⁺ MOT, the axial cooling and pushing is indispensable. Limited by the configurations above, the 2D⁺ MOT cannot be fully optimized. Besides, for experiments based on a cold atomic beam, such as atom interferometry and atomic clock, the problem of the light shift due to the pushing beam should also be resolved.^[3,4] To substantially optimize the 2D⁺ MOT and significantly suppress the light shift, we propose a novel configuration for the axial laser beams. In the scheme, a pair of counter-propagating hollow laser beams are applied for axial molasses cooling. Another homocentric thin laser beam is used for pushing. The hollow beams and the pushing beam are functionally separated and do not interfere with each other. We propose “2D-HP MOT” to name this new scheme distinguishing it from the traditional 2D⁺ MOT, where H stands for the hollow cooling beams and P the thin pushing beam.

This paper is organized as follows. In Section 2, we explain the basic principle of the 2D-HP MOT, including the rate and trapping equation, the atomic flux analysis and the light shift effect. In Section 3, we present a detailed description of the experimental setup and the measurement of the cold atomic beam. The experimental results and discussions are arranged in Section 4. We summarize and give an outlook on future experiments in Section 5.

The flux of the cold atomic beam extracted from the 2D-HP MOT is determined by the rate equation, the relationship between the loading rate and the loss rates. The loading rate R indicates the capture capability of the MOT, which is derived from the flux through the surface of the cooling volume of atoms with a radial velocity below the capture velocity v_r < v_c.^[20,21,35] Its definition per axial velocity interval [v_z,v_z + dv_z] in cylindrical coordinate is^[20]

The loss of the cold atoms within the MOT is mainly caused by three factors, which are the collisions between the cold atoms and the thermal background vapor (“cold–hot” collisions), the collisions between two cold atoms (“cold–cold” collisions), and the outcoupling from the cold atomic cloud into the beam, respectively. The loss rate due to the “cold–hot” collisions is proportional to the density of the thermal background vapor, which can be written as Γ_trap = nσv_rms.^[35] Here v_rms is the root-mean-square (rms) velocity of thermal atoms, and σ is the effective collision cross section. For a cesium atom, σ is 2 × 10⁻¹³ cm². The loss rate caused by the “cold–cold” collisions is β_NN/V, growing as the density of the trapped cold atoms. Here β_N is the trap-loss parameter, which contains the probabilities for inelastic processes, such as fine-structure-changing collisions, radiative escape, and photoassociation. The study on β_N has been an interesting and important topic. Both theoretical and experimental works verify that β_N increases linearly with the MOT laser intensity.^[9,36,37] The loss rate due to the outcoupling is called the outcoupling rate Γ_out, which represents the capability of the pushing laser beam extracting the cold atomic beam from the MOT. It can be simply written as Γ_out = 1/t_out, where t_out is the time for pushing the cold atoms out of the MOT.^[21]

In the 2D-HP MOT, the time t_out is determined by the cold atom velocity and the distance d that atoms travel out of the MOT. Under the radiation pressure from the pushing laser beam, the velocity is affected by the power and detuning and varies as

In addition to the three loss rates above, the heating effect due to the pushing laser beam also results in the loss of cold atoms. Obviously, this loss rate is related to the intensity and detuning of the pushing laser, and we assumed it can be expressed as Γ_heat ∼ αI · s′, where α is a coefficient, I is the pushing laser intensity, and s′ = s/(1 + s + 4(δ − kv − δ_heat)²/Γ²). The parameter δ_heat corresponds to the most effective heating detuning.

At the balance of loading and loss, the rate equation of the 2D-HP MOT can be written as^[20,21]

According to Eq. (4), the dependence of the total atomic flux on the outcoupling rate can be calculated. The results calculated with different loading rates, 5 × 10¹⁰ atoms/s, 1 × 10¹⁰ atoms/s, and 5 × 10⁹ atoms/s are as shown in Fig. 1. Here the other loss rates are treated as constant values. A high loading rate results in an intense flux and the total atomic flux increases with the outcoupling rate until saturated. Thus, to achieve an intense cold atomic beam, both the loading rate and the outcoupling rate should be adjusted to high values.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The dependence of the total atomic flux on the outcoupling rate at different loading rates: 5 × 1010 atoms/s (black solid line), 1 × 1010 atoms/s (red dashed line), and 5 × 109 atoms/s (blue dotted line).

With trapping and sub-Doppler cooling, the velocity of the cold atoms in the MOT is close to zero value and follows a rather narrow Maxwell distribution.^[21] Taking the average distance as d = L/2 = 20 mm and the initial axial velocity v_z(0) = 0, the outcoupling rate Γ_out to different pushing power (beam diameter = 3 mm) and detuning can be calculated with Eq. (2) and the boundary condition. With the loading rate 5 × 10¹⁰ atoms/s, the dependences of the atomic flux on the pushing power and detuning are then obtained. In these results, the variations of the heating rate Γ_heat with the pushing laser parameters have been taken into calculations. As shown in Fig. 2(a), the atomic flux increases within a certain range of the pushing power. The resonant pushing beam generates the highest flux in low-power condition. But when the pushing power increases to a certain value, the atomic flux begins to decrease. This decrease is not found in the curves of the non-resonant conditions, because the pushing power is not enough. With the same detuning range, the red-detuned beam performs better than the blue-detuned one. In Fig. 2(b), we can find that the atomic flux decreases when the pushing laser detuning increases. As the pushing power grows, the laser frequency of the peak flux red-shifts, and the flux distribution broadens. In high power conditions, the curve becomes much more asymmetric. These flux variations of the zero-velocity atoms provide a practical guidance for the pushing optimization in the 2D-HP MOT.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. The calculated atomic flux of the zero-velocity atoms: (a) the flux varying with the pushing power of various detunings, 0Γ (black solid line), −3Γ (red dashed line), +3Γ (blue dotted line), −5Γ (magenta dashed-dotted line), and +5Γ (green dash-dot-dot line); (b) the flux varying with the pushing detuning of various power, 20 μW (black solid line), 50 μW (red dashed line), 100 μW (blue dotted line), and 200 μW (magenta dashed-dotted line).

In addition to the independently-optimized atomic flux, the light shift is another main concern of the 2D-HP MOT. The light shift Δω_F to the cesium atom is^[38]

The experimental setup consists of the vacuum system, the quadrupole magnetic field, and the laser system. The cesium vapor cell is formed by a 55-mm diameter, long circular quartz tube. Both ends of the tube are connected to the pump system. Near the detection region, an ion pump is added to keep a higher vacuum. A temperature-controlled cesium reservoir is connected to the tube beside the MOT via a vacuum valve. In the experiments, the vacuum is 1.2 × 10⁻⁵ Pa at the MOT, and 3.5 × 10⁻⁶ Pa at the detection region.

The quadrupole magnetic field is generated by two orthogonal pairs of 140 × 100-mm rectangular coils, as shown in Fig. 3. The coils are spaced by 110 mm and symmetric in XY directions. Along the Z direction, it retains no magnetic field. The XY magnetic field gradient is set to be 10 Gs/cm (1 Gs = 10⁻⁴ T).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The schematic diagram of the 2D-HP MOT. M1, M2: mirror; λ/4, λ/2: wave plate; PBS: polarized beam splitter; HR-coated λ/4: λ/4 wave plate coated with high-reflectivity film; σ+, σ−: circular polarization; Ω: collection angle; PD: photodiode.

The diode laser system includes a DBR laser, a DFB laser and an extended cavity diode laser (ECDL), which are all frequency-locked using the standard saturation absorption (SA) techniques. The DBR laser beam is split into two parts: one major part is used for the cooling and the other part is used as the pushing beam. The cooling frequency is detuned −2.5Γ from the cycling transition

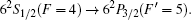
The configurations of the laser beams are presented in Fig. 3. To obtain a large cooling volume, the XY laser beams are expanded into 40 mm × 20 mm rectangles by the cylindrical lens. Containing 27-mW cooling laser and 4-mW repumping laser, the XY laser beams are circularly polarized and retro-reflected by λ/4 wave plates (50 mm × 25 mm). The λ/4 wave plates are coated with high-reflectivity film on the back to make the laser beams couterpropagate and polarize reversely. In this arrangement, the laser power requires higher values because of the imbalanced-laser effect.^[15] In the axial direction, a hollow beam, which is linearly polarized and retro-reflected by another λ/4 wave plate, is applied for cooling as designed. The hollow beam is generated by an axicon, with the inner diameter 5 mm and the outer diameter 16 mm, and the power is 15 mW. At the center of the wave plate, a 1-mm aperture is drilled for atomic beam extraction. The pushing laser beam (beam diameter = 3 mm) is combined with the hollow beam by a polarized beam splitter (PBS). The pushing beam, the hollow beam and the aperture are aligned concentrically. In the experiment, a part of the pushing laser would leak out of the aperture and go along with the atomic beam. Here it is marked as “leaking laser light.”

The plug laser and the probe laser are used for diagnosing the cold atomic beam. The plug laser is 2.5 mW with a 5-mm diameter, and the probe laser is a 200-μW rectangular beam (15 mm × 2 mm). The probe laser beam and plug laser beam are separated by 300 mm. To enhance the fluorescence signal, the probe laser beam is retro-reflected. The fluorescence emitted from the cold cesium atoms is collected by the lens assembly with a spatial angle Ω, and measured by a photodiode (Hamamatsu S3204-08). A time-of-flight (TOF) method is used to measure the atomic beam flux and the axial velocity distribution. Suddenly opening the plug beam, the cold atoms would be pushed away from the axis. The time dependence of the decaying fluorescence signal S(τ) is detected. Then the axial velocity distribution Φ(v_z) can be deduced as

In experiments, the 2D-HP MOT is realized, where the axial cooling and pushing are accomplished by a hollow beam and another pushing beam, respectively. The dependences of the total atomic flux on the pushing power and detuning are measured, and a comparison is made between the 2D-HP MOT and the traditional 2D⁺ MOT based on the experimental results.

4.1. Demonstration for the 2D-HP MOT

In the 2D-HP MOT, the hollow beam keeps the loading rate but makes no contribution to the atomic beam extraction, and the pushing beam regulating the outcoupling rate determines the atomic beam extraction. In experiment, the pushing beam is 15 μW and resonant with the 4 → 5′ cycling transition. By sweeping the probe laser frequency around the 4 → 5′ cycling transition, the hyperfine spectral lines of the cold atomic beam in different conditions are measured as shown in Fig. 4(a). When only the hollow beam is on, the cold cesium beam is not extracted, and the spectral line (blue dotted line) is almost invisible. When only the pushing beam is on, the spectral line (the red dashed line) is still very weak, because the loading rate is rather low without the axial cooling. When both the hollow and pushing beams are on, the spectral line (black solid line) becomes very distinct and the signal is enhanced by one order of magnitude of that in the only-pushing condition.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Signal of the cold cesium atomic beam in different conditions: (a) the 4 − 5′ hyperfine spectral lines: both hollow and pushing beams on (black solid line), only pushing beam on (red dashed line), only hollow beam on (blue dotted line); (b) the axial velocity distribution: only pushing beam on (red dashed line), both hollow and pushing beam on (black solid line).

Besides, the axial velocity distribution in the pushing-only condition and the cooling-pushing condition is measured, as shown in Fig. 4(b). When only the pushing laser is on (red dashed line), the mean velocity of the distribution is 7.6 m/s and the total flux is 4.18 × 10⁹ atoms/s. When both the cooling and pushing are on (black solid line), the mean velocity is reduced to 7.0 m/s, and the total flux is enhanced to 3.03 × 10¹⁰ atoms/s. The flux increases by about one order of magnitude, just as that of the spectral lines.

These results demonstrate that the 2D-HP MOT works as designed. The hollow beam keeps the loading rate and the pushing beam determines the outcoupling rate. An intense cold atomic beam is extracted when both laser beams are on.

4.2. Dependences on pushing parameters

In experiments, the dependence of the total atomic flux on the pushing power is measured at the detuning of −7Γ, −5Γ, 0Γ, +5Γ, and +7Γ, as shown in Fig. 5(a) and the results are the mean values of three measurements. The variations present that the total atomic flux would increase with the pushing power within a power range. This increase is caused by the enhanced outcoupling rate. At zero-detuning condition, a weak pushing power leads to a relatively high flux and the atomic flux reaches 3.03 × 10¹⁰ atoms/s, when the power is only 15 μW. After that, the atomic flux begins to decrease. The atomic flux at red detuning is higher than that at blue detuning. The maximum flux in experiments, 4.02 × 10¹⁰ atoms/s, is obtained when the pushing power is 400 μW and the detuning is at −5Γ. These results are in agreement with the theoretical calculation in Fig. 2(a).

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. The dependences of the total atomic flux on the pushing parameters: (a) the dependence on the pushing power at different pushing detuning:−7Γ (black square line), −5Γ (red circle line), 0Γ (green diamond line), +5Γ (blue up triangle line), and +7Γ (magenta down triangle line); (b) the dependence on the pushing detuning at different pushing power: 20 μW (black square line), 60 μW (red circle line), 100 μW (blue up triangle line), and 150 μW (magenta down triangle line).

Besides the 0Γ condition, the experimental results of +5Γ and +7Γ in Fig. 5(a) also show a clear decrease. The turning point of laser power has the minimum value at zero-detuning condition, and increases as the pushing detuning extends.

As discussed in Section 2, the heating effect caused by the pushing laser around the axis accounts for the flux loss. The heated atoms will escape from the MOT, rather than being pushed out, if its velocity is faster than the capture velocity. In experiments, the section of the pushing laser beam is a little larger than the aperture, which can generate a more serious heating effect when the pushing laser is suitably blue-detuned.

Additionally, the dependence of the total atomic flux on the pushing detuning at pushing power of 20 μW, 60 μW, 100 μW, and 150 μW are measured as shown in Fig. 5(b). When the power is as low as 20 μW, we can find that the total atomic flux has a higher value when the frequency of the pushing laser is close to resonance. With the pushing power increasing, the laser frequency corresponding to the peak flux red-shifts, and the high-flux range broadens. Besides, as the pushing power increases, the atomic flux near resonance decreases, instead of increasing as the outcoupling rate. These variations are consistent with the theoretical calculations in Fig. 2(b). Besides, it should be mentioned that the results in Fig. 2(b) are calculated with a zero axial velocity. The narrow Maxwell distribution of the cold atoms trapped in the MOT is not included. Thus, the variations of the flux with detuning in experiment is more broadened than that in theory. To fully reflect the reality, the velocity distribution of the cold atoms inside the MOT should be measured. However, limited by the experimental setup, a time-of-flight (TOF) measure around the MOT was not carried out in our experiments.

4.3. Comparison with the 2D⁺ MOT

To compare to the traditional 2D⁺ MOT with a pair of cooling beams, the 2D-HP MOT is modified by blocking the pushing beam and replacing the hollow laser beam by a regular Gaussian beam. The laser beam has the same diameter, power, and detuning as the previous hollow beam. The central intensity of the Gaussian beam is the pushing intensity, 8.06 mW/cm². Other parts of the setup in Fig. 3 remain unchanged. Thus, except the fixed pushing, other parameters of the 2D⁺ MOT are the same as the 2D-HP MOT.

The axial velocity distribution of the cold atomic beam extracted from the 2D⁺ MOT centers at 7.2 m/s with an FWHM of 3.2 m/s, the black solid line shown in Fig. 6(a). The total atomic flux is 2.54 × 10¹⁰ atoms/s.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (a) The axial velocity distributions of the cold atomic beams: 2D+ MOT (regular Gaussian beam, black solid line), 2D-HP MOT (0Γ, 10 μW, red dashed line), and 2D-HP MOT (-5Γ, 400 μW, blue dotted line). (b) Schematic diagram of the pushing beam expander.

To make a comparison with the 2D⁺ MOT, the velocity distributions obtained in the 2D-HP MOT with the pushing parameters (−5Γ, 400 μW) and (0Γ, 10 μW) are plotted in Fig. 6(a). For the parameters −5Γ and 400 μW, the pushing laser intensity is 5.66 mW/cm². In this condition, the total atomic flux reaches the experimental maximum, 4.02 × 10¹⁰. The velocity distribution centers at 8.2 m/s with an FWHM of 4.2 m/s (the blue dotted line in Fig. 6(a)). Compared to the 2D⁺ MOT, the total atomic flux is enhanced by 60%.

For the parameters (0Γ, 10 μW), the pushing laser intensity is 0.14 mW/cm². In this condition, the velocity distributes around 6.8 m/s with an FWHM of 2.8 m/s (the red dashed line shown in Fig. 6(a)). The atomic flux is 2.64 × 10¹⁰ atoms/s, similar to the 2D⁺ MOT. However, the 0.14-mW/cm² pushing beam is much weaker than that of the 2D⁺ MOT, helping effectively suppress the light shift caused by the leaking laser light. According to Eq. (5), the light shift of the ground state hyperfine transition between 6²S_1/2(F = 3) and 6²S_1/2 (F = 4) caused by the thin pushing laser is about −19.76 kHz, which is about 20 times lower than the one, −436.82 kHz, caused by the Gaussian beam. Moreover, with the same laser power instability, the light shift fluctuation is also drastically reduced. This suppression can greatly improve the signal in atomic clocks or atom interferometers.

Furthermore, with a minor adjustment to the thin pushing beam like those in Refs. [26] and [29], the light shift can be further suppressed. As shown in Fig. 6(b), the MOT axial length is 40 mm, and the region for experiments (pumping, probing, etc.) is 400 mm away from the beam-extraction aperture. By adjusting the pushing-beam diameter to 30 mm and placing a lens (f = 400 mm) 400 mm before the aperture, the beam diameter within the MOT region would be still as small as the one (3 mm) in Fig. 3. With the power 10 μW, the pushing laser intensity within the MOT would be almost unchanged. Thus, the pushing rate and the atomic flux are not affected. However, according to the law of geometrical optics, the leaking laser intensity in the experimental region would be reduced to about 1.4 μW/cm². Consequently, the light shift can be further decreased to about −200 Hz, about 100 times smaller than the value −19.76 kHz above. With the pushing power fluctuation suppressed by −50 dB,^[39] the relative frequency uncertainty of an atomic clock based on this 2D-HP beam due to the light shift would be around 1 × 10⁻¹³.

In this work, we present a new design for a source of cold cesium atoms, the 2D-HP MOT. With independent axial cooling and pushing, the 2D-HP MOT can substantially optimize the atomic flux. The atomic flux maximum obtained in the 2D-HP MOT is 4.02 × 10¹⁰ atoms/s, 60% higher than the traditional 2D⁺ MOT. With proper pushing parameters, the 2D-HP MOT can generate a rather intense cold atomic beam with the concomitant light shift 20 times smaller than that in the traditional 2D⁺ MOT. Compared to the traditional 2D⁺ MOT, the 2D-HP MOT needs some more facilities to provide the hollow beam and the pushing beam. But with the total atomic flux increased and the light shift suppressed, it can help improve the precision measurement experiments on cold atomic beams, for example, an atomic clock based on a continuous cold cesium atomic beam.