Room-temperature Si-based light source is one of the most important components of Si-based photonic integration. In recent years, although many developments have been achieved for Si-based light emission,^[1] to overcome the inefficient band-to-band radiative recombination of Si remains a challenge. In the last decade, due to the compatibility with CMOS processes, Ge on Si substrate has been widely studied for Si-based optoelectronic device applications.^[2] Unlike Si, Ge has a direct bandgap only slightly larger (by 140 meV) than its indirect bandgap. The direct optical transition in Ge is a very fast process with a radiative recombination rate four orders of magnitude higher than that of the indirect transitions.^[3] This pseudo-direct bandgap structure allows Ge to be a promising candidate for light emission. The key to improving Ge emitting is to increase electron occupancy in the Γ valley of the conduction band. There are several approaches to achieve this goal, such as tensile strain,^[4,5] high n-doping,^[6] and high injection.^[7] Based on this principle, direct-gap transitions from Ge have been observed by photoluminescence,^[6] electroluminescence,^[7] optical gain,^[8] and even by a Ge laser working at room temperature.^[9,10] On the theoretical side, light emission and optical gain of Ge have been studied comprehensively by different models.^[8,11,12] However, most theoretical studies concentrated on the light emission and optical gain of Ge under tensile strain and heavy n-doping at room temperature. The heating effects in Ge were ignored. Although light emission enhancement of Ge at high temperature was observed,^[6,13,14] the temperature-dependent emission and optical gain of Ge have not been studied in detail.

In this work, we theoretically studied the band structure, electron distribution, direct-bandgap light emission, and optical gain of tensile strained, n-doped Ge at different temperatures. Our result indicated that the heating effects can increase the electron occupancy rate (Γ valley), light emission, and optical gain of Ge at a limited temperature range. We also discussed the free-carrier absorption (FCA) and net optical gain of tensile strained, n-doped Ge on Si.

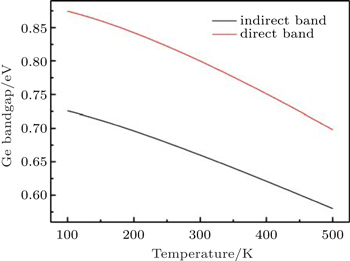
The indirect bandgap and direct bandgap of Ge will both shrink with increasing temperature. Each bandgap has a different shrink rate. The temperature dependences of the indirect bandgap and direct bandgap of Ge are expressed as^[15]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Indirect and direct bandgaps of bulk Ge at different temperatures.

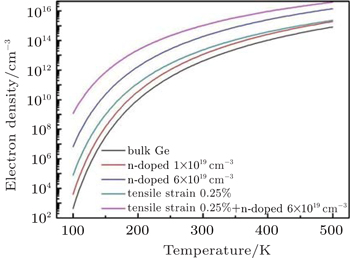
As the band structure of Ge is changed by the heating effects, the carrier distribution in the band is also changed. The electrons and the holes obey quasi-Fermi distributions with respect to the electron quasi-Fermi level (E_Fc) and the hole quasi-Fermi level (E_Fv). The occupation probabilities of an electron and a heavy hole are described by

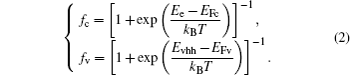
Unlike light emission from direct bandgap materials, the emission from Ge is interrelated only with the electron concentration in the Γ valley. According to Eq. (2), the electron densities in the Γ valley of tensile strained, n-type doping Ge at various temperatures with the input carrier concentration n = p = 1 × 10¹⁹ cm⁻³ are shown in Fig. 2. The band edge diagram of the tensile strained Ge was calculated using the deformation potentials theory.^[17] The number of electrons in the Γ valley increases as the temperature, n-doping concentration, and tensile strain increase. We find that the numbers of electrons in the Γ valley of bulk Ge and 0.25% tensile strained, n-doped (6 × 10¹⁹ cm⁻³) Ge at 500 K are about 200 and 40 times larger than those at 300 K, respectively. Although the electron concentration in the Γ valley can be increased by using these methods, the electron ratio in the Γ valley is still low because of the energy difference between the Γ valley and the L valley and the larger electron state density of the L valley (high degeneracy). For 0.25% tensile strained n-doped (6 × 10¹⁹ cm⁻³) Ge, the electron ratio in the Γ valley is only about 0.01% and 0.4% at 300 K and 500 K, respectively. Such a low proportion of the electrons in the Γ valley is the primary problem that prevents Ge from obtaining efficient light emission.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Electron densities in the Γ valley of different tensile strained, n-doped Ge samples at different temperatures. The input carrier concentration n = p = 1 × 1019 cm− 3.

The emission of Ge is almost proportional to its spontaneous emission rate. Therefore, the total spontaneous emission intensity was used to study the emission intensity of Ge. For a given carrier concentration, the spontaneous emission rate of electrons in the Γ valley to the heavy hole band can be calculated according to the expression^[18]

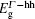
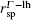
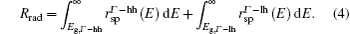
According to Eqs. (3) and (4), the light emission intensities of various n-doped Ge at different temperatures with the input carrier concentration n = p = 1 × 10¹⁹ cm⁻³ are shown in Fig. 3. The light emission intensity exponentially increases with increasing temperature. The light emission intensities of 5 × 10¹⁸ cm⁻³ n-doped Ge and 1 × 10¹⁹ cm⁻³ n-doped Ge are about 1.8 and 2.8 times larger than those of undoped Ge at 300 K, which agrees with a previous experimental report.^[19] The light emission intensity of Ge with a lower n-doping concentration is more sensitive to the temperature. The light emission intensities of undoped Ge and 6 × 10¹⁹ cm⁻³ n-doped Ge at 500 K are about 10 and 3.6 times larger than those at 300 K, respectively. This phenomenon indicates that, the light emission characteristics of heavy n-doped Ge are similar to those of the direct bandgap material. However, heavy n-doping cannot change Ge to be a direct bandgap semiconductor.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Light emission intensities of various n-doped Ge at different temperatures. The input carrier concentration n = p = 1 × 1019 cm−3.

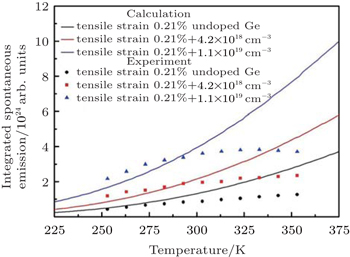
To verify the calculation results, temperature dependent photoluminescence measurements of three 0.21% tensile strain Ge films on Si with various n-doping (undoped, 4.2 × 10¹⁸ cm⁻³ n-doped, and 1.1 × 10¹⁹ cm⁻³ n-doped) were performed from 253 K to 353 K. The injected carrier density was estimated to be about 1 × 10¹⁹ cm⁻³. The experiment results and calculation results are shown in Fig. 4. When the temperature is lower than 300 K, the experiment results are overall in agreement with the calculation results. This result indicates the accuracy of the theoretical calculations at moderate temperature. When the temperature is higher than 300 K, the experimental light emission intensity does not increase exponentially as the calculated intensity. The light emission intensity of the 1.1 × 10¹⁹ cm⁻³ n-doped Ge film even tends to saturate and decrease. This phenomenon is attributed to non-radiative recombination like the Auger process and FCA induced optical loss, which strengthen at high temperature and heavy doping.^[20,21] Moreover, because of the bandgap narrowing by heavy n-type doping, tensile strain, and the increase of temperature, most of the emission peaks are lower than the low energy cut-off of the InGaAs detector (1600 nm), which also induces the trend of saturate and decrease.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Temperature-dependent photoluminescence intensity and calculational light emission intensity of three 0.21% tensile strained n-doped Ge films on Si from 253 K to 353 K. The injected carrier density is estimated to be about 1 × 1019 cm−3.

Fig. 5.

	Figure Option ViewDownloadNew Window
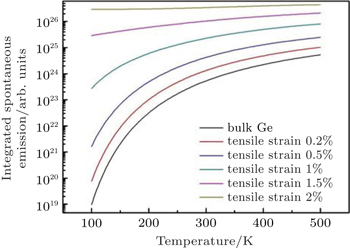	Fig. 5. Light emission intensitits of various tensile strained Ge at different temperatures. The input carrier concentration n = p = 1 × 1019 cm−3.

Figure 5 shows the light emission intensities of various tensile strained Ge at different temperatures with the input carrier concentration n = p = 1 × 10¹⁹ cm⁻³. Like the light n-doped Ge, the light emission intensity of lower tensile strained Ge is more sensitive to the temperature than that of higher tensile strained Ge. The light emission intensities of unstrained Ge and 2% tensile strained Ge at 500 K are about 10 and 1.3 times larger than those at 300 K, respectively. In our calculation, 2% tensile strain can change Ge into a direct bandgap semiconductor, in which the Γ valley is lower than the L valley by about 34 meV. However, unlike common III–V direct bandgap materials, the light emission intensity of this direct bandgap Ge still has a weak positive temperature characteristic. This interesting phenomenon could be explained by the larger electron state density of the Γ valley at higher temperature. The light emission intensities of n-doped 0.1% tensile strained Ge and 0.2% tensile strained Ge are about 1.6 and 2.5 times larger than that of bulk Ge at 300 K, which also agrees with the previous experimental report.^[19] This result also implies the accuracy of our calculations.

Although the electron occupancy rate in the Γ valley of Ge is low, the optical gain of Ge can be obtained in theory. The heavy n-doped Ge film on Si with 0.25% tensile strain is a typical example, which was used in optical gain and laser of Ge.^[9,22] Therefore, we choose this typical example to study the optical gain of Ge at different temperatures. For a given carrier concentration, the gain spectrum of electrons in the Γ valley to the heavy hole band can be calculated according to the expression^[18]

Figure 6 shows the optical gain spectra of 0.25% tensile strain Ge films on Si with 6 × 10¹⁹ cm⁻³ n-doping at various temperatures. The input carrier concentration n = p = 1 × 10¹⁹ cm⁻³. The gain peaks have obvious red-shifts with the increase of the temperature. All gain spectra consist of two gain peaks. The gain peak with the higher energy originates from the Γ–hh process. The small gain peak with the lower energy is due to the Γ–lh process. Although the light hole band is lower than the heavy hole band under tensile strain, most of the holes still occupy the heavy hole band because of the larger electron state density of the heavy hole band. Therefore, most optical gain originates from the Γ–hh process.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Optical gain spectra of 0.25% tensile strained Ge films on Si with 6 × 1019 cm−3 n-doping at various temperatures. The input carrier concentration n = p = 1 × 1019 cm−3.

When the temperature is lower than 300 K, the optical gain of 0.25% tensile strained Ge films on Si with 6 × 10¹⁹ cm⁻³ n-doping has positive temperature characteristics. This result can be explained by the fact that more electrons are thermally excited from the L valley to the Γ valley. When the temperature is higher than 300 K, the optical gain has the negative temperature characteristics, i.e., the optical gain decreases with the increase of the temperature. This phenomenon is attributed to the flatter hole distribution at high temperatures. The heating effects not only smear out the electron distribution and increase the electron occupation in the Γ valley, but also smear out the hole distribution, which prevents obtaining higher optical gain. This carrier distribution flattening is also reflected in the broadening of the gain spectral width. The gain spectral width increases from 125 nm at 200 K to 145 nm at 400 K.

To obtain the net optical gain of Ge, the optical loss induced by FCA should be considered, especially in high doping and high injection case. The FCA consisting of the absorptions of the L valley, the Γ valley, the heavy-hole band, and the light-hole band can be described by the Drude–Lorentz equation as follows:^[21]

According to Eqs. (5)–(7), the maximum gain and the net maximum gain of 0.25% tensile strained Ge films on Si with various n-doping at different temperatures are shown in Fig. 7. The input carrier concentration n = p = 1 × 10¹⁹ cm⁻³. We can find that the FCA increases rapidly with the elevating of the temperature. In this condition, the 0.25% tensile strained Ge films on Si with 7 × 10¹⁹ cm⁻³ n-doping cannot obtain a net optical gain at 300 K. Although the heating effect can increase the electron occupation in the Γ valley, it also increases the FCA. Therefore, to obtain higher net maximum gain, heavy n-doped 0.25% tensile strained Ge films on Si should work at a suitable temperature, which can balance the gain increase by the heating effect and the optical loss induced by the FCA.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Maximum gain and net maximum gain of 0.25% tensile strained Ge films on Si with various n-doping at different temperatures. The input carrier concentration n = p = 1 × 1019 cm−3.

We theoretically studied the band structure, electron distribution, direct-bandgap light emission, and optical gain of tensile strained, n-doped Ge at different temperatures. We found that the heating effects affect the light emission and optical gain of Ge in three aspects. Firstly, like tensile strain, the heating effects reduce the energy difference between the Γ valley and the L valley. This brings benefits to the light emission and optical gain of Ge. Secondly, the heating effects increase the electron occupancy rate in the Γ valley of Ge by Femi-level flattening (thermal excitation). The Femi-level flattening increases the light emission of Ge, but decreases the optical gain of Ge, when the hole and electron distributions become more flat at high temperatures. Thirdly, the heating effects increase the optical loss induced by FCA. Intensive FCA is one of the main reasons for the deterioration of the net optical gain of Ge at high temperatures. Therefore, to obtain high net maximum gain, tensile strained, n-doped Ge films on Si should balance the gain increase by the heating effect and the optical loss induced by the free-carrier absorption. This work helps to elucidate the mechanism of positive temperature characteristics of Ge light emission, and is useful for designing Ge light emitters and lasers.