† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11447178).
Starting from the Hamiltonian of the second quantization form, the weakly interacting Bose–Einstein condensate with spin–orbit coupling of Weyl type is investigated. It is found that the SU(2) nonsymmetric term, i.e., the spin-dependent interaction, can lift the degeneracy of the ground states with respect to the z component of the total angular momentum Jz, casting the ground condensate state into a configuration of zero Jz. This ground state density profile can also be affirmed by minimizing the full Gross–Pitaevskii energy functional. The spin texture of the zero Jz state indicates that it is a knot structure, whose fundamental group is π3(M) ≅ π3(S2) = Z.
It is well known that the Bose–Einstein condensate (BEC) supplies us with nearly an ideal platform to investigate quantum phenomena with the help of lasers and magnetic fields. For example, the interactions between atoms can be manipulated by changing the strength of an applied magnetic or electric field for species that have a Feshbach resonance.
In 2008, Wu et al. theoretically explored the isotropic Rashba spin–orbit coupled Bose–Einstein condensation and spin–spiral-type condensate, and a half-quantum vortex was observed.[1] In 2009, artificial external gauge potentials coupled to neutral atoms were generated by controlling atom-light interaction.[2] Due to the presence of the spin–orbit coupling mechanism, the energy spectrum changes dramatically. The single particle energy minimum has finite momentum and the ground states are circularly degenerate, in which case the ground state of the condensate favors mainly the “stripe” or “plane wave” phase.[3–5] Therefore, spin–orbit coupled cold atom systems have attracted intensive attention over the last few years,[6–18] such as the studies on topics of Spin Hall effects,[19] Majorana fermions,[20,21] etc. Xu et al. theoretically investigated the interesting density patterns of the spin–orbit coupled spinor condensate in the presence of rotation.[22–24] It was found that the condensate may become self-trapped as a result of the spin–orbit coupling and the nonlinearity, resembling the so-called chiral confinement.[25] Zhang et al. found that the condensate with spin–orbit coupling exhibited dynamical oscillations similar to the Zitterbewegung oscillation.[26] Deng et al. also investigated the spin–orbit coupled condensate in the presence of the dipole–dipole interactions.[27] For a weakly interacting bosons system, the spin–orbit coupled condensate favors a ground state with a zero or finite z component of the total angular momentum.[28,29]
For the spin–orbit coupled condensate of three dimensions, Anderson and Clark investigated the single-particle characteristics and found that the system showed a dimensional reduction from three to one and the single-particle spectrum could be well approximated by Landau levels in the radial coordinate and the splittings were inversely proportional to the spin–orbit coupling strength. Kawakami et al. found that the three-dimensional skyrmion appeared as the ground state of SU(2) symmetric BECs coupled with a non-Abelian gauge field.[30] Li et al. found that the topology of condensate wavefunctions manifested in the quaternionic representation.[31] The spatial distributions of the quaternionic phase show three-dimensional skyrmion configurations, and non-zero Hopf invariants of topological objects in S2 spin orientation was also observed. Recently, Liu and Yang from Beijing Normal University observed the novel topological object three-dimensional dimeron in trapped two-component BECs and explored both exact static and moving solitonic solutions in F = 1 BECs.[32,33] However, the SU(2) nonsymmetric BEC with three-dimensional spin–orbit coupling of Weyl type has not been definitely investigated as far as we know. Among the factors which would determine the nontrivial ground states, what role does the spin-dependent interaction play?
In the present paper, we investigate the weakly interacting two-component condensate with three-dimensional spin-orbit coupling of Weyl type. It is found that finite spin-dependent interaction drives the condensate into zero total angular momentum (Jz = 0) ground state. Numerically minimizing the full Gross–Pitaevskii energy functional, the state with only spin-dependent interaction favors a knot structure, whose topological Hopf charge is QH = 1. The paper is organized as follows. In Section 2, we show the single-particle energy spectrum and the eignstates as well. In Section 3, the ground state with weak interaction is investigated within the basis vectors obtained in Section 2. In addition, the imaginary time evolution method is also exploited to confirm the numerical results. Finally, a summary is presented in Section 4.
We begin with the single-particle Hamiltonian
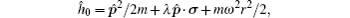
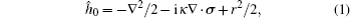
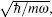

Because of the spin–orbit coupling, the orbital angular momentum is not conserved any more. The total angular momentum 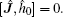
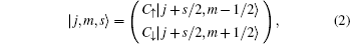
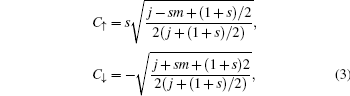
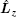
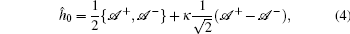
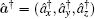
Next, the basis vectors can be constructed by considering the quantum number n in the radial direction,
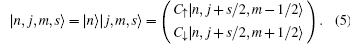

Since both
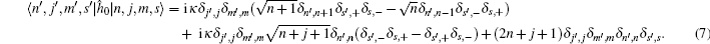
In the presence of the spin-dependent and spin-independent interactions, the model Hamiltonian in the second quantization form is given by


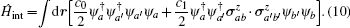
For a weakly interacting N-boson system, only several lowest energy levels are occupied. Thus, the field operator can be expanded as Ψ =



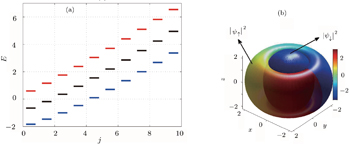
According to the single-particle spectrum in Fig.
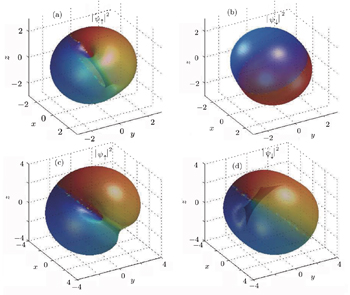
In the absence of the spin-dependent interaction, the ground states with Jz = 0 and Jz ≠ 0 are degenerate. That means the states with Jz = 0 and Jz ≠ 0 have identical total energy. However, in the presence of the spin-dependent interaction, the condensate is cast into a zero Jz = 0 state. Figures
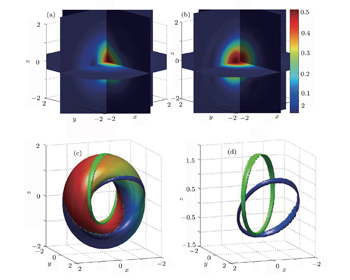
A similar conclusion can also be drawn by minimizing the full Gross–Pitaevskii energy functional realized by promoting the imaginary evolution of the following Gross–Pitaevskii equations[34–37]
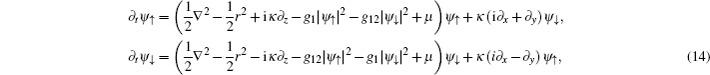
Figures
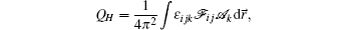


In summary, we have investigated the weakly interacting two-component BEC with three-dimensional spin–orbit coupling of Weyl type. The role of the SU(2) nonsymmetric term, i.e., the spin-dependent interaction, is clarified. It is found that the finite spin-dependent interaction drives the condensate into Jz = 0 ground state. The mean-field numerical results show that the ground state shows a knot spin texture whose topological charge is QH = 1. This should help us to clarify the effect of the spin-dependent interaction in the process of the cold atom simulation. In addition, the results may shed light on the research of the topological nontrivial objects in cold atom systems.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 |