Cite this Article
Cao Si-Qin, Wei Guang-Hong, Chen Jeff Z. Y.‡. Bending energy of a vesicle to which a small spherical particle adhere: An analytical study. Chinese Physics B, 24(9): 098702  
Permissions
Bending energy of a vesicle to which a small spherical particle adhere: An analytical study
Cao Si-Qina), Wei Guang-Honga), Chen Jeff Z. Y.‡b)
State Key Laboratory of Surface Physics, Key Laboratory for Computational Physical Sciences (Ministry of Education), Department of Physics, Fudan University, Shanghai 200433, China
Department of Physics and Astronomy, University of Waterloo, Ontario N2L3G1, Canada

†Corresponding author. E-mail: ghwei@fudan.edu.cn

‡Corresponding author. E-mail: jeffchen@uwaterloo.ca

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11074047 and 11274075), the Research Fund for the Doctoral Program of Higher Education of China (Grant No. RFDP-20100071110006), and the Natural Science and Science Engineering Council of Canada.

Abstract

On the basis of Helfrich’s bending energy model, we show that the adsorption process of a small spherical particle to a closed vesicle can be analytically studied by retaining the leading terms in an expansion of the shape equation. Our general derivation predicts the optimal binding sites on a vesicle, where the local membrane shape of the binding site could be non-axisymmetric before the continuous adhesion transition takes place. Our derivation avoids directly solving the shape equation and depends on an integration of the contact-line condition. The results are verified by several examples of independent numerical solutions.

PACS: 87.16.dt; 46.70.Hg; 68.03.Cd; 87.17.Aa
Keyword: membrane conformation; Helfrich model; nano-particle adsorption; phase transition
1. Introduction

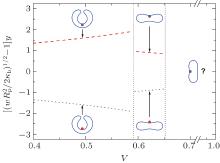
The theoretical treatment of a membrane, either in an open conformation or in a closed vesicle conformation, is largely based on the bending-energy model that was originally proposed by Helfrich.[1] Insightful structures can be theoretically determined from this model, which are then used to describe experimental observations in membrane systems.[2, 3] For example, free-vesicle shapes can be predicted from the model. In particular, those having an axisymmetry have been classified as a function of the vesicle’ s reduced volume

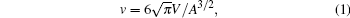
where V is the internal volume and A is the surface area of a vesicle.[2, 4, 5] Three representative conformations (i.e., stomatocyte, oblate, and prolate) are illustrated in Fig.  1.

Fig.  1. Three representative conformations of a vesicle: a v= 0.4 stomatocyte (a), a v= 0.6 oblate (b), and a v= 0.8 prolate (c). According to the current work, the internal and the external adhesion sites are indicated by (red) circles and (green) squares, respectively, for a small spherical particle adhering to a stomatocyte (a), an oblate (b), and a prolate (c). The filled diamonds specify the equatorial line on a prolate that is further discussed in Section  3.5.

As an approximation, synthetic nano-particles and viruses that interact with a membrane surface are commonly modeled by a hard spherical particle.[6– 8] In this paper, we examine the structure of a particle– membrane complex caused by particle– membrane adhesion. This adhesion is usually characterized by an attraction energy per unit area, w, acting between the particle and membrane surface on contact.[9] One important theoretical identity is the contact-line condition that connects the local membrane and substrate curvatures at the contact line to the adhesion strength w, [10] in a general form regardless of the original membrane shape and adhering particle geometry. This identity will be employed in Section  3.2 of the current work. The model system of a spherical particle adsorbing to a flat, deformable, and infinitely large membrane sheet was previously considered in order to illustrate many interesting concepts, such as the continuous adhesion transition and engulfing of the sphere by the membrane as w raises.[11– 14]

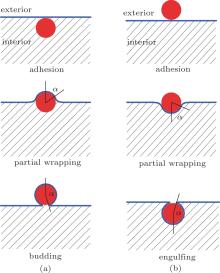
The physical properties of the adhesion of a spherical particle to a vesicle has been explored by using computer simulations of a coarse-grained model, [15] and variational and numerical calculations of the bending energy model.[16– 20] As it turns out, for an oblate vesicle, as w and the size of the adhering sphere change, an exact numerical solution to the bending energy model yields a rather rich phase diagram where multiple phases exist.[17] Adhesion of a small sphere to the internal surface would result in budding as w increases [Fig.  2(a)], or adhesion to the external surface would result in engulfing as w increases [Fig.  2(b)]. Within the length scale of an adhering sphere, the membrane appears large, thus locally these processes do not differ much from the simple picture of a sphere adhering to a flat membrane, [11– 14] where the transition properties are controlled by a surface tension σ . Here, we focus on a system where the vesicle has a size which is much greater than the adhering sphere’ s radius. The adhesion site depends on the curvature of the vesicle where the small sphere approaches, which in turn influences the onset of the adhesion transition. As will be shown below, for such a problem, σ is no longer important.

Fig.  2. (a) Conformations in a budding transition: adhesion of a sphere to the membrane from the interior of a vesicle, sphere partially wrapped by the membrane, and a budding state where the sphere is entirely wrapped by the membrane; (b) conformations in an engulfing transition: adhesion of a sphere to the membrane from the exterior of a vesicle, sphere partially wrapped by the membrane, and engulfing of the sphere by the membrane.

This paper is organized as follows. In Section  2, we adopt a general form of the bending energy model and will briefly review the resulting shape equation that governs curvature properties of the membrane.[23– 26] In Section  3.1, with the consideration of a small adhering sphere, we argue that near the contact line the membrane displays a catenoid shape; regardless of the global, possibly non-axisymmetric vesicle shape, locally a symmetry axis can be chosen for the wrapping membrane on the small sphere. Some detailed mathematical derivations that back up the argument can be found in Appendices. In Appendix A, we set up a general coordinate system for the problem. In Appendix B, we expand the shape equation in terms of a small parameter, which does not depend on an axisymmetry coordinate setup that was used previously.[11– 14, 16, 17, 27, 28] The result is an analytic expression for the membrane curvature at the contact line, which is presented in Section  3.1. In Appendix C, we show that the contact line on a small sphere is a circle. In Section  3.3, using the general contact-line condition, we analytically determine the bending energy of the non-adhering vesicle portion of a partially wrapped sphere-vesicle complex, the energy depends on the curvature of the initial adhesion site. According to these results, in Sections  3.4 and 3.5, we locate the adsorption sites for the adhesion– budding transition and adhesion– engulfing transition on a vesicle; some examples are specified in Fig.  1 by circles and squares. The numerical solution to the original free vesicle problem is then used to determine the adhesion phase transition and deep wrapping (budding and engulfing) boundaries in two examples. Our general analytic results, which are based on the approximation of a small particle radius, are validated in Sections  3.3 and 3.6 by comparing them with independent numerical solutions to the same problem without taking the approximation.[17]

2. Model

The total energy of the particle– membrane complex is composed of the membrane’ s bending energy, Eb, surface tension, and work of the osmotic pressure, Es, as well as the particle– membrane interaction energy, Ea. The bending energy of the membrane is generally described by the curvature model[1– 3]

where K/2 = (C1+ C2)/2 is the mean curvature, G = C1C2 is the Gaussian curvature, and C1 and C2 are the two principle curvatures of the membrane surface element d A. We consider the general case of a nonvanishing spontaneous curvature, C0; for a symmetric bilayer lipid composition we set C0 = 0 later.[29] The two bending moduli, κ b and κ G, together with C0, are system dependent.

We consider the particle– vesicle adhesion interaction that does not yield any vesicle topological change. According to the Gauss– Bonnet theorem the last term in Eq.  (2) is a constant. Instead of dropping that term, we explicitly keep it for consistency in the derivation given below. Normally, one assumes that the total surface area and the internal volume of the vesicle are fixed for a particular system. A mathematically equivalent treatment is given by the introduction of two Lagrangian multipliers, σ and p, to deal with the constraints. This amounts to an additional energy

which has the physical meaning of surface-stretching energy and osmotic-pressure based work.

The adhesion energy is assumed to be proportional to the contact area AC (i.e., the area of the spherical particle that is covered by the adhering membrane)

where w is the attraction energy gain per unit area between the membrane and the particle’ s surface. A similar expression has been used in recent studies of related systems.[5, 10, 16, 17, 21, 22, 30– 36] This energy becomes effective when the surfaces of the particle and membrane are in contact. Alternatively, one could use a potential-well based attraction scheme, such as those normally used in computer simulations, [21, 22, 37, 38] where the attraction energy is a function of the distance between the surfaces. In the current approach, we use the more convenient contact attraction in Eq.  (4) with the understanding that the two approaches are physically the same for a short-ranged potential well.

One can then take the sum of the above three energies and treat the problem by a variation method to minimize the total energy in order to determine the optimal vesicle shape. The shape of the free portion of the membrane is then described by the differential equation[23– 26]

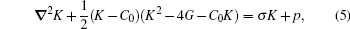
where ∇ 2 is the Laplacian operator.

3. Results and discussion
3.1. Membrane’ s curvature at the contact line of a small adsorbing sphere

In this subsection, we consider the contact line shape for adhesion to a small spherical particle having a radius Rp. When we say a “ small” particle, we refer to the condition

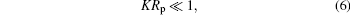
where K/2 is the mean curvature on any point of the nonadhered portion of the vesicle.

Fig.  3. An arbitrary contact line on the surface of a sphere where part of the sphere is partially wrapped by the (blue) membrane.

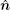
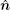
The contact line forms a loop (of an arbitrary shape for now) on the surface of the (red) sphere, as shown in Fig.  3. At any point X on the contact line: a unit vector tangent to the contact line specifies the parallel (∥ ) direction, ê ∥ ; a unit vector normal to the plane locally tangent to both membrane and adsorbing hard surfaces at X specifies the surface normal, ; and finally, a unit vector normal to both ê ∥ and specifies ê ⊥ .

According to differential geometry two curvatures, K⊥ and K∥ , can be defined along ê ⊥ and ê ∥ . The mean curvature K/2 can then be expressed through

As already discussed in Refs.  [10] and [39], crossing the contact line by following the ê ⊥ direction, K⊥ is discontinuous from the unadsorbed membrane portion to the adsorbed portion. On the other hand, crossing X following the contact curve, K∥ , is continuous.

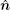
The surface normal of the adsorbing sphere at X is the same as the radial direction , directing from the center of the sphere to X. Because at X is a joint surface normal for both the membrane and substrate surfaces

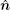
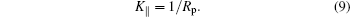
Therefore, and ê ∥ defines a great circle on the spherical surface, from which we have

This is actually true for any Rp size.

Now consider the unadsorbed side of the membrane emerging from X. Taking Eqs.  (7) and (9), we have

In the current small sphere system, from Eq.  (6), we can drop the RpK term, hence K⊥ ≃ − K∥ = − 1/Rp. This implies that the membrane shape at the contact line is a catenoid surface. A few interesting features immediately emerge.

First, K∥ = 1/Rp is a constant along the entire contact line. This property, together with an asymptotic solution of Eq.  (5) in the small-Rp limit, guarantees that the contact line is a circle on the particle’ s surface [see Appendices  A, B, and C]. Although the parametrization so far is for a general, non-axisymmetric case, this means that a new, local z axis can be established, about which the membrane near the contact line is axisymmetric. At a larger scale, the entire vesicle shape need not be axisymmetric.

Next, following such a local axisymmetric setup, the location of the contact circle on the sphere is uniquely defined by the parameter θ , from which α = π -θ can now be interpreted as the wrapping angle on a spherical adsorbing substrate. In Appendix B, solving Eq.  (5) we show that the membrane curvature K at the contact line follows:

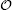
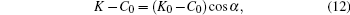
where A is a constant that does not depend on the wrapping angle. The terms that were neglected have the order of magnitude (RpK2). The constant A can be determined by considering the special case, α = 0, which gives A = K0 − C0, where K0 is the curvature when the membrane just touches the adsorbing sphere at a vanishing wrapping angle. In this work, we focus on the case that the adhesion transition is continuous, which implies that K changes continuously before and after the adhesion transition taking place at α = 0. Hence, we can write

where K0 can be understood as the curvature of the membrane before the particle is adhered. This curvature, of course, depends on the location on the vesicle that the particle adheres to.

3.2. Contact-line condition

The contact-line condition

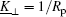
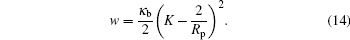
relates the adsorption energy w to K⊥ of the membrane on the two sides of the contact line, K⊥ on the unadsorbed side and on the adsorbed side. The relationship was derived by Seifert and Lipowsky[10] as well as Deserno.[39] For an adsorbing sphere, . Using K⊥ ≡ K − K∥ = K − 1/Rp we have

So far, this condition is for any size of adsorbing sphere. Taking the small sphere result, equation  (12), we then have

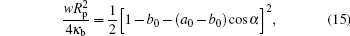
where a0 = K0Rp/2 and b0 = C0Rp/2.

3.3. Bending energy of the vesicle– particle complex

Now, we consider a variation process where the contact area AC between the membrane and particle varies, and the bending energy δ Eb changes due to the vesicle distortion caused by adhesion. The total energy must remain minimum

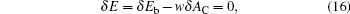
which is an condition that was considered previously.[10, 39] This expression can be used as the basis for arriving at a general procedure of calculating the bending energy Eb (AC). By integrating this expression, we have

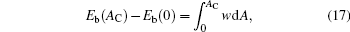
where Eb(0) is the original vesicle energy before the adsorption takes place.

The integrand in the above, w, is already given in Eq.  (15) as a function of α . Considering the relationship between A and α

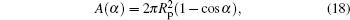
we can carry out the integral and obtain

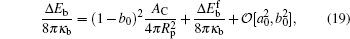
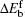
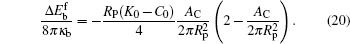
where Δ Eb = Eb(AC) − Eb(0) is the difference between the bending energy of the particle– membrane complex and the vesicle energy before the adsorption. The first term on the right-hand side of Eq.  (19) is the membrane’ s bending energy associated with the contact area AC and the second term is the energy of the unattached potion of the vesicle, , where

Valid for small-particle adsorption, the bending energy difference, equation  (19), was obtained without the explicit consideration of calculating the membrane shape curve, which has been done previously.[5, 10, 16, 17, 30– 36] Note that a0, through K0, is adhesion-site specific. This general expression is suitable for any adhesion site on the vesicle, where the site could be a locally non-axisymmetric point. Another interesting point is that the Lagrangian multipliers σ and p that were introduced in the earlier stage of the theory have now disappeared in the final result. This surprising conclusion can be traced back to solving Eq.  (5): by taking a small Rp limit, the terms associated with σ and p disappear in an order-of-magnitude estimation, as presented in Appendix  B. The net effects of σ and p on the original problem of the considered vesicle (before particle adhesion) still remain and they determine the stable free vesicle shape.[2, 5]

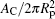
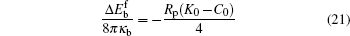
Equation  (20) is a remarkable analytic result, which states that the bending energy of the unattached portion is a quadratic function of the reduced contact area , having a maximum magnitude

at half wrapping when 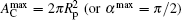. The sign of this energy is completely determined by the sign of K0− C0.

To validate this result, we consider two examples, both having C0 = 0. As previously known, the free vesicle shape is completely controlled by a dimensional characteristic number of the vesicle, the reduced volume in Eq.  (1). We considered two special cases, v = 0.6 and v = 0.95, corresponding to an oblate vesicle and a prolate vesicle, respectively. We have solved the adsorption problem following the numerical procedure described in our previous paper, [17] without any of the analytic consideration explained above. 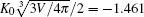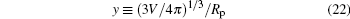The adsorption sites for both cases were selected at the axisymmetric axis of the vesicle (the “ north pole” ), where and , respectively, for the two cases, v = 0.6 and v = 0.95. For each case, three values of the dimension ratio

are considered in the numerical solution.

The parameter y measures the relative size of the vesicle in comparison with the radius of the adsorbing spheres. We expect that asymptotically large y data converge to our theoretical prediction. In Fig.  4, we plot the numerical data by triangles (y = 21.5), squares (y = 36.8), and circles (y = 46.4). The two examples, v = 0.6 and v = 0.95, are shown by filled and open symbols in the figure. As the particle’ s radius is reduced (or y increases), we can see that the numerical results converge to the theoretical curves for small Rp, equation  (20), plotted as the solid curve for v = 0.95 and dashed curve for v = 0.6.

Fig.  4. Comparison between the numerical results (symbols) and the theoretical prediction (lines) of the bending energy change for the unattached membrane portion, 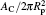, as a function of the reduced wrapping area, . Two example vesicles are considered: v = 0.6 (filled symbols) and v = 0.95 (open symbols). The numerical results were obtained by solving the shape equation exactly; [17] the theoretical prediction, equation  (19), is made by an expansion on the small particle radius. Triangles, squares, and circles correspond to vesicle to particle dimension ratio, y = 21.5, 36.8, and 46.4, respectively. The dotted horizontal lines represent a typical thermal energy of order kBT, whereas the bending modulus κ b is taken here to be ≈ 10 kBT (the value of POPC reported in Ref.  [40]); for different y the same color is used here.

We have demonstrated here that our exact solution can be validated by the numerical solution, which are both obtained on the assumption that the thermal fluctuations can be ignored. An interesting question is: how useful is the plot in this figure in comparison with a real system where the thermal fluctuations exist? A typical thermal energy KBT can be compared with κ b by κ b ∼ 10 KBT. In Fig.  4, we illustrate the typical thermal energy by dotted lines. In most of the parameter region, our theoretical expression should be unaffected by thermal fluctuations.

3.4. Internal adhesion and budding transition

We first discuss the predicted physics of internal adhesion, which eventually results in the budding of a small particle to the interior wall of a vesicle, using the derivation in the above sections. For simplicity, we only consider membranes without spontaneous curvature, C0 = 0. Before adhesion, the vesicle is in a free vesicle state, which is a problem that was previously studied by Seifert et al.[15] according to the bending energy model, Eq.  (2). The stable structure depends on a single geometric parameter. In the reduced volume v in Eq.  (1), the stomatocyte is stable within the range v = (0, 0.5915], oblate v = [0.5915, 0.6516], and prolate v = [0.6516, 1]. Figure  1, without the additional marked symbols, illustrates the shape of these structures at v = 0.4, 0.6, and 0.8.

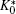
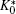
Note that K0 is defined from the adhering particle side. For the current case, it differs by a sign from the case where the particle adheres from the exterior of the vesicle. At the beginning of the adhesion transition, the contact area AC is asymptotically small. To minimize the energy in Eq.  (20), the particle seeks an interior site where K0 is concave and has the maximal curvature . A few examples of the curvature of the unperturbed vesicle, K0, are illustrated in Appendix  D, where is indicated by a red dot. This identifies the preferred internal adhesion sites, labeled by (red) circles in Fig.  1. In both stomatocyte (v = 0.4) and oblate (v = 0.6), the adhesion sites form a circle about the overall-shape symmetric axis. The local sites are not axisymmetric before adhesion takes place. In a cross section view of a stomatocyte, the most concave points appear at a place with C1 is maximum, which is different from the actual place where K0 = C1+ C2 is the maximum.

The continuous internal adhesion transition can then be determined by letting the wrapping angle α → 0 in Eq.  (2). By re-arranging the quantities, we obtain the transition adhesion energy, wad, in

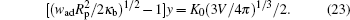
The quantities in this expression have been arranged so that the right hand side does not contain the particle size Rp. The dimensionless K0V1/3 can be calculated from a numerical solution to the free vesicle problem[5, 17] and is plotted in Fig.  5 by the dotted curve. Below wad the system is in a desorbed state, while above wad the system is in a partially wrapped state. At the onset of the transition when w = wad, the vesicle shape changes continuously from those plotted in the figure to enable a non-trivial wrapping angle.

As w increases beyond wad, more of the area of the sphere is covered by the wrapping membrane, until the wrapping area reaches the full wrapping value, 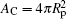, at which α = π . In this particular case, the small sphere is completely wrapped, forming a bud at the adhesion site. The same Eq.    (15) can be used to determine the onset of the budding transition by setting α = π

Note that the right hand side of this equation has a sign difference from Eq.  (23). The conformation of a budding particle– membrane complex can be recovered from the analytic analysis. Because of the small volume Vp, the nonadhered portion of the vesicle has a volume V′ = V − Vp≃ V and a surface area A′ = A − Ap≃ A. Given the fact that the shape curve now closes with a wrapping angle α = π , the nonadhered vesicle portion has an identical shape as the original, free vesicle. Some example configurations are illustrated in Fig.  5 near the budding boundary, wbud, which is represented by the dashed curve.

Fig.  5. The adhesion– budding phase boundaries analytically determined in the current work. The dotted line divides the desorbed state and adhesion state, according to Eq.  (23). The dashed line divides the adhesion state and the budding state, according to Eq.  (24).

3.5. External adhesion to vesicle and engulfing transition

In this section, we discuss the consequences of applying Eq.  (19) to the case of external adhesion of a small adhering spherical particle to the outside layer of a vesicle. For simplicity, we again focus on the case of no spontaneous curvature, C0 = 0 [or b0 = 0 in Eq.  (19)].

The optimal adhesion site on the vesicle can then be predicted based on Eq.  (19) for both a stomatocyte or oblate. Because K0, hence a0 in Eq.  (19) is site-dependent, and we can search for the most concave (K0> 0) site where K0 is a maximum. The (green) squares in Fig.  1 specify these sites for these two typical cases.

Here, we assume that the adhesion transition is continuous such that at the transition α starts from 0. Using α = 0 in Eq.  (15) we can then predict that the adhesion transition takes place as w increases to wad, where wad is given in  Eq.  (23). The dotted curve in Fig.  6 illustrates this phase boundary.

Fig.  6. The adhering– engulfing phase boundaries analytically determined in this work. The dotted line separates the desorbed and adhesion states, while the dashed line separates the adhesion and engulfing states. The phase behavior in the prolate region is unknown from the current work.

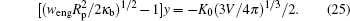
As w goes beyond wad, the sphere starts to become partially wrapped by the membrane. The fully wrapped, i.e., engulfing state, is reached when AC becomes , or α = π for a small spherical particle. The onset of engulfing, weng, can be determined from the same equation as in Eq.  (24)

The long-dashed curve in Fig.  6 indicates the engulfing boundary. For a small sphere, Vp ≪ V and Ap ≪ A, the much larger portion of the newly closed vesicle forms a conformation that is identical to the original free vesicle shape, as illustrated by the conformation in the same figure near the engulfing boundary.

We assumed that the initial adhesion transition is continuous, which has been demonstrated in a number of related systems where the numerical and analytical solutions to the bending energy model were obtained.[10, 16, 17, 30– 36] In all of these cases, including those discussed in the last section and the two examples (stomatocyte and oblate) cited above, the adhesion sites on the original vesicle are either concave or flat, as approached from the adhesion side.

The analysis, however, becomes problematic when generalized to the case of small particle adhesion to a prolate (Fig.  1). Although some regions of the prolate shape curve look concave in the cross section view, figure  1, the entire three-dimensional vesicle shape is actually convex (K0< 0). According to Eq.  (19), we would conclude that the adhesion transition takes place at a site where − K0 is minimal, or |K0| is the smallest. The “ equator” line on the prolate, as illustrated in Fig.  1 by two diamonds, is the location qualifying the requirement. Taking it further, we would also predict that engulfing takes places at a value specified by Eq.  (25). Because K0< 0, according to Eqs.  (23) and (25), weng < wad, in a reversed order in comparison with the examples discussed above. Hence, as w increases, the system would first undergo a discontinuous engulfing transition and then the wrapping angle would decrease as w increases. This rather unphysical consequence is not self-consistent with the basic assumption used in our theoretical analysis, which states that a continuous adhesion transition is followed by engulfing at a larger w. Hence, we cannot directly use the current theory for the prolate desorption– adhesion– engulfing transitions.

3.6. Comparison with the numerical solution

The main theoretical results in this work, equations  (15) and (19), were analytically derived based on: (i) a small-Rp expansion of the shape equation [Eq.  (11)], (ii) the contact line condition [Eq.  (13)], and (iii) the assumption that the adhesion transition is continuous. For the problem of particle adhesion to a vesicle with an axisymmetry, we can solve the original problem numerically without these assumptions, independent of any derivation in this paper, starting from the same bending energy model.[17] A comparison between the current analytical results and the independent numerical results would validate both approaches, particularly (i)– (iii) given above.

Using the computational method documented in our previous publication, we can draw the phase boundary completely on the basis of numerically comparing the magnitude of the calculated total energy of the system at different w for various Rp. One example is for an oblate, v = 0.6, for which the continuous adhesion boundary and engulfing boundary were previously determined[17] and is redrawn in Fig.  7 by squares and circles, respectively. Also shown are the adhesion (dotted) and engulfing (dashed) lines determined from the current analytic approach. There is an excellent agreement between the results from the two, approaching the large V/Vp limit.

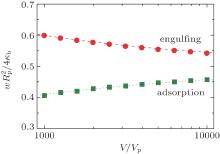Fig.  7. Comparison between the theoretical adsorption and engulfing boundaries Eq.  (15) (b0 = 0, θ = 0) and the numerical results for the adsorption of a particle and a v = 0.6 oblate vesicle. The numerical results, represented here by circles and squares, were obtained in the same way as in our previous paper.[17]

4. Summary

Starting from a general coordinate setup, we demonstrated that for an adhering small spherical particle the contact line that defines the wrapping edge of a membrane is a perfect circle on the sphere. This defines a local symmetric axis, although at a larger scale the vesicle could be in a non-axisymmetric shape. We showed how the total energy of the system consisting of a vesicle and an adhering small spherical particle can be obtained analytically from the properties of the mean curvature near the contact line. The result connects the energy with the originally unperturbed vesicle curvature, which can be calculated separately. For a vesicle made of lipid bilayer with no spontaneous curvature, we showed that the energetically preferred adhesion sites are those most concave positions on the original vesicle. We also generally determined the adhesion, engulfing, and budding boundaries for a vesicle, except for the adhesion-engulfing transition of a small particle to a prolate.

Our entire analysis was built on the basis of taking the leading order in the expansion of the shape equation on a small parameter RpK0, where Rp is the radius of the spherical particle and K0 is a typical membrane curvature. The analytic results were verified by a number of examples, where the numerical solution independent of the current approach is available.

The conformations of some states studied in this paper are similar to those found in biological processes, such as endocytosis and exicytosis. Given that biological systems are much more complicated, the successful application of the current work in these processes remains to be seen.

Reference
1 Hefrich W 1973 Z. Naturforsch. C 28 693 [Cited within:2]
2 Seifert U 1997 Adv. Phys. 46 13 DOI:10.1080/00018739700101488 [Cited within:3]
3 Muller M, Katsov K and Schick M 2006 Phys. Rep. 434 113 DOI:10.1016/j.physrep.2006.08.003 [Cited within:2]
4 Deuling H J and Helfrich W 1976 J. Phys. 37 1335 DOI:10.1051/jphys:0197600370110133500 [Cited within:1]
5 Seifert U, Berndl K and Lipowsky R 1991 Phys. Rev. A 44 1182 DOI:10.1103/PhysRevA.44.1182 [Cited within:5]
6 Pelkmans L, Kartenbeck J and Helenius A 2001 Nature Cell Biol. 3 473 DOI:10.1038/35074539 [Cited within:1]
7 Sieczkarski S B and Whittaker G R 2002 J. Gen. Viro. 83 1535 [Cited within:1]
8 Pietiainen V, Marjomaki V, Upla P, Pelkmans L, Helenius A and Hyypia T 2004 Mol. Biol. Cell 15 4911 DOI:10.1091/mbc.E04-01-0070 [Cited within:1]
9 Seifert U 1991 Phys. Rev. A 43 6803 DOI:10.1103/PhysRevA.43.6803 [Cited within:1]
10 Seifert U and Lipowsky R 1990 Phys. Rev. A 42 4768 DOI:10.1103/PhysRevA.42.4768 [Cited within:7]
11 Deserno M 2004 Phys. Rev. E 69 31903 DOI:10.1103/PhysRevE.69.031903 [Cited within:3]
12 Nowek S A and Chou T 2008 Phys. Rev. E 78 021908 DOI:10.1103/PhysRevE.78.021908 [Cited within:1]
13 Deserno M and Bickel T 2003 Europhys. Lett. 62 767 DOI:10.1209/epl/i2003-00438-4 [Cited within:1]
14 Deserno M 2004 J. Phys. : Condens. Matter 16 S2061 DOI:10.1088/0953-8984/16/22/004 [Cited within:3]
15 Noguchi H and Takasu M 2002 Biophys. J. 83 299 DOI:10.1016/S0006-3495(02)75170-9 [Cited within:2]
16 Deserno M and Gelbart W M 2002 J. Phys. Chem. B 106 5543 DOI:10.1021/jp0138476 [Cited within:5]
17 Cao S, Wei G H and Chen J Z Y 2011 Phys. Rev. E 84 050901 DOI:10.1103/PhysRevE.84.050901 [Cited within:10]
18 Niu Y Q, Wei W, Zheng B, Zhang C X and Meng Q T 2014 Acta Phys. Sin. 63 038701(in Chinese) DOI:10.7498/aps.63.0387012014 [Cited within:1]
19 Zheng B and Meng Q T 2014 Chin. Phys. B 23 038701 DOI:10.1088/1674-1056/23/3/038701 [Cited within:1]
20 Niu Y Q, Wei W, Zheng B, Zhang C X and Meng Q T 2013 Chin. Phys. B 22 128701 DOI:10.1088/1674-1056/22/12/128701 [Cited within:1]
21 Zhang J, Das S and Du Q 2009 J. Comp. Phys. 228 7837 DOI:10.1016/j.jcp.2009.07.027 [Cited within:2]
22 Zhao Y, Das S and Du Q 2010 Phys. Rev. E 81 041919 DOI:10.1103/PhysRevE.81.041919 [Cited within:2]
23 Ou-Yang Z C and Helfrich W 1987 Phys. Rev. Lett. 59 2486 DOI:10.1103/PhysRevLett.59.2486 [Cited within:2]
24 Ou-Yang Z C and Helfrich W 1989 Phys. Rev. A 39 5280 DOI:10.1103/PhysRevA.39.5280 [Cited within:1]
25 Capovilla R and Guven J 2002 J. Phys. A 35 6233 DOI:10.1088/0305-4470/35/30/302 [Cited within:1]
26 Guven J 2004 J. Phys. A 37 L313 DOI:10.1088/0305-4470/37/28/L02 [Cited within:2]
27 Benoit J and Saxena A 2007 Phys. Rev. E 76 041912 DOI:10.1103/PhysRevE.76.041912 [Cited within:1]
28 Góźdź W T 2007 Langmuir 23 5665 DOI:10.1021/la063522m [Cited within:1]
29 Zimmerberg J and Kozlov M M 2006 Nature Rev. Mol. 7 9 DOI:10.1038/nrm1784 [Cited within:1]
30 Weikl T R 2003 Eur. Phys. J. E 12 265 DOI:10.1140/epje/i2003-10058-x [Cited within:3]
31 Muller M M, Deserno M and Guven J 2005 Euro. Phys. J. 69 482 DOI:10.1209/epl/i2004-10368-1 [Cited within:1]
32 Muller M M, Deserno M and Guven J 2007 Phys. Rev. E 76 011921 DOI:10.1103/PhysRevE.76.011921 [Cited within:1]
33 Das S and Du Q 2008 Phys. Rev. E 77 011907 DOI:10.1103/PhysRevE.77.011907 [Cited within:1]
34 Chen J Z Y, Liu Y and Liang H J 2009 Phys. Rev. Lett. 102 168103 DOI:10.1103/PhysRevLett.102.168103 [Cited within:1]
35 Mkrtchyan S, Ing C and Chen J Z Y 2010 Phys. Rev. E 81 011904 DOI:10.1103/PhysRevE.81.011904 [Cited within:1]
36 Chen J Z Y and Mkrtchyan S 2010 Phys. Rev. E 81 041906 DOI:10.1103/PhysRevE.81.041906 [Cited within:3]
37 Chen J Z Y 2010 Phys. Rev. E 82 060801 DOI:10.1103/PhysRevE.82.060801 [Cited within:1]
38 Su Y C and Chen J Z Y 2013 Soft Matter 9 570 DOI:10.1039/C2SM26770E [Cited within:1]
39 Deserno M, Müller M M and Guven J 2007 Phys. Rev. E 76 011605 DOI:10.1103/PhysRevE.76.011605 [Cited within:3]
40 Rodriguez-Garcia L R Arriaga, Mell M, Moleiro L H and Lopez-Monteroand Monroy F 2009 Phys. Rev. Lett. 102 128101 DOI:10.1103/PhysRevLett.102.128101 [Cited within:1]