†Corresponding author. E-mail: lysenko_@ukr.net
We construct a cubically nonlinear theory of plural interactions between harmonics of the growing space charge wave (SCW) during the development of the two-stream instability. It is shown that the SCW with a wide frequency spectrum is formed when the frequency of the first SCW harmonic is much lower than the critical frequency of the two-stream instability. Such SCW has part of the spectrum in which higher harmonics have higher amplitudes. We analyze the dynamics of the plural harmonic interactions of the growing SCW and define the saturation harmonic levels. We find the mechanisms of forming the multiharmonic SCW for the waves with frequencies lower than the critical frequency and for the waves with frequencies that exceed the critical frequency.
Free-electron lasers (FEL) using two-stream relativistic electron beams attract attention of researchers primarily due to their exceptionally high amplification properties in the millimeter to infrared wavelength range.[1– 19] High growth increments of electromagnetic waves in such FEL are achieved through the use of the two-stream instability.[1, 20, 21] In most papers devoted to two-stream FEL, monochromatic operation modes are investigated. In such modes, the excited space charge wave at the fundamental frequency has a maximal gain due to the two-stream instability. In recent years, there are also works devoted to multi-harmonic operation modes of two-stream FEL.[1, 10, 22] In those works, cluster FELs, which are able to form clusters of a powerful ultrashort electromagnetic field, are investigated. The operation of such devices is based on the synthesis of an ultrashort cluster from many harmonics. The shape of the ultrashort cluster is similar to the Dirac delta function. It means that the spectrum of such clusters has to be similar to that of the Dirac delta function and has to consist of the plurality of harmonics with comparable amplitudes. This raises the problem of creating a wave source with a broad frequency spectrum.
As shown by the preliminary analysis, if the frequency of the first harmonic of the growing SCW in a two-stream electron beam is much smaller than the critical frequency of the two-stream instability, the multi-harmonic SCW, which consists of tens of harmonics with comparable amplitudes, is excited in such a system.[1, 10, 22, 23] The multi-harmonic SCW is excited due to the fact that such a wave is characterized by quasi-linear dispersion characteristics. Therefore, frequencies and wave numbers of such wave harmonics satisfy the three-wave parametric resonance conditions. As a result, the harmonics are amplified due to both the two-stream instability and the plurality of the three-wave parametric resonances. Thus, the overall dynamics of the wave harmonics in the two-stream electron beam is quite complex.
The presented paper is devoted to the analysis of the dynamics of the space-charge wave, which is characterized by a wide frequency spectrum, during the development of the two-stream instability. Problems associated with the excitation of the multiharmonic SCW were studied previously.[1, 10, 22, 23] However, in those papers, features of the dynamics of such waves have not been studied, and the mechanisms of harmonic excitations in different frequency ranges have not been found.
We consider the physical processes in a two-stream electron beam, which is characterized by almost the same partial relativistic velocities υ 1, υ 2 (υ 1 − υ 2 < < υ 1, υ 2) directed along the Z axis of the system and equal partial plasma frequencies ω p1 = ω p2 = ω p. The space charge of the beam is neutralized by an ion background and the beam is homogenous in the transverse plane.
The electric field of the SCW, which determines the dynamics of the two-stream instability, takes the multi-harmonic form

Here E is the electric field; Em is the electric field strength of the m-th harmonic; N is the number of harmonics that are taken into account in solving the problem; pm = ω m − kmz is the phase, ω m is the frequency, and km is the wavenumber of the m-th harmonic of SCW; and ez is the unit vector codirectional with the Z axis.
We consider the situation when the two-stream instability is excited in the relativistic two-stream electron system. For this purpose, the frequency of the SCW has to be lower than the critical frequency of the two-stream instability[1, 20, 21]

Here δ = (υ 1 − υ 2)/(υ 1 + υ 2), γ 0 = (γ 1 + γ 2)/2, 

In many studies of two-stream free electron lasers, the frequency of the first SCW harmonic coincides with the optimal frequency ω opt. In this paper, we consider a different situation, i.e., the frequency of the first SCW harmonic is much lower than the optimal frequency and hence lower than the critical frequency

As an appropriate analysis shows, in this case, the relation between wavenumbers and frequencies of the SCW turns out to be quasi-linear.[1, 20, 21] This leads to the fact that in the two-stream system, the three-wave parametric resonance conditions

or

are satisfied for a plurality of SCW harmonics whose frequencies are lower than the critical frequency (ω < ω cr). In Eq. (5), m1, m2, and m3 are the numbers of harmonics.
Formation of SCW with a wide multi-harmonic spectrum in which higher harmonics have higher amplitudes is the result of the plurality of the three-wave parametric resonance interactions. Let us consider the dynamics of such multiharmonic SCW.
First, we use the relativistic quasi-hydrodynamical equation (see, e.g., Ref. [1])

the continuity equation

and Maxwell’ s equations
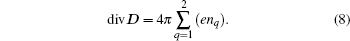
In these equations, υ q is the velocity vector of the q-th component of the beam (q = 1, 2); ν is the frequency of particle collisions; B is the magnetic induction; nq is the particle concentration of the q-th component of the beam; υ T is the root mean square velocity of particle thermal motion; r is the spatial coordinate of the observation point; and e = − | e| and me are the electron charge and the electron mass, respectively. In this paper, we assume that the collisions between particles and the thermal motion of electrons can be ignored, i.e., υ T = 0, ν = 0.
To solve the problem of motion and find the concentration of electrons in the beam, we use the method of averaging characteristics.[1, 22] This method uses the Krylov– Bogolyubov averaging method[1, 24] for the asymptotic integration of differential equations. The problem of electromagnetic field excitation is solved using the method of slowly varying amplitudes. We assume that the quasistationary mode of interaction is realized and the harmonic amplitudes depend only on the z coordinate and are independent of time t. We carry out mathematical transformations and obtain a set of differential equations for the electric field strength of the SCW harmonic in the cubic-nonlinear approximation

It must be noted that equation (9) consists of N equations (index m of the harmonic number is from 1 to N). Here,

is the dispersion function of the m-th harmonic of the SCW, C1, m = ∂ D(ω m, km)/∂ (− ikm), C2, m = ∂ 2D(ω m, km)/∂ (− ikm)2/2, and Fm = Fm(E1, E2, … , EN) are the non-linear functions, which describe the interaction of the SCW harmonics. The set of equations (9) allows us to investigate multi-harmonic processes in the two-stream system in the cubic-nonlinear approximation.
It is known that the two-stream instability is realized when the frequency of the space charge wave is lower than the critical frequency (ω < ω cr).[1, 20, 21] From a mathematical point of view, it means that under such conditions, the dispersion equation

has complex solutions (hereafter, if possible the subscript m is omitted and D(ω , k) is given by Eq. (10)). The analysis of the dispersion equation (11) shows that these complex solutions have the following form:

where υ 0 = (υ 1 + υ 2)/2, υ 1, 2 are the partial velocities of the partial electron beams; and iΓ is the imaginary non-linear term in the wavenumber of the SCW.[1, 20, 21] Thus, among the solutions of Eq. (11), there are two waves which are characterized by complex wavenumber k. One of these waves grows exponentially (this wave is referred to as growing), and Γ has the physical meaning of growth rate for this wave. The other wave damps exponentially (damped wave). As the amplitude of the damped wave decreases rapidly, we shall not take account of this wave. It should be mentioned that, besides the two complex solutions (12), equation (11) for ω < ω cr also has two real solutions, which correspond to the slow wave and the fast wave. We assume that the amplitudes of the slow and the fast SCW are small, so the influence of these waves on the two-stream instability development can be ignored.
For the growing wave, the relation between the real part of the wavenumber and the frequency is linear as obtained from Eq. (12)

This means that if the frequency of the m-th harmonic ω m = mω 1 is m times greater than the frequency of the first harmonic ω 1, then the real part of the wavenumber of this harmonic Re(km) will be m times greater than the real part of the wavenumber of the first harmonic Re(k1)

Thus, the phase of the m-th harmonic (it is determined by the real part of the wavenumber)

is m times greater than the phase of the first harmonic. Therefore, the conditions of parametric resonances between harmonics (5) can reduce to the following form:

where m1, m2, and m3 are integers. Condition (14) is realized with the participation of a great number of harmonics, e.g., 3 = 2 + 1, 3 = 5 − 2, 3 = 7 − 4, 6 = 3 + 3, and so on. Therefore, we are talking about this situation as about that sort in which the plural parametric resonances are realized.
Thus, in the two-stream electron beam, the plural parametric resonances between harmonics of SCW are implemented through the linearity of the relation (13) between frequencies and wavenumbers. Due to the plural parametric resonances, a large number of SCW harmonics are excited.
As mentioned before, the key feature of the investigated model is that the frequency of the first SCW harmonic ω 1 does not coincide with the optimal frequency of the two-stream instability ω opt and satisfies the condition ω 1 ≪ ω cr. So we choose ω 1 = ω cr/20 as the frequency of the first harmonic. We investigate the physical processes in the relativistic two-stream system, taking into account 50 harmonics. In the case under consideration, the Langmuir frequencies are the same ω p1 = ω p2 = ω p and equal to 1.5 × 1011s− 1, the relativistic factors of the beams are γ 1 = 4.8 and γ 2 = 4.2.
Let us consider the dependence of growth increment Γ on frequency ω (Fig. 1). This dependence is easy to obtain through solving Eq. (11) numerically or analytically.[1, 20, 21] It follows from Fig. 1 that growth increment Γ has a maximum value when the frequency ω equals to the optimal one ω opt. When the frequency exceeds the optimal frequency ω > ω cr, the two-stream instability does not occur and Γ = 0. Therefore, if the frequency of the first harmonic equals the optimal one ω opt, the second harmonic will exceed the critical frequency ω cr and in this case only one harmonic will be amplified due to the two-stream instability. If the frequency of the first harmonic is much lower the optimal frequency hence the critical one, all the harmonics that satisfy the condition ω < ω cr will be amplified due to the two-stream instability. We investigate such situation in this paper. As shown in Fig. 1, for harmonics with frequencies lower than the optimal frequency, the growth increments of the higher harmonics exceed the growth increments of the lower ones. This makes us hope that SCW with abnormal spectrum, in which the harmonic amplitude increases with the increase of the harmonic number (frequency), can be formed as a result of the two-stream instability.
The results of the numerical analysis, which are obtained on the basis of Eq. (9), confirm the above assumptions. Figure 2 shows the dynamics of the SCW spectrum. Figures 2(a)– 2(c) show the spectra at z = 50 cm, z = 90 cm, and z = 100 cm, respectively. At the entrance (z = 0), the amplitude of the first harmonic is 10 V/cm, and other SCW harmonics are absent. As we can see, at the initial stage of multi-harmonic spectrum forming (Fig. 2(a)), higher harmonics are excited due to the plural parametric resonances. The amplitudes of these harmonics are decreasing with the increase of the harmonic number m. After that (Fig. 2(b)), an SCW with abnormal spectrum is formed due to the two-stream instability, which is characterized by the abnormal growth increment (see Fig. 1). Thus, the SCW, in which the harmonic amplitude increases with the increase of the harmonic number, can be formed. In this case, the fifth harmonic is maximal; whereas in the case of Fig. 2(a), the first harmonic is maximal. Figure 2(c) shows the SCW with a wide spectrum. The frequency of the harmonic with the maximal amplitude is equal to the optimal frequency ω opt. It is quite logical, because the maximal growth increment of the two-stream instability corresponds to this frequency. We can also see in Fig. 2(c) that in the system under consideration, the harmonics whose frequencies are above the critical frequency ω cr are excited (in Fig. 1, these harmonics are not excited). The frequency of the harmonic with the minimal amplitude does not correspond to the critical frequency (20th harmonic), but corresponds to frequency ω min (28th harmonic). There are non-zero harmonics with frequencies exceeding ω min. Let us find out what processes determine the formation of the harmonics.
 | Fig. 2. Dependence of SCW harmonic amplitude Em on harmonic number m at (a) z = 50 cm, (b) z = 90 cm, and (c) z = 100 cm. At the entrance (z = 0), the amplitude of the first harmonic is 10 V/cm, other harmonics are absent. The frequency of the first harmonic is ω 1 = 3.2 · 1011 s− 1, ω min is the frequency corresponding to the first spectral minimum. Calculations were performed with the same parameters as those in Fig. 1. |
First of all, it should be noted that the investigated SCWs with frequencies lower and higher than the critical frequency have different dispersions. Moreover, these cases correspond to different modes of interaction. The Raman mode of interaction occurs at frequencies ω < ω cr. While the quazi-Compton mode of interaction occurs at frequencies ω cr < ω < ω min. Let us discuss this in more detail.
As is well known, [1, 20, 21] the dispersion relation (13) is not satisfied for frequencies above the critical frequency. Figure 3 shows the dependence of wavenumber k on SCW frequency ω in the area of the critical frequency ω cr. The change of the dispersion is demonstrated in the bifurcation of the dispersion curve at frequencies above the critical frequency ω cr (point O): two curves OB and OC originate from one curve after point O. Therefore, the dispersion relation (13), which is represented by curve OA, does not coincide with any of the curves of eigenwaves OB and OC. This means that harmonics with phases mp1 and frequencies ω > ω cr are not eigenwaves for the system under consideration. This statement is valid only for the model when the spectral line width can be taken as zero. In a real situation, the harmonic amplitudes are not constant at ω > ω cr, they grow and therefore it is necessary to take into account their finite spectral width Δ k. If the spectral distances between curves OB and OA (AB, see Fig. 3), curves OC and OA (AC, see Fig. 3) are smaller or comparable with the spectral width Δ k, then the individual spectral lines OA, OB, and OC do not make any sense. This condition is referred to as the quazi-Compton mode of interaction.[1] The waves that are characterized by curves OA, OB, OC are indistinguishable and can be considered as eigenwaves for the system under consideration. Thus, in the frequency range ω cr < ω < ω min, the quazi-Compton interaction mode is realized, whereby the behavior of the SCW harmonics in this range is similar to that of the SCW harmonics with frequency ω < ω cr.
 | Fig. 3. Dependence of wavenumber k on SCW frequency ω in the area of the critical frequency ω cr. Two curves OB and OC originate from one at frequencies exceeding the critical frequency ω cr (point O). The dashed curve OA corresponds to dispersion relation (13). The curve OA above the critical frequency does not coincide with any of the curves of eigenwaves (OB and OC). Calculations were performed with the same parameters as those in Fig. 1. |
Based on the above, let us estimate the frequency ω min. We assume that the dynamics of waves with frequencies ω cr < ω < ω min is determined by the plural parametric resonances between the harmonics which have frequencies ω < ω cr and the increment values presented in Fig. 1. By analyzing the dependence of the growth increment on the frequency (Fig. 1), we can estimate the average growth rate as Γ aver ∼ 0.2 cm− 1 and assume that the half width of spectral line of waves in the range of the quazi-Compton mode of interaction ω cr < ω < ω min is (Δ k/2) ∼ Γ aver ∼ 0.2 cm− 1. Then frequency ω min is determined as frequency ω A (Fig. 3), at which (kB − kA) ∼ (kA − kC) ∼ Δ k ∼ 2Γ aver ∼ 0.4 cm− 1 (ω A and kA, kB, kC are the frequency and wavenumbers of the waves depicted by the corresponding points in Fig. 3). Based on this criterion, it is easy to find the frequency ω min. For the system under consideration, it is equal to ∼ 8.95 · 1012 s− 1 and coincides with ω min in Fig. 2(c), which corresponds to the first spectral minimum.
At frequencies higher than the minimal frequency ω min, there are non-zero harmonics of SCW (Fig. 2(c)) too. The harmonics in this frequency range are not eigenwaves, they occur due to the parametric resonances (interference) of SCWs. As a result of the interactions of the space charge waves, the shape of this part of the spectrum resembles interference patterns and has the interferential nature. The intensities of these harmonics are much smaller than those included in the main part of the spectrum (ω < ω min), but nevertheless, the total contribution of these harmonics in certain cases can be considerable.
We have constructed a cubically non-linear theory of plural harmonic interactions of the growing SCW during the development of the two-stream instability. It was shown that the conditions of three-wave parametric resonance are satisfied for all harmonics of the SCW whose frequencies are lower than the critical frequency of the two-stream instability due to the linearity of their dispersion characteristics. There is a simultaneous excitation of many harmonics as a result of the three-wave parametric resonances. These harmonics are growing as a result of parametric and two-stream instability. Then modes of interaction in which the excitation of plurality of higher harmonics with comparable amplitudes takes place become possible. We have analyzed the dynamics of the amplitudes of the interacting SCW harmonics and defined the saturation levels. We have found the mechanisms of forming the multi-harmonic SCW for the waves with frequencies lower than the critical frequency and for the waves with frequencies that exceed the critical frequency. For frequencies lower than the critical frequency, the formation of the SCW spectrum is caused by the two-stream instability, for frequencies in the range ω cr < ω < ω min, the quazi-Compton mode of interaction occurs, and when ω > ω min, the spectrum has the interference nature. It was proposed to use plural harmonic interactions of space-charge waves during the development of two-stream instability for generating SCWs with a wide frequency spectrum for cluster FELs.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|



