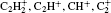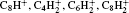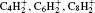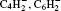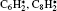Cite this Article
Liu Xiang-Mei†, Li Qi-Nan, Li Rui. Modeling of the nanoparticle coagulation in pulsed radio-frequency capacitively coupled C2H2 discharges . Chinese Physics B, 24(7): 075204  
Permissions
Modeling of the nanoparticle coagulation in pulsed radio-frequency capacitively coupled C2H2 discharges
Liu Xiang-Mei†, Li Qi-Nan, Li Rui
School of Science, Qiqihar University, Qiqihar 161006, China

†Corresponding author. E-mail: lxmjsc98@163.com

*Project supported by the Natural Science Foundation of Heilongjiang Province, China (Grant Nos. A2015011 and A2015010), the Postdoctoral Scientific Research Developmental Fund of Heilongjiang Province, China (Grant No. LBH-Q14159), the National Natural Science Foundation of China (Grant No. 11404180), and the Program for Young Teachers Scientific Research in Qiqihar University, China (Grant No. 2014k-Z11).

Abstract

The role of pulse parameters on nanoparticle property is investigated self-consistently based on a couple of fluid model and aerosol dynamics model in a capacitively coupled parallel-plate acetylene (C2H2) discharge. In this model, the mass continuity equation, momentum balance equation, and energy balance equation for neutral gas are taken into account. Thus, the thermophoretic force arises when a gas temperature gradient exists. The typical results of this model are positive and negative ion densities, electron impact collisions rates, nanoparticle density, and charge distributions. The simulation is performed for duty ratio 0.4/0.7/1.0, as well as pulse modulation frequency from 40 kHz to 2.7 MHz for pure C2H2 discharges at a pressure of 500 mTorr. We find that the pulse parameters, especially the duty ratio, have a great affect on the dissociative attachment coefficient and the negative density. More importantly, by decreasing the duty ratio, nanoparticles start to diffuse to the wall. Under the action of gas flow, nanoparticle density peak is created in front of the pulse electrode, where the gas temperature is smaller.

PACS: 52.65.–y; 52.27.Lw; 52.80.Pi
Keyword: nanoparticle coagulation; pulsed radio-frequency capacitively coupled acetylene discharges
1. Introduction

Formation of nanoparticles in reactive plasmas (C2H2, SiH4) is a phenomenon relevant in different areas of science and technology, such as fusion plasmas, [1] thin film deposition, [2, 3] microelectronic devices, [4] or extraterrestrial environments.[5] Among those applications, the presence of nanoparticles is deemed as a potential hazard, since they provide a significant source of film defects, and this problem is especially acute in the microelectronic industry. However, in certain material science applications, the amorphous carbon thin films composed of nanoparticles have efficient electron emission, making them a promising material for the field electron emitter fabrication.[6, 7] Therefore, a comprehensive understanding of the particle formation and growth mechanisms, charging and transport dynamics is indispensable. Based on experimental measurements[8, 9] and computer simulations, [10– 13] the basic reaction mechanisms of small species and the formation and growth mechanisms for negative ions are analyzed and discussed in a typical RF acetylene plasma. However, the simulation results for negative ions do not agree well with the experiment, which forces us to observe some new mechanisms for the formation and growth of negative ions. In 2008, Mao et al.[14] analyzed the initial step of nanoparticle formation and provided some possible routes for the larger hydrocarbons C2nH2 formation, which cause a considerable precursor for fast formation of negative ions. Currently, Ravi et al.[15] investigated the coagulation phase of nanoparticles, and showed that coagulation is significant for the first several seconds, while ceases when the particles are grown to several tens of nm in diameter. On this basis, Agarwal et al.[16] discussed the effects of size and charge distributions for larger negatively charged particles on coagulation.

Formation of nanoparticles results from a complex chemistry, which strongly depends on the plasma parameters: electron density, electron temperature, ion density, and gas temperature. In this article, the electron temperature is much lower during the off time, which is an important aspect of using the pulsed discharges. Under the faction of electron temperature, the pulse modulation of RF discharges can have higher average charged particle densities at the same average power and significantly lower wafer damage. Thus, the use of pulsed plasmas is considered as an effective way to control the growth process of particles.[17, 18] Moreover, pulsing the RF signal can prevent the dielectric from reaching a too high temperature for surface treatment. Based on experiment analysis, Berndt et al.[19, 20] presented a close correlation between the electron density and the charging and decharging of particles in a pulsed dusty plasma, which will influence the confinement of particles and then the spatial distribution of particles in the reactor. The goal of our work is to study the influence of the pulse parameters (for instance, the modulation frequency and duty cycle) on the nanoparticle formation and growth mechanisms, because by varying the pulse width and the pulse period, the plasma discharge mode can be modified. In C2H2 pulsed plasmas, the negative ions may be able to escape during the off time, which can be useful in processing.

Previous work[21] has shown that gas flow has a great effect on the nanoparticle density spatial distribution. Hence, in Section 2, the neutral gas equations including the density, flux, and energy balances are taken into account and the mechanisms for particle formation are also elaborated. In Section  3, simulation results for nanoparticle growth process are presented and the effects of the pulse parameters on the particle formation mechanisms and plasma dynamics are studied. We conclude in Section  4.

2. Theoretical model
2.1. Plasma kinetics

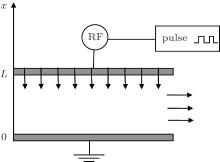
The schematic diagram of the pulsed radio-frequency capacitively coupled plasma reactor is shown in Fig.  1, where the lower electrode is grounded and the pulse showerhead electrode is placed 3.0  cm higher. The pulse showerhead electrode is taken as a uniformly porous wall with a homogeneous gas flow into the reactor crossing its whole area. The gas pumping is across the sidewall.

Fig.  1. Schematic diagram of the pulsed radio-frequency capacitively coupled plasma reactor.

The fluid model we used in the present study has been described in detail previously.[22, 23] The major goal of this model is to investigate effects of the pulse parameters (duty cycle, modulation frequency, discharge power) on the formation and growth mechanisms of dust particles. Fifty-seven different species including electrons, ions, neutrals, and radicals are taken into account, which are given in Table  1. The following is the main content of the fluid model. For electrons, the continuity, momentum, and energy equations are taken into account. However, at a pressure not too low, the momentum equation can be estimated by drift– diffusion approximation since the momentum transfer frequency for electrons is about 3000  MHz, much larger than the pulsed radio-frequency source. That is to say, electrons can react instantaneously to a change of the electric field.

Table 1. Overview of different species incorporated in this model.

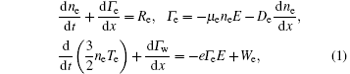
where ne, Te, Γ e, and Γ w are the density, temperature, flux, and energy density flux for electrons, De is the electron diffusion coefficient, and μ e is mobility. The Re represents the electron source and sink terms, while We expresses the electron energy loss. An important approximation is that we calculate the electron energy distribution function (EEDF) from the Boltzmann equation in a two-term approximation, since the plasma-neutral collision frequency is a little larger than the plasma frequency sometimes, and then the EEDF deviates from a Maxwellian distribution.[14]

For ions, the continuity and momentum equations are used to study the ion density ni and ion flux Γ i. Under low pressures, the ion directed energy is much larger than the ion thermal energy, [14] thus the calculation results are not strongly affected by the ion temperature Ti, and then the ion temperature is assumed to be 400  K. In this case, the ion momentum equation is estimated by drift– diffusion approximation

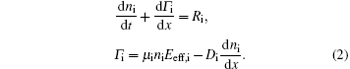
Here μ i and Di are ions’ mobility and diffusion coefficient, and Ri represents the ion source and sink terms. Note that the characteristic momentum transfer frequency for ions is only a few  MHz, thus the ion inertia effects arising from lower momentum transfer frequency are dominant under the low-pressure conditions. Then an effective electric field Eeff, i given by dEeff, i/dt = (e/μ imi)(E − Eeff, i) is introduced in Eq.  (2).

The electric field E is determined by the Poisson equation

where ε 0 is the free space permittivity, Zd = Qd/e is the number of elementary charges, e represents the elementary charge, and the nanoparticle charge Qd is given by

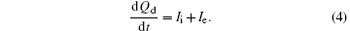
Here the electron current Ie and the ion current Ii are given by the orbital motion limited theory (OML)[24]

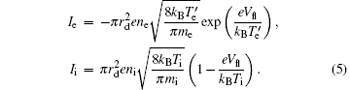
The Poisson equation is coupled to the particle’ s balance equations, making the model fully self-consistent.

For neutral species, a neutral reacting flow is described by the mass continuity equation solved for interchangeably mass density nn, the energy balance equation for neutral gas temperature Tn, and the momentum balance equation for axial mass-averaged velocity un

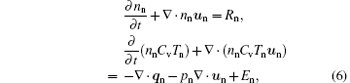
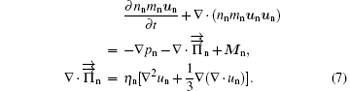
Here, Rn expresses the neutral gas production and loss terms, Cv is the heat capacity at constant volume, qn is the neutral heat flux vector, and En represents the energy transfer owing to the neutral species colliding with other species. Mn is the momentum transfer of neutral gas colliding with other species, mn and pn are the neutral gas mass and pressure. Assuming that the fluid is incompressible and viscosity is constant across the fluid, thus a Newtonian form for the neutral viscous stress tensor is introduced in Eq.  (7). The η n is the viscosity coefficient, which plays the role of a diffusion coefficient. While the viscosity term arising from the non-diagonal components of the pressure tensor can be considered as the momentum diffusion.

2.2. Nanoparticle formation

For nanoparticles, a continuum equation is introduced to describe the spatial and temporal variation of particle, in which the source term Rd consists of four parts: nucleation term, growth term, surface deposition term, and charge fluctuations term. Taking into account nanoparticles immersed in a plasma affected by different forces, including electrostatic force, neutral drag, ion drag, gravity, and thermophoresis. Assuming that the neutral drag balances all the other forces, the nanoparticle’ s flux Γ d can be obtained and expressed as a drift diffusion equation[7]

Here, nd, rd, μ d, and Dd are the density, radius, mobility, and diffusion coefficient for nanoparticles, g expresses the gravitational acceleration, kT is the thermal conductivity, υ s is the ion mean speed, υ th the average thermal velocity, mi and md are the ion mass and nanoparticle mass, respectively,

is the momentum loss frequency, and Γ is the Coulomb logarithm.

Following gas phase nucleation by growth of negative ions, a phase of rapid growth by coagulation of clusters sets in, which results in larger-size particulars at densities much below that of the clusters.[24] To obtain more information about coagulation, aerosol physics is used and considered as a good technique. More importantly, an excellent assumption for the conditions of interest is made. In this code, the general dynamic equation is usually used to describe the nanoparticle density, and the coagulation coefficient β 1, 2 between two coagulating particles with volumes v1 and v2 in the free molecular regime (the dust particle Knudsen number Kn ≫ 1) can be described by

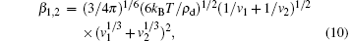
where kB and T are the Boltzmann constant and the absolute temperature, ρ d is the mass density of material. Note that in this model, dust particle is deemed to be unity sticking coefficients, and the effect of van der Waals forces is not taken into account. In our calculation, 40 sections are divided logarithmically in the volume domain, while the smallest volume section is 0.2  nm3, corresponding to the size of C12H− , and the largest volume section is 50.0  nm in diameter.

3. Results and discussion

In this section, the calculation results for the pulsed radio-frequency acetylene discharges are presented. The plasma process parameters are as follows: electrode spacing is 3.0  cm, ion temperature is 400  K, gas flow rate is 40  sccm, gas pressure is 500  mTorr, and pulse frequency is 13.56  MHz. All the calculations are performed in pulsed discharges at a duty ratio of 0.4/0.7/1.0, and the modulation frequency varies from 40  kHz to 2.7  MHz.

Since the secondary electron is not taken into account, the pulsed discharge results are limited to the α regime. The simulation grid consists of 125 cells in the axis direction, while the time step Δ t = 7.4 × 10− 12  s (10000 time steps per RF period). A much longer time step of 7.4 × 10− 9  s is applied for the description of the neutral– neutral chemistry to speed up the calculations. The nanoparticle transport in the coagulation module is also investigated by using the same temporal resolution. The calculation results given below are based on the system in a steady state, typically after the relative variations of the plasma parameters between two succeeding pulse cycles are less than 10− 4.

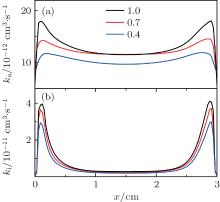
To assess the pulse parameter effect on the electron impact collisions. Figure  2 illustrates the dissociative attachment coefficient (ka) and the dissociative ionization coefficient (ki) profiles for acetylene at different duty ratios: 0.4, 0.7, 1.0, and the corresponding pulse length is 25  μ s. It must be noted here that the values of ki and ka increase with the duty ratio. This is due to the fact that a much higher energy is produced by applying continuous voltage. We can also found from Fig.  3 that for the continuous wave case, the dissociative attachment coefficient and the dissociative ionization coefficient first increase sharply to peak values at the presheaths for the electric field effect. Afterward, ki and ka fall in the bulk plasma and approach quasi-steady values. However, the maximum values at the presheaths drop rapidly with decreasing duty ratio, especially for the dissociative attachment coefficient in Fig.  2(a). This can be explained by the fact that higher collision energy losses when the pulse is turned off. Thus, more electron– ion pairs are able to flow to the walls by diffusive, and then the gradient of the dissociative attachment coefficient becomes very small. Compared with the value of dissociative attachment coefficient with the dissociative ionization coefficient, we can find that the dissociative ionization coefficient increases at a considerably slower rate than the dissociative attachment coefficient at the presheaths, as shown in Fig.  2(b).

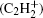
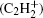
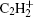
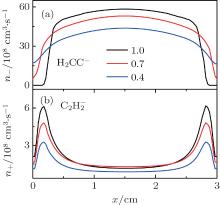Figure  3 presents the variation of density profiles for the negative ion (H2CC− ) and positive ion at different duty ratio. Based on the experiment of Deschenaux et al., [8] 95% of the production from dissociative electron attachment on C2H2 is assumed to be H2CC− . Therefore, H2CC− is a main precursor for the dust formation. It is clear from Fig.  3 that a gradually increasing trend of H2CC− and density can be observed as the duty ratio increases, under the influence of the dissociative attachment coefficients and dissociative ionization coefficients. However, H2CC− is confined in the plasma for the continuous case, but starts to diffuse to the wall when operating a pulsed discharge, due to the fact that less electron density can be obtained when the pulse is turned off, and then the space charge potential no longer confines the negative ions. Thus, there is a significant negative ion flux to the walls. Influenced by the dissociative ionization coefficient (Fig.  2), exhibits two prominent peaks at the presheaths, and almost constant in the plasma bulk, as shown in Fig.  3(b).

Fig.  2. Spatio variation profiles of the dissociative attachment coefficients (ka) (a) and the dissociative ionization coefficients (ki) (b) for different duty ratio within one pulse period: η = 0.4, 0.7, and 1.0.

Fig.  3. Spatio-temporal variation profiles of the negative ion (H2CC− ) (a) and positive ion (b) within one pulse period, with the same settings as those in Fig.  2.

The nanoparticle density (nd) and charge (Qd) profiles with a diameter of 5  nm are shown in Fig.  4. As we know form Eqs.  (8) and (9), negative ion density (as shown in Fig.  3) and ion flux are the main parameters that nanoparticle density nd depends on. Thus, nd increases rapidly with increasing duty ratio from 0.4 to 1.0. Moreover, since the gas flow is taken into account, a gas temperature gradient is presented in the discharge, which will make the gas molecules transfer more momentum from the hotter area of the plasma to the cooler area, and then a local maximum is created in front of the upper electrode.[21] However, in this work, we observe that by varying duty ratio, the peak of nanoparticle density gradually flow to the upper electrode. This is due to the fact that the negative ion density (H2CC− ) can diffuse to the wall in the pulse-off time, which is the main initial particle for the nanoparticle formation. These results imply that the duty ratio can easily be used to drive nanoparticles to the upper electrode, and thus pulsed power modulation can be one obvious way to minimize substrate contamination. Compared with the nanoparticle density, nanoparticle charge Qd just increase with increasing duty ratio, especially in the sheath regions as shown in Fig.  4(b), since Qd mainly depends on the electron and positive ion densities. We can also see that the charge Qd exhibits a prominent peak near the presheath for the electric field effect and decreases rapidly in the sheath region with less electrons collision.

Fig.  4. Spatial variation profiles of the nanoparticle number density nd (a) and nanoparticle charge Qd (b) within one pulse period, with the same settings as those in Fig.  2.

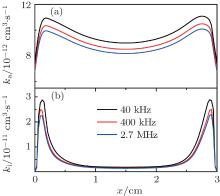
The role of pulse modulation frequency on the electron impact collisions rate is also discussed. Figure  5 presents the dissociative attachment coefficient (ka) and the dissociative ionization coefficient (ki) profiles at different modulation frequencies: 2.7  MHz, 400  kHz, 40  kHz, while the duty ratio is fixed at 0.4. It was found that ka and ki increase with decreasing processing modulation frequency. This is due to the fact that as the modulation frequency decreases, a relatively longer pulse-on time is applied, resulting in larger electron energy and larger collisions rate. Thus, as the modulation frequency varies from 2.7  MHz to 40  kHz, the dissociative attachment coefficient and the dissociative ionization coefficient increased by a factor of 1.1 and 1.3, respectively. We also observe that when the modulation frequency is lower than 100  kHz, the coefficients ka and ki vary very little with the modulation frequency.

Fig.  5. Spatial variation profiles of the dissociative attachment coefficients (ka) (a) and the dissociative ionization coefficients (ki) (b) for different pulse modulation frequencies within one pulse period: fm = 40  kHz, 400  kHz, 2.7  MHz.

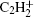
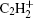
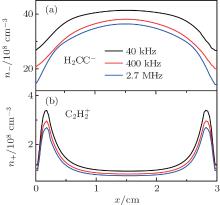The ion densities of H2CC− and as a function of modulation frequency are plotted in Fig.  6. Calculations have been performed for three different modulation frequencies ranging between 2.7  MHz and 40  kHz, with the duty ratio of 40%. As we know, decreasing the pulse modulation frequency tends to increase the pulse-on time, and then plasma density will increase. Thus, we observe that H2CC− density increases by 12%, while density increases 20% with decreasing modulation frequency in this simulation. Furthermore, as the modulation frequency decreases, more negative ions will diffuse to the wall. It is attributed to the fact that, at the modulation frequency of 40  kHz, there is a relatively longer pulse-off time, which will make the electron density drop to a much lower value compared to H2CC− . This finally leads to a larger diffusive flux of negative ions to the wall.

Fig.  6. Spatial variation profiles of the negative ion (H2CC− ) (a) and positive ion (b) within one pulse period, with the same settings as those in Fig.  5.

The nanoparticle density and charge profiles of several modulation frequencies are shown in Fig.  7 at a size of 5  nm. We can see from Fig.  7(a) that as the modulation frequency decreases, nanoparticle density is increased slightly, and gradually diffuses to the upper electrode. This is due to the fact that the smaller modulation frequency, the longer pulse-off time, and more negative ion (such as H2CC− ) will diffuse to the wall. Meanwhile, H2CC− is the main initial particle for nanoparticle formation, [21] thus nanoparticles gradually flow towards the upper electrode with the decrease of modulation frequency. This implies that by decreasing the modulation frequency, nanoparticles can be able to flow the wall, and the plasma density is effectively increased. The nanoparticle charge in Fig.  7(b) is strongly affected by the positive ion density (as shown in Fig.  6(b)). Thus, the nanoparticle charge increases with decreasing pulse modulation frequency.

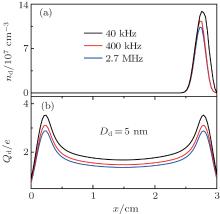Fig.  7. Spatial variation profiles of the nanoparticle number density nd (a) and nanoparticle charge Qd (b) within one pulse period, with the same settings as those in Fig.  5.

4. Concluding remarks

By using a self-consistent one-dimensional fluid model and an aerosol dynamics model, we have presented the fast coagulation stage in pulsed capacitively coupled acetylene discharges, in which nanoparticles can grow from smaller vinylidene anion. This model contains neutral reacting flows, and hence the gas temperature is not a constant and the thermophoresis force is taken into account. In this work, the variations of plasma density distribution, electron impact collisions coefficient distribution, nanoparticle density distribution, and charge distribution were calculated in the plasma reactor for various process conditions (duty ratio, pulse modulation frequency).

Similar to what we have learned in pulsed electronegative discharges, the duty ratio has a great effect on the negative ion density, owing to the dissociative attachment coefficient affect. We note in our work that as the duty ratio decreases, the maximum values of dissociative attachment coefficient at the presheaths drop rapidly, while the negative ion density starts to diffuse to the wall. On this basis, we observed that decreasing the duty ratio can not only increase the value of nanoparticle density, but also make the nanoparticles flow towards the pulse powered electrode. However, the pulse modulation frequency has a relatively smaller impact on the nanoparticle density. These results imply that by properly pulsing the discharge, the nanoparticle density in the sheath region can be significantly reduced, without reducing significantly the plasma density.

Reference
1 Winter J 2004 Plasma Phys. Control. Fusion 46 B583 DOI:10.1088/0741-3335/46/12B/047 [Cited within:1]
2 Hong S, Berndt J and Winter J 2003 Plasma Sources Sci. Technol. 12 46 DOI:10.1088/0963-0252/12/1/306 [Cited within:1]
3 Kersten H, Deutsch H, Stoffels E, Stoffels W W, Kroesen G M W and Hippler R 2001 Contrib. Plasma Phys. 41 598 DOI:10.1002/(ISSN)1521-3986 [Cited within:1]
4 Selwyn G S, Singh J and Bennet R S 1989 J. Vac. Sci. Technol. A 7 2758 DOI:10.1116/1.576175 [Cited within:1]
5 Kovačević E, Stefanović I, Berndt J, Pendleton Y J and Winter J 2005 Astrophys. J. 623 242 DOI:10.1086/apj.2005.623.issue-1 [Cited within:1]
6 Ostrikov K 2005 Rev. Mod. Phys. 77 489 DOI:10.1103/RevModPhys.77.489 [Cited within:1]
7 Xu N S and Huq S E 2005 Mater. Sci. Eng. R. 48 47 DOI:10.1016/j.mser.2004.12.001 [Cited within:2]
8 Deschenaux Ch, Affolter A, Magni D, Hollenstein Ch and Fayet P 1999 J. Phys. D: Appl. Phys. 32 1876 DOI:10.1088/0022-3727/32/15/316 [Cited within:2]
9 Benedikt J, Consoli A, Schulze M and von Keudell A 2007 J. Phys. Chem. A 111 10453 [Cited within:1]
10 Doyle J R 1997 J. Appl. Phys. 82 4763 DOI:10.1063/1.366333 [Cited within:1]
11 Herrebout D, Bogaerts A, Gijbels R, Goedheer W J and Vanhulsel A 2003 IEEE Trans. Plasma Sci. 31 659 DOI:10.1109/TPS.2003.815249 [Cited within:1]
12 Stoykov S, Eggs C and Kortshagen U 2001 J. Phys. D: Appl. Phys. 34 2160 DOI:10.1088/0022-3727/34/14/312 [Cited within:1]
13 De Bleecker K, Bogaerts A and Goedheer W 2006 Phys. Rev. E 73 026405 DOI:10.1103/PhysRevE.73.026405 [Cited within:1]
14 Mao M, Benedikt J, Consoli A and Bogaerts A 2008 J. Phys. D: Appl. Phys. 41 225201 DOI:10.1088/0022-3727/41/22/225201 [Cited within:3]
15 Ravi L and Girshick S L 2009 Phys. Rev. E 79 026408 DOI:10.1103/PhysRevE.79.026408 [Cited within:1]
16 Agarwal P and Girshick S L 2012 Plasma Sources Sci. Technol. 21 055023 DOI:10.1088/0963-0252/21/5/055023 [Cited within:1]
17 Bouchoule A, Plain A, Boufendi L, Blondeau J Ph and Laure C 1991 J. Appl. Phys. 70 1991 DOI:10.1063/1.349484 [Cited within:1]
18 Heintze M and Magureanu M 2002 J. Appl. Phys. 92 2276 DOI:10.1063/1.1497457 [Cited within:1]
19 Berndt J, Kovačević E, Stefanović I and Boufendi L 2009 J. Appl. Phys. 106 063309 DOI:10.1063/1.3224874 [Cited within:1]
20 Berndt J, Kovačević E, Selenin V, Stefanović I and Winter J 2006 Plasma Sources Sci. Technol. 15 18 DOI:10.1088/0963-0252/15/1/003 [Cited within:1]
21 Liu X M, Li Q N and Xu X 2014 Chin. Phys. B 23 085202 DOI:10.1088/1674-1056/23/8/085202 [Cited within:3]
22 De Bleecker K, Bogaerts A, Gijbels R and Goedheer W 2004 Phys. Rev. E 69 056409 DOI:10.1103/PhysRevE.69.056409 [Cited within:1]
23 Khan S A and Hassan S 2014 J. Appl. Phys. 115 204304 DOI:10.1063/1.4878936 [Cited within:1]
24 Lieberman M A and Lichtenberg A J 2005 Principles of Plasma Discharges and Materials Processing2nd edn. New York Wiley-Interscience [Cited within:2]