Rescaled range analysis (R/S) is a statistical measure of the variability of a time series introduced by Hurst.^[1] The purpose of R/S is to provide an assessment of how the apparent variability of a series changes with the length of the time-period being considered. For a time series {x_i, i = 1, 2, … , N}, R/S is calculated as follows:

(i) Consider an m-dimensional sample series {y_i, i = 1, 2, … , m}, where m = sN, and s∈ (0, 1);

(ii) Then, compute the mean of the subseries {y_i},

(iii) Calculate the cumulative deviation Z(k) of the series {y_i},

(iv) Determine the range R_m = max{Z(k)) – min{Z(k)}, and the rescaled range (R/S)_m = R_m/S_m, where the S_m is the standard deviation for the subseries {y_i}, i = 1, 2, … , m}, and is expressed as

(v) Shift the subseries {y_i} with a step size of m without changing the length of the subseries, namely, {y_i, i = 1+ m, 2+ m, … , 2m}, and repeat steps (ii) to (iv);

(vi) Estimate the average rescaled range for each subseries;

(vii) Change the size m, and repeat the operation from steps (i) to (vi);

(viii) Create a double logarithm plot of the average of (R/S)_s versus m.

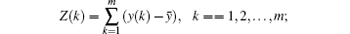
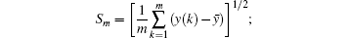
These steps can be summarized in the following equation:

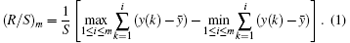
Hurst found that the ratio R/S is very well described for a large number of natural phenomena by the following empirical relation:

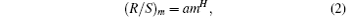
where a is a constant and H is the Hurst exponent. If the time series {x_i, i = 1, 2, … , N} is generated by a random walk, H has a value of 0.5, i.e., H = 0.5. If the Hurst exponent is less than 0.5 and greater than 0, the time series is uncorrelated. If the Hurst exponent is greater than 0.5, the time series is characterized by long-range correlation. If the Hurst exponent is 1.0, the time series exhibits the behavior of 1/f noise.

In the V/S algorithm, the rescaled variance statistic is described by the following equation^[19]

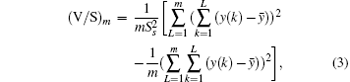
where V/S refers to variance, S_m.

The detailed descriptions of the MC-R/S and MC-V/S algorithms are as follows.

Step 1 Choose a window size M;

Step 2 Continuously cut sections of data with a length of M from the i-th data to the i + M-1th, i = 1, 1 + M, … , 1+ (n − 1)M, n = [N/M], where the symbol [ ] denotes the fetching integer andN is the total number of data. For example, [1000/30] = 33. Then, stitch the remaining parts together to obtain a new time series.

Step 3 Calculate the values of Hurst exponent H_i of the new time series (including N-M data) using R/S and V/S, respectively;

Step 4 Slide the window with a fixed size M in the original series, and repeat Steps 2 and 3 until reaching the end of the original series;

Step 5 Obtain a Hurst exponent series {H_i, i = 1, 2, … , n};

Step 6 Calculate the variance contributions of the Hurst exponent series in Step 5, and obtain the time-instant of any abrupt dynamic changes.

The logistic map is a polynomial map and is often cited as an archetypal example of how complex, chaotic behavior can arise from very simple nonlinear dynamic equations. Mathematically, the logistic map is written as follows:^[21]

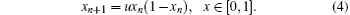
Here, x_n is a number between zero and one and it represents the ratio of existing population to the maximum possible population in year n. Thus, x₀ represents the initial ratio of the population in year 0. The u is a positive number and represents a combined rate of reproduction and starvation. The relative simplicity of the logistic map makes it an excellent point of entry to the concept of chaos. A rough description of chaos is that a chaotic system exhibits tremendous sensitivity to the initial conditions, with most values of u falling in a range between approximately 3.57 and 4 on the logistic map. In this study, x₀ = 0.8, and u = 3.8.

Figure  2 presents the MC-R/S and MC-V/S results for the artificial time series shown in Fig.  1(c). The abrupt change occurring from n = 301 to n = 330 can be identified equally using either MC-R/S or MC-V/S (Figs.  2(a) and 2(b)). The results shown in Figs.  2(a) and 2(b) indicate an abrupt decrease in the Hurst exponent series but fail to quantitatively indicate the specific time at which the abrupt change occurs. Thus, identification of the change point is left to the opinion of the analyst, based on a visual inspection of the Hurst exponent statistical graph.

In view of the sensitivity of the Hurst exponent to the data from different dynamic systems, He et al. presented a quantitative estimation method to identify the time-instants of abrupt changes based on the variance contribution of Hurst exponents.^[18] It should be noted that the average variance contribution procedure was calculated using all Hurst exponents, and the threshold of the variance contribution was set to be triple the average. The variance contribution can distinguish between normal and abnormal fluctuation amplitudes. Normal fluctuations are primarily caused by the small sample size, and abnormal fluctuations are primarily caused by the sensitivity of the calculation method for the Hurst exponent to the data from different dynamic systems.

Based on the definition of the threshold of variance contribution, it is easy to find that the variance contributions in the period from n = 301 to n = 330 are clearly greater than those in other parts in the artificial series for different window sizes, such as M = 2, 5, 10, and 15. It can therefore be concluded that an abrupt change in Hurst exponent occurs from n = 301 to n = 330 in the artificial series and that the detection results are robust for different window sizes. However, it must be noted that false detections for abrupt change points are more or less likely to be obtained for both MC-R/S or MC-V/S when the window size M is relatively small, such as M = 2 or 5 (Figs.  2(b) and 2(c)). It can be found that the positions of these false detections depend on the window size (Fig.  2). In particular, the positions of the false detections vary with window size, but the true positions of the abrupt change are hardly affected. The false detections can be clearly identified with larger window sizes.

Under identical computational conditions (Dell precision T3400), the computer times for running the MC-R/S and MC-V/S detection programs are presented in Table  1. In general, the computer time consumed by MC-V/S is approximately 25 times that of MC-R/S for an identical window size. Therefore, the operating efficiency of the MC-R/S algorithm is clearly much higher than that of the MC-V/S algorithm.

Noise is inevitable in observational data. In this subsection, the effects of noise on the performances of MC-R/S and MC-V/S are investigated. First, the performances of MC-R/S and MC-V/S are tested for detecting abrupt change in the artificial time series with a signal-to-noise ratio (SNR) of 30  dB. Similar to what has been done in Fig.  2, the abrupt change occurring from n = 301 to n = 330 can be identified equally well using either MC-R/S or MC-V/S (Figs.  2(a) and 2(b)) for different window sizes. When the window size is relatively small, e.g., M = 2 or M = 5, false detection results exist for both MC-R/S and MC-V/S. The false detection results disappear for MC-R/S after increasing the window size (Figs.  3(e) and 3(f)). Most of the false detection results also disappear for MC-V/S after increasing the window size, but very few false detection results remain, such as M = 10 and M = 15 (Figs.  3(e) and 3(f)). When the window size M is 30, both MC-R/S and MC-V/S can exactly detect the abrupt Hurst exponent change (the relevant figures are omitted here). When the values of SNR are 25  dB and 20  dB, showing that both noises are stronger than SNR = 30, similar results can be obtained and are therefore not discussed here in detail (see Appendices A and B)

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. MC-R/S and MC-V/S results for artificial time series and variance contributions of Hurst exponents. The results of (a) MC-R/S and (b) MC-V/S under different window scales, including M = 2, 5, 10, 15, and 30; variance contributions for detection results using MC-R/S (denoted by empty circles) and MC-V/S (denoted by solid circles), with window sizes M = 2 (c), 5 (d), 10 (e), and 15 (f). The dashed line represents the tripled average variance contribution of the Hurst exponent series.

Table 1.

Table 1.

Table 1. Computer running times of MC-R/S and MC-V/S for different window sizes (in units of s). Window size M = 2 M = 5 M = 10 M = 15 M = 30 MC-R/S 1.6703× 10− 3 6.656× 10− 4 3.313× 10− 4 2.156× 10− 4 1.047× 10− 4 MC-V/S 4.13922× 10− 2 1.611234× 10− 2 8.0485× 10− 3 5.275× 10− 3 2.5172× 10− 3

Table 1. Computer running times of MC-R/S and MC-V/S for different window sizes (in units of s).

When SNR is 15  dB, it can be observed from Figs.  4(a) and 4(b) that the Hurst exponents abruptly decrease when the data from n = 301 to n = 330 are removed. This abrupt decrease is mainly due to the different influences of the data from different dynamics on the calculation of Hurst exponents. The largest variance contribution is still roughly located between n = 301 and n = 330 for window sizes M = 2, 5, 10, 15, and 30 (Fig.  4). In addition, an abrupt increase in the Hurst exponent can be observed when the window size is relatively large, such as M = 10, 15, and M = 30. Comparing these results with the detection results shown in Figs.  2(a) and 2(b), it is easy to conclude that the noise in the artificial series with SNR of 15  dB causes the abrupt increases in Hurst exponent in some time periods. Variation analyses of the MC-R/S and MC-V/S results indicate that some false detections still exist when the window size is increased, unlike in the samples without noise. Particularly for some large window sizes, the variance contribution of false detection could approximate that of the actual abrupt change period as observed in Fig.  4(g). These results demonstrate that the strong noise can result in false detections for both MC-R/S and MC-V/S.

Fig.  3.

	Figure Option ViewDownloadNew Window
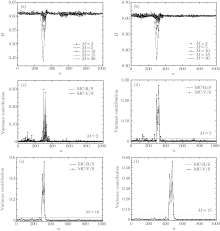	Fig.  3. The same as Fig.  2, but for the artificial time series with SNR = 30  dB.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Panels (a)– (f) being the same as Fig.  2, and panel (g) the same as Fig.  2(c) but for M = 30 and the artificial time series with SNR, = , 15  dB.

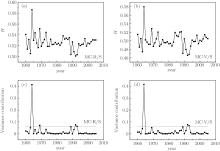
In addition to the above comparisons where an artificial time series is used, it is important to compare the performances of the MC-R/S and MC-V/S methods in detecting abrupt change in observational data. Here, the daily surface air pressure records are selected to further test the performances of the two methods. The records are from the Huma meteorological station in the Heilongjiang province, China. The detection results are shown in Fig.  5. It can be observed that the evolutionary trends of the Hurst exponents shown in Fig.  5(a) are similar to those in Fig.  5(b). They all reach a maximum value in 1964, which has significantly higher Hurst exponents compared with in the other years. To detect the exact moment of abrupt dynamic change in the air pressure records, the variance contributions of the Hurst exponents are analyzed. The evolutionary curves of the variance contributions in Figs.  5(c) and 5(d) are similar. The maximum values of the variance contributions are 41.2% and 41.4% , respectively, which are both far greater than the variance threshold (approximately 6.52% ). Moreover, the variance contributions in 1992 and 1993 are slightly greater than the thresholds in both the MC-R/S and MC-V/S results. To ensure the accuracy of the detection results, we use the MC-detrended fluctuation analysis (MC-DFA)^{[22, 23]} to detect the abrupt change in the records and find that cutting data from any year other than 1964 has very little effect on the Hurst exponents (the relevant figures are omitted here). Observational daily surface air pressure records from nearby stations have also been tested using MC-R/S, MC-V/S and MC-DFA, and the detection results similarly indicate that there is an abrupt dynamic change in 1964 in Huma.

Fig.  5.

Figure Option ViewDownloadNew Window

Fig.  5. The MC-R/S and MC-V/S results of Hurst exponents for daily surface air pressure records for the period from January 1, 1960 to December 31, 2006 at the Huma meteorological station in China, and the variance contribution analysis of the Hurst exponents with a one-year subseries length. Panel (a) shows the MC-R/S results, panel (b) the MC-V/S results, panel (c) the variance contribution analysis of the MC-R/S results, and panel (d) is the same as panel (c) but for the MC-V/S results. The dashed line represents the tripled average variance contribution of the Hurst exponent series.