In the last decades, the study of ultracold atoms in the optical lattices has attracted a lot of attention. Many interesting phenomena were observed in cold atomic systems, including the transition from the normal state to band insulators, ^[1] the Fermi superfluid, ^[2] the BEC– BCS crossover, ^[3] and the Cooper pairing in Fermi systems.^[4] Because of the high degree of control and the flexibility of the adjustable microscopic parameters in cold atomic systems, ranging from the dimensionality, interaction strength, and trapping potentials, experiments are set up to simulate the solid state models and even completely new systems that do not exist in the condensed matter world, such as the trapping of N-species with N > 2 in a system^[5] and the trapping of two component species experiencing different external potentials.^[6] In this paper, we are interested in the latter situation, which provides a testing ground for studying the competing effects of the external potential imbalance and the attractive interactions.

In the cold atomic experiments, a confining potential is necessary for trapping the atoms. For the theoretical research on most of the systems of cold atomic mixtures, the trapping potentials can be simply treated as the same for the different components, that is, the trapping potentials are component-independent. However, component-dependent external trapping potentials can be induced in the system of different hyperfine states or of different species with unequal masses, ^[7] where the different magnetic moments or the different masses make the trappings state- or species-dependent.^[8] A spin-dependent optical trap in the optical lattice can be realized by asymmetrically detuning the laser frequencies with respect to the different components.^[9]

The phase separation was studied by the mean-field theory due to the imbalanced mixture, paring symmetries, and antiferromagnetic order, ^[10] by the density-functional theory in a continuous system, ^[11] by the density-matrix renormalization group (DMRG) method^[12] in a lattice system due to the component-dependent external potentials and the repulsive interactions, ^{[13, 14]} and the polarizations.^[15] We focus here on the optical lattice system of attractive interactions, ^{[16– 18]} where the Fulde– Ferrell– Larkin– Ovchinnikov (FFLO) phase is one of the fascinating phenomena interested by both the experimentists^[19] and theorists.^{[20, 21, 23– 26]}

In this paper, we study the interplay between the trapping potential imbalance and the attractive interactions in a two-component Fermi gas loaded in the one-dimensional (1D) optical lattices, ^{[22, 27]} described by a Fermi– Hubbard model under the component-dependent external potentials. Contrary to the system under component-independent external potential, where the attractive interaction favors the FFLO phase, we find that in the present situation, the FFLO phase is easily destroyed by the attractive interaction, and as a result, the normal polarized phase or the BCS phase emerges.

The remainder of the paper is organized as follows. In Section  2, the model and the phase diagram are introduced. We present our numerical results and discussion in Section  3. Finally, we summarize our results.

In order to investigate the interplay between the external potential imbalance and the attractive interactions, we consider a two-component short-range interacting Fermi gas described by an inhomogeneous Fermi– Hubbard model

where 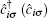is the creation (annihilation) operator with spin σ at site i, n̂ _iσ is the spin-σ particle number operator, t_σ is the hopping strength between the nearest-neighbor sites for component σ , L is the lattice size, U < 0 is the on-site attractive interaction strength, and V_σ describes the strength of the spin-dependent harmonic trapping potentials (in the following, we will refer the different hyperfine states or the different components as pseudospins σ ). This 1D single-band Hubbard model can be realized by trapping a two-component Fermi gas of different masses in a deep 1D optical lattice. For simplicity, in this paper, we discuss only t_↑ = t_↓ = t. We take the hopping parameter t to be the energy unit and use u = U/t. We also define a ratio between the spin-up and spin-down dependent harmonic trapping potentials to characterize the potential imbalance

The homogeneous 1D Fermi– Hubbard model of attractive interactions belongs to the universality class of Luther– Emery liquids of gapless charge excitations and gapped spin excitations, characterized by the fillings n_σ and the dimensionless coupling constant u. The inhomogeneous system with V_↑ = V_↓ at weak attractive interactions exhibits a compound phase characterized by the coexistence of spin pairing and atomic density waves. At strong attractive interactions, there is a state in which tightly bound spin-singlet dimers appear at the center of the trap.

We focus in this work on the spin-dependent potentials V_↑ ≠ V_↓ by applying the numerically exact DMRG techniques. During our DMRG simulations, the states kept are 600– 1000 so that the cut error is less than 10^{− 11}. We choose the balanced spin-up and spin-down atoms with the total number of particles N_s = 40 at a lattice of sites L = 100. Without loss of generality, we fix V_↓ /t = 0.001. Thus we vary γ (≥ 1) by increasing V_↑ /t to study the influence of the different trapping potentials.

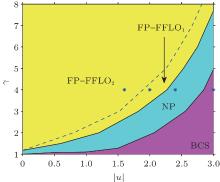
The ground-state phase diagram shown in Fig.  1 is our main result, which is a function of the external potential imbalance γ and the attractive interaction strength | u| . According to the density distributions and the pair– pair correlation functions, we find three different phase regions: a BCS phase at strong attractive interactions and small γ , a normal polarized (NP) phase in the intermediate parameter range, and the coexisted fully polarized phase and FFLO (FP-FFLO) phase of one (FP-FFLO₁) or two (FP-FFLO₂) peaks in the pair– pair correlation function.

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. Phase diagram as a function of the external potential imbalance γ and the attractive interaction strength | u| . There are three different phases: the BCS phase at strong attractive interactions and small γ , the normal polarized (NP) phase in the intermediate parameter range, and the coexisted fully polarized and FFLO (FP-FFLO) phase of one (FP-FFLO1) or two (FP-FFLO2) peaks in the pair– pair correlation function separated by the dashed line. The momentum pair distributions and the density profiles of the four different regions will be plotted in Figs.  3 and 4, respectively, the corresponding positions are designated by the four stars from left to right. The vertical axis corresponding to u = 0 belongs to the NP phase. The horizontal axis corresponding to γ = 1 is definitely the BCS phase.

Relying on whether the particle density difference Δ n_i = n_i↑ – n_i↓ vanishes (numerically we take | Δ n_i| ≤ 0.01) or not, we distinguish the BCS phase from the others. The FFLO phase can be judged from the pair– pair correlation function, where the momentum pair distributions show the peak at k ≠ 0. All the other cases give the NP phase.

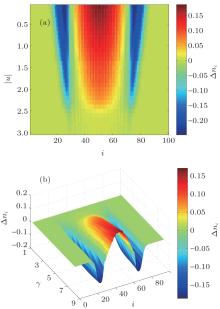
The density profiles in the experiment are measurable in the cold atomic system by the standard absorption imaging. In an array of 1D tubes of spin imbalanced ⁶Li atoms, the densities detected^[28] meet the criteria of the FFLO state predicted theoretically.^{[23, 24]} We plot the density difference Δ n_i = n_i↑ – n_i↓ as a function of the site i and the interaction strength u with γ = 4 in Fig.  2(a). The total number of particles is N_s = 40 with N_↑ = N_↓ , and the lattice size is L = 100. With the increase of the attractive interaction between the particles, we can find that both the spin-up and spin-down particles concentrate at the center of the trap, that is, the density difference becomes small, and eventually disappears around u = − 3. In this case, BCS pairing dominates, which will be clear from the calculation of the pair– pair correlation later. In Fig.  2(b), Δ n_i is plotted as a function of the site i and the ratio γ with the interaction strength u = − 2. We can see that with the increase of the external potential imbalance, the particle density difference gradually increases, which provides favorable conditions to form FFLO pairing. So for the strong attractive interactions and weak potential imbalances, Δ n_i = 0 elsewhere, signaling the BCS phase, while the increased potential imbalance makes the system polarized, and in this case, both the FFLO phase and the normal polarized phase are possible, depending on whether the finite momentum pairing dominates or not.

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. The contour or 3D plot of the density difference Δ ni = ni↑ – ni↓ (a) as a function of the site i and the interaction strength u with γ = 4 and (b) as a function of the site i and the ratio γ with the interaction strength u = − 2. The total number of particles is Ns = 40 with N↑ = N↓ , and the lattice size is L = 100. It shows that for the strong attractive interactions and weak potential imbalances, Δ ni = 0 elsewhere, which signals the BCS phase for the attractive case.

In order to further discuss the pairing properties, we calculate the pair– pair correlation function G(i, j), which is defined as

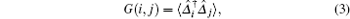with . We investigate the oscillatory character of the pair distribution function by studying its Fourier transform, that is, the momentum pair distribution given by

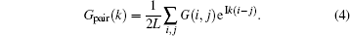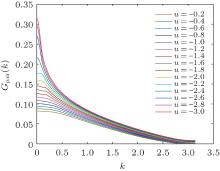
It is confirmed that for the attractive Hubbard model in a harmonic confinement (V_↑ = V_↓ ), the momentum pair distribution has a peak at the mismatch of the Fermi surface.^{[29– 31]} In Fig.  3, we show the momentum pair distributions for the four different regions of potential imbalance γ = 4 in Fig.  1. For the weak attractive interactions of u = − 1.6 in Fig.  3(a) and u = − 2.0 in Fig.  3(b), there is always a peak with a finite center-of-mass momentum (k ≠ 0), a phenomenon of the ground state being a 1D FFLO superfluid state with pairing at the two different Fermi surfaces induced by the imbalanced external potentials. For the system with two peaks, one at k = 0 and the other one at k ≠ 0, labeled by FP-FFLO₂, it is the mixed fully polarized phase (with a peak at k = 0) and FFLO phase (with a peak at k ≠ 0) but dominated by the polarized phase. The one with only one peak at k ≠ 0, labeled by FP-FFLO₁, is the FFLO dominated phase. In some parameter regions, the peak at k ≠ 0 is not clear, for example, in Fig.  4(b) for u = − 1.8. But if we get rid of the fully polarized region and focus on the center of the region, the finite momentum peak appears, as illustrated in the inset of Fig.  4(b).

Fig.  3.

	Figure Option ViewDownloadNew Window
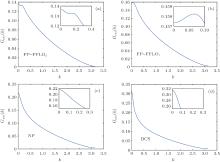	Fig.  3. The momentum pair distributions for the four different regions of potential imbalance γ = 4 in Fig.  1. The attractive interactions are (a) u = − 1.6 for the FP-FFLO2 phase, (b) u = − 2.0 for the FP-FFLO1 phase, (c) u = − 2.4 for the polarized normal phase, and (d) u = − 3.0 for the BCS phase. The inset magnifies the region around the peak.

Fig.  4.

Figure Option ViewDownloadNew Window

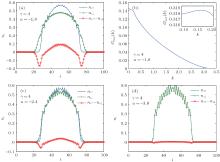Fig.  4. The density distributions (the full circle for ni↑ , the cross for ni↓ , and the full circle for Δ ni) for the three different phases of potential imbalance γ = 4 in Fig.  1. (a) The density distribution with u = − 1.8 for the FFLO phase of two peaks (FP-FFLO2). (b) The momentum pair distributions for case (a) in the center at i = 35– 64. The inset shows the magnified peak. (c) The density distribution with u = − 2.4 for the NP phase. (d) The density distribution with u = − 3.0 for the BCS phase.

By increasing the attractive interaction, both the spin-up and spin-down atoms accumulate towards the center of the trap. At first, the FFLO pairing is destroyed, and the normal polarized phase appears with an exponential decay in the pair– pair correlation function G_{i, j}, and its momentum pair distribution is depicted in Fig.  3(c). With a further increasing interaction, a slower power-law decay of quasi-long-range order in G_{i, j} appears, signalling a BCS phase, and its momentum pair distribution is shown in Fig.  3(d).

The density distributions for the three different phases of potential imbalance γ = 4 in Fig.  1 are also illustrated in Figs.  4(a), 4(c), and 4(d), for the mixed FP-FFLO phase, the NP phase, and the BCS phase, respectively.

The transition from between the BCS phase, the NP phase, and the FP-FFLO phase is a smooth crossover. We plot the momentum pair distributions at the fixed potential imbalance γ = 4 with varying attractive interactions from top u = − 3.0 to bottom u = − 0.2 in Fig.  5. When the attractive interaction u is small, the system is polarized with two different Fermi surfaces produced by the external potential. Depending on whether the FFLO pairing or the normal phase dominates, one peak at k ≠ 0 or two peaks at k = 0 and k ≠ 0 appear. When u ∼ 2.2, the FFLO dominated pairing is most obvious. With the increase of the attractive interaction u, the pairing mechanics of the particles is unfavored. The G_pair(k) has only one peak at k = 0 by forming the normal polarized phase or BCS pairing. As a result, an important observation is that the attractive interaction here destroys the FFLO pairing, contrary to the previous studies on the system of spin-independent external potential, where for a certain polarization, the stronger attractive interaction, the more stable the FFLO phase.^{[29– 31]}

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. The momentum pair distributions for the potential imbalance of γ = 4 with varying attractive interactions (from top u = − 3.0 to bottom u = − 0.2). A smooth crossover from the BCS phase, NP phase, to FP-FFLO phase occurs.

In this article, we show how the potential imbalance and the attractive interaction influence the phases of the one-dimensional fermionic Hubbard model under the spin-dependent external potentials. We find by using the DMRG technique that the FFLO pairing can appear even in the spin balanced system due to the polarization induced by the potentials, which leads to two different Fermi surfaces. For a fixed potential imbalance, when the attractive interaction is weak, a coexisted fully polarized and FFLO (FP-FFLO) phase of one peak at k ≠ 0 (named FP-FFLO₁) or two peaks at k ≠ 0 and k = 0 (named FP-FFLO₂) in the pair– pair correlation function appears, depending on whether the FFLO phase or the fully polarized phase is dominated.

Contrary to the previous studies on the system of spin-independent external potential, where for a certain polarization, the stronger attractive interaction favors the more stable FFLO phase, an important observation in this research is that the stronger attractive interaction breaks the FFLO pairing. At larger attractive interactions, when the FFLO phase is destroyed, the normal polarized phase is induced with an exponential decay in the pair– pair correlation function. At sufficiently large attractive interactions, both the spin-up and spin-down atoms are attracted towards the center of the trap, a BCS phase is induced with zero spin density difference and a power-law decay in the pair– pair correlation function.

The flexibility of the cold atomic experiments enables the possibility of realizing such a spin-dependent external potential and thus provides an ideal test bed for realizing a FFLO superfluid state in a 1D lattice. Detecting the FFLO phase in this system is possible with the standard absorption imaging or the magnetic structure factor for the quantum polarization spectroscopy signal.^{[28, 31]}