† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11474155, 11774147, 11674236, and 11922506).
Microtubule self-organization under mechanical and chemical regulations plays a central role in cytokinesis and cellular transportations. In plant-cells, the patterns or phases of cortical microtubules organizations are the direct indicators of cell-phases. The dense nematic pattern of cortical microtubule array relies on the regulation of single microtubule dynamics with mechanical coupling to steric interaction among the self-organized microtubule crowds. Building upon previous minimal models, we investigate the effective microtubule width, microtubule catastrophe rate, and zippering angle as factors that regulate the self-organization of the dense nematic phase. We find that by incorporating the effective microtubule width, the transition from isotropic to the highly ordered nematic phase (NI phase) with extremely long microtubules will be gapped by another nematic phase which consists of relative short microtubules (NII phase). The NII phase in the gap grows wider with the increase of the microtubule width. We further illustrate that in the dense phase, the collision-induced catastrophe rate and an optimal zippering angle play an important role in controlling the order–disorder transition, as a result of the coupling between the collision events and ordering. Our study shows that the transition to dense microtubule array requires the cross-talk between single microtubule growth and mechanical interactions among microtubules in the active crowds.
Dense ordered cortical microtubule (CMT) arrays is widely found in the interphase of plant cell.[1–3] The array structure is known to further dictate the direction of cell expansion. It plays a key role in consequent plant cell morphogenesis.[4–7] To understand the self-organization principle, in vivo fluorescent image reveals significant microtubule interaction during the polymerization process.[8–12] It has been shown that the steric interaction between microtubules will lead to zippering into microtubule bundles if they encounter each other at shallow angle. If they encounter each other at large angle, the blocked microtubules may stop growing, or crossover by protruding to the third dimension, and in some cases even induce dynamic catastrophe triggering fast depolymerization.[10,11] These dynamic processes are shown to be critical in leading to the formation of ordered dense microtubule array.[11,13–15] Furthermore, more and more microtubule associated proteins have been identified to reveal how these ordered microtubule arrays might respond to the external mechanical, geometrical, and chemical signals.[8,12,16–24]
These experimental findings inspire intensive studies on the self-organization of the microtubule array both numerically and theoretically, which leads to a general physical picture of ‘survival-of-the-aligned’ mechanism.[13–15,25–30] In these models,[14,25] microtubules are attached to cell cortical membrane in 2D and undergo polymerization and elongation during the formation of interphase microtubule array. Frequent collisions, zippering, and catastrophe events finally punish those discordant microtubles, and let the concordant ones survive long enough to self-organize into an ordered state.[30]
Detailed calculations provide a basic understanding of the order–disorder transition and the governing process.[15,14] Computer simulation thus turns out to be an efficient tool not only to illustrate the underlying ordering mechanism, but also for the illustration of possible rules guiding the organization process with the assistance of microtubule associated proteins.[14,15,18,21,25–27,30–35] For the simplest situation, it has been shown that simple mechanical-growth coupling is enough for the formation of ordered microtubule array. The regulation of cortical microtubule nucleation/polymerization/depolisymerizaiton is essential for the order–disorder transition in such system. In simulations, the role of microtubule associated proteins, such as katanin, etc., can also been taken into account.[17,30,31] Detailed dynamic regulations can be well captured by computer simulations and studied in a systematic way. Interesting factors like the topology of the cell compartment and 3D geometries can also be taken into account,[18,24,34] which further reveals the importance of mechanical constraints on the regulation of microtubule array morphology.
In this paper, following the spirit of previous minimal model, we use computer simulations to study the possible effects of surface crowdedness on the self-organization of microtubule array in 2D. Microtubules are closely attached to the plant cell membrane, where various cellular activities and regulations take place.[1,2,6] In vivo, in such crowded condition, the decoration of microtubule associated proteins, motors, and cell membrane substrate, and even the screened electrostatic interaction might change the effective width of the microtubule and their inter spacing.[36–45] Previous models also show that without the inclusion of microtubule width, the microtubules may self-organize into a dense ordered array.[14,15,30] To address the effect of crowdedness, we have to take into account of the effective width of microtubules. We find that by introducing such an intrinsic geometry property, it can qualitatively change the phase behavior of the system. The additional crowdedness delays the order–disorder transition, and leads to an intermediate phase, which has only been observed in the very dense regime in a model with zero width.[15] The inclusion of microtubule width may further change the consequent collision relevant events, such as collision induced catastrophe and zippering.[11] These mechanical-growth couplings are incorporated in simulation to reveal how the plant cell might be able to regulate the mechanical response with optimal critical zippering angles.
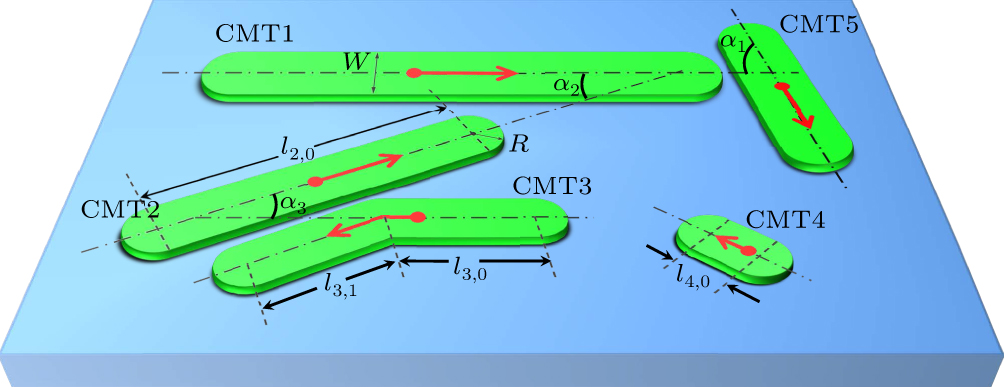
Here we model microtubules with a finite width in order to properly account for the exclude volume interaction in the dense phases of cortical microtubule array. With high growth rate, a line segment model with zero width may lead to ultra-high density. The effective width of microtubule thus plays an important role to regulate microtubule density in such phases. A schematic illustration of the model is shown in Fig.
Following previous studies, at present coarse-grained level, the single microtubule dynamics are sufficiently described by the growth/catastrophe/shrinkage/rescue on the plus end of the microtubule and shrinkage on the minus end.[25,46,47] The growth speed kg on the plus end is usually larger than the shrink speed ksm on the minus end, otherwise the microtubule cannot exist for long time. The catastrophe rates on the plus end can be distinguished by spontaneous catastrophe rate ksc and collision induced catastrophe rate kic. In the dilute limit, since collisions among microtubules are rare, we can expect that spontaneous catastrophe is more dominant than induced catastrophe.[48,49] But here, since we are interested in the dense phase, collision happens so frequently that the induced catastrophe may dominate the catastrophe events.[50] The catastrophe events will lead to the shrinkage of microtubule ks on the plus end. Microtubules can resume growth with a rescue rate kr. The typical values of the kinetic parameters used in the simulations are listed in Table
| Table 1. List of parameters and values in the simulation. . |
During the growth, the microtubules may encounter each other. The growth of blocked microtubule will be stopped since no free space is available for the addition of a new segment. Microtubules are quite rigid, with typical persistence length of several millimeters.[51] The small flexibility still allows it to deviate its original growth direction. In experiment, the so called zippering events are observed when two microtubules encounter, or even crossover if microtubule growth into the third dimension out of the plane.[11,50] For simplicity, here we restrict ourselves to strictly 2D, thus we do not consider the crossover events. For zippering, it has been observed that such event depends on the relative angle α between colliding microtubules.[11,52] We can define a critical α0 to approximate the angular dependence. If the collision angle α>α0, zippering is not possible. If the system allows induced catastrophe, then such large angle encounter would trigger such event with a rate kic. For α < α0, zippering will take place, and the colliding microtubule changes its growth orientation following the direction dictated by the encountered microtubule (see Fig.
We apply the event driven Gillespie algorithm to simulate our mechanical–chemical coupled dynamic system.[29–31,53] In each simulation step, the time is forwarded according to 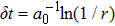
The order of the system can be measured according the magnitude of weighted nematic order parameter tensor as defined in Refs. [15,30], which is given by
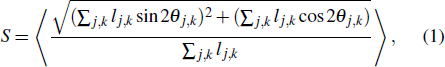
To see how the collective behavior of the dense microtubule array may be affected by the effective microtubule width and other dynamic processes, in the following sections we first use a simple tread milling model where the critical angle α0 for zippering is set to 0°, and neglect catastrophe events on the plus-end of the microtubule. Next, we switch on the spontaneous and induced catastrophe events and demonstrate their relative importance in controlling the order–disorder transition. Finally, we vary the critical zippering angle α0 and show the optimal regime to achieve nematic order.
To simulate crowded cortical microtubule array, we have to take into account of the effective width of single microtubule in the model. In vivo, the effective width of microtubule may differ from that of bare microtubule due to the complicated cortical environment and electrostatic interactions. First microtubules are strongly attached to the cell membrane, thus the membrane and associated proteins may mediate the effective interaction among microtubules. Moreover, the decoration of microtubule associated proteins may also change the effective width directly. In Fig.
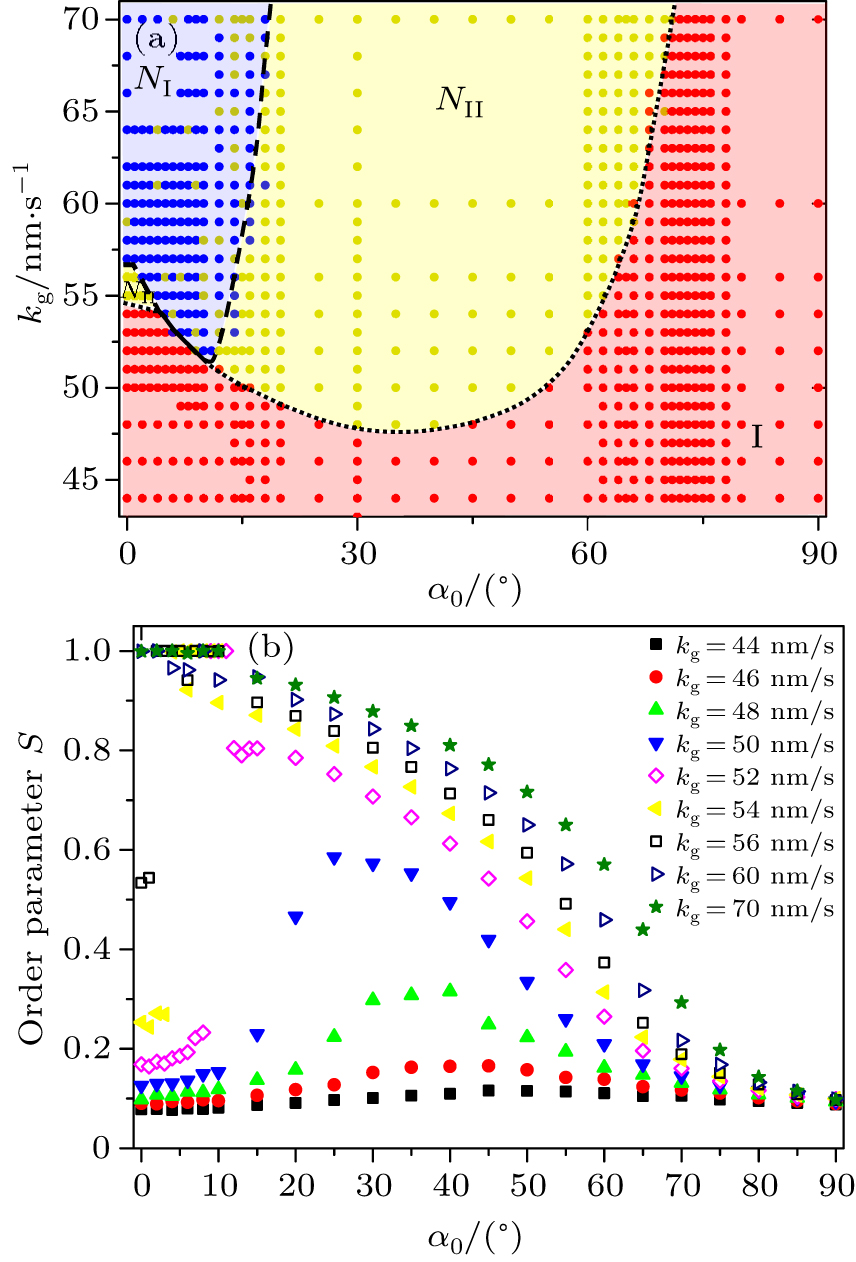
Although the symmetry of the NII and NI phases is the same, the transition between these two phases is usually discontinuous (first order-like), thus they could be well distinguished by studying how order parameter S varies with the control parameters. Here, we choose to fix the effective width W = 0 nm and W = 25 nm and increase the polymerization rate kg so that we can expect a direct transition from isotropic phase I to NI phase at W = 0 nm, and an intermediate transition into NII phase at W = 25 nm. We measure order parameter S as defined in Eq. (
As a result, in the phase diagram of Fig.
With the inclusion of the effective width, we now check how the catastrophe events will be coupled to the finite width microtubule system. The collision induced catastrophe depends on the blocked configurations among growing microtubules. In the dilute limit of the microtubule system, with negligible collisions, the spontaneous catastrophe plays much important roles. It regulates the length distribution and thus also the order property of the system. In the dense phase, the induced catastrophe becomes much important due to the frequent collisions among microtubules. We are interested here to see how different catastrophes may effect the self-organization of the dense phase.
For this purpose, we choose W = 25 nm (approximately the bare width of microtubule) and kg = 70 nm/s with rescue rate kr = 0.01 s–1 (see Table
Since kic needs the collision process to trigger the catastrophe, its value does not represent the frequency of catastrophe events that actually take place in the system. We can further compare the effects of both catastrophes by the frequency of real catastrophe events (RCEs). We count the average frequency of RCEs in simulations for both cases in steady state. The statistics are shown in Fig.
There are two important features in such representation. First, compared with Fig.
Second, for given RCEs, the induced catastrophe still demonstrates significantly higher nematic order than the case for spontaneous catastrophe. The spontaneous catastrophe events only depend on the number of microtubules that are in the growth state, as we can see from the term kscN+ in Eq. (
Zippering also depends on the collision among microtubules. In an active dense phase, we expect it would play an important role in controlling the order–disorder transition. One important parameter controling the zippering events is the critical angle α0. When the colliding angle α is less than α0, two microtubules will zipper. However, when colliding angle α is larger than α0, we expect it is going to block the growth, and even can trigger collision induced catastrophe or crossover events. As we show above, catastrophe events basically are going to reduce the order in the system monotonously. Its effects can be compensated by increasing the growth speed. Here to investigate the effect of zippering, we set catastrophe to 0 s–1. We also restrict ourselves strictly in 2D, thus do not consider the crossover events.
Zippering is considered a promotion effect of order in the system.[11] It helps to change dis-aligned microtubule groth along with their neighbor thus effectively introduces an alignment interaction. On the other hand, if zippering can happen very easily for large α, the microtubules essentially become very flexible. For flexible polymer, nematic order will disappear. To compromise the easiness of alignment and rigidity, we may expect an optimal critical zippering angle α0 for nematic alignment.
In Fig.
The optimal zippering angle indicates that zippering does not simply enhance the alignment. Although it enables the alignment of the growth direction of microtubules, it leaves those dis-aligned segments unchanged. Such dis-aligned segments can only be eliminated by depolymerization on the minus end. The catastrophe events on the plus-end would not help since it starts from the plus end and will eliminate the aligned part first. For large α0, the zippering events happen irrespective of the colliding angle, which leads to frequent large angle bending of microtubules and drives the system into complete disorder.
In our simulation, by systematically varying the critical zippering angle α0, we find optimal zippering angle around 30° to 40° for NII phase. This optimal angle is consistent with the experimental determined zippering value. In vivo, various conditions may help regulating the critical angle for zippering. Since microtubules have large persistence length, the most important factor in control might be the microtubule associated proteins that fastens the microtubule on the cell cortex.[36,44,54] Higher density of these binding proteins might allow small critical zippering angle. Moreover, the plus-end microtubule associated proteins might also play a role in the regulation of zippering. It would be interesting to investigate if evolution has allowed plant cell to exploit such possibility to do optimization for achieving ordered cortical microtubule array.
Through computer simulations, we incorporate the effects of effective width of cortical microtubule, the induced catastrophe events, and zippering effects to investigate the phase behavior in self-organized crowded microtubule array. We show that in the dense phase, the finite volume of microtubule plays an important role in regulating the order–disorder transition. It significantly enhances the probability of mutual blockage of microtubule growth, thus at finite density it is able to confine the growing microtubule length and suppresses the system into relatively lowly ordered NII phase. With less free space it also triggers more collision induced catastrophe and zippering events, all these will further regulate the phase behavior of the microtubule array.
In the dense phase, we expect that the collisions among microtubules are frequent, thus the collision induced catastrophe and zippering of microtubules will become important. On the other hand, the dense phase usually corresponds to highly ordered nematic state.[55] The mutual alignment significantly reduces the collision process. These effects are revealed in our simulation, where we find in NI phase the collision induced catastrophe rate is very low. Since the rate of collision induced catastrophe may change with the modification of local configuration, it will enhance the establishment of nematic order from a disordered state. First it will eliminate misaligned microtubules since these microtubules will trigger frequent catastrophe event if growing. Second, once microtubules are aligned, the induced catastrophe is dramatically reduced and locks the system in the ordered phase.
Our simulations show that the zippering mechanism is unexpectedly important in regulating the order formation in such dense microtubule array. Experimentally confirmed zippering critical angle is found to be optimal for the emergence of NII phase. For small growth rate, both small and large zippering critical angles α0 may lead to disorder. Our results suggest that the microtubule associated proteins that attach microtubules onto cell cortex will play an important role in regulating the critical zippering angle as observed in vivo.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] |