† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant Nos. 2017YFA0304401, 2018YFA0307500, 2017YFA0304404, and 2017YFF0212003), the National Natural Science Foundation of China (Grant Nos. 11622434, 11774388, 11634013, 11934014, and 91736310), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB21030100), the CAS Youth Innovation Promotion Association (Grant Nos. Y201963 and 2018364), and the Science Fund for Distinguished Young Scholars of Hubei Province, China (Grant No. 2017CFA040).
Progress of the 40Ca+ ion optical clock based on the 42S1/2 – 3d 2D5/2 electric quadrupole transition is reported. By setting the drive frequency to the “magic” frequency Ω0, the frequency uncertainty caused by the scalar Stark shift and second-order Doppler shift induced by micromotion is reduced to the 10−19 level. By precisely measuring the differential static scalar polarizability Δα0, the uncertainty due to the blackbody radiation (BBR) shift (coefficient) is reduced to the 10−19 level. With the help of a second-order integrating servo algorithm, the uncertainty due to the servo error is reduced to the 10−18 level. The total fractional uncertainty of the 40Ca+ ion optical clock is then improved to 2.2× 10−17, whereas this value is mainly restricted by the uncertainty of the BBR shift due to temperature fluctuations. The state preparation is introduced together with improvements in the pulse sequence, and furthermore, a better signal to noise ratio (SNR) and less dead time are achieved. The clock stability of a single clock is improved to 
Owing to their low uncertainty and instability, atomic optical frequency standards have found many irreplaceable and extremely important applications, such as in navigation and for tests of physical theories that need high precision. In the past two decades, the development of optical clocks has made great progress, surpassing the microwave Cs fountain clocks in terms of uncertainty and stability.
Optical frequency standards are mainly based on single ions trapped in ion traps such as Ba+, Sr+, Hg+, In+, Al+, Yb+, and Ca+, [1–5] or neutral atoms trapped in optical lattices such as Sr, Yb, and Hg.[6–10] Single-ion optical clocks always have simple ion-trap and optical systems as a single ion can be confined by a radio frequency (RF) potential for as long as several days or even a month. To date, the Al+ ion of NIST has achieved the smallest uncertainty of 9.4× 10−19.[11] Optical lattice clocks can provide better stability because of their large number of atoms. Benefiting from the development of the ultra-narrow-linewidth laser technology, the Sr lattice optical clock in JILA has achieved the best stability of 

The optical clocks based on the 42S1/2–3d 2D5/2 electric quadrupole transition of a single trapped 40Ca+ ion have been studied by our group at the Wuhan Institute of Physics and Mathematics (WIPM), Chinese Academy of Sciences in China for many years. The reason why we chose the 40Ca+ ion is its relatively simple energy level structure and laser system in which all lasers mentioned in the energy-level scheme (Fig.
 | Fig. 1. Partial energy-level diagram of 40Ca+ showing the transitions used in cooling, repumping, and probing. |
For optical clocks, the most important criteria are low uncertainty and instability. In 2015, we achieved an uncertainty of 6.5 × 10−16 and a stability of 

The 40Ca+ ion optical clock system mainly consists of two parts. One is the ion trap system, containing an ion trap, a vacuum chamber, magnetic shields, and fluorescence detection devices. The other is a laser system, for the 40Ca+ ion, which is composed of 397-nm, 866-nm, 854-nm, and 729-nm lasers and their frequency-stabilization devices.[7]
In 2015, we used a miniature Paul ring trap to trap a 40Ca+ ion. To reduce the shift and its uncertainty due to the secular motion, an ion trap with a lower heating rate is required. A new trap originally designed by NIST[11] with small modifications is adopted. A schematic diagram of this trap is shown in Fig.
As shown in Fig.
In this work, the improvements on the pulse sequence mainly focus on a reduction in dead time and the introduction of state-preparation technology. The new control system based on the FPGAs and DDSs can alter the RFs applied to the AOMs within a few microseconds. Then, we can change the frequency and power of the cooling laser beam many times within one cycle to realize optimal cooling and fluorescence-detection efficiency simultaneously. The dead time caused by modifying all RFs is negligible. Moreover, with the implementation of the state preparation nearly double the previous excitation probability on the resonance of the clock transition can be achieved, which means a lower instability.
Figure
As shown in Fig.
For the 40Ca+ ion, the ground state 2S1/2 has two magnetic sublevels with equal probability, so the greatest excited probability for each Zeeman component is only ∼ 0.5, as there is only a 50% chance that the ion is in the 2S1/2(m = +1/2) or 2S1/2(m = –1/2) states initially. Initial state preparation can increase the transition probability twice and improve the stability by 
In the interrogation, other lasers, except for the probe laser, have been switched off by mechanical shutters instead of the AOMs to cancel other lasers’ AC Stark shift.[14,21] It adds a 5-ms-long dead time twice, for opening or closing the mechanical shutter before or after the integration, respectively. In this experiment, the two clocks share the same clock laser and timing control system, i.e., for the two clocks, the interrogation is asynchronous. To improve the stability compared to the previous result,[13] we choose the Ramsey scheme with which a single π-pulse is separated equally by a free evolution time Tfree. For a sufficiently short pulse duration, the linewidth of the central fringe is independent of the Rabi pulsation and is equal to 1/2Tfree.[6] This is much narrower than the Rabi result on the condition of the same time spent in the interrogation.
For a single ion system, to obtain the transition probability at each frequency point, the ion needs to be interrogated multiple times with the same parameters, and the successful excitations will be counted. For the 2S1/2 → 2D5/2 transition, if the ion is found in the 2D5/2 state by detection after interrogation, it has been excited successfully.[22] Thirty integrations at each frequency point were taken, and a Ramsey spectrum with a free evolution time of 80 ms is obtained, as shown in Fig.
A variety of potential sources might be associated with the 2S1/2 → 2D5/2 electric-quadrupole transition of a laser-cooled trapped 40Ca+ ion, causing a frequency shift and uncertainty. They have been evaluated in our previous work.[14,21] In this paper, we report the recent progress on the evaluation of the scalar Stark shift and the second-order Doppler shift induced by excess micromotion, the BBR shift, and the servo shift.
Figure




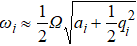
If we consider a uniform static electric field Edc, equation (


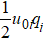
Ion movement can create a second-order Doppler (time-dilation) shift and a scalar AC Stark shift due to the AC field the ion experiences. If we consider only the shifts caused by the excess micromotion, they are approximately[3,15,23]

From Eqs. (


The experiment of measuring the frequency Ω0 is based on the comparison of two clocks (clock 1 and clock 2). Clock 1 is used to provide a constant standard frequency reference, and clock 2 is a test trap to study the change in micromotion shifts with trap drive frequency Ω. To begin with, all indicators of frequency shift and uncertainty of both clocks were optimized to the best with a fractional frequency uncertainty of ∼ 3× 10−17. We can guarantee that the transition frequency of clock 1 is a constant value within the uncertainty level, and that any frequency change exceeding the uncertainty level of clock 2 is entirely caused by micromotion. The DC offset voltage of clock 2 is trimmed to induce a relatively large micromotion level in the ion for an obvious comparison. Then, the frequency difference of the two clocks is due to the micromotion shift of clock 2. The drive frequency of clock 2 is tuned from 22 MHz to 27 MHz and the frequency difference at each point was measured, as shown in Fig.
 | Fig. 9. Frequency difference between the two 40Ca+ ion clocks as a function of the RF drive frequency of clock 2. The red curve is a fit to the data and gives Ω0 = 2π × 24.81(1) MHz. The shaded area illustrates the uncertainty in the theoretical result.[15] |
To obtain the value of Δα0 with a lower uncertainty by Ω0, we have to consider the micromotion at the trap drive harmonics nΩ. The total scalar Stark shift and the time-dilation shift can be expressed as[3,15]

To date, the BBR shift uncertainty is the main source of the total uncertainty for the 40Ca+ ion.[24] The BBR shift of the S–D transition can be expressed as[25–27]

In contrast to optical lattice atomic clocks, a single interrogation of a single ion can only provide one binary unit of information. In one frequency feedback cycle, the ion should be interrogated multiple times on the two sides of each Zeeman component to obtain the transition probabilities or error signal. The probe laser’s frequency is f and the ion is interrogated n times at the frequencies of f+ = f + δm/2 and f− = f – δm/2 respectively, where δm is the linewidth. After counting the successful excitations n+ at f+ and n– at f–, the error signal and the frequency modification of the probe laser can be expressed as follows:[16,22]


Generally, the frequency of the clock laser is subject to drift with a nonlinear rate, similar to the probe laser between each frequency modification. However, for an ion optical clock, each feedback takes about a few seconds or more. The probe laser’s frequency may change significantly and randomly owing to the noise of the reference cavity. This will cause a significant servo shift and error. A second-order integrating servo algorithm is introduced to obtain the current drift rate by the analysis of the latest frequencies, which reduces the servo error[14,16,28]


Benefiting from the implementation of a second-order integrating servo algorithm and a longer probe time, the servo-error uncertainty is reduced to 7.6× 10−18.[15]
Table
| Table 1. System shifts and uncertainties for the evaluation of the 40Ca+ ion.[5] . |
Stability is an important criterion for optical clocks besides uncertainty. To measure the frequency stability of a 40Ca+ ion optical clock, we compared the frequency difference between two independent clocks continuously for approximately 38 h. In this experiment, both clocks have independent physical and optical systems, except for the probe laser, which is stabilized by a 10-cm-long ULE cavity.[7] Both 40Ca+ ions are interrogated asynchronously. To cancel the electric quadrupole shift and quadratic Stark shift, we lock the probe laser to two pairs of the Zeeman components.[14,29] One pair is 2S1/2(m = +1/2) → 2D5/2(m = +1/2) and 2S1/2(m = –1/2) → 2D5/2(m = –1/2), and the other is 2S1/2(m = –1/2) → 2D5/2(m = –3/2) and 2S1/2(m = +1/2) → 2D5/2(m = +3/2). The pulse sequence is shown in Fig.
The center frequency of the 2S1/2 → 2D5/2 transition for the 40Ca + ion can be computed by the frequencies of the four Zeeman components[14,30]
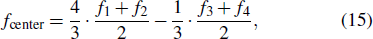

 | Fig. 10. Measurement of Ω0 obtained by scanning the RF drive frequency of clock 2. To reduce the measurement statistical uncertainty of Ω0, we repeated this scanning randomly from 24.7 MHz to 24.95 MHz 15 times. Fifteen scans were recorded (data shown as black squares). The corresponding weighted mean of Ω0 is shown by the red circle. The inset shows the data taken in one of the scans and a linear fit through the data as shown in Fig. |
To improve the performance of the 40Ca+ optical clock, several efforts have been made in recent years. For the uncertainty, we precisely measured the “magic” trap drive frequency Ω0 at which the shift of the scalar Stark and second-order Doppler induced by excess micromotion can cancel each other, corresponding to an uncertainty of below 1× 10−18. Then, the differential static scalar polarizability Δα0 is obtained by using the measured “magic” trap drive frequency Ω0, with an uncertainty about 40 times smaller than the value of the theoretical calculation. Benefiting from the more accurate value of Δα0, the uncertainty due to the BBR shift (coefficient) has also been evaluated to be 3× 10−19. Additionally, the servo error uncertainty is also reduced to the 10−18 level by introducing a second-order integrating servo algorithm. Finally, the total uncertainty of the 40Ca+ ion optical clock is evaluated to be 2.2× 10−17. For stability, we increased the pulse length to 80 ms and obtained a high-resolution Ramsey spectrum with a linewidth of approximately 6.5 Hz. The time spent on cooling and detection has been reduced significantly by changing the frequency of the cooling laser on the precooling, Doppler, and detection pulses. Furthermore, by preparing 40Ca+ ion in one of the two ground states, the transition probability is double than before, which greatly reduces the QPN. With these improvements, the Allan deviation is measured to be 
For the BBR shift due to temperature fluctuations, according to Eq. (
The stability of the 40Ca+ ion optical clocks is ultimately limited by its metastable state lifetime of 1.16 s.[31] For Rabi interrogation, this limit is 
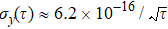
Lower instability for single-ion optical clocks can be obtained by a longer probe time, which will be adopted in the future, with the help of a lower frequency noise by the clock laser and a shorter dead time.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |













