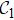† Corresponding author. E-mail:
Project supported by the National Key R&D Program of China (Grant No. 2017YFA0304203), the National Natural National Science Foundation of China (Grant Nos. 11604392 and 11674200), the Changjiang Scholars and Innovative Research Team in Universities of Ministry of Education of China (Grant No. IRT 17R70), the Fund for Shanxi “1331 Project” Key Subjects Construction, and the 111 Project, China (Grant No. D18001).
We present a protocol to realize topological discrete-time quantum walks, which comprise a sequence of spin-dependent flipping displacement operations and quantum coin tossing operations, with a single trapped ion. It is demonstrated that the information of bulk topological invariants can be extracted by measuring the average projective phonon number when the walk takes place in coherent state space. Interestingly, the specific chiral symmetry owned by our discrete-time quantum walks simplifies the measuring process. Furthermore, we prove the robustness of such bulk topological invariants by introducing dynamical disorder and decoherence. Our work provides a simple method to measure bulk topological features in discrete-time quantum walks, which can be experimentally realized in the system of single trapped ions.
Topological physics, which exhibit some of the most striking phenomena in modern physics, have been investigated intensively in recent years.[1–3] Contrast to the conventional phases characterized by local order parameters, the bulk topological phases are distinguished by topologically invariant integers.[4] Classification and detection of bulk topological phases give an essential understanding of topological physics. In addition, the novel bulk topological features have potential important applications in quantum information for their robustness. Besides condensed-matter materials such as topological insulators and superconductors, topological phenomena also emerge in synthetic systems such as photonic systems[5–7] and cold atoms in optical lattices.[8] Moreover, recent progress has focused on the measurement of bulk topological invariants of these synthetic systems.[9–14] The flexibility offered by these synthetic simulators guarantees the exciting possibility of extending the study of topological matters to regimes beyond the scope of the condensed-matter physics based on electronic systems.
An outstanding example here is the identification of topological phenomena in discrete-time quantum walks (DTQWs), in which the movement of the particle (walker) on a lattice depends on the specific internal (coin) state.[15] The DTQW provides an unique platform to investigate all topological phases in one- and two-dimensional noninteraction systems with certain symmetries.[16,17] Over the past few years, it has become technologically possible to implement DTQWs in real systems using ultracold atoms in optical lattices,[18,19] trapped ions,[20,21] photons[22,23] and nuclear magnetic resonance.[24] Moreover, the topological effects, including the topological edge states, the topological phase transitions and the topological invariants, in the context of DTQWs have been widely discussed theoretically,[16,17,25–36] and experimentally measured by several groups.[37–51] For chiral DTQWs, the mean chiral displacement is proportional to the topological invariant in long-time limit.[39] For general DTQWs, the topological invariants can be obtained using scattering theory.[40] Furthermore, the topological invariants can also be directly extracted through the accumulated Berry phase of Bloch oscillating DTQWs in a circuit quantum electrodynamics (c-QED) architecture,[35,41] or through the winding number of a large-scale chiral DTQW.[42] Nevertheless, the direct measurement of these topological invariants is still a huge challenge for the experimental technology of tomography required by current experimental methods. Even the mean chiral displacement also requires the detection of all position states and the coin state at each lattice. Recently, a theoretical work proposed that the average photon number can be used to reveal the topological phases transition in a c-QED architecture, where a DTQW takes place in coherent state space.[52] The measurement of bulk topological invariants have also been discussed in this work, while it has no generality since the dependence of the initial coin state. In addition, all the above experimental progresses are based on photonic DTQWs, there are few studies on the topological features in other synthetic quantum systems.
In this paper, we propose an experimental protocol to realize topological DTQWs in coherent state space with single trapped ions. Through analytical and numerical analysis, we illuminate the topological structure of our DTQWs, including two pairs of topological invariants and the mean chiral displacements. More importantly, we demonstrate that the information of bulk topological invariants can be extracted through the average projective phonon number of the final state, with no need for reading out the position states and the coin state at each lattice. For completeness, we define two kinds of average projective phonon numbers corresponding to different parameter regions. By introducing dynamical disorder and decoherence, we verify the robustness of our results. This work gives a simple method to directly measure bulk topological invariants in discrete-time quantum dynamics in coherent state space.
This paper is structured as follows. In Section
The key problem of realizing DTQWs in real systems is how to implement a spin-dependent displacement operation. Here we implement a spin-dependent flipping displacement operation in coherent state space with a single trapped ion. Most of the previous works are concerned with the spin-dependent displacement operation without flipping. Only one experimental group considers a complicated spin-dependent flipping displacement operation, which is implemented by a special q-plate.[38,39] Although this seems like a small difference, it can have far reaching consequences with a simple chiral symmetry, as we will show in the following.
The spin-dependent flipping displacement operation is defined as

Firstly, we apply displacement Raman beams, the corresponding interaction Hamiltonian between the light field and the trapped ion in the interaction frame can be written as[53]



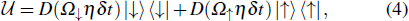
Secondly, a π pulse Rπ, which exchanges the two coin states, is required.
Finally, we apply displacement Raman beams again with opposite Rabi frequencies, the resulting evolution operator over time δ t is

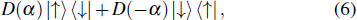

Based on the current ion-trap techniques,[20,21] it is possible to realize such a spin-dependent flipping displacement operation in the realistic ion-trap experiments. For example, the Rabi frequencies can satisfy 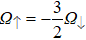
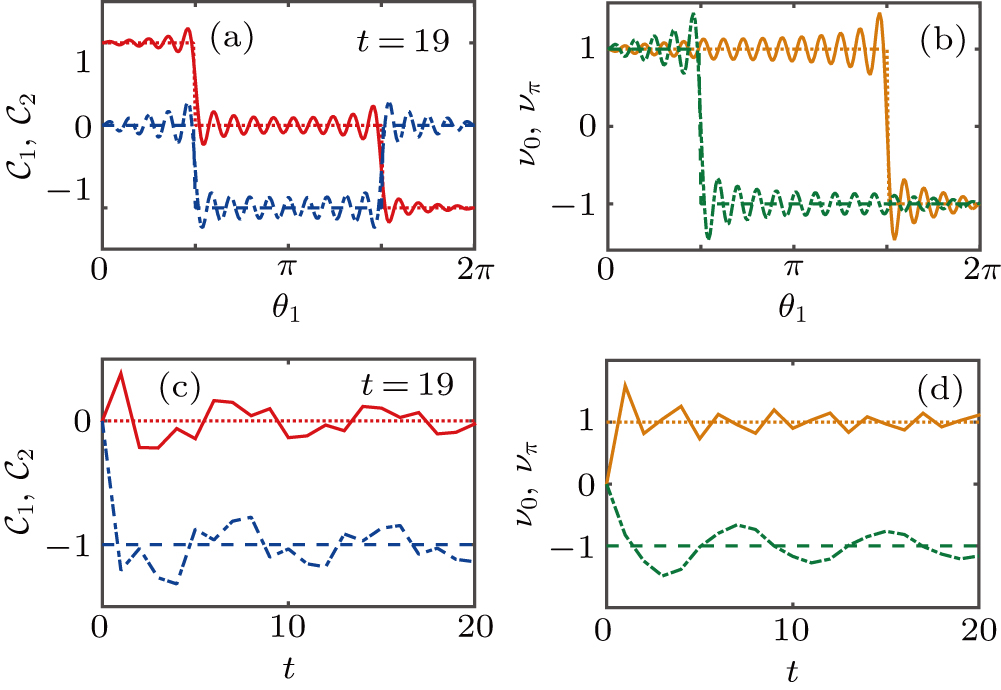
Since in Floquet 1D systems, there exists two independent classes of protected edge states at either 0 or π energies. A complete topological classification for such a system with chiral symmetry would require introducing a pair of topological invariants (ν0,νπ).[26] Thus, we consider two inequivalent “chiral symmetry time frames” of DTQWs as follows:

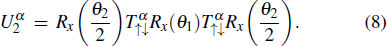
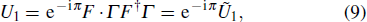






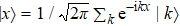

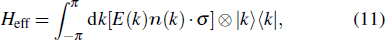

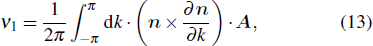
Without loss of generality, in the following discussion, θ2 is fixed to 3π/2 and θ1 ∈ [0,2π] when we consider the topological invariants varying with the rotation angle, the transition points are at θ1 = π/2 and 3π/2. We fix θ1 = π/4, 3π/4 and θ2 = 3π/2 when we consider the topological invariants as functions of the step t, see Fig.
From the previous research,[39] the topological invariants can be obtained through the mean chiral displacement



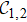

In Fig. 


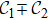
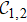

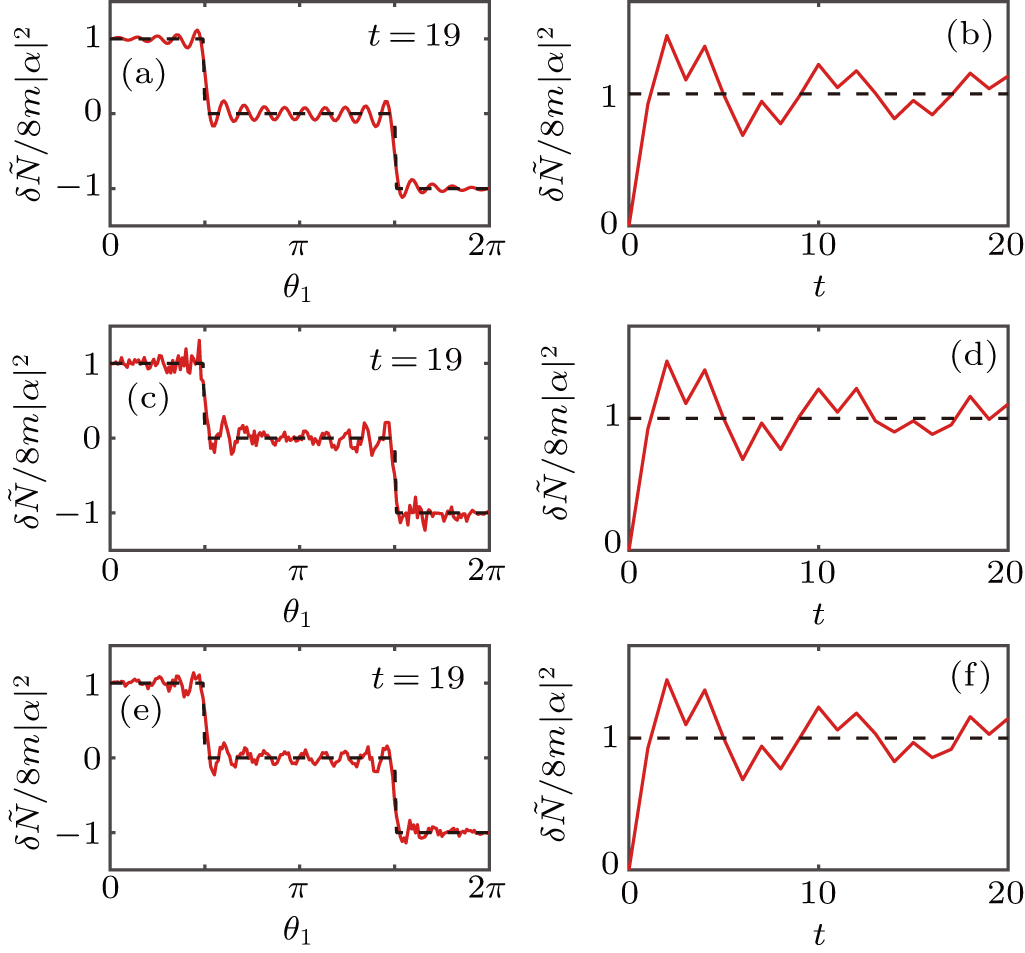
In ion-trap systems, the phonon number can be measured through Rabi flopping or blue-sideband driving,[53–55] and has been detected experimentally for revealing rich physical phenomena.[56–58] Here we illustrate that the information of bulk topological invariants can be extracted through the average projective phonon number of final state, which is convenient to measure in experiments. Since the following analysis are identical for these two DTQWs governed by 


Thus, the average projective phonon numbers can be written as

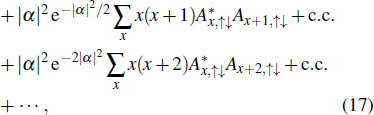

In the following discussions, we show the details about how to extract the information of the mean chiral displacement 
When |α| is large enough, the average projective phonon numbers have really simple expressions N↑↓ = |α|2Σxx2|Ax,↑↓|2, where only the first term in Eq. (
Thus, the average projective phonon numbers of these two DTQWs are



In Fig. 
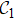

Furthermore, the novel topological features of a system are robust against small perturbations. Here, we verify the robustness of ΔN by introducing dynamical disorder and decoherence. For the situation with dynamical disorder,[39] the rotation angle θ1 is chosen randomly from the interval 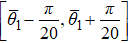
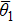
When |α| is small, the contributions of higher terms in Eq. (
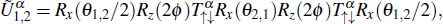



The average projective phonon numbers of the new final state have the form

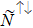


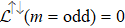
Here, we consider the second and fourth terms, ignoring the more higher terms. For extracting 

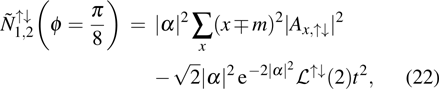


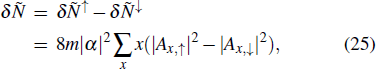

Using a numerical simulation, we demonstrate that the combination of the average projective phonon numbers 









In a realistic ion-trap experiment,[58] the phonon number can be detected varying with the interaction time. In other ion-trap experiments for realizing DTQWs,[20,21] the system can be detected at different steps of DTQWs. Thus, the measurement of the projective phonon numbers at different steps of DTQWs proposed in our scheme is possible in current ion-trap techniques.
In summary, we have proposed experimental protocols to realize topological DTQWs in the system of single trapped ion, where the walk takes place in coherent state space. We demonstrate that the experimental measurement of bulk topological features can be easily monitored through the average projective phonon number. No more experimental technologies for reading out all position states or tomography are required. In addition, the chiral symmetry owned by our DTQWs further simplifies the experimental measurement process. By introducing dynamical disorder and decoherence, we verify the robustness of our results. This work gives a simple method to directly measure bulk topological invariants using discrete-time quantum dynamics of in coherent state space.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] |