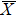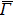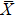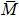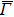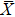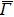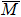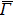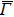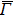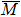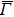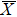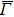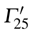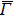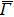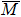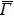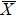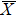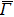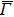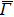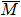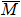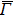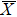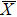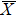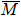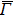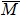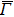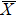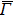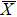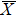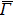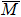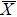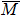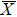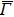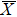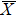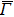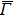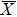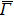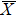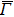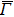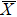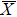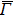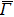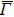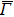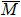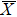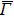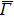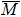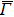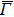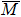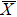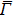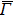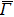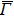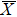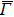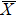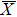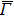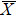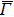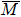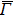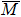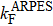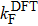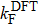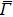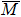High-resolution angle-resolved photoemission study of oxygen adsorbed Fe/MgO(001)
1. IntroductionThe metal–oxide interface is one of the most extensively investigated topics in the surface science.[1–4] The strong bonding between oxygen and metal atoms at the surface significantly modifies the crystallographic and electronic structures, which affects the transport and magnetic properties such as the tunnel magnetoresistance effect[5] as well as the catalytic reactions at the surface.[4,6] The p(1 × 1) oxygen adsorbed ferromagnetic Fe(001) surface is one of the prototypical systems for the metal–oxide interface and has been extensively studied for decades.[4,7–28] The adsorbed single layer oxygen atoms occupy the fourfold hollow sites of the Fe(001) surface and are situated on-top of the subsurface Fe atoms.[4] The structural studies of the Fe(001)–p(1 × 1)-O surface using the low-energy electron diffraction (LEED) and medium-energy ion scattering measurements clarified that the spacing between the topmost and second Fe layers (d12) was 1.54–1.55 Å[7,8] and 1.59 Å,[9] respectively. The obtained d12 was enhanced by 8%–11% compared with the bulk value 1.43 Å.[8] On the other hand, the distance between the oxygen atoms to the topmost Fe layer dO–Fe was evaluated to be 0.45 Å.[8] Recent surface x-ray diffraction study has elucidated d12 to be 1.66 Å, which is 16% larger than that in the bulk and dO–Fe is 0.48 Å.[10] The density functional theory (DFT) calculations on the oxygen adsorbed Fe surface have been carried out using a slab model.[11–15] Due to the strong bonding between the adsorbed O 2p and Fe 3d states, the d12 and magnetic moments of the first few Fe layers become larger than those in the bulk.[11–15] Previous angle-resolved photoemission spectroscopy (ARPES)[16–19] on Fe(001)–p(1 × 1)-O surface clarified the O 2p-derived states in the energy range of −4 eV to −9 eV well below the Fermi level (EF) and the momentum dependent exchange splitting of O 2p [1.3 (0.25) eV and 0.36 (0.20) eV for 2pz and 2px, respectively at the zone center (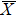 point)].[17] The inverse photoemission spectroscopy clarified that the surface-derived minority-spin Fe 3d3z2−r2 state exists just above EF on clean Fe(001) while the Fe 3d3z2−r2 surface state is quenched and an image-potential state appears on the Fe(001)–p(1 × 1)-O surface.[20] These observations indicate enhanced spin polarization and higher electron reflectivity of the Fe(001)–p(1 × 1)-O surface. The scanning tunneling microscopy and spectroscopy of the Fe(001)–p(1 × 1)-O surface have provided the surface morphology as well as the local density of states (LDOS).[21–24] By comparing the observed LDOS and the theoretical calculations using a Green’s-function multiple-scattering approach within DFT, the peak at −0.7 eV was derived from the hybridization between the Fe 3dxz, 3dyz and O 2px, 2py states in the topmost layer, and the peak just above EF from the hybridization between the Fe 3d3z2 − r2 and O 2pz states in the subsurface layer.[24] Meanwhile, the large spin-dependent electron reflectivity and absorption of the Fe(001)–p(1 × 1)-O surface[25–27] have been successfully applied to the highly efficient target materials for the very low-energy-electron-diffraction (VLEED) type spin detector.[28]
point)].[17] The inverse photoemission spectroscopy clarified that the surface-derived minority-spin Fe 3d3z2−r2 state exists just above EF on clean Fe(001) while the Fe 3d3z2−r2 surface state is quenched and an image-potential state appears on the Fe(001)–p(1 × 1)-O surface.[20] These observations indicate enhanced spin polarization and higher electron reflectivity of the Fe(001)–p(1 × 1)-O surface. The scanning tunneling microscopy and spectroscopy of the Fe(001)–p(1 × 1)-O surface have provided the surface morphology as well as the local density of states (LDOS).[21–24] By comparing the observed LDOS and the theoretical calculations using a Green’s-function multiple-scattering approach within DFT, the peak at −0.7 eV was derived from the hybridization between the Fe 3dxz, 3dyz and O 2px, 2py states in the topmost layer, and the peak just above EF from the hybridization between the Fe 3d3z2 − r2 and O 2pz states in the subsurface layer.[24] Meanwhile, the large spin-dependent electron reflectivity and absorption of the Fe(001)–p(1 × 1)-O surface[25–27] have been successfully applied to the highly efficient target materials for the very low-energy-electron-diffraction (VLEED) type spin detector.[28]
Nevertheless, quantitative investigation of the orbital characters of the energy bands near EF in the surface region is still lacking. In addition, ferromagnetic Fe is a typical multi-band system, and the electron correlation effect depends on the orbital character and momentum direction.[29,30] From this point of view, detailed understanding of electron correlation as well as p–d hybridization of the Fe(001)–p(1 × 1)-O surface is far from satisfactory.
In this study, we have investigated surface- and bulk-derived electronic states near EF of the Fe(001) and Fe(001)–p(1 × 1)-O surfaces by utilizing linear-polarization-dependent high-resolution ARPES measurements combined with state-of-the-art DFT calculations. We have provided experimental evidence for the orbital dependent hybridization between the absorbed O and Fe atoms near EF in the surface region. These observations are further depicted by the layer- and orbital-resolved DFT calculations.
2. Density-functional theory calculationWe have done DFT calculations for a 41 monolayer (ML) thick Fe(001) slab covered with a p(1 × 1) O layer on both surfaces. The DFT calculations were performed using the openMX code,[31] norm-conserving scalar relativistic pseudopotentials, and pseudo-atomic localized basis functions. We used the LSDA functional as proposed by Ceperley and Alder[32] and colinear magnetism. The slab was constructed from a fully relaxed bulk Fe lattice structure and the atomic positions in the slab were subsequently relaxed with residual forces being smaller than 10−4 Bohr/Hartree. The adsorbed oxygen atoms occupied the hollow site of the surface. The Brillouin zone was sampled using a 24 × 24 × 1 k-point mesh and the cut-off energy was 300 Ry. Soft pseudopotentials were used for Fe with a basis set chosen as s3p3d2f1. The O basis was set as s2p2d1.
The slab band dispersion EB(k∥) along the 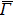 –
–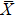 and
and  –
–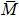 high symmetry lines was then calculated. Since a large number of atoms and hence electrons in the slab are involved in the DFT calculations, the resultant raw band structures are quite complex with many quantum-well-like bands that are related to the electrons contributing to the bulk bands. To discuss the electronic structures at the surface or in the bulk, it is necessary to calculate each contribution from a certain atom in the slab.
high symmetry lines was then calculated. Since a large number of atoms and hence electrons in the slab are involved in the DFT calculations, the resultant raw band structures are quite complex with many quantum-well-like bands that are related to the electrons contributing to the bulk bands. To discuss the electronic structures at the surface or in the bulk, it is necessary to calculate each contribution from a certain atom in the slab.
Using the unfolding procedure implemented in the openMX code,[33,34] we extracted the orbital (l,m) and spin (s) contribution of each atom (A) in the slab layer at each eigenenergy of the electron band dispersion. Then we constructed image plots showing the contributions from each atom as well as orbitals and spins by adding a Gaussian function with an area proportional to the orbital weight IA(l,m,s) to each point of the band dispersion. This method allows us to determine the orbital hybridization as well as the spin structure of the surface and more bulk-like regions deeper inside the slab.
A Mulliken charge analysis[35] was used to analyze the variation of valance of the Fe atoms as a function of position within the slab and to clarify the effect of the charge transfer in the oxygen adsorbed Fe(001) slab. We have found sizable deviation of the charge distribution in the 1st and 2nd Fe layers from that of the central Fe layer (the 21st layer counting from the surface Fe layer, which is regarded as bulk). In the current analysis, therefore, we focus on the electronic structures in the surface region, namely, O atoms at the surface, the 1st and 2nd Fe layers, and the electronic structure of the Fe layer in the bulk (central layer of the slab).
3. ExperimentFe(001) and Fe(001)–p(1 × 1)-O films were grown on MgO(001) substrates. Single-crystalline MgO(001) substrates (one-side polished, 7 mm × 7 mm, 0.5 mm thick) were cleaned by annealing (800 K for 12 h) in an ultrahigh-vacuum chamber (base pressure: 2 × 10−10 Torr). An electron beam evaporator (EFM 3, Omicron, Germany) was used to deposit Fe on MgO(001). The thickness of the Fe film was typically ∼ 100 nm. A well ordered Fe(001) surface was obtained after annealing at 800 K for 30 min. In order to prepare the oxygen adsorbed surface, about 1500 L O2 was dosed on the Fe(001) film (5 × 10−6 Torr for 5 min) at room temperature. Then the sample was heated by flash annealing to 900 K to make a uniform single monolayer of O.
The cleanness of Fe(001) and oxygen adsorbed Fe(001) surfaces was characterized by Auger electron spectroscopy and the 1 × 1 surface structure was confirmed by the LEED image. Figures 1(a) and 1(b) show the LEED images for pure Fe(001) and Fe(001)–p(1 × 1)-O, respectively. A sharp 1 × 1 pattern clearly indicated that our sample surfaces were clean and well-ordered.
High-resolution ARPES experiments were performed on the linear-undulator beamline (BL-1) of a compact electron-storage ring (HiSOR) at Hiroshima University.[36,37] The data were obtained using the angular mode of a hemispherical electron-energy analyzer (R4000, VG-Scienta, Sweden). The analyzer chamber can be rotated around the linearly polarized light axis, which enables us to examine ARPES spectra with the p- or s-polarization geometries. In the p-polarization geometry, the vector potential which is parallel to the electric-field vector lies on the photoelectron detection plane as well as the light incidence plane. On the other hand, in the s-polarization geometry, the vector potential is perpendicular to the detection plane. Within the free-electron final-state approximation, the initial states of even symmetry with respect to the detection plane [= mirror plane of Fe(001)] can be observed using the p-polarization geometry, while those having odd symmetry using the s-polarization geometry.[37]
All of the ARPES results shown in this study were taken at a photon energy of hν = 55 eV for enhanced surface sensitivity. With this photon energy, the bulk bands detected by the ARPES measurements in the normal emission geometry are closer to those at the Γ point of the bulk Brillouin zone.[38] The total energy resolution was set to ΔE = 16 meV. The angular resolution was Δθ = 0.8° (FWHM), which provides a momentum resolution of δk = 0.051 Å−1. The sample temperature was set at 12 K during the ARPES measurements.
4. Orbital symmetry and compatibility relationBy employing a polarization-dependent ARPES experiment, we can selectively observe electronic states having even or odd symmetry with respect to the mirror plane of the sample, and directly compare the results with the DFT calculations. In this analysis, decomposition into the basis functions (xy, yz, zx, x2 − y2, 3z2 − r2, x, y, z) along the high symmetry lines [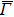 –
–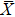 ,
, 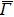 –
–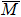 in Fig. 1(c)] is useful.
in Fig. 1(c)] is useful.
Setting the mirror plane standing on the 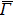 –
– line (y = 0 or ky = 0 plane), the electronic states derived from the Fe 3dxz, 3dx2 − y2, 3d3z2 − r2, and O 2px, 2pz orbitals are even because they do not change their sign under the mirror operation my: y → −y. On the other hand, the electronic states derived from the Fe 3dxy, 3dyz, and O 2py orbitals are odd because they change their sign under the my operation.
line (y = 0 or ky = 0 plane), the electronic states derived from the Fe 3dxz, 3dx2 − y2, 3d3z2 − r2, and O 2px, 2pz orbitals are even because they do not change their sign under the mirror operation my: y → −y. On the other hand, the electronic states derived from the Fe 3dxy, 3dyz, and O 2py orbitals are odd because they change their sign under the my operation.
If we set the mirror plane standing on the 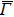 –
– line (x = y or kx = ky plane), the electronic states derived from the Fe 3dxy, 3d(x + y)z, 3d3z2 − r2, and O 2px + y, 2pz are even because they do not change their sign under the mirror operation md: x → y and y → x. On the other hand, the electronic states derived from the Fe 3d(x − y)z, 3dx2 − y2, and O 2px − y orbitals are odd because they change their sign under the md operation. We should note here that in the present calculations the contributions from the Fe 3dxz and 3dyz orbitals are identical to the energy bands along the
line (x = y or kx = ky plane), the electronic states derived from the Fe 3dxy, 3d(x + y)z, 3d3z2 − r2, and O 2px + y, 2pz are even because they do not change their sign under the mirror operation md: x → y and y → x. On the other hand, the electronic states derived from the Fe 3d(x − y)z, 3dx2 − y2, and O 2px − y orbitals are odd because they change their sign under the md operation. We should note here that in the present calculations the contributions from the Fe 3dxz and 3dyz orbitals are identical to the energy bands along the 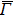 –
–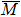 line due to the symmetry property. Namely, the contribution from the Fe 3d(x + y)z orbital is essentially the same with that from the Fe 3dxz and 3dyz orbitals. The situation is the same for O 2px, 2py, and O 2px+ y orbitals. On the other hand, the Fe 3d(x − y)z and O 2px − y contributions are vanishing because the Fe 3dxz and 3dyz (O 2px and 2py) contributions cancel each other along the
line due to the symmetry property. Namely, the contribution from the Fe 3d(x + y)z orbital is essentially the same with that from the Fe 3dxz and 3dyz orbitals. The situation is the same for O 2px, 2py, and O 2px+ y orbitals. On the other hand, the Fe 3d(x − y)z and O 2px − y contributions are vanishing because the Fe 3dxz and 3dyz (O 2px and 2py) contributions cancel each other along the 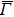 –
– line.
line.
To understand the orbital-dependent p–d hybridization near the surface region, here we consider the compatibility relation for the two-dimensional square lattice.[39] The basis functions are classified into Γ1 (3z2 − r2, z), Γ3 (x2 − y2), Γ4 (xy), and Γ5 (xz, yz, x, y) at the  point.[39] Along the Δ (
point.[39] Along the Δ ( –
–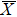 ) line, Γ1, Γ3, and Γ5 are compatible with the Δ1 (+ 1 under the my operation), and Γ4 and Γ5 are compatible with the Δ2 (−1 under the my operation).[39] Along the Σ (
) line, Γ1, Γ3, and Γ5 are compatible with the Δ1 (+ 1 under the my operation), and Γ4 and Γ5 are compatible with the Δ2 (−1 under the my operation).[39] Along the Σ (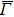 –
– ) line, on the other hand, Γ1, Γ4, and Γ5 are compatible with the Σ1 (+1 under the md operation), and Γ3 and Γ5 are compatible with the Σ2 (−1 under the md operation).[39] The energy bands having the same symmetry can mix with each other if the energy levels are identical along these high symmetry lines. With the p(s)-polarization geometry, we can detect Δ1 (Δ2) and Σ1 (Σ2) along the Δ (Σ) line.
) line, on the other hand, Γ1, Γ4, and Γ5 are compatible with the Σ1 (+1 under the md operation), and Γ3 and Γ5 are compatible with the Σ2 (−1 under the md operation).[39] The energy bands having the same symmetry can mix with each other if the energy levels are identical along these high symmetry lines. With the p(s)-polarization geometry, we can detect Δ1 (Δ2) and Σ1 (Σ2) along the Δ (Σ) line.
In the ARPES experiments, we can also observe the bulk-derived electronic states. Near EF, there exist the minority-spin 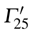 (T2g: xy, yz, zx) and majority-spin Γ12 (Eg: x2 − y2, 3z2 − r2) bands along the Γ–H (Δ) and Γ–N (Σ) lines[40] of the bulk Brillouin zone. Note that taken at hν = 55 eV, the
(T2g: xy, yz, zx) and majority-spin Γ12 (Eg: x2 − y2, 3z2 − r2) bands along the Γ–H (Δ) and Γ–N (Σ) lines[40] of the bulk Brillouin zone. Note that taken at hν = 55 eV, the 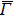 –
– (
(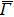 –
–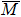 ) line of the surface Brillouin zone is closer to the Γ–H (Γ–N) line of the bulk Brillouin zone.[38]
) line of the surface Brillouin zone is closer to the Γ–H (Γ–N) line of the bulk Brillouin zone.[38]
5. Results and discussionFigures 1(d) and 1(e) show ARPES intensity plots near EF of pure Fe(001) with the p- and s-polarization geometries, respectively. To clearly sort out the energy bands by the orbital symmetry, we have measured ARPES spectra along the  –
– and
and 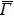 –
– high symmetry lines of the surface Brillouin zone. Since there exists a strong emission-angle dependence in the spectral intensity due to the matrix element effects, we have added the ARPES intensities for the positive and negative directions with respect to the
high symmetry lines of the surface Brillouin zone. Since there exists a strong emission-angle dependence in the spectral intensity due to the matrix element effects, we have added the ARPES intensities for the positive and negative directions with respect to the  point along the high symmetry lines. In Fig. 1(d), an electron-like band dispersion centered at the
point along the high symmetry lines. In Fig. 1(d), an electron-like band dispersion centered at the  point has its energy minimum at −0.2 eV and crossing EF at k∥ = 0.4 Å−1. A broad electron-like band centered at the
point has its energy minimum at −0.2 eV and crossing EF at k∥ = 0.4 Å−1. A broad electron-like band centered at the 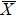 point also crosses EF at k∥ = 0.6 Å−1. Another hole-like band centered at the
point also crosses EF at k∥ = 0.6 Å−1. Another hole-like band centered at the 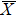 point has its energy maximum near EF. A hole-like band centered at the
point has its energy maximum near EF. A hole-like band centered at the 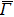 point has energy maximum at −0.2 eV along the
point has energy maximum at −0.2 eV along the 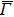 –
– and
and 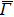 –
–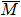 lines. Around the
lines. Around the 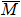 point, a hole-like band is crossing EF at k∥ = 1.18 Å−1 and a broad feature exists around −0.5 eV. Figure 1(e) shows that around the
point, a hole-like band is crossing EF at k∥ = 1.18 Å−1 and a broad feature exists around −0.5 eV. Figure 1(e) shows that around the 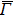 point electron-like bands with energy minimum at −0.2 eV are crossing EF along the
point electron-like bands with energy minimum at −0.2 eV are crossing EF along the  –
– and
and  –
– lines as well as hole-like bands exist just below the energy of −0.2 eV. Moreover, around the
lines as well as hole-like bands exist just below the energy of −0.2 eV. Moreover, around the 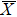 point, a hole-like band crosses EF, which is distinct from the spectral feature in the p-polarization geometry [Fig. 1(d)], suggesting two hole-like Fermi surfaces near the
point, a hole-like band crosses EF, which is distinct from the spectral feature in the p-polarization geometry [Fig. 1(d)], suggesting two hole-like Fermi surfaces near the 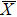 point.
point.
Figures 1(f) and 1(g) show the ARPES intensity plots of Fe(001)–p(1 × 1)-O with the p- and s-polarization geometries, respectively. It is clearly seen that the spectral line widths become narrower after the oxygen adsorption. In Fig. 1(f), along the  –
–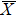 line, electron-like bands Ia and Ib are crossing EF, and another band VI lies between −0.25 eV and EF. Moreover, there exist a hole-like broad band IX having the energy maximum of −0.2 eV at the
line, electron-like bands Ia and Ib are crossing EF, and another band VI lies between −0.25 eV and EF. Moreover, there exist a hole-like broad band IX having the energy maximum of −0.2 eV at the  point and a hole-like band XI centered at the
point and a hole-like band XI centered at the  point. Along the
point. Along the  –
–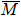 line, on the other hand, electron-like bands II and III are crossing EF around k∥ = 0.3–0.4 Å−1. A hole-like band X exists below bands II and III with the energy maximum at −0.2 eV at the
line, on the other hand, electron-like bands II and III are crossing EF around k∥ = 0.3–0.4 Å−1. A hole-like band X exists below bands II and III with the energy maximum at −0.2 eV at the 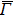 point. A hole-like band VIII is crossing EF at k∥ = 1.23 Å−1, which is similar to the pure Fe in Fig. 1(d). The energy band VII newly appears between band III and band VIII, and a hole-like band XII with a flat portion at about −0.45 eV around the
point. A hole-like band VIII is crossing EF at k∥ = 1.23 Å−1, which is similar to the pure Fe in Fig. 1(d). The energy band VII newly appears between band III and band VIII, and a hole-like band XII with a flat portion at about −0.45 eV around the 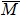 point. In Fig. 1(g), along the
point. In Fig. 1(g), along the 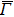 –
–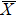 line, electron-like bands VIa and VIb are crossing EF, and a hole-like band XIII exists with the energy maximum at −0.2 eV at the
line, electron-like bands VIa and VIb are crossing EF, and a hole-like band XIII exists with the energy maximum at −0.2 eV at the 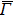 point. Moreover, there exists a hole-like broad band XV having the energy maximum of −0.4 eV at the
point. Moreover, there exists a hole-like broad band XV having the energy maximum of −0.4 eV at the 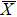 point. A broad feature XVI approaching to EF around the
point. A broad feature XVI approaching to EF around the 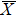 point is also discernible. Along the
point is also discernible. Along the  –
– line, an electron-like band V is crossing EF and a hole-like band XIV exists at the
line, an electron-like band V is crossing EF and a hole-like band XIV exists at the 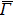 point.
point.
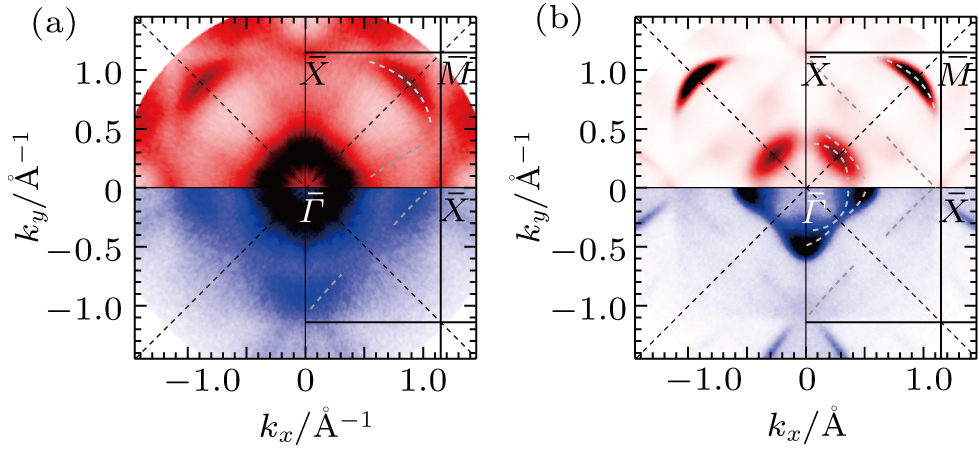
Figures 2(a) and 2(b) show the observed Fermi surfaces of pure Fe(001) and Fe(001)–p(1 × 1)-O, respectively, taken within the p (upper panel) and s (lower panel) polarization geometries. In Fig. 2(a), a rounded-square-like Fermi surface exists around the  point in both p- and s-polarization geometries. In the upper half, one can clearly see an arc-like Fermi surface near the
point in both p- and s-polarization geometries. In the upper half, one can clearly see an arc-like Fermi surface near the 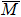 point, and there also exist weak features in between the
point, and there also exist weak features in between the  –
–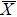 and
and  –
–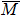 lines. In the lower half, on the other hand, a square-like Fermi surface having a corner at the
lines. In the lower half, on the other hand, a square-like Fermi surface having a corner at the 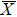 point can be seen. After oxygen adsorption, in Fig. 2(b), as the linewidth is significantly narrowed, the shape of the Fermi surfaces can be clearly identified. One can see square-like Fermi surfaces surrounding the
point can be seen. After oxygen adsorption, in Fig. 2(b), as the linewidth is significantly narrowed, the shape of the Fermi surfaces can be clearly identified. One can see square-like Fermi surfaces surrounding the 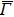 point, an arc-shaped Fermi surface near the
point, an arc-shaped Fermi surface near the  point, and square-like Fermi surfaces having a corner at the
point, and square-like Fermi surfaces having a corner at the 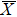 point.
point.
As demonstrated in Figs. 1 and 2, significant modifications of the electronic states occur near EF after the oxygen adsorption. To analyze the p–d hybridization in more detail, we will compare the results with the layer- and orbital-resolved DFT calculations.
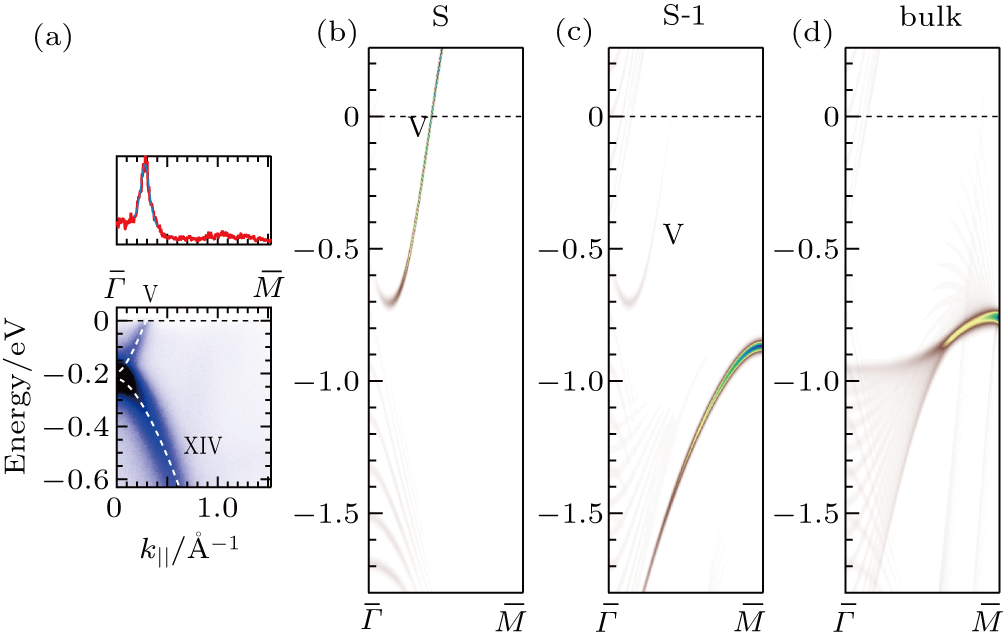
Figure 3(a) shows the ARPES intensity plot and a momentum distribution curve (MDC) at EF taken with the p-polarization geometry. The MDC is the photoemission intensity distribution as a function of k∥ at fixed energy. Based on the lineshape analysis of the MDC at EF, we have evaluated Fermi wave number (kF) values of the bands. In Fig. 3(a), the electron-like bands Ia and Ib cross EF at k∥ = 0.36 Å−1 and k∥ = 0.28 Å−1, respectively. The hole-like band XI crosses EF near the 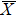 point.
point.
Figures 3(b)–3(d) show the layer-resolved DFT results for the topmost layer (S), the second layer (S-1), and the layer in the bulk (the central layer of the 41 ML slab). In Figs. 3(b) and 3(c), there exists a surface-derived electron-like state with kF = 0.75 Å−1, corresponding to the bands Ia and Ib in Fig. 3(a). However, the theoretical kF value is more than two times larger than the observed ones, and there is no splitting as seen in the ARPES results. Furthermore, the observed energy for the bottom of the bands Ia and Ib is about −0.2 eV at the  point while it is about −0.7 eV in the DFT calculation. Taking into account the effective mass enhancement by a factor of 2–3 due to electron correlation for pure Fe,[29,30] one may consider that the observed bands Ia and Ib are elevated towards EF in the same way. In the present case, however, this explanation is not sufficient as the kF values clearly differ between experiment and theory. This indicates the change of the Fermi surface volume, namely, change of the carrier density in addition to possible band renormalization effect, which is one of the characteristics of the multi-band electron systems.[41]
point while it is about −0.7 eV in the DFT calculation. Taking into account the effective mass enhancement by a factor of 2–3 due to electron correlation for pure Fe,[29,30] one may consider that the observed bands Ia and Ib are elevated towards EF in the same way. In the present case, however, this explanation is not sufficient as the kF values clearly differ between experiment and theory. This indicates the change of the Fermi surface volume, namely, change of the carrier density in addition to possible band renormalization effect, which is one of the characteristics of the multi-band electron systems.[41]
To clarify the electronic states in more detail, we compare the ARPES results with the layer- and orbital-resolved DFT calculations relevant for the p-polarization geometry along the 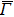 –
– line [Figs. 4(a)–4(k)]. One can see that an electron-like band having orbital character of dxz [Figs. 4(a) and 4(b)] and dx2 − y2 [Figs. 4(d) and 4(e)] crosses EF along the
line [Figs. 4(a)–4(k)]. One can see that an electron-like band having orbital character of dxz [Figs. 4(a) and 4(b)] and dx2 − y2 [Figs. 4(d) and 4(e)] crosses EF along the 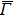 –
–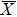 line, which corresponds to the observed bands Ia and Ib. However, in the DFT calculations, the dxz and dx2 − y2 energies are degenerated along the
line, which corresponds to the observed bands Ia and Ib. However, in the DFT calculations, the dxz and dx2 − y2 energies are degenerated along the 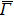 –
–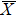 line. Note that the dxz contributions from the S and S-1 layers are large near the
line. Note that the dxz contributions from the S and S-1 layers are large near the  point while the dx2 − y2 contribution from the S layer is large near EF. There are corresponding features in O px [near the
point while the dx2 − y2 contribution from the S layer is large near EF. There are corresponding features in O px [near the 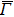 point in Fig. 4(j)], pz [near EF in Fig. 4(k)], indicating the existence of the p–d hybridization in the surface region. Later, by combining with the results from the s-polarization geometry, we will identify the orbital characters of the split energy bands observed in the ARPES.
point in Fig. 4(j)], pz [near EF in Fig. 4(k)], indicating the existence of the p–d hybridization in the surface region. Later, by combining with the results from the s-polarization geometry, we will identify the orbital characters of the split energy bands observed in the ARPES.
The observed band XI corresponds to the dx2 − y2 orbital in the S-1 and bulk layers [Figs. 4(e) and 4(f)] as well as the d3z2 − r2 orbital in the S, S-1 and bulk layers [Figs. 4(g), 4(h) and 4(i)]. The corresponding features in O px, pz [near the  point in Figs. 4(j) and 4(k)] indicate the existence of the p–d hybridization in the surface region. The band VI in Fig. 3(a) corresponds to the dxz orbital [Fig. 4(c)] in the bulk and the band IX corresponds to the d3z2 − r2 orbital [Fig. 4(i)] in the bulk, which is consistent with the absence of the corresponding feature in the oxygen derived states in Figs. 4(j) and 4(k).
point in Figs. 4(j) and 4(k)] indicate the existence of the p–d hybridization in the surface region. The band VI in Fig. 3(a) corresponds to the dxz orbital [Fig. 4(c)] in the bulk and the band IX corresponds to the d3z2 − r2 orbital [Fig. 4(i)] in the bulk, which is consistent with the absence of the corresponding feature in the oxygen derived states in Figs. 4(j) and 4(k).
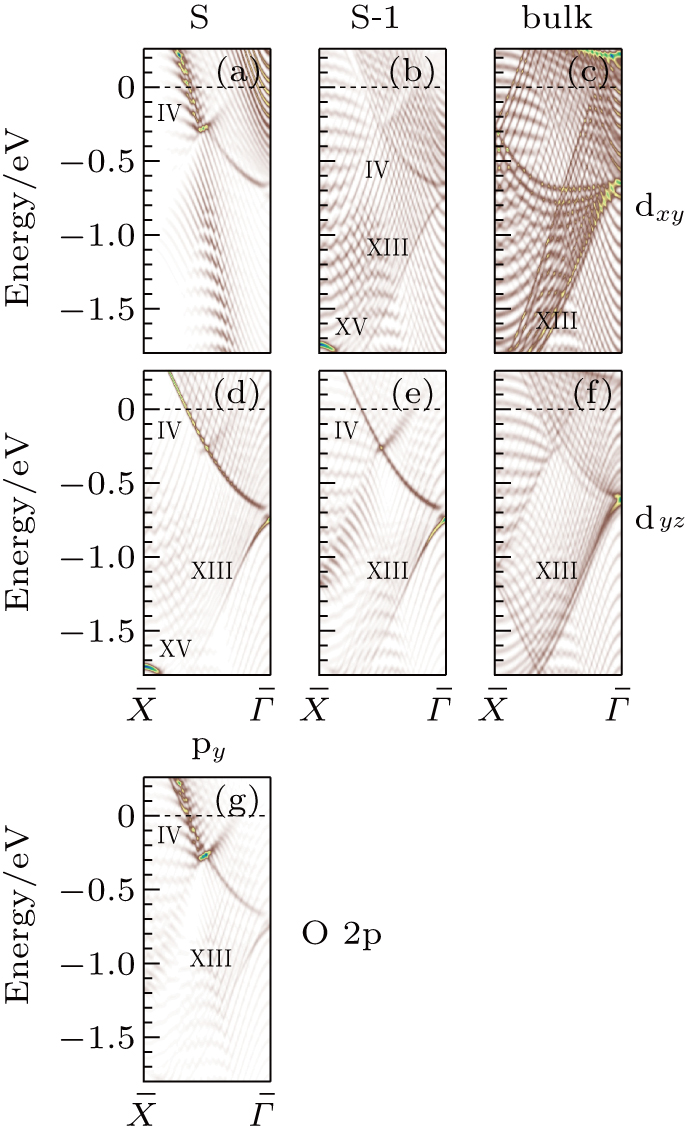
Figure 5(a) shows the ARPES intensity plot and the MDC at EF taken with the s-polarization geometry along the 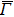 –
–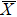 line. Based on the analysis of the MDC, the bands IVa and IVb cross EF at k∥ = 0.50 Å−1 and k∥ = 0.34 Å−1, respectively. In Figs. 5(b) and 5(c), the layer-resolved DFT results also show electron-like and hole-like bands centered at the
line. Based on the analysis of the MDC, the bands IVa and IVb cross EF at k∥ = 0.50 Å−1 and k∥ = 0.34 Å−1, respectively. In Figs. 5(b) and 5(c), the layer-resolved DFT results also show electron-like and hole-like bands centered at the  point corresponding to the bands IVa/IVb and XIII. The layer- and orbital-resolved DFT results in Figs. 6(a)–6(f) further reveal that these states are derived from the dxy and dyz orbitals mainly from the S and S-1 layers. The O py orbital in Fig. 6(g) also shows features corresponding to the bands IVa/IVb and XIII, showing the p–d hybridization near the surface layers. On the other hand, the band XV is derived from the dyz in the S layer [Fig. 6(d)] and dxy in the S-1 layer [Fig. 6(b)] with the negligible py contribution. Note that the observed band energy −0.40 eV at the
point corresponding to the bands IVa/IVb and XIII. The layer- and orbital-resolved DFT results in Figs. 6(a)–6(f) further reveal that these states are derived from the dxy and dyz orbitals mainly from the S and S-1 layers. The O py orbital in Fig. 6(g) also shows features corresponding to the bands IVa/IVb and XIII, showing the p–d hybridization near the surface layers. On the other hand, the band XV is derived from the dyz in the S layer [Fig. 6(d)] and dxy in the S-1 layer [Fig. 6(b)] with the negligible py contribution. Note that the observed band energy −0.40 eV at the 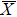 point is much elevated compared with the DFT result −1.73 eV, which corresponds to an effective mass enhancement factor of ∼ 4.
point is much elevated compared with the DFT result −1.73 eV, which corresponds to an effective mass enhancement factor of ∼ 4.
Here we consider the origin of the split electron-like bands as observed in the ARPES results along the 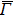 –
– line taking into account the symmetry properties of the orbitals. We assume the dxz- and dyz-orbital contributions, as observed in the p- and s-polarization geometries, respectively, should be similar near the
line taking into account the symmetry properties of the orbitals. We assume the dxz- and dyz-orbital contributions, as observed in the p- and s-polarization geometries, respectively, should be similar near the 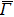 point because they are classified as the Γ5 of a square lattice at the
point because they are classified as the Γ5 of a square lattice at the 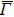 point. In this case, we can assign the bands Ia and IVb having similar kF values, 0.34–0.36 Å−1, near the
point. In this case, we can assign the bands Ia and IVb having similar kF values, 0.34–0.36 Å−1, near the  point as derived from the dxz and dyz orbitals, respectively. Then the band Ib at 0.28 Å−1 is likely to be derived from the dx2 − y2 (Γ3) orbital, and the band IVa at 0.50 Å−1 from the dxy (Γ4) orbital.
point as derived from the dxz and dyz orbitals, respectively. Then the band Ib at 0.28 Å−1 is likely to be derived from the dx2 − y2 (Γ3) orbital, and the band IVa at 0.50 Å−1 from the dxy (Γ4) orbital.
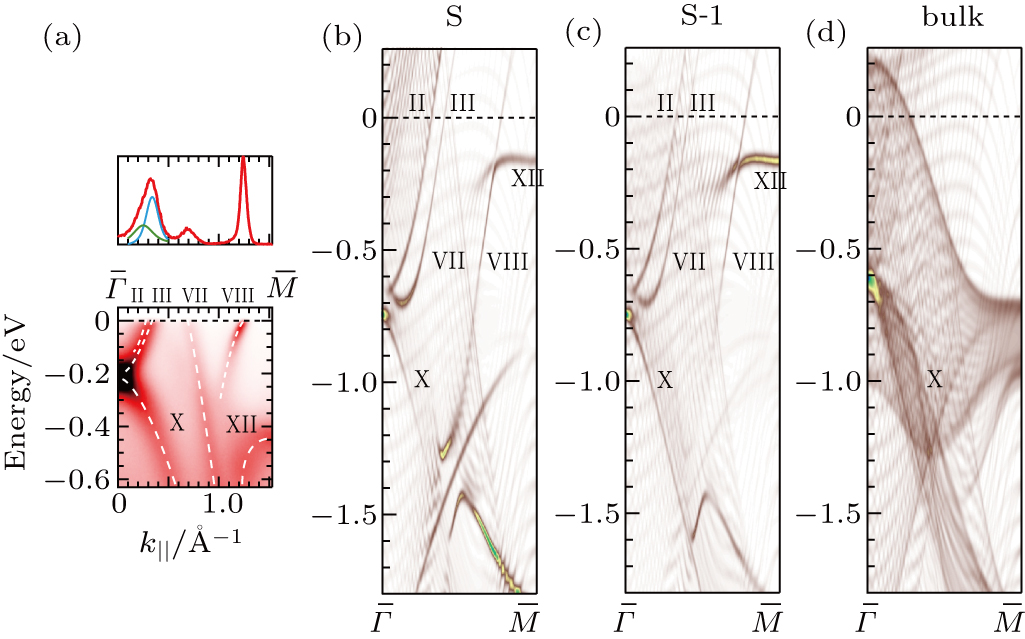
Figure 7(a) shows the ARPES intensity plot and MDC at EF with the p-polarization geometry along the 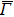 –
–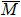 line. Analyses of the MDC at EF indicate the existence of two electron-like bands II and III crossing EF at k∥ = 0.25 Å−1 and k∥ = 0.34 Å−1, respectively. In Figs. 7(b) and 7(c), the DFT calculations indicate the surface-derived bands corresponding to the bands II and III. In the calculations, these bands cross EF at k∥ = 0.49 Å−1 and k∥ = 0.62 Å−1, which are larger than the observed kF values though the deviations are slightly smaller than those along the
line. Analyses of the MDC at EF indicate the existence of two electron-like bands II and III crossing EF at k∥ = 0.25 Å−1 and k∥ = 0.34 Å−1, respectively. In Figs. 7(b) and 7(c), the DFT calculations indicate the surface-derived bands corresponding to the bands II and III. In the calculations, these bands cross EF at k∥ = 0.49 Å−1 and k∥ = 0.62 Å−1, which are larger than the observed kF values though the deviations are slightly smaller than those along the  –
–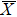 line (see
line (see  values along
values along  –
– and
and 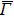 –
– lines in Table 1). On the other hand, the Fermi wave number for the band VIII (1.23 Å−1) is slightly larger than the calculation (1.18 Å−1) and that for VII (0.68 Å−1) is close to the theoretical one (0.69 Å−1). These observations suggest that the Fermi surfaces are deformed inhomogeneously depending on the orbital character as well as momentum direction.
lines in Table 1). On the other hand, the Fermi wave number for the band VIII (1.23 Å−1) is slightly larger than the calculation (1.18 Å−1) and that for VII (0.68 Å−1) is close to the theoretical one (0.69 Å−1). These observations suggest that the Fermi surfaces are deformed inhomogeneously depending on the orbital character as well as momentum direction.
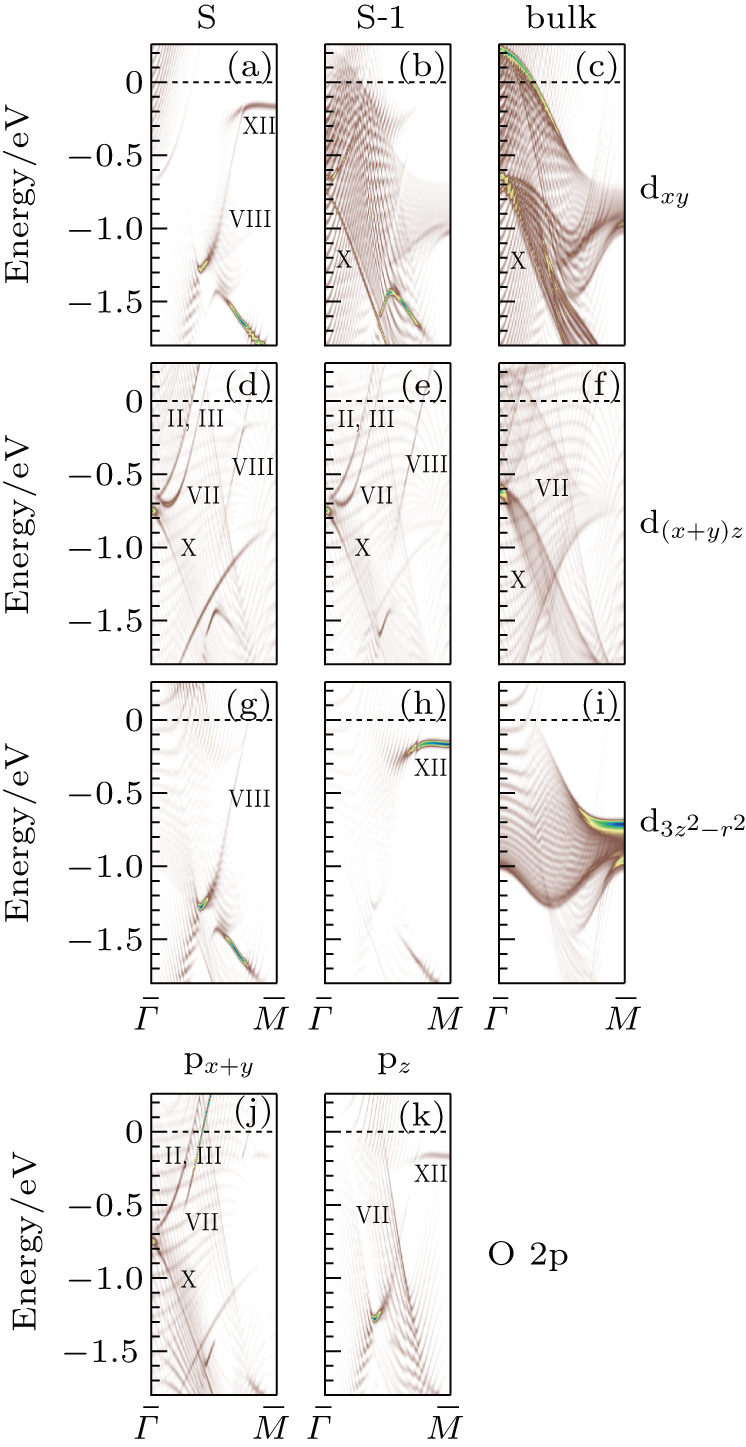
In Figs. 8(d) and 8(e), the layer- and orbital-resolved DFT results indicate that the bands II and III are mainly derived from the d(x+ y)z orbital on the S and S-1 layers. The hole-like band X at the 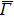 point is either from dxy or d(x + y)z [Figs. 8(b), 8(c), and 8(d)–8(f)]. The corresponding feature exists in the O px+ y orbital [near the
point is either from dxy or d(x + y)z [Figs. 8(b), 8(c), and 8(d)–8(f)]. The corresponding feature exists in the O px+ y orbital [near the  point in Fig. 8(j)], indicating the p–d hybridization. On the other hand, band VII is derived from the d(x + y)z orbital [Figs. 8(d)–8(f)] and the px + y, pz orbitals [Figs. 8(j) and 8(k)]. In the case of band VIII, it corresponds to the dxy and d3z2 − r2 orbitals in the S layer [Figs. 8(a) and 8(g)], and to the d(x + y)z orbital in the S and S-1 layers [Figs. 8(d) and 8(e)]. The corresponding features in the O px + y and pz orbitals are weak.
point in Fig. 8(j)], indicating the p–d hybridization. On the other hand, band VII is derived from the d(x + y)z orbital [Figs. 8(d)–8(f)] and the px + y, pz orbitals [Figs. 8(j) and 8(k)]. In the case of band VIII, it corresponds to the dxy and d3z2 − r2 orbitals in the S layer [Figs. 8(a) and 8(g)], and to the d(x + y)z orbital in the S and S-1 layers [Figs. 8(d) and 8(e)]. The corresponding features in the O px + y and pz orbitals are weak.
The hole-like band XII at the  point is mainly derived from the d3z2 − r2 orbital of the S-1 layer [Fig. 8(h)], with a minor contribution from the dxy orbital of the S layer [Fig. 8(a)]. There is a clear corresponding feature in O pz orbital [Fig. 8(k)], indicating the existence of the p–d hybridization around the
point is mainly derived from the d3z2 − r2 orbital of the S-1 layer [Fig. 8(h)], with a minor contribution from the dxy orbital of the S layer [Fig. 8(a)]. There is a clear corresponding feature in O pz orbital [Fig. 8(k)], indicating the existence of the p–d hybridization around the  point. We should note that the band XII is located at −0.45 eV at the
point. We should note that the band XII is located at −0.45 eV at the 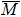 point which is much lower than the theoretical value −0.2 eV, showing a significant contrast to the bands II and III around the
point which is much lower than the theoretical value −0.2 eV, showing a significant contrast to the bands II and III around the  point having higher energies compared with the DFT results. This observation seems to support our assignment of the band IVa as the dxy orbital in the S layer which has larger kF value compared with the dxz, dyz, and dx2 − y2 orbitals. These results also indicate the interplay of the p–d hybridization and electron correlation depending on the orbital characters.[41]
point having higher energies compared with the DFT results. This observation seems to support our assignment of the band IVa as the dxy orbital in the S layer which has larger kF value compared with the dxz, dyz, and dx2 − y2 orbitals. These results also indicate the interplay of the p–d hybridization and electron correlation depending on the orbital characters.[41]
Figure 9(a) shows the ARPES intensity plot and the MDC at EF with the s-polarization geometry along the 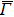 –
– line. Based on the MDC analysis, the band V has the kF value of 0.28 Å−1. As shown in Figs. 9(b) and 9(c), the band V is derived from the dx2 − y2 orbital. The contribution from the S layer is significant compared with that from the S-1 layer. As for the band XIV, however, we could not clearly identify corresponding features in the DFT results. Note that the kF values for the dx2 − y2 orbital are identical along the
line. Based on the MDC analysis, the band V has the kF value of 0.28 Å−1. As shown in Figs. 9(b) and 9(c), the band V is derived from the dx2 − y2 orbital. The contribution from the S layer is significant compared with that from the S-1 layer. As for the band XIV, however, we could not clearly identify corresponding features in the DFT results. Note that the kF values for the dx2 − y2 orbital are identical along the 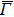 –
– and
and  –
–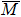 lines. While the DFT calculations show a hole-like structure centered at the
lines. While the DFT calculations show a hole-like structure centered at the  point in Figs. 9(c) and 9(d), we could not observe the corresponding spectral feature in the ARPES results in the energy range between −0.6 eV and EF.
point in Figs. 9(c) and 9(d), we could not observe the corresponding spectral feature in the ARPES results in the energy range between −0.6 eV and EF.
In Table 1, we summarize the assignment of the orbital character of the observed bands obtained from the detailed comparison between the ARPES results (energy range:−0.6 eV to EF) and layer- and orbital-resolved DFT calculations. We find the significant p–d hybridization between the Fe dxz, dyz, dxy, dx2 − y2 and O px, py orbitals in the topmost layer, and the d3z2 − r2 and pz orbitals in the S-1 layer. These observations are consistent with the symmetry properties of the two-dimensional square lattice[39] as well as previous DFT results.[11] We also find that the bands VI, IX, XV along the  –
–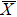 line, and VIII, V along the
line, and VIII, V along the 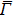 –
– line are weakly hybridized with the adsorbed oxygen.
line are weakly hybridized with the adsorbed oxygen.
Table 1.
Table 1.
 Table 1. Orbital character of the observed bands. S, S-1, B denote the topmost, second, and bulk Fe layers, respectively. 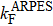 and and 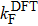 in units of Å−1 represent the Fermi wave number obtained from the ARPES and DFT results, respectively. in units of Å−1 represent the Fermi wave number obtained from the ARPES and DFT results, respectively. .
| Direction |
Polarization |
Band |
Fe orbital (layer) |
O orbital |
 |
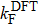 |
 |
 – – |
p |
Ia |
dxz (S, S-1) |
px, pz |
0.36 |
0.75 |
0.48 |
|
p |
Ib |
dx2 − y2 (S, S-1) |
px, pz |
0.28 |
0.75 |
0.37 |
|
p |
VI |
dxz (B) |
– |
|
|
|
|
p |
IX |
d3z2 − r2 (B) |
– |
|
|
|
|
p |
XI |
dx2 − y2 (S-1,B), d3z2 − r2 (S,S-1,B) |
px, pz |
|
|
|
|
s |
IVa |
dxy (S, S-1) |
py |
0.50 |
0.74 |
0.68 |
|
s |
IVb |
dyz (S, S-1) |
py |
0.34 |
0.74 |
0.46 |
|
s |
XIII |
dyz (S,S-1,B), dxy (S-1,B) |
py |
|
|
|
|
s |
XV |
dyz (S), dxy (S-1) |
– |
|
|
|
|
s |
XVI |
dxy (S)? |
– |
|
|
|
 – – |
p |
II, III |
d(x + y)z (S, S-1) |
px + y |
0.25, 0.34 |
0.49, 0.62 |
0.51, 0.55 |
|
p |
VII |
dx + y)z (S, S-1, B) |
px + y, pz |
0.68 |
0.69 |
0.99 |
|
p |
VIII |
d3z2 − r2 (S), dxy (S), d(x + y)z (S, S-1) |
– |
1.23 |
1.18 |
1.04 |
|
p |
X |
d(x + y)z (S, S-1, B), dxy (S-1, B) |
px + y |
|
|
|
|
p |
XII |
dxy (S), d3z2 − r2 (S-1) |
pz |
|
|
|
|
|
s |
V |
d}x2 − y2 (S,S-1) |
– |
0.28 |
0.62 |
0.45 |
|
s |
XIV |
dx2 − y2 (S,S-1,B)? |
– |
|
|
|
| Table 1. Orbital character of the observed bands. S, S-1, B denote the topmost, second, and bulk Fe layers, respectively. 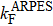 and and 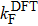 in units of Å−1 represent the Fermi wave number obtained from the ARPES and DFT results, respectively. in units of Å−1 represent the Fermi wave number obtained from the ARPES and DFT results, respectively. . |
Finally it should be emphasized that the electron-like bands I–V near the 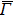 point are shifted to a higher energy compared with the DFT calculations, while the energy of band XII is shifted downwards. The theoretical kF values for the electron-like Fermi surfaces around the
point are shifted to a higher energy compared with the DFT calculations, while the energy of band XII is shifted downwards. The theoretical kF values for the electron-like Fermi surfaces around the 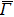 point are larger than the observed kF values, and the magnitudes of the deviation depend on the orbital character and momentum direction. These observations indicate the significance of the anisotropic interplay of electron correlation and p–d hybridization in the multi-band low-dimensional electron system.
point are larger than the observed kF values, and the magnitudes of the deviation depend on the orbital character and momentum direction. These observations indicate the significance of the anisotropic interplay of electron correlation and p–d hybridization in the multi-band low-dimensional electron system.
6. ConclusionWe have studied the electronic states of clean Fe(001) and Fe(001)–p(1 × 1)-O films grown on MgO(001) substrates near EF in the surface region by means of polarization-dependent ARPES measurements and extensive DFT calculations. We have observed significant modifications of the energy bands and the Fermi surfaces induced by the oxygen adsorption. Based on the detailed comparison between the ARPES results and DFT calculations, we have found the orbital-dependent p–d hybridization in the topmost and second Fe layers. We have also found that the observed band energy and kF values are deviated from the DFT calculations depending on the orbital characters and momentum directions. It clearly indicates the anisotropic interplay of the electron correlation and p–d hybridization effects near the surface region. Our results have provided a comprehensive view of the electronic states near EF of the oxygen adsorbed Fe(001) surface as well as insight into electron correlation in the multi-band low-dimensional electron system.