† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11674187 and 51871127) and Technology on Electronic Test & Measurement Laboratory (Grant No. 6142001180103).
Nowadays the yttrium iron garnet (Y3Fe5O12, YIG) films are widely used in the microwave and spin wave devices due to their low damping constant and long propagation distance for spin waves. However, the performances, especially the frequency stability, are seriously affected by the relaxation of the interface magnetic moments. In this study, the effect of out-of-plane magnetization depinning on the resonance frequency shift (Δfr) was investigated for 3-μm YIG films grown on Gd3Ga5O12 (GGG) (111) substrates by liquid-phase epitaxy. It is revealed that the ferromagnetic resonance (FMR) and spin wave propagation exhibit a very slow relaxation with relaxation time τ even longer than one hour under an out-of-plane external magnetic bias field. The Δfr span of 15.15–24.70 MHz is observed in out-of-plane FMR and forward volume spin waves. Moreover, the Δfr and τ depend on the magnetic field. The Δfr can be attributed to that the magnetic moments break away from the pinning layer at the YIG/GGG interface. The thickness of the pinning layer is estimated to be about 9.48 nm to 15.46 nm according to the frequency shifting. These results indicate that Δfr caused by the pinning layer should be addressed in the design of microwave and spin wave devices, especially in the transverse magnetic components.
Spin magnetic moments of the electrons in magnetic materials will be precessing around their equilibrium position in an external field with a ferromagnetic resonance (FMR) frequency. If the spin precessions are not uniform, the propagation of collective precessions in a ferromagnet forms spin waves (the magnons are the quanta of spin waves).[1,2] The conventional complementary metal–oxide–semiconductor (CMOS) based electronics can no longer meet the requirements of high processing speed, small size, and low power consumption, one of the alternative methods having the ability to satisfy the above requirements is magnonics.[3–10] The aim of magnonics is to use spin waves to transmit, store, and process the information.[11–17] By encoding the information into the electron spin-angular momentum instead of the electron charge, the data can be processed faster with lower-energy dissipation.[18–23] In out-of-plane magnetized ferromagnetic films, the excited spin waves are called forward volume spin waves (FVMSW), here the group velocity vg and the wave vector k are parallel. Unlike the backward volume magnetostatic waves (BVMSW) and magnetostatic surface spin waves (MSSW) excited in an in-plane magnetized ferromagnetic film, the FVMSW is isotropic, thus, overcomes the limitations of anisotropy spin waves in in-plane magnetized ferromagnetic films.[24]
For practical devices, it is essential that spin waves have a long propagation distance. Yttrium iron garnet (Y3Fe5O12, YIG) is a proverbial ferromagnetic insulator with uniquely low magnetic damping, and spin waves can propagate a long distance over several centimeters in it, so it is the best material for magnonic devices so far.[11,25] In recent years, high-quality YIG films with ultralow damping for magnonic devices have been grown on gadolinium gallium garnet (Gd3Ga5O12, GGG) substrates by liquid phase epitaxy,[26] radio frequency magnetron sputtering,[27] or pulsed laser deposition.[28] After the preparation of high-quality YIG thin films, the FMR and spin wave propagation properties of the films have been extensively studied.[15,29] In addition, spin-related phenomena such as spin pumping effect,[30] spin Hall magnetoresistance,[31] and spin Seebeck effect[32–34] in YIG films have aroused great interest in research. Meanwhile, YIG-based magnonic devices such as phase shifters, logic gates, filters, and multiplexers have been investigated. Propagation of short-wavelength spin waves in YIG films and interfacial spin-torque excited exchange spin waves have also been studied.[23,35] Among all the researches above, the frequency stability of FMR and spin waves in YIG films under a constant external magnetic bias field is very important either in fundamental research or the device design. However, there are rare reports about the frequency stability due to the inhomogeneous magnetization of YIG films. In this study, for the first time, the serious influence of magnetization relaxation in the pinning layer on the out-of-plane magnetized FMR frequency fr, the FVMSW frequency fFVMSW, and relaxation time τ was investigated. The results show that the fr and fFVMSW reduce with time. The frequency shift Δf can be attributed to that the magnetic moments at the YIG/GGG interface break away from the pinning layer. This study will provide valuable guidance for the application of YIG in FMR and spin wave devices.
The 3-μm YIG films were grown on single-crystal GGG (111) substrates using liquid phase epitaxy. Two YIG films of different dimensions were used to measure FMR and spin waves, respectively. Sample 1 with dimension of 2.5 mm× 2.5 mm was used to measure FMR. Sample 2, a long strip waveguide with dimension of 10 mm× 0.8 mm, was used to measure the propagation of the spin waves. The edges of the waveguide were cut to a 45° angle to avoid the influence of reflected spin waves. The crystal structure of the YIG films was characterized by high-resolution x-ray diffraction (XRD). As shown in Fig.
 | Fig. 1. (a) XRD θ–2θ scan of the (444) reflections from a YIG film grown on a GGG (111) substrate. Room-temperature in-plane (b) and out-of-plane (c) hysteresis loops of the YIG film. |
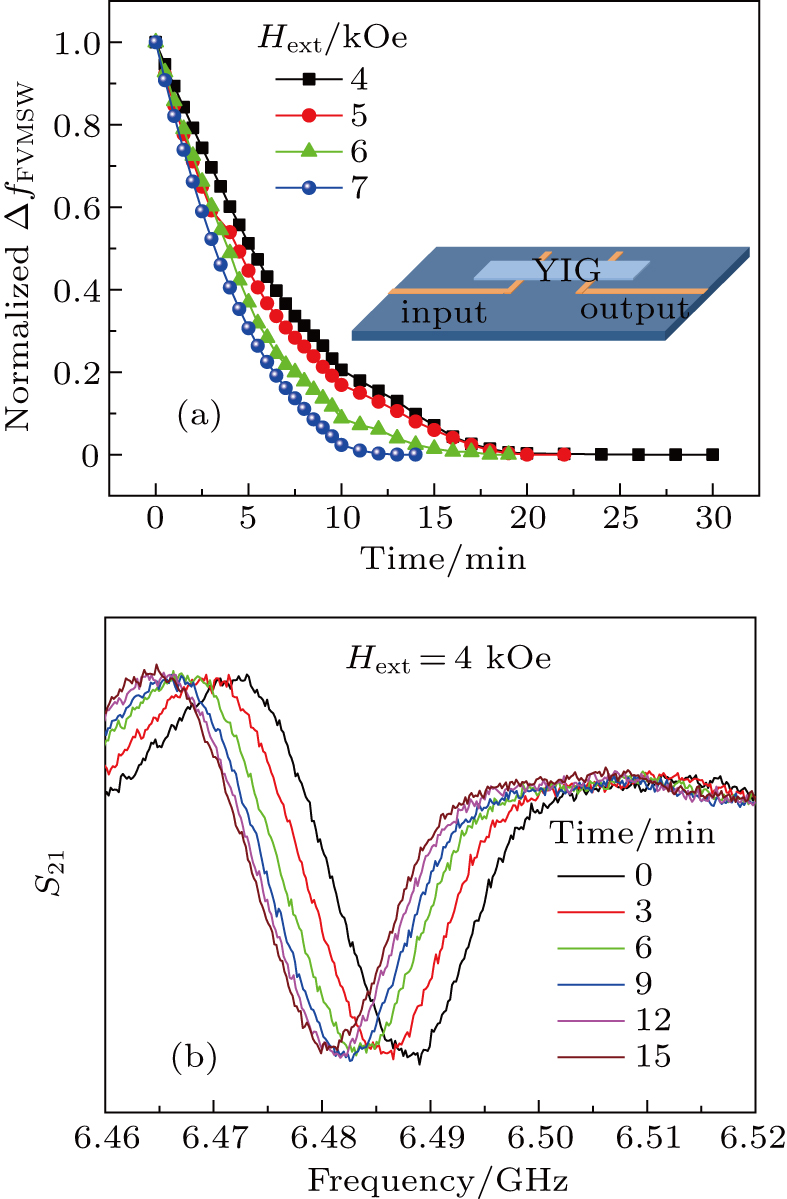
In the practical experiment, the magnetic moments will take a very long time (about 24 hours) to completely recover to the random dispersion state. However, in order to ensure the data reliability, the magnetic relaxation process should be measured in the same sample, whose initial state should have a random dispersion of magnetic moments. For doing so, an ultrasonic vibration method was adopted to drive the moments to quickly recover to the random dispersion state after a measurement under a large magnetic field. The effect of the ultrasonic time on the moment recover process was explored. It is revealed that an ultrasonic vibration of half an hour is sufficient to bring the YIG moments to random dispersion. Therefore, treating the sample by ultrasonic vibration for 30 min after a measurement was adopted in this study. In addition, in order to ensure a stable magnetic field, in this experiment, a high stable power supply was adopted with a magnetic field stability better than 1 mOe/h.
A vector network analyzer (VNA, Agilent N5224 A) was employed to measure FMR spectra and spin wave transmission spectra using scattering parameter S21. Two different measurement configurations were used to measure VNA-FMR and spin wave propagation, respectively. The FMR measurements were performed using a coplanar waveguide (CPW) with a signal line width of 300 μm and a distance of 220 μm between the signal line and the ground plane. The CPW was connected to the VNA ports, and the FMR spectra were measured by recording the S21 parameter as a function of frequency f and external magnetic field Hext. Spin wave transmission spectra were measured by a YIG waveguide with input and output microwave microstrip antennas. The microwave signal through the input antenna generates an alternating magnetic field. The vertical component of the field perpendicular to the mean spins precession axis creates a torque that increases the precessional amplitude above the thermal level. Spins precessing under the antenna interact with the surrounding spins via exchange interaction, and when the field and frequency satisfy the appropriate conditions, the spin waves are propagating in the film. When the spin waves arrive at the output antenna, a microwave signal is induced through the inverse of the excitation process, and is detected by the VNA. By measuring S21 or S12 parameter, the spin wave transmission spectra in the sample can be obtained. The variation of fr and fFVMSW with time was obtained by recording the S21 parameter in a time interval under a fixed external magnetic field.
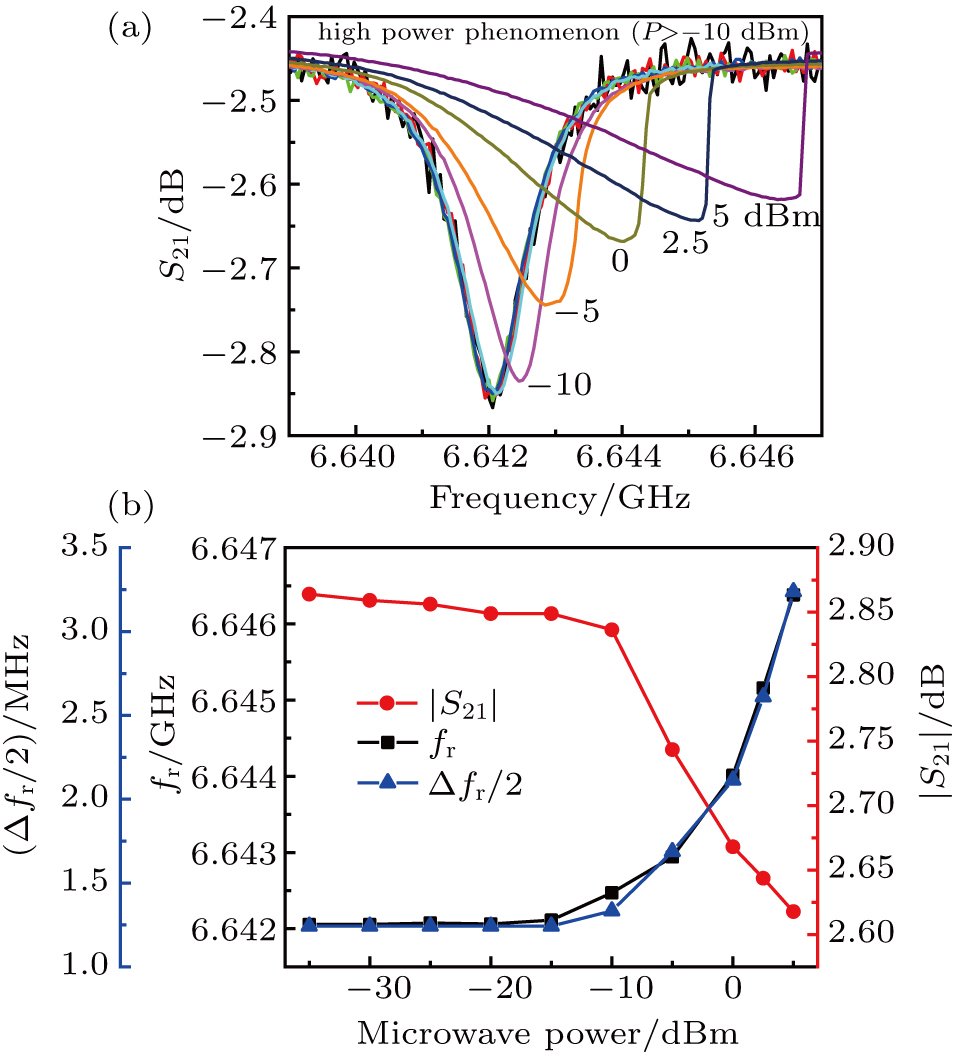
In order to eliminate the influence of the microwave power on the FMR frequency and determine the optimum experimental condition, the S21 parameter was measured as a function of frequency f and microwave power P under a fixed out-of-plane external magnetic field Hext of 4.03 kOe. Figure
As described above, ultrasonic vibration was carried out for half an hour before the FMR measurement to eliminate the residual orientation of magnetic moments by the previous magnetization, and to return the sample to the state of random distribution of magnetic moments. The FMR measurement should be carried out immediately when Hext reaches to the set value of the measuring field. Figure
 | Fig. 3. (a) Time dependence of out-of-plane FMR frequency shift Δfr under various applied external magnetic fields Hext, (b) the normalized Δfr–time curves. |
The relationship between FMR frequency fr and out-of-plane external magnetic field Hext can be written approximately as

In order to estimate the thickness of the pinning layer, the accurate gyromagnetic ratio γ/2π and saturation magnetization 4πMS of the YIG thin film were measured. The FMR spectra under various normal magnetic fields were recorded, and then the fr–Hext curve was fitted using Eq. (

The properties of spin waves depend on the strength of the dipolar and exchange interactions in the materials. As the wavelength of the spin wave becomes shorter, the angle between neighboring spins increases, and the energy of their exchange interaction increases too. Therefore, the long wavelength spin waves are dipole-dominated spin waves and the short wavelength spin waves are exchange-dominated spin waves. Generally speaking, the exchange-dominated spin waves have nanometer wavelength and propagate faster than the dipolar waves. However, the shorter waves are difficult to excite in practice and their propagation distance is very short as well. Therefore, for technical applications, the dipole-dominated spin waves are utilized mostly. A useful approximation to the dipole-dominated FVMSW dispersion relation is given by[36]

Figure
In spin wave devices for signal transmission and processing, such as logic devices and microwave devices, the information carried by the spin waves is considered to be coded in terms of their phases. Therefore, accurate phase manipulation is important for spin wave devices. For standard methods of spin wave excitation and detection by means of microwave microstrip antennas or coplanar waveguides, the phase shift of the spin waves at a given magnetic field can be written as φ(f) = k(f)x, where f is the frequency of the spin waves and x is the distance between the input and output microstrip antennas. The variation of the phase shift is given by Δφ (Δf) = Δk(Δf)x, where Δk is the variation of the spin wave wavenumber. Δk is a function of the variation of spin wave frequency Δf, and this function can be theoretically calculated using the spin wave dispersion relation. For FVMSW, the relationship between Δ fFVMSW and Δk can be theoretically calculated by Eq. (
In summary, 3 μm-thick YIG films were grown on GGG (111) substrates by liquid-phase epitaxy. The relaxation of ferromagnetic resonance (fr) and forward volume spin waves frequency (fFVMSW) shift of vertically magnetized YIG films was studied. It is revealed that a long time relaxation of fr and fFVMSW occurs in the YIG films. The resonance frequency reduces rapidly at the beginning and then tends to a fixed value after a few minutes. Moreover, the stronger the magnetic field is, the shorter the relaxation time becomes. This can be explained by the magnetization relaxation of the pinning layer at the YIG/GGG interface. The phase shift caused by the frequency shift will adversely affect the vertical operation of spin wave devices. The thickness of the pinning layer is estimated to be about 9.48 nm to 15.46 nm.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |