† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51701095 and 51771185) and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20170798).
The interactions of solute atoms with vacancies play a key role in diffusion and precipitation of alloying elements, ultimately influencing the mechanical properties of aluminum alloys. In this study, first-principles calculations are systematically performed to quantify the solute–vacancy interactions for the 3d–4p series and the 4d–5p series. The solute–vacancy interaction gradually transforms from repulsion to attraction from left to right. The solute–vacancy binding energy is sensitive to the supercell size for elements at the beginning. These behaviors of the solute–vacancy binding energy can be understood in terms of the combination and competition between the elastic and electronic interactions. Overall, the electronic binding energy follows a similar trend to the total binding energy and plays a major role in the solute–vacancy interactions.
Due to high specific strength, good abrasion, corrosion, and impact resistance, aluminum and its alloys are widely used in various areas such as aerospace and automobile industries.[1] To satisfy the requirements for the mechanical properties, the aluminum alloys are primarily strengthened by aging hardening with the addition of alloying elements. The interaction between vacancies and solute atoms is a key factor in understanding the basic physical processes, such as diffusion of solutes and other species, segregation, ordering, etc. Those processes are of significance for the aging hardening behavior. Moreover, the elucidation of the origin for the solute–vacancy (hereafter, a vacancy is denoted by □) interactions is indispensable for designing the future high strength or new performance aluminum alloys. The energetic bindings between the vacancies and the solute atoms have been widely studied experimentally[2–6] and theoretically.[7–9] However, there exist some discrepancies in the reported experimental values due to the different techniques utilized and the reliabilities of the measurements. The difference in the calculation methods and parameters gives rise to the discrepancy in theoretical solute–□ binding energy. Moreover, it is still not clear how the physical factors control the solute–vacancy interactions.
Generally, the solute-point defect interactions are governed by two primary factors, i.e., the electronic effect and the strain-relief effect. The effect of electronic structure and atomic distortion on the solute–□ interaction have been widely investigated in Fe,[10,11] W,[12] and Mg.[13] However, the role of electronic structure and the solute size in controlling the solute–□ interactions has not been fully unraveled in aluminum. Hoshino et al. understood the repulsive interaction of a vacancy with 3d and 4d impurities by the breakup of the strong sp–d bonds whereas the attractive interaction might be attributed to the energy gain due to the formation of stronger sp–sp bond.[9] Wolverton studied the dependence of solute–□ binding energy on solute size for the widely used 24 kinds of solutes in aluminum and found the close correlation between binding energy and the solute size for each of Cd, In, Sn, Sb, Pb, and Bi.[7] However, the effects of solute size on binding energy for other elements are still unclear. The role of electronic interaction in the solute–□ interactions was not taken into account.
In the present study, we carry out systematic first-principles calculations to investigate the binding energy values between the 3d, 4p, 4d, 5p solutes and the vacancies in aluminum, which are further decomposed into distortion and electronic binding energy in order to clarify the dominant physical factors that control the solute–□ interactions.
First-principles calculations were performed within the framework of density functional theory (DFT) with the generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) type[14] by using the Vienna ab initio simulation package (VASP).[15,16] The interactions between the ions and valence electrons were described by the projector augmented wave (PAW) method.[17,18] A supercell in a face-centered cubic (fcc) structure was built with 3 × 3 × 3 unit cells, composed of 108 lattice sites. The Brillouin zone was sampled by the Monkhorst–Pack scheme with a 6 × 6 × 6 k-point mesh.[19] A plane wave cutoff of 400 eV was used. The relaxations of atomic position and optimizations of the shape and size of the supercell were implemented. The structural optimization was truncated when the forces converge to less than 0.01 e/Å.
The vacancy formation energy 



The binding energy of the vacancy and solute is defined as

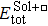

To verify our first-principles calculations, we investigate some fundamental properties of Al by calculating the lattice constant, bulk modulus, and vacancy formation energy. In addition, the binding energy between solutes Mg, Si, and the vacancy (
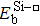
| Table 1. Fundamental properties of Al. Lattice constant a, bulk modulus B, vacancy formation energy |
Figure
 | Fig. 2. Variations of solute–□ binding energy of (a) 3d and 4p, and (b) 4d and 5p elements in fcc Al with atomic number. Other DFT results from Refs. [7,8] are also included. |
It is worth noting that for the 3d–4p and 4d–5p series the energy values for the late elements are impressively the same while there exist noticeable discrepancies for the elements in the beginning. The repulsive reactions are lower than those estimated by Simonovic and Sluiter,[8] whereas the repulsive bindings are highest in the work from Wolverton.[7] Simonovic and Sluiter have reproduced Wolverton’s results by changing the number of k-points.[8] Comparing the calculation parameters with the previous results,[7,8] we find that a dominant discrepancy originates from the supercell size. The 108-atom supercell is utilized in the present study whereas the supercell containing 64 atoms has been built in the published work. Here, the supercells with different sizes are also used to calculate the binding energy of Ti, V, and Zr, as well as Ge and Sn for comparison.
As shown in Table
| Table 2. Comparison of solute–□ binding energy values (in units of eV) for Ti, V, Zr, Ge, Sn between supercell sizes containing 64 atoms and 108 atoms. . |
Generally, the solute–□ interaction is mainly ascribed to the elastic and electronic interactions. In this way, the total binding energy can be decomposed into elastic binding energy 

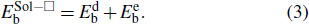



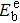
Firstly, to reveal the effect of supercell size on the elastic and electronic interactions, we further calculate the elastic binding energy and electronic binding energy of solutes Ti, V, Zr, Ge, and Sn in the case of 108-atom and 64-atom supercells. As shown in Fig.
 | Fig. 3. Comparison of overall solute–□ binding energy    |
Figure
 | Fig. 4. Variations of distortion binding energy (   |
As far as the elastic interaction is concerned, it is suggested that undersized (oversized) solutes, i.e., those solute atoms with smaller (larger) atomic volume than the host atoms, cause the lattices to contract (expand), whereas the vacancies lead the lattices to shrink.[26,27] The addition of solute elements with different lattice constants will result in lattice-mismatching-induced strain, and thus raising the energy of the host.[28] However, the internal strain may be cancelled to a certain extent by the association of the oversized solute and vacancy. Therefore, the vacancy will be attractive to the oversized solute and repulsive to the undersized solute. These are confirmed by our calculations. Figure

 | Fig. 5. Variations of atomic volume Ω and solute volume Vsol of (a) 3d–4p; (b) 4d–5p solutes with atom number. |
Figure
The electronic effect is encompassed in the electron redistribution. The differential charge density for solute–□ binding is calculated in the cases of Nb, Cu, and Sb. As shown in Fig.
In this work, systematic first principles calculations are carried out to investigate the 3d, 4p, 4d, 5p solute–□ interactions in fcc Al. The solute–□ interactions gradually transform from repulsion to attraction from left to right for the 3d–4p and 4d–5p series. The evolution trend is consistent well with the variation trends of previous theoretical results. The energy values for the late elements show high consistency whereas noticeable discrepancies are observed for the initial elements, which arises from the difference in supercell size. The origin of the solute–□ binding energy behaviors is discussed from the viewpoints of the elastic interaction and electronic interaction. Overall, the variation of electronic binding energy follows a similar trend as that of the total binding energy and plays a major role in the solute–□ interaction. The elastic interaction of the solute–□ pair is repulsive for the undersized solutes but attractive for the oversized solutes. The elastic binding energy is linearly related to the solute volume.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |






