Cite this Article
Bao Na-Na, Huang Yao, Barr Jayson, Luo Zheng-Ping, Wang Yue-Hang, Chen Shu-Liang, Xiao Bing-Jia, Humphreys David. Tests of the real-time vertical growth rate calculation on EAST. Chinese Physics B, 2020, 29(6): 065204  
Permissions
Tests of the real-time vertical growth rate calculation on EAST
Bao Na-Na1, 2, Huang Yao1, †, Barr Jayson3, Luo Zheng-Ping1, Wang Yue-Hang1, Chen Shu-Liang1, Xiao Bing-Jia1, 2, Humphreys David3
Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China
University of Science & Technology of China, Hefei 230026, China
General Atomics, P. O. Box 85608, San Diego, CA 92186-5608, USA

 

† Corresponding author. E-mail: yaohuang@ipp.ac.cn

Project supported by the National MCF Energy Research and Development Program of China (Grant No. 2018YFE0302100) and the National Natural Science Foundation of China (Grant Nos. 11705239, 11805236, and 11875291).

Abstract

In order to measure controllability of vertical instability in EAST, the calculation of model-based vertical growth rate, called rt-gamma, has been successfully carried out in real time. The numerical computing method is adapted from rigid plasma response model in TokSys, which is a widely-used analysis tool for tokamak devices in Matlab environment, but the code is rewritten by taking advantage of GPU parallel computing capability to accelerate the computation. The calculation of rt-gamma is validated by comparing it with the corresponding result generated by TokSys for totally 3508 cases. It is shown that the average absolute value of relative errors is about 0.85%. In addition, the calculation program of rt-gamma has been successfully applied during 2019 EAST campaign. The comparison with experimental results is discussed in this paper. The real-time calculation tool is well able to calculate model-based vertical growth rate, which is convenient for fast and continuous evaluations of EAST control system stability performances.

PACS: ;52.55.Fa;;07.05.Dz;;12.20.Fv;
Keyword:;EAST;;vertical growth rate;;rigid plasma response model;
1. Introduction

Tokamak plasma with elongated cross section is intrinsically unstable, bringing vertical instability to cause vertical displacement event (VDE), leading to vertical unstable disruption, and producing severe damages to devices.[1,2] The experimental advanced superconducting tokamak (EAST) is the first full superconducting tokamak,[3,4] where the elongated plasma cross section is used to enhance plasma confinement performance. Therefore, plasma vertical stabilization is one of the most favorite research on EAST.[5,6] Thanks to the stabilization effect of induced currents in passive structures, passive conductors (for example vacuum vessel) can slow down the plasma motion brought by vertical instability from the very fast Alfvén timescale (typically microseconds) to electromagnetic timescale (typically milliseconds).[7] Thus, active feedback vertical controller cooperating with plasma shape and position controller, can be designed to further suppress vertical instability.[8] The design of feedback controller is usually based on plasma response models. The linear rigid plasma response model in TokSys,[9] which is an important and widely-used tool developed by DIII-D team for tokamak data analysis, has been commonly used in EAST control system. TokSys has been frequently used to calculate growth rate of vertical instability based on rigid plasma response model for the reconstructed plasma equilibrium,[7] which is a key parameter to indicate vertical instability.[10–12] Currently, the real-time version of vertical growth rate calculation (rt-gamma) has been carried out on EAST, which also adopts rigid plasma response model.[13] The computation of rt-gamma is achieved by linearizing the plasma response around the real-time plasma equilibrium reconstructed by PEFIT.[14] Furthermore, a proper representation of passive conductor structures surrounding plasma is required. An equivalent axisymmetric model, taking three-dimensional (3D) features of the conducting structures into account, is proposed in Ref. [15]. For the purpose of a faster computation, a simplified version of this model is utilized in our work. The real-time calculation tool takes advantage of parallel computing provided by graphics processing unit (GPU) and multi-thread techniques. Besides, data transmission with EAST plasma control system (PCS)[16,17] is realized through using reflective memory (RFM) communication method.

In this paper, the availability of the real-time vertical growth rate calculation is verified by comparing it with corresponding TokSys results. The calculation of rt-gamma has been implemented successfully on EAST. During 2019 EAST campaign, several open-loop experiments have been carried out, where the elongated unstable plasma can drift freely in the absence of active vertical control at a predetermined time instant. Experimental vertical growth rate is measured and compared with value of rt-gamma.

The remainder of the paper is organized as following. In Section 2, the calculation of the real-time vertical growth rate is introduced. In Section 3, comparisons of real-time calculation with TokSys results are presented. Experimental results are described in Section 4. Finally, summary and perspective are given in Section 5.

2. The calculation of real-time vertical growth rate

In this section, an introduction to the calculation of real-time vertical growth rate is given, including the computing principle, and its real-time implementation.

2.1. The computing principle

The calculation of rt-gamma is based on the rigid plasma response model.[7] Plasma is considered as a rigid massless filament, carrying current (Ip), only moving in radial (R) and vertical (Z) directions; Plasma filament can maintain force balance at equilibrium point; Plasma filament can be coupled with surrounding conductor structures. The EAST control system can be described using two circuits equations based on the Kirchhoff’s circuit law and Faraday’s law, which are shown in the following.[9]

The circuit equation for plasma and surrounding stabilizing conductors:

where Xss and Xsp refer to variations in conductor flux, due to plasma motion in response to conductor current variation and plasma current variation, respectively.

The circuit equation for plasma:

where Xpp and Xps describe variations of plasma flux due to plasma motion in response to plasma current variation and conductor current variation, respectively.

In the above equations, the subscripts s, p, and c denote stabilization structures, plasma, and the centroid of plasma current; L and M represent self-inductance and mutual inductance; Rc and Zc are the radial and vertical positions of plasma current centroid; Rss Rp represent resistances of stabilizing structure conductors and plasma; Is0 and Ip0 are currents at the initial equilibrium point. The above two first order differential equations can be reorganized into an input equation in the state space form

where

The output equation in the state space form can be written as follows:

Matrices A, B, C, and D are the coefficient matrices in this state space form. x is the state vector and u is the input vector. Because the problem of our concern is plasma vertical instability, y and u can be appointed as the vertical position of plasma and the command for power supply of IC (In-vessel Copper) coil. When there exists any positive real eigenvalue of matrix A, it indicates that the open-loop system (i.e., u = 0) is unstable. For the modelled EAST system at an equilibrium point, there is only one positive eigenvalue of matrix A, representing growth rate of vertical instability.

This computing principle used in rt-gamma calculation is the same as that in TokSys. The main difference between two calculations is the implementation method. Previous calculation of vertical growth rate from TokSys is based on plasma equilibrium generated by EFIT[18] at a time in Matlab environment. Our new calculation of vertical growth rate, i.e., rt-gamma, is more effective. Because the program is rewritten using C and CUDA C languages based on plasma equilibrium produced by PEFIT, which is the GPU parallel equilibrium reconstruction code.

2.2. Implementation of the real-time calculation

Based on the above fundamental principle, the calculation of rt-gamma can be developed taking advantage of GPU acceleration. The flow chart of calculations is given in Fig. 1. In our work, plasma equilibrium is reconstructed by PEFIT, which has been routinely providing magnetic equilibrium solution with 129 × 129 spatial grids for real-time plasma equilibrium and shape control in EAST operation. Besides, a simplified EAST passive structure model, including vacuum vessel structures and coils, is used. Then, the state space equation of the EAST magnetic control system can be built according to Eqs. (1)–(4). Therefore, the vertical growth rate (γ) can be obtained by solving the eigenvalue equation. The determinant | A – αI| is equal to zero, i.e., det (A – αI) = 0, where I represents the identity and α represents all eigenvalues of matrix A. γ is the only positive value among values of α. It can be calculated by searching for the maximum value of α.

Fig. 1. The simplified calculation flow chart. represents the modelled EAST system at an equilibrium point (refer to Subsection 2.1); α represents all eigenvalues of matrix A; γ represents the model-based vertical growth rate.

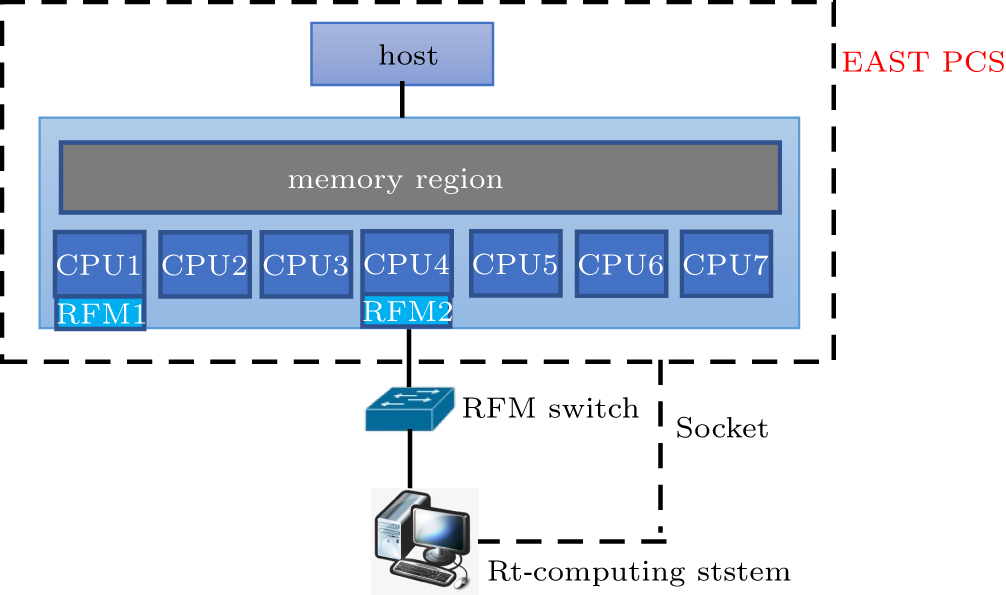
In order to carry out calculations of γ continuously during a discharge, a real-time computing system is designed. The hardware structure of the system, named as “Rt-computing system”, is shown in Fig. 2. EAST PCS, which is within the same software infrastructure of the DIII-D PCS,[19,20] has regularly served for plasma operation campaigns on EAST. The Rt-computing system is connected with EAST PCS through the RFM Internet, therefore it can be considered as an extended system of EAST PCS. CPU (central processing unit) of real-time computing system is equipped with GPU via a PCIe bus, which contributes to the accelerated calculation by using the parallel computing capability. In addition, RFM card, which is an ultra-high speed optic fiber network product, allowing I/O and calculation processing to be run at the same time, is installed in the real-time computing system, which supports analog data to be transferred with EAST PCS.

Fig. 2. The hardware structure of the Rt-computing system. It is connected with EAST PCS through RFM Internet. EAST PCS has one host and one real-time computing node (CPU1–CPU7), connected by high speed 10-Giga bit Ethernet.

The Rt-computing system is able to receive the magnetic diagnostic signals, including the signals of flux loop (38), magnetic probes (36), and the Rogowski coil (1) from EAST PCS, and send the calculation results to EAST PCS in real time. In addition, this system can receive the signal of triggering the shot using Linux Socket communication technique. Real-time data transmission and main calculations of rt-gamma in this system are as follows:

The digital magnetic diagnostic data are transferred to this system from EAST PCS using direct memory access (DMA) method through RFM;

PEFIT computes the plasma equilibrium using these diagnostic data;

The circuit equations (Eqs. (1) and (2)) can be established on the basis of reconstructed equilibrium from PEFIT and EAST passive structure data, thereby matrix A is obtained;

By solving the maximum eigenvalue of matrix A, the vertical growth rate (γ) can be calculated.

Time for computing a γ result is about 2 ms (see the Ref. [13] for more details).

3. Comparisons with TokSys

TokSys, which is well able to estimate vertical growth rates, has been applied to several devices, such as DIII-D[9] and EAST,[5,10–12] and experimentally validated. This gives us the possibility to compare rt-gamma with the result calculated by TokSys directly. For this purpose, a total of 3508 cases, which cover the whole range of interest for EAST experiments from the minimum growth rate (around 100 s−1) to the maximum growth rate (about 800 s−1), are used to compare γ generated by two calculation tools. In these cases, magnetic diagnostics (i.e., flux loop, magnetic probes, and the Rogowski coil) are used as input. For calculations of γ in TokSys, executions are divided into two steps: Firstly, EFIT generates plasma equilibrium according to these diagnostic signals; Then, TokSys calculates γ based on the equilibrium data. As described in the previous section, rt-gamma calculation can be executed in only one step, because the program is embedded with equilibrium reconstruction function (PEFIT). It is obvious that the computation of rt-gamma is more convenient and significantly time-saving in terms of steps to be executed. Comparisons between rt-gamma and TokSys results are presented in Fig. 3. In Fig. 3(a), it is found that the results from these two codes are very close to each other. The absolute relative errors for most cases are less than 3%, the average absolute value of relative errors is 0.85%, and the standard deviation is 0.0102. In Fig. 3(b), relative errors for different γ values (between 100 s−1 and 800 s−1) are mostly within ± 2%. It is shown that the calculation results are in good agreement and the differences are within an acceptable range. Thus, we can confirm that the rt-gamma calculations is able to reliably carry out calculation of vertical growth rate for a wide range of experimental data.

Fig. 3. (a) Bar chart of the number of cases. (b) Relative errors for different vertical growth rates. The red line represents average error. Relative error = (rt-gamma-Toksys)/rt-gamma × 100%.
4. Experiment
4.1. VDE experiment and measurement

An open-loop control experiment is used to better illustrate physical meaning of rt-gamma experimentally. Firstly, on the basis of understanding how vertical stabilization system works, we explain the implementation of this open-loop control experiment on EAST. As we known, plasma is inherently vertically unstable. In that case, there are 2 anti-series IC coils to form the IC circuit for fast response to vertical instability, serving as the vertical stabilization (VS) system. Besides, there are 14 ex-vessel poloidal field (PF) superconductive coils connected to form 12 independent PF circuits for plasma shape and position control system. Thanks to the frequency separation approach by using a filter, vertical position control can be divided into two parts: Vertical stabilization control is done by VS system on a faster time scale; Plasma shape and position control are performed in PF circuits on a slower time scale. During 2019 EAST campaign, these open-loop VDE experiments were conducted by setting command of IC power supply to zero, but remaining other control commands fixed at some point. In that way, after the switch-off of vertical control, elongated plasma became vertically unstable, and i) drifted freely or ii) disrupted quickly in a few milliseconds. It is worth noting that only in the first case (free drift), experimentally measured vertical growth rate can represent realistic plasma vertical motion.

The method of measuring experimental growth rate of vertical instability is given. When vertical control is turned off and plasma drifts freely, its vertical position is shown as a function of time. On EAST, plasma vertical position (Z) is considered as the vertical position of plasma current centroid. It is a real-time estimation by multiplying quantities of magnetic diagnostics by a constant matrix (called E matrix in EAST PCS[8]). So that experimental growth rate can be obtained by fitting time evolution of Z, with the following exponential function:

where Z0 is the initial plasma vertical position at the time t0. γ and δ denote experimental vertical growth rate and a constant coefficient. The initial time t0 represents the switch-off time. Once the time evolution of plasma vertical position, the initial time, and position are known, the values of γ and δ can be solved by fitting experimental data.

4.2. Results and discussion

The discharge #95144 is a typical open-loop experiment, where the vertical control is turned off at 7.7 s. Experimental results during shot #95144 are shown in Fig. 4. We can find evolutions of plasma shape after the cut of vertical feedback control in Fig. 4(a). It is shown that plasma drifts vertically downward, then contacts with the wall, and eventually ends with disruption. In Fig. 4(b), time evolutions of three plasma parameters, i.e., plasma current (Ip), rt-gamma (γ), and vertical position of plasma current centroid (Zc), are presented. The value of rt-gamma is nearly 660 s−1, and plasma vertical position changes significantly around 7.7 s. In the third panel of Fig. 4(b), we can find plasma drifts freely for a few milliseconds, so that experimental vertical growth rate can be measured by fitting the evolution of plasma vertical position using Eq. (5). The initial time t0 is chosen as 7.7 s, and the initial vertical position Z0 is equal to Zc(t0). Experimental vertical growth rate (γ) is approximately 821 s−1 during a time interval of nearly 6 ms. The difference between theoretical calculation of rt-gamma and experimental result are within an acceptable range. As we discussed in Section 2, rt-gamma represents vertical instability of EAST control system model without input, which is consistent with the experimental growth rate of vertical instability in open-loop discharge.

Fig. 4. (a) The evolution of plasma shape after the cut of VS system. (b) The evolutions of plasma current (red line), rt-gamma (green line), vertical position of plasma current centroid (blue line), and fitted evolution of vertical position (rose red line).

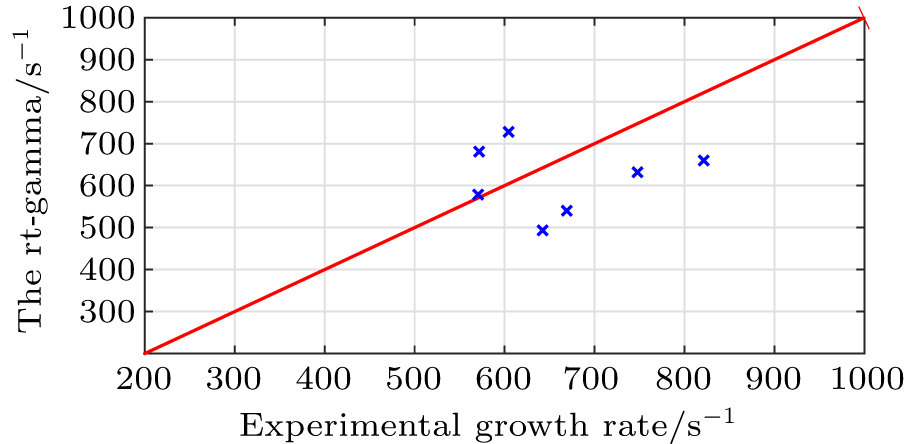
In fact, closed-loop vertical control experiments are usually carried out on EAST from the safe operation point of view. Furthermore, discharge of open-loop control without early vertical disruption, especially for plasma with large elongation, is hard to be guaranteed. Thus, it is very difficult to find such a perspective plasma behavior as that during 6 ms of time interval in shot 95144 for measuring experimental γ. These objective conditions do not allow ideal comparison between model and experimental results in a certain degree. Nonetheless, we still carry out a series of comparisons of rt-gamma with experimental fitted growth rate, based on different kinds of VDE experiments. In these discharges, plasma is approximately considered to drift freely. Common characteristic of plasma for all these discharges is that, plasma vertical position varies exponentially for a few centimeters (for example, 4 cm) during a time interval of a few milliseconds (for example, 6 ms) before disruption. The relationship between model-based result, i.e., rt-gamma, and experimental result is shown in Fig. 5. The points are taken from different shots. The rt-gamma calculation is found to be close to experimental growth rate in these seven shots. The rt-gamma calculation appears to be able to predict the growth rate of vertical instability correctly.

Fig. 5. The rt-gamma versus experimental growth rate.
5. Summary and perspective

In this paper, we firstly introduce the calculation of rt-gamma, which makes use of the rigid plasma response model in TokSys. To achieve an effective computation, the program is rewritten taking advantages of GPU parallel computing capability, which is based on two basic modules, i.e., real-time plasma equilibrium provided by PEFIT and the simplified EAST passive structure. To achieve real-time implementation, the communication with EAST PCS is realized by RFM and Linux Socket techniques.

Secondly, the comparisons with TokSys results covering a wide range of experimental data show the validity of the rt-gamma calculation. Therefore, we confirm rt-gamma calculation is applicable for evaluating model-based vertical growth rate. The value of rt-gamma can be used as a real-time parameter for further controller design or optimization and EAST system stability analysis.

Finally, we describe experimental operation and method of measuring vertical growth rate in detail. The comparison of rt-gamma with experimental results is also presented. The values of rt-gamma are similar to experimental results in our cases. There are varieties of factors causing inconsistencies between theoretical and experimental results, including limitations of rigid plasma response model and the simplified passive structure model, uncertainty in estimating plasma vertical position, and noise and disturbance of plasma, etc. All of these factors may contribute to the understanding of plasma vertical instability. However, it is still a big challenge to accurately model the plasma behavior for vertical instability, which should be emphasized in future studies.

Reference
[1] Hender T C Wesley J C Bialek J et al. 2007 Nucl. Fusion 47 S128
[2] Hassanein A Sizyuk T Ulrickson M 2008 Fusion Eng. 83 1020
[3] Wan B N International Collaborators 2009 Nucl. Fusion 49 104011
[4] Li J Guo H Y Wan B N Gong X Z Liang Y F Xu G S Gan K F Hu J S Wang H Q Wang L Zeng L Zhao Y P Denner P Jackson G L Loarte A Maingi R Menard J E Rack M Zou X L 2013 Nat. Phys. 9 817
[5] Liu L Xiao B J Humphreys D A Luo Z P Chen S L 2014 Fusion Eng. 89 563
[6] Albanese R Ambrosino R Castaldo A De G Luo Z P Mele A Pironti A Xiao B J Yuan Q P 2017 Nucl. Fusion 57 086039
[7] Lazarus E A Lister J B Neilson G H 1990 Nucl. Fusion 30 111
[8] Yuan Q P Xiao B J Luo Z P Walker M L Welander A S Hyatt A W Qian J P Zhang R R Humphreys D A Leuer J A Johnson R D Penaflor B G Mueller D 2013 Nucl. Fusion 53 043009
[9] Humphreys D A Ferron J R Bakhtiari M Blair J A In Y Jackson G L Jhang H Johnson R D Kim J S LaHaye R J Leuer J A Penaflor B G Schuster E Walker M L Wang H Welander A S Whyte D G 2007 Nucl. Fusion 47 943
[10] Qian J P Wan B N Shen B Xiao B J Sun Y W Shi Y J Lin S Y Li J G Gong X Z 2008 Plasma Sci. Technol. 10 290
[11] Qian J P Wan B N Shen B Walker M L Humpreys D A Xiao B J 2009 Chin. Phys. 18 024302
[12] Qiu Q L Xiao B J Guo Y Liu L Xing Z Humpreys D A 2016 Nucl. Fusion 56 106029
[13] Bao N N Huang Y Xiao B J Yuan Q P Zhuang H D Luo Z P Wang Y H Zhang R R 2020 IEEE Trans. Plasma Sci. 48 715
[14] Huang Y Xiao B J Luo Z P 2017 Chin. Phys. 26 085204
[15] Chen S L Villone F Xiao B J Barbato L Mastrostefano S Luo Z P Guo Y Liu L 2016 Plasma Phys. Control. Fusion 58 025017
[16] Yuan Q P Xiao B J Penaflor B G Piglowski D A Liu L Z Johnson R D Walker M L Humphreys D A 2010 Fusion Eng. 85 474
[17] Xiao B J Yuan Q P Luo Z P Huang Y Liu L Guo Y Pei X F Chen S L Humphreys D A Hyatt A W Mueller D Calabró G Crisanti F Albanese A Ambrosino R 2016 Fusion Eng. 112 660
[18] Lao L L St H E Peng Q Ferron J R Strait E J Taylor T S Meyer W H Zhang C You K I 2005 Fusion Sci. Technol. 48 968
[19] Walker M L Ferron J R Humphreys D A Johnson R D Leuer J A Penaflor B G Piglowski D A Ariola M Pironti A Schuster E 2003 Fusion Eng. 66�?8 749
[20] Humphreys D A Ferron J R Hyatt A W La Haye R J Leuer J A Penaflor B G Walker M L Welander A S In Y 2008 Fusion Eng. 83 193