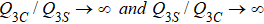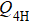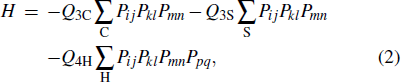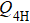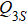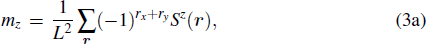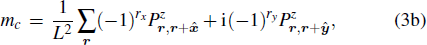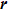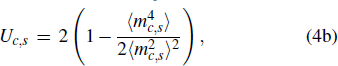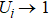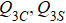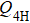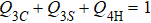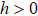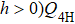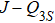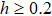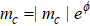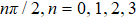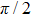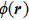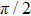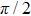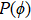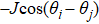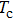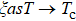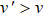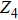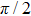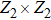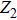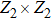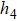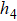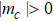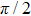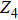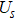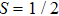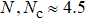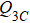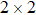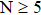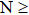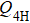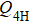1. IntroductionThe spin S = 1/2 Heisenberg model with uniform nearest-neighbor interactions on the two-dimensional (2D) square lattice has a Néel antiferromagnetic (AFM) ordered ground state.[1] By introducing other interactions such as frustration or multi-spin interactions, the quantum fluctuation of the AFM order parameter can be increased, eventually destroying the AFM order and leading to a different ground state. The long-wavelength behavior of Heisenberg and similar quantum magnets can be described field-theoretically by the O(3) nonlinear sigma model with a Berry phase term.[2,3] The Berry phase term will vanish for any smooth spin configurations, i.e., in the AFM phase, but will likely influence the phase diagram of the system if topological defects such as “hedgehog” singularities are considered. In (2+1) dimensions, such effects can play a dominant role and may drive the system into exotic paramagnetic phases, by which we mean collective many-body states with no direct classical analogues (see Ref. [4] for a review).
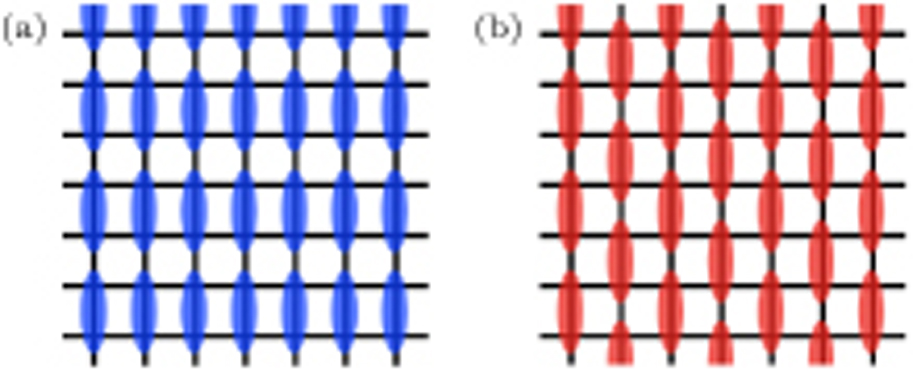
1.1. Valence-bond solidsOne example of an interesting 2D paramagnetic phase is the so-called valence-bond solid (VBS),[5–7] which preserves spin rotational symmetry but spontaneously breaks lattice symmetries through the condensation of singlets forming a regular pattern (or, more precisely, a modulation of the singlet density forms). There are several possible ways to break the lattice symmetries, and therefore VBS phases can also appear in many different incarnations. In this work we discuss two cases of dimer VBSs (i.e., the singlets form between two neighboring spins): the columnar VBS (cVBS) and staggered VBS (sVBS). As shown in Fig. 1, in a cVBS phase the singlets align periodically with no “shifting”, thus breaking the symmetry group of the square lattice p4m down to pmm, while in the sVBS phase the singlets are successively shifted by one lattice spacing and form a stair-pattern. This pattern belongs to the cmm space group. Though the symmetry groups are different, both these VBSs are four-fold degenerate on the infinite lattice or when placed on a torus with an even number of sites in both directions. We will discuss the competition between cVBS and sVBS orderings as well as the quantum phase transitions of these phases into the AFM state.
From the field theoretical perspective, the cVBS phase can be understood as a nontrivial magnetically disordered phase resulting from quantum tunneling of Skyrmions in a certain limit.[6–8] One important consequence of this picture is the deconfined quantum criticality (DQC) scenario.[9] By assuming the conservation of the Skyrmion number at the AFM–cVBS transition, it was proposed that this transition can be described by a CP1 field theory with non-compact U(1) gauge field. There are several interesting and controversial assumptions and consequences of the DQC scenario, e.g., a generically continuous transition where normally a first-order transition would be expected (since the two ordered phases break unrelated symmetries), fractionalized excitations at the critical point, and a “dangerously irrelevant” Z4 perturbing field with an associated emergent U(1) symmetry.[10] This type of order–order phase transition is beyond the conventional Landau–Ginzberg–Wilson (LGW) paradigm and has attracted intensive scrutiny during the past several years.
1.2. Deconfined quantum criticality in spin modelsAs some elements of the DQC scenario are speculative, it is important to realize such phase transitions in concrete microscopic models, to fully test and explore the possible physics arising from the field theoretical proposal and beyond (i.e., features that were not part of the original DQC proposal). Since the sign-problem free J-Q model[11] (with Heisenberg exchange J and a correlated multi-singlet projection Q) was proposed, many detailed studies of the AFM–cVBS transition and the cVBS phase itself have been carried out with quantum Monte Carlo (QMC) simulations of this model[11–24] and of classical 3D models exhibiting analogous transitions.[25–28] These studies solved some previously open questions, but they also posed new ones. For example, observations of emergent higher symmetries at the critical point have been reported recently, with the AFM and cVBS order parameters combining into a larger vector transforming under SO(5)[22,28] or O(4)[29,30] symmetry, depending on the model. The possibility of higher symmetry was pointed out already some time ago[31] and the numerical observations have further spurred the interest in this phenomenon, including in the context of the “web of dualities” between different field theories.[29,32] Furthermore, a description of the transition in terms of non-unitary complex conformal field theories (CFTs)[33–36] was inspired by unusual scaling behaviors observed in J–Q and other models,[13–15,25–27] which by some have been interpreted as signs of an eventually very weakly first-order transition in accessible models, with the critical point existing only in the complex plane. Alternatively, it has also been proposed that the transition is continuous, as in the original DQC scenario, but with unusual scaling behavior stemming from two divergent length scales.[23] It should be noted that there are no unambiguous signs of first-order transitions in the best candidate models, and very recently further evidence has been presented in support of a truly continuous transition.[38] A further intriguing fact is that, in some models where the AFM–VBS transition is clearly first-order, the coexistence state exhibits emergent O(4)[37,39] or SO(5)[40] symmetry, instead of forming two distinct phases separated by tunneling barriers (in analogy with conventional classical co-existence states separated by free-energy barriers).
While the phenomenology of the DQC scenario does not rely on the AFM–VBS transition being strictly continuous (requiring in practice only that the correlation length is very long, which has already been well established), it is still of fundamental interest to try to answer the following basic questions: (i)Are the candidate DQC transitions observed in simulations truly continuous, or do discontinuities and phase coexistence develop on some large length scale? (ii)Is the emergent symmetry of the putative DQC point exact in the thermodynamic limit or does it break down at a finite length scale (i.e., even if the DQC transition itself is truly continuous)? (iii)Are the emergent O(4) and SO(5) symmetries observed in the coexistence states at some first-order AFM–VBS transitions asymptotically exact, or do they break down above some length scale?
These questions are still hard to answer conclusively based on current numerical results [though regarding (i), we again note that Ref. [38] has tilted the scale further toward a continuous transition], because they appear to involve exceedingly large length scales (system sizes). In order to gain deeper understanding of the AFM–cVBS transition, it would be fruitful to construct models that enable tuning of the exotic properties and ingredients addressed in the theory of DQC points, and more broadly in scenarios of weakly first-order transitions with unusual properties. For example, suppressing the possible emergent symmetry of the transition is a promising approach, since it may give rise to a conventional strongly first-order transition that could be detectable with current numerical techniques. If the transitions can be tuned from continuous (or extremely weak first-order), to moderately weakly and strongly first-order, many of the intriguing phenomena listed above could be studied more systematically than what has been possible so far.
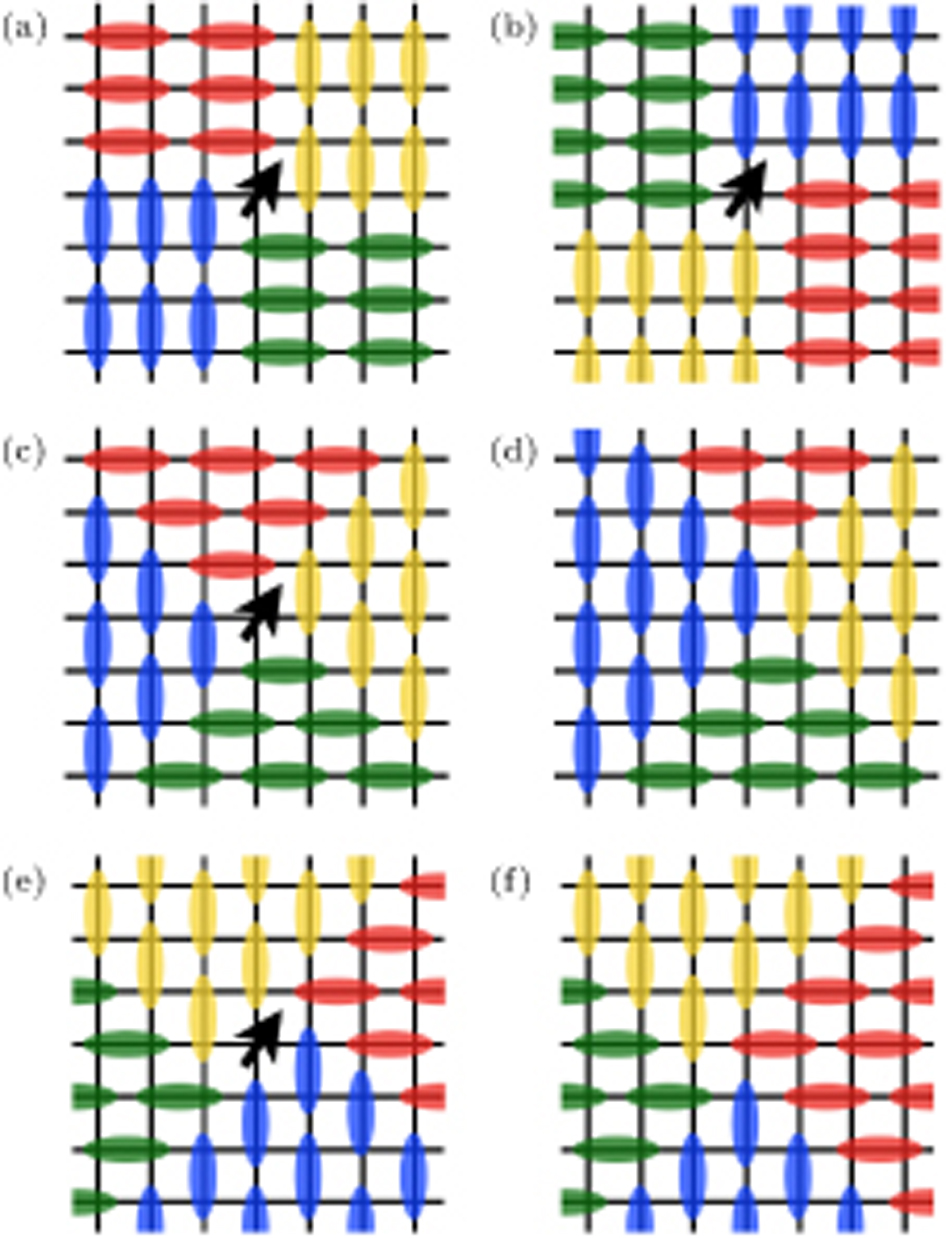
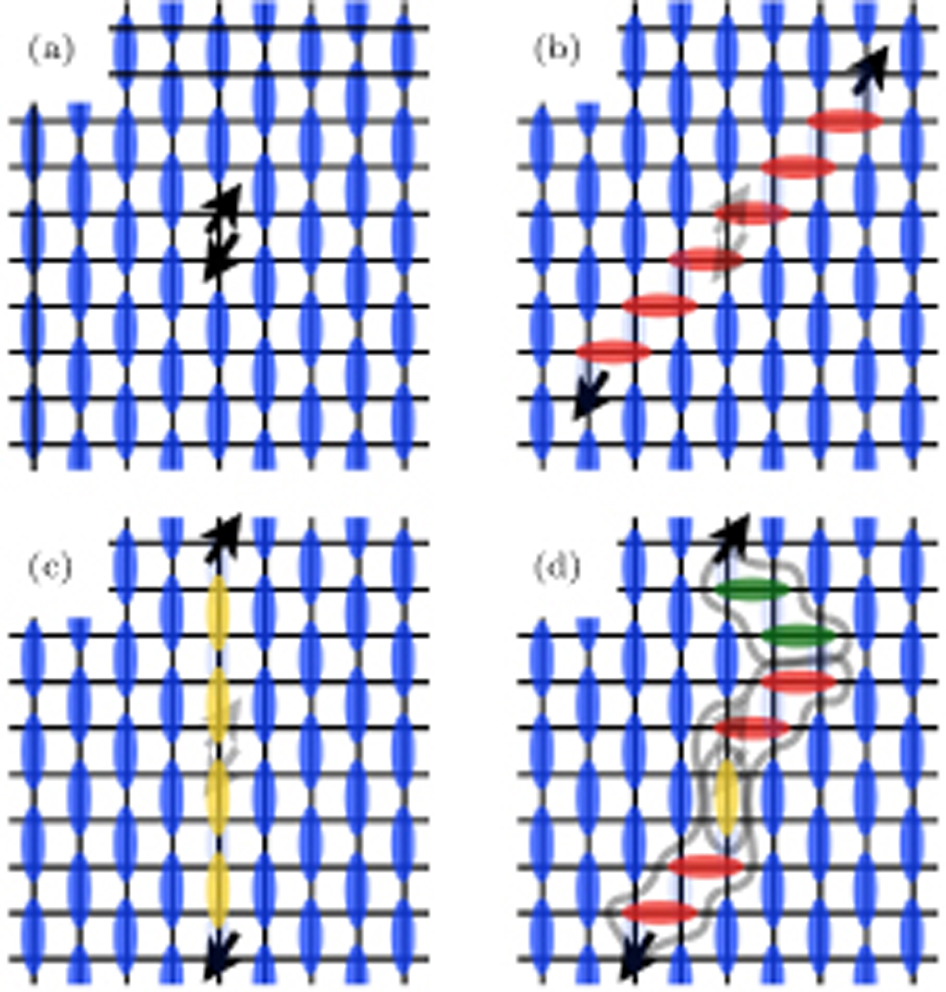
1.3. Vortices and emergent symmetriesThe emergent U(1) symmetry of the DQC scenario [and also the possible higher spherical symmetry like SO(5)] is also related to the properties of the vortices in the VBS state. In the cVBS, a nexus of four domain walls separating the four different dimer patterns must necessarily have an unpaired spin,[10] i.e., the vortex is a spinon. Such spinons are bound into pairs in the cVBS phase and their deconfinement upon approaching the DQC point is directly related to the Z4 vortices evolving into U(1) vortices. Even though the sVBS is also four-fold degenerate, the Z4 vortices in the sVBS can either carry a S = 1/2 spinon or not, as illustrated in Fig. 2. Even if the spinon vortex is realized, unlike the case of the cVBS the dimer pattern will only allow local fluctuations enabling the spinon to propagate in specific directions (in an extreme case of only short dimers). The spinons may then be regarded as a type of fracton — an excitation with constrained mobility — as argued recently for spinons in a plaquette VBS (pVBS).[41] Though in the case of the pVBS the fracton property may only be realized in practice in extreme cases where the four-spin singlets can be regarded as rigid objects, as pointed out in Ref. [40], the phenomenon may actually be more easily realizable in an sVBS.
It would be interesting to investigate whether competing sVBS interactions in a cVBS phase can suppress the fluctuation required for emergent U(1) symmetry and deconfined spinons, thus leading to a different type of AFM–cVBS phase transition. We here desire to affect the properties of the vortices by tuning suitable microscopic couplings. When the sVBS favoring interactions are sufficiently strong they may render the cVBS–AFM transition first-order, unless there is a direct cVBS–sVBS transition. Conversely, the AFM–sVBS transition may possibly become less strongly first-order in the presence of the cVBS favoring interactions.
Studying an sVBS phase and its transition to either an AFM phase or directly into a cVBS phase is interesting in its own right. There have been some discussions regarding phase transitions of the sVBS phase: Vishwanath et al. proposed a possible continuous phase transition in a bilayer honeycomb lattice,[42] and Xu et al. studied certain types of transitions between the sVBS and a Z2 spin liquid or an AFM phase.[43] Numerically, an sVBS state was studied with a J–Q3 model where the three singlet projectors in the Q3 terms are arranged in a staircase fashion for the square lattice.[44] The AFM–sVBS transition in this case as well as in other lattices[45] are very strongly first-order, and the sVBS phase itself exhibits only weak fluctuations from the maximally ordered dimer singlet configuration. Therefore, the model in its current form does not offer many insights into the more interesting case of a strongly fluctuating sVBS where topological defects can play a more prominent role. Considering the possibility of fracton-type spinons and their propensity to nucleate AFM order (in analogy with Ref. [41]), it is, however, not even clear if very strong quantum fluctuations of the sVBS can be achieved before a first-order transition takes place.
1.4. Desired model propertiesSince we are interested in the generic properties of the VBS phases, we will take the approach of “designer Hamiltonians”.[46] The central idea here is to construct an easy-to-study model (e.g., without sign problems in QMC simulations) and to analyze particular phases and phase transitions. The concepts of universality and renormalizaion-group fixed points ensure that the low-energy properties of interest are still of relevance to real-world applications, even though interactions that can be realized in real materials are not faithfully represented microscopically. The following is a list of desired features for the designer Hamiltonian in our study:
harbors all of cVBS, sVBS, and AFM phases;
the cVBS–AFM transition can be tuned from continuous or weakly first-order to more strongly first-order;
realizes a direct cVBS–sVBS transition as well as cVBS and sVBS in parts of its phase diagram.
In previous studies, none of the existing models were able to connect the first-order sVBS–AFM transition and the cVBS–AFM DQC transition, nor could they realize a direct transition between the two VBS states. In this work, we introduce a model Hamiltonian with two competing terms that individually favor a cVBS and an sVBS ground state, respectively, as discussed above. The motivation here is that the presence of the sVBS favoring interactions in the cVBS phase may to some degree suppress the development of the emergent U(1) symmetry that characterizes the DQC transition between the cVBS and the AFM. We will show here that these expectations are borne out by our results for the model we have constructed, in particular as regards the evolution of the AFM–cVBS transition from continuous or very weakly first-order to clearly first-order.
1.5. Article outlineThe structure of the remainder of this article is as follows: In Section 2 we introduce the S = 1/2 [SU(2)] models we study in this work. In Section 3 we extract the phase diagram of the model and discuss the nature of the various quantum phase transitions we have identified. In Section 4 we discuss the SU(N) generalization of our model and present results for N = 3. In Section 5 we summarize our results and discuss some possible further applications of the models.
2. Model and observablesWe start from two previously studied designer Hamiltonians that host cVBS and sVBS phases, respectively. The ground state of a columnar J–Q3C model[17] undergoes a DQC type cVBS–AFM transition, and the ground state of a staggered J–Q3S model[44] exhibits a first-order sVBS–AFM transition. Here and henceforth we use the second subscript on Q to indicate a columnar (C) or staggered (S) spatial arrangement of the three singlet projectors used in the multi-spin interaction. A natural strategy to construct a model that harbors both cVBS and sVBS ground states would be to combine the Q3C terms and Q3S terms as follows:

where
Pij denotes a projection operator to a spin singlet state on sites
i and
j,
Pij = 1/4-

, and the summation indices C and S stand for all arrangements of the six indices
i–m in columns or stairs, respectively. For details of the placement of the indices we refer to Figs.
3(a) and
3(b).
In the two extreme cases where 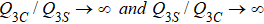 in Eq. (1), the ground state of h would be in the cVBS and sVBS phase, respectively. However, there is not necessarily a direct transition between these two VBS phases with just the terms in the Hamiltonian defined in Eq. (1). As we will see below, there is an AFM phase between them, i.e., AFM order can form as a compromise between the two competing VBS states.
in Eq. (1), the ground state of h would be in the cVBS and sVBS phase, respectively. However, there is not necessarily a direct transition between these two VBS phases with just the terms in the Hamiltonian defined in Eq. (1). As we will see below, there is an AFM phase between them, i.e., AFM order can form as a compromise between the two competing VBS states.
In order to achieve a direct cVBS–sVBS transition, we have to introduce another interaction. The Heisenberg exchange J only strengthens the AFM order and expands the AFM phase between the two VBS phases. We will therefore not further discuss the Heisenberg interaction here and instead consider another type of multi-spin Q-type interaction. From the field theoretical point of view, we would like to turn on some symmetry-allowed relevant terms with respect to the cVBS–AFM fixed point. An interaction achieving our aim is the 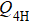 terms with the relative arrangement of the four singlet projectors illustrated in Fig. 3(c), which has some resemblance to the letter H that we use to identify this interaction. By combining it with the two previous terms we obtain
terms with the relative arrangement of the four singlet projectors illustrated in Fig. 3(c), which has some resemblance to the letter H that we use to identify this interaction. By combining it with the two previous terms we obtain
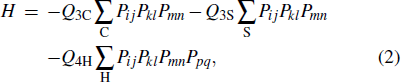
which is the model we study in this paper.
Since the 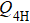 terms are compatible with both cVBS and sVBS orders (i.e., a quarter subset of the terms have all their projectors on the strong bonds in the respective phases), we expect that they should strengthen both the cVBS and sVBS orders, thereby suppressing the AFM phase. This is indeed the case, and, moreover, we will find that
terms are compatible with both cVBS and sVBS orders (i.e., a quarter subset of the terms have all their projectors on the strong bonds in the respective phases), we expect that they should strengthen both the cVBS and sVBS orders, thereby suppressing the AFM phase. This is indeed the case, and, moreover, we will find that  in combination with
in combination with 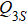 can change the nature of the cVBS–AFM transition from a DQC transition to a clearly first-order transition.
can change the nature of the cVBS–AFM transition from a DQC transition to a clearly first-order transition.
To study all three phases we define their order parameters as follows:
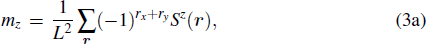
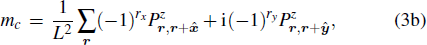

where

runs over all sites of the
square lattice with periodic boundary conditions and

is the z-component of the singlet projector;

, where for convenience we now use the lattice coordinate
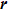
as the index instead of the site label used in the Hamiltonian (2). We can further define the Binder cumulants to capture the characteristic order-parameter distributions in the different phases;

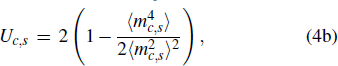
where the coefficients are chosen according to the number of components of the order parameter (and in the case of U
z also taking into account that only one out of three components of the staggered magnetization is used), such that the cumulants approach
1 with increasing
L if there is order of the given type and
0 otherwise. The condition
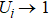
relies only on the presence of long range order, while

in a disordered phase also relies on the fluctuations being Gaussian. As we will see below, there are cases where the fluctuations are not Gaussian even though the correlations are short-ranged.
We used the stochastic series expansion (SSE) QMC method for all the calculations presented here. For details of this algorithm we refer to the review in Ref. [47], which includes an implementation for the conventional J–Q model. The more complicated Q terms used here can be treated with simple generalizations.
3. Numerical resultsTo investigate the ground state phase diagram of the model, Eq. (2), with its three parameters  ,and
,and 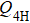 , we consider the plane of two dimensionless coupling ratios (g,h):
, we consider the plane of two dimensionless coupling ratios (g,h):


To fix the energy scale, we always keep
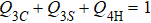
, and in the simulations with this convention we set the inverse temperature to

.
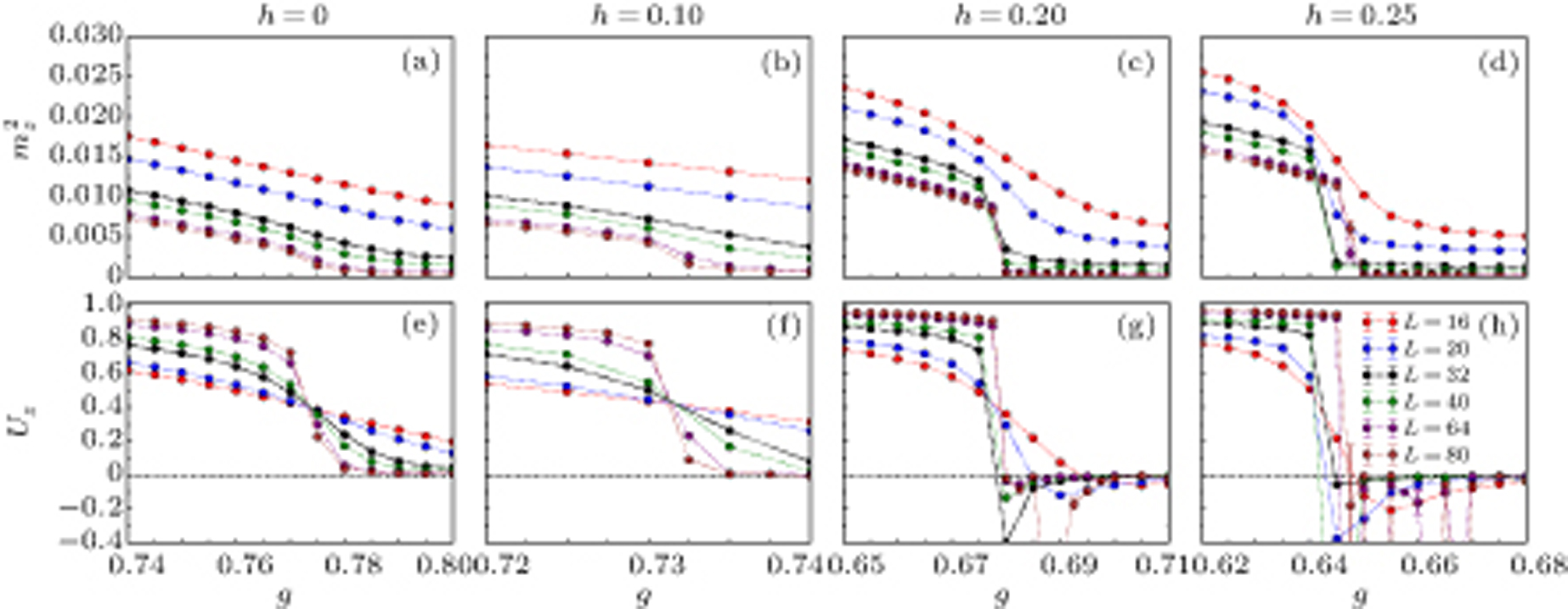
3.1. Phase diagramIn Fig. 4 we present results for the order parameters and Binder cumulants versus g for several values of h. Here we use a rather small system, L = 16, but this already gives us an initial impression about the phase diagram. Figure 5 shows the phase boundaries based on several extracted transition points, using also the results for systems larger than L = 16 close to the transition (some of which are further discussed below), for extrapolating to the thermodynamic limit.
We observe the three different phases as expected. A key feature here is that the  interaction (
interaction (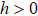 ) indeed shrinks the AFM phase and eventually brings the two VBS phases into contact with each other, thus supporting the intuition that the specific arrangement of the projectors in Fig. 3(c) favors both types of VBS phases while suppressing the AFM phase. The direct phase transition between the two VBS phases, which starts above some value of h close to 0.35, is strongly first-order, as also would be expected on the grounds that the two phases break the lattice symmetry in different ways.
) indeed shrinks the AFM phase and eventually brings the two VBS phases into contact with each other, thus supporting the intuition that the specific arrangement of the projectors in Fig. 3(c) favors both types of VBS phases while suppressing the AFM phase. The direct phase transition between the two VBS phases, which starts above some value of h close to 0.35, is strongly first-order, as also would be expected on the grounds that the two phases break the lattice symmetry in different ways.
The sVBS–AFM transition is always first-order, as is clear from the sharp jumps in both the order parameters and Binder cumulants in Fig. 4 for h = 0.4 and 0.6. The behavior is similar to the previously studied  model.[44] The first-order transition is expected since, as discussed in Section 1, the DQC scenario does not apply to the sVBS state. We only observe a mild reduction of the size of the first-order discontinuities with increasing h. The location of the triple point where all the phases come together still has some uncertainty, due to difficulties with the size extrapolations close to this point.
model.[44] The first-order transition is expected since, as discussed in Section 1, the DQC scenario does not apply to the sVBS state. We only observe a mild reduction of the size of the first-order discontinuities with increasing h. The location of the triple point where all the phases come together still has some uncertainty, due to difficulties with the size extrapolations close to this point.
3.2. Nature of the AFM–cVBS transitionAs discussed in Section 1, the AFM–cVBS transitions in the standard J –Q models (the J–
 and J–Q3C models in the notation used here) are of the DQC type, possibly with extremely weak and currently not detectable discontinuities though a strictly continuous transition appears more likely.[38] The extended model used here does not reduce to the previously studied cases because of the lack of J terms and also because we keep
and J–Q3C models in the notation used here) are of the DQC type, possibly with extremely weak and currently not detectable discontinuities though a strictly continuous transition appears more likely.[38] The extended model used here does not reduce to the previously studied cases because of the lack of J terms and also because we keep  , so that there is always some
, so that there is always some  and (for
and (for 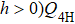 interaction present at the AFM–cVBS transition. Nevertheless, based on the L = 16 results shown in Fig. 4, the transition looks continuous for h = 0 and 0.2 (where there is still an AFM phase). However, in order to determine the true nature of the transition the system-size dependence has to be studied very carefully and on much larger lattices. Here our aim is not to draw definite conclusions, as very significant computational resources are required in order to obtain size-converged critical exponents or, alternatively, to detect weak discontinuities.
interaction present at the AFM–cVBS transition. Nevertheless, based on the L = 16 results shown in Fig. 4, the transition looks continuous for h = 0 and 0.2 (where there is still an AFM phase). However, in order to determine the true nature of the transition the system-size dependence has to be studied very carefully and on much larger lattices. Here our aim is not to draw definite conclusions, as very significant computational resources are required in order to obtain size-converged critical exponents or, alternatively, to detect weak discontinuities.
As an initial study of the AFM–cVBS transition in the extended J–Q model, in Figs. 6 and 7 we present results for AFM and cVBS quantities, respectively. We focus on relatively small h values, h = 0,0.1,0.2, and 0.25, for which the transition is either continuous or weakly first order, and in each case we show results for several different system sizes between L = 16 and L = 80. For h = 0 and 0.1, we find that both order parameters evolve smoothly versus g for all system sizes, while for the larger h values obvious discontinuities develop with increasing L. For the smaller h values the Binder cumulants for different L cross each other in what appears to be a single point (though one should expect some drifts in the crossing points if the behaviors are examined in more detail with high-quality data on a denser grid), which is characteristic for continuous transitions. For the larger h values the cumulants are more strongly varying and also become negative in the neighborhood of the transition. The latter behavior suggests that the cumulants will eventually, for larger system sizes, develop the sharp negative peaks that are characteristic for conventional first-order transitions. Such peaks should asymptotically diverge in proportion to the system volume, as previously observed with the 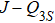 model.[44]
model.[44]
Recently, unconventional first-order transitions with emergent spherical symmetry of the order parameters were identified where negative cumulant values are observed, which can be traced to the lack of tunneling barriers when the two order parameters can be continuously rotated into each other.[37,39,40] The results for 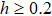 in Figs. 6 and 7 suggest that the transitions here are not of the kind with emergent symmetry (though we have not established the volume-proportionality of the cumulant peak growth). In Subsection 3.3 we will also explicitly confirm that there is no emergent symmetry of the two order parameters. For h = 0 and 0.1, we can only say with certainty that the transitions are less first-order-like than those at the higher h values, as it is possible that discontinuities and negative cumulant peaks develop above some system size that decreases with increasing h.
in Figs. 6 and 7 suggest that the transitions here are not of the kind with emergent symmetry (though we have not established the volume-proportionality of the cumulant peak growth). In Subsection 3.3 we will also explicitly confirm that there is no emergent symmetry of the two order parameters. For h = 0 and 0.1, we can only say with certainty that the transitions are less first-order-like than those at the higher h values, as it is possible that discontinuities and negative cumulant peaks develop above some system size that decreases with increasing h.
Note again that, also at h = 0 there are Q3S interactions present in the (g,h) parameterization of the model that we have used here. It is possible, in principle, that the staggered term alters the DQC transition, though we see no evidence of such behavior here (and the prospect also appears unlikely, as there is no apparent new scaling field that this operator can bring in that is originally absent). To compute the scaling dimension of the Q3S coupling is possible in principle by analyzing the corresponding correlation function at the AFM–cVBS transition of the standard J–Q model. However, with the large number of singlet projectors involved (six in total for the correlation of the QS3 terms) such a calculation would be very challenging[48] and we have not attempted this.
3.3. Fluctuations in the VBS phasesConsider the global cVBS angle ϕ defined from the complex order parameter mc in Eq. (3b) written as 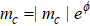 . Starting from one out of the four dimer patterns in the cVBS phase, a series of local dimer flips (i.e., two adjacent parallel dimers rotate spatially by π/2) can gradually shift the angle. Similarly, by replacing a pair of parallel dimers by a superposition of x- and y-oriented dimers (i.e., plaquette singlets), the angle also shifts relative to that with only static columnar dimers. Since the dimer order in the cVBS phase undergoes significant fluctuations (not only of the kind affecting short dimers as discussed above, but the actual state also contains longer bipartite valence bonds), neither the angle ϕ nor the magnitude
. Starting from one out of the four dimer patterns in the cVBS phase, a series of local dimer flips (i.e., two adjacent parallel dimers rotate spatially by π/2) can gradually shift the angle. Similarly, by replacing a pair of parallel dimers by a superposition of x- and y-oriented dimers (i.e., plaquette singlets), the angle also shifts relative to that with only static columnar dimers. Since the dimer order in the cVBS phase undergoes significant fluctuations (not only of the kind affecting short dimers as discussed above, but the actual state also contains longer bipartite valence bonds), neither the angle ϕ nor the magnitude  is fixed, but their values as obtained from SSE configurations fluctuate. The relative size of the fluctuations vanishes as
is fixed, but their values as obtained from SSE configurations fluctuate. The relative size of the fluctuations vanishes as  as long as the system is cVBS ordered in the thermodynamic limit.
as long as the system is cVBS ordered in the thermodynamic limit.
The order parameter can also be defined on some cell of size λ smaller than the lattice size L, and, in the same way as explained above, even in an cVBS state on an infinite lattice the local angle ϕ(r) thus defined in a cell centered at r can take values also between the four columnar angles 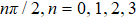 . When crossing a
. When crossing a 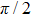 domain wall,
domain wall, 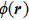 rotates between two adjacent values of n over the width of the domain wall, and such intermediate angles correspond to the presence of resonating valence bonds. In the center of a
rotates between two adjacent values of n over the width of the domain wall, and such intermediate angles correspond to the presence of resonating valence bonds. In the center of a  domain wall between two columnar states the dimer pattern is exactly that of a pVBS state, with resonating pairs of horizontal and vertical dimers forming on a specific plaquette pattern (one out of four possible patterns, depending on which n values the domain wall separates). In the DQC scenario these
domain wall between two columnar states the dimer pattern is exactly that of a pVBS state, with resonating pairs of horizontal and vertical dimers forming on a specific plaquette pattern (one out of four possible patterns, depending on which n values the domain wall separates). In the DQC scenario these 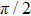 domain walls are indeed favored over π domain walls,[10] as has been explicitly observed in studies of J–Q models[49] (where an induced π domain wall splits up spontaneously into a pair of
domain walls are indeed favored over π domain walls,[10] as has been explicitly observed in studies of J–Q models[49] (where an induced π domain wall splits up spontaneously into a pair of 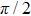 domain walls), and the domain wall thickness diverges as the DQC point is approached from the cVBS side.
domain walls), and the domain wall thickness diverges as the DQC point is approached from the cVBS side.
The domain-wall broadening also corresponds to a lowering of an effective potential  experienced by the global cVBS angle in a finite system, which implies that the distribution
experienced by the global cVBS angle in a finite system, which implies that the distribution 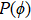 of the global angle becomes increasingly flat as the DQC point is approached. The emergent U(1) symmetry close to the DQC point has been frequently studied by investigating such distributions,[11–13] and the fact that the symmetry has been observed on very large length scale is one of the most important indicators of the DQC phenomenon actually being realized in these models.[4]
of the global angle becomes increasingly flat as the DQC point is approached. The emergent U(1) symmetry close to the DQC point has been frequently studied by investigating such distributions,[11–13] and the fact that the symmetry has been observed on very large length scale is one of the most important indicators of the DQC phenomenon actually being realized in these models.[4]
The emergent U(1) symmetry of the cVBS is analogous to the classical 3D clock models with a potential  (with integer q) added to the standard XY model with nearest-neighbor interactions
(with integer q) added to the standard XY model with nearest-neighbor interactions 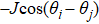 .[10] In the clock models, for
.[10] In the clock models, for  4 the clock term is a “dangerously irrelevant” perturbation, meaning that there is still a phase transition in the standard 3D XY universality class, at some critical temperature
4 the clock term is a “dangerously irrelevant” perturbation, meaning that there is still a phase transition in the standard 3D XY universality class, at some critical temperature 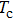 that depends on
that depends on  , but in the ordered state the broken symmetry changes from U(1) to
, but in the ordered state the broken symmetry changes from U(1) to  (i.e., the ordered state corresponds to a different renormalization-group fixed point). The emergent U(1) symmetry is associated with a second divergent length scale
(i.e., the ordered state corresponds to a different renormalization-group fixed point). The emergent U(1) symmetry is associated with a second divergent length scale  , which diverges faster than the conventional correlation length
, which diverges faster than the conventional correlation length 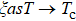 from below. The correlation length and the U(1) length are governed by exponents ν’and ν, respectively, and
from below. The correlation length and the U(1) length are governed by exponents ν’and ν, respectively, and 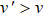 . The exponents are related to each other and to the scaling dimension of the clock perturbation in a way that has been controversial[50–53] and for which new insights were presented very recently.[54] The analogous U(1) length scale has also been studied in the standard J–Q model,[17] though not yet at the level of precision as was possible in the classical case.
. The exponents are related to each other and to the scaling dimension of the clock perturbation in a way that has been controversial[50–53] and for which new insights were presented very recently.[54] The analogous U(1) length scale has also been studied in the standard J–Q model,[17] though not yet at the level of precision as was possible in the classical case.
Here we wish to make some observations regarding the emergent U(1) symmetry of the cVBS state as the transition changes from continuous to first-order when we increase the tuning parameter h (as demonstrated above in Figs. 6 and 7). We note that the symmetry broken by the cVBS is normally regarded as 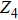 , though strictly speaking, from the purely group-theoretical perspective, it can also be classified as
, though strictly speaking, from the purely group-theoretical perspective, it can also be classified as  , as discussed in detail in Ref. [40]. What qualifies the classification physically as
, as discussed in detail in Ref. [40]. What qualifies the classification physically as  is the nature of the dominant fluctuations between the four degenerate dimer patterns.[10] As discussed above, the elementary domain walls are of the
is the nature of the dominant fluctuations between the four degenerate dimer patterns.[10] As discussed above, the elementary domain walls are of the 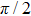 type, and this means that a state with global angle
type, and this means that a state with global angle  most easily tunnels to an adjacent state with
most easily tunnels to an adjacent state with  (on a finite system, where the symmetry is not strictly broken and such fluctuations take place), instead of dominant fluctuations between states with different n of the types
(on a finite system, where the symmetry is not strictly broken and such fluctuations take place), instead of dominant fluctuations between states with different n of the types  . If the latter type of fluctuations were dominant, the symmetry should physically be classified as
. If the latter type of fluctuations were dominant, the symmetry should physically be classified as 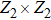 . To be more precise, such fluctuation pattern is equivalent to that when a
. To be more precise, such fluctuation pattern is equivalent to that when a 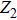 symmetry breaks twice, which should obviously be regarded as
symmetry breaks twice, which should obviously be regarded as 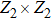 symmetry breaking.
symmetry breaking.
It can be noted that, the classical 3D q = 4 clock model with potential depth  (or, equivalently, the “hard” clock model where the angles are constrained to the strictly horizontal and vertical directions) in fact maps onto two decoupled Ising models, thus breaking the
(or, equivalently, the “hard” clock model where the angles are constrained to the strictly horizontal and vertical directions) in fact maps onto two decoupled Ising models, thus breaking the  symmetry in a phase transition of the Ising type. In contrast, the “soft” q = 4 clock model with small
symmetry in a phase transition of the Ising type. In contrast, the “soft” q = 4 clock model with small  exhibits clock-like fluctuations, and its phase transition is in the XY universality class on account of the emergent U(1) symmetry. The exact value of
exhibits clock-like fluctuations, and its phase transition is in the XY universality class on account of the emergent U(1) symmetry. The exact value of 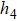 at which the change in fluctuation paths takes place is not known, because of the difficulties in analyzing the emergent U(1) symmetry when the scaling dimension
at which the change in fluctuation paths takes place is not known, because of the difficulties in analyzing the emergent U(1) symmetry when the scaling dimension  of
of 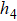 is only very slightly negative (
is only very slightly negative ( ).[21,54]
).[21,54]
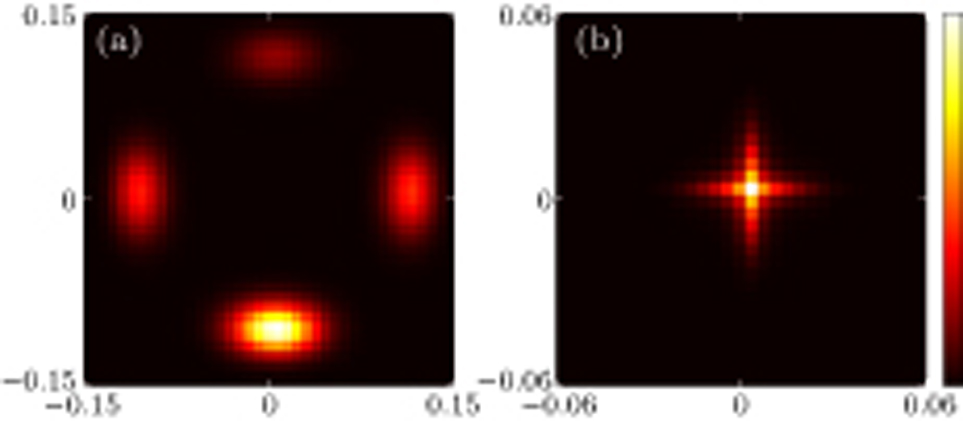
The cVBS state in the conventional J–Q models also exhibits clock-like fluctuations and emergent U(1) symmetry, and is, thus, more similar to the soft q = 4 clock model (though the universality class is different; DQC instead of XY).[11–13] In Fig. 8 we demonstrate these behaviors also for our model at h = 0, where according to the results presented above in Subsection 3.2 the AFM–cVBS transition appears to be continuous. Figure 8(a) is for a case where the system is already quite close to the transition into the AFM state, and for a relatively small system L = 32, where both the angular and amplitude fluctuations are large. The probability density is very low in the center of the distribution, reflecting a robust non-zero magnitude  of the order parameter. The four-fold symmetry is observed clearly even though all angles
of the order parameter. The four-fold symmetry is observed clearly even though all angles  have significant probability density. In Fig. 8(b) the system is closer to the transition but still slightly inside the cVBS phase, as reflected in the fact that the radial distribution still is peaked for
have significant probability density. In Fig. 8(b) the system is closer to the transition but still slightly inside the cVBS phase, as reflected in the fact that the radial distribution still is peaked for 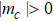 , though now the density at
, though now the density at  is also large. There is still some remnants of
is also large. There is still some remnants of  symmetry here (a slightly diamond-like shape), which would further diminish if we move even closer to the transition. Proper analysis of the size dependence of the distribution[37,40] would be required to draw firm conclusions, but at least it appears plausible here that the system has the emergent U(1) symmetry expected at a DQC transition.
symmetry here (a slightly diamond-like shape), which would further diminish if we move even closer to the transition. Proper analysis of the size dependence of the distribution[37,40] would be required to draw firm conclusions, but at least it appears plausible here that the system has the emergent U(1) symmetry expected at a DQC transition.
It is now interesting to see how the cVBS order parameter distribution evolves as we increase h and enter the regime where the AFM–cVBS transition is clearly first-order. In Fig. 9 we show results at h = 0.2. Here we no longer observe clock-like fluctuations, but instead see significant probability of fluctuations toward the center of the distribution, where in the Z4 case there is very little weight. If these fluctuations would be due to direct migration between the two maxima on the x or y axis, we would conclude that the π domain wall has replaced the 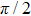 one as the softest domain wall, and, therefore, that the fluctuation paths correspond to
one as the softest domain wall, and, therefore, that the fluctuation paths correspond to  symmetry instead of
symmetry instead of 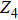 . However, the situation is made more complicated by the fact that coexistence of the AFM and cVBS order parameters at the first-order transition implies fluctuation paths also into the AFM phase if we are sufficiently close to the phase transition. Indeed, upon closer examination of the distribution represented in a higher-dimensional space reveals that the fluctuation paths in Fig. 9 correspond to significant population of the AFM phase, in which of course the cVBS order parameter is small and weight is produced at the center of the distribution. Therefore, from these results we can only conclude that the clock-like
. However, the situation is made more complicated by the fact that coexistence of the AFM and cVBS order parameters at the first-order transition implies fluctuation paths also into the AFM phase if we are sufficiently close to the phase transition. Indeed, upon closer examination of the distribution represented in a higher-dimensional space reveals that the fluctuation paths in Fig. 9 correspond to significant population of the AFM phase, in which of course the cVBS order parameter is small and weight is produced at the center of the distribution. Therefore, from these results we can only conclude that the clock-like  fluctuations are suppressed as the first-order cVBS–AFM transition is approached and, therefore, there are no longer any signs of emergent U(1) symmetry. Further inside the cVBS phase, even for large h, we still observe the clock-like
fluctuations are suppressed as the first-order cVBS–AFM transition is approached and, therefore, there are no longer any signs of emergent U(1) symmetry. Further inside the cVBS phase, even for large h, we still observe the clock-like  fluctuations.
fluctuations.
3.4. sVBS fluctuations in the cVBS phaseThe Binder cumulant results in Fig. 4 show that the value of 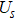 is not close to 0 in the cVBS phase (and also does not approach 0 for larger system sizes), which is at first sight puzzling. Normally an appropriately defined cumulant
is not close to 0 in the cVBS phase (and also does not approach 0 for larger system sizes), which is at first sight puzzling. Normally an appropriately defined cumulant  approaches zero with increasing system size in a phase where there is no order of the X type, on account of Gaussian fluctuations. However, the sVBS fluctuations are not Gaussian-distributed in the cVBS phase, as we show here.
approaches zero with increasing system size in a phase where there is no order of the X type, on account of Gaussian fluctuations. However, the sVBS fluctuations are not Gaussian-distributed in the cVBS phase, as we show here.
Consider the two-dimensional distribution of the complex order parameter  defined in Eq. (3c). Inside the cVBS phase, if the four-fold symmetry is broken and the system is locked into one of the cVBS pattern, the sVBS order parameter is not isotropic, because the columnar bond pattern will favor short-range sVBS order with the dimers oriented in the same (x or y) direction as that in the cVBS pattern. Therefore, the conditional sVBS distribution given one of the sVBS patterns will be elongated in one direction, and when averaging over all the four cVBS patterns a + shaped sVBS distribution is generated. This is demonstrated in Fig. 10 for our model at a point rather deep inside the cVBS phase. Since the + shaped distribution is far from a 2D Gaussian, the cumulant will not approach zero in this case, thus explaining the results in Fig. 4. These arguments also apply to the cVBS fluctuations inside the sVBS phase, and, indeed, in Fig. 4 we can also see that the cVBS cumulant
defined in Eq. (3c). Inside the cVBS phase, if the four-fold symmetry is broken and the system is locked into one of the cVBS pattern, the sVBS order parameter is not isotropic, because the columnar bond pattern will favor short-range sVBS order with the dimers oriented in the same (x or y) direction as that in the cVBS pattern. Therefore, the conditional sVBS distribution given one of the sVBS patterns will be elongated in one direction, and when averaging over all the four cVBS patterns a + shaped sVBS distribution is generated. This is demonstrated in Fig. 10 for our model at a point rather deep inside the cVBS phase. Since the + shaped distribution is far from a 2D Gaussian, the cumulant will not approach zero in this case, thus explaining the results in Fig. 4. These arguments also apply to the cVBS fluctuations inside the sVBS phase, and, indeed, in Fig. 4 we can also see that the cVBS cumulant  is not zero inside the sVBS phase.
is not zero inside the sVBS phase.
4. SU(N) model and results for N = 3So far, the model we have studied was defined with the standard 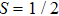 spin operators with SU(2) symmetry. Spin models on bipartite lattices have a natural SU(n) generalization, in which the spins on one sublattice transform under the fundamental representation of the group and the ones on the opposite sublattice transform with the conjugate of the fundamental representation.[6] In the Heisenberg model with only nearest-neighbor Heisenberg exchange, a large-N mean-field-like theory with 1/N corrections predicts that the AFM order vanishes above
spin operators with SU(2) symmetry. Spin models on bipartite lattices have a natural SU(n) generalization, in which the spins on one sublattice transform under the fundamental representation of the group and the ones on the opposite sublattice transform with the conjugate of the fundamental representation.[6] In the Heisenberg model with only nearest-neighbor Heisenberg exchange, a large-N mean-field-like theory with 1/N corrections predicts that the AFM order vanishes above  ,[7] after which the ground state is a cVBS state. QMC simulations for integer n indeed found AFM order up to
,[7] after which the ground state is a cVBS state. QMC simulations for integer n indeed found AFM order up to  and cVBS order for larger N.[55] QMC simulations with loop-type algorithms can also be generalized to non-integer N, and a critical
and cVBS order for larger N.[55] QMC simulations with loop-type algorithms can also be generalized to non-integer N, and a critical 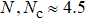 , in good agreement with the
, in good agreement with the  expansion was found.[56] J–Q models generalized to SU(n) have likewise been useful for testing
expansion was found.[56] J–Q models generalized to SU(n) have likewise been useful for testing  expansions within the DQC scenario,[46] and a remarkable agreement has been found between the
expansions within the DQC scenario,[46] and a remarkable agreement has been found between the  results and QMC finite-size scaling results for moderate values of N.[57,58]
results and QMC finite-size scaling results for moderate values of N.[57,58]
Given that larger N drives the Heisenberg and J–Q systems toward VBS ordering, in the model studied here we would expect the AFM phase to shrink upon increasing N. Here our aim is just to demonstrate this behavior, and we leave more detailed studies to future work. Using N = 3, we set h = 0, i.e., we only have the competing 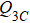 and
and  left, as in the Hamiltonian Eq. (1).
left, as in the Hamiltonian Eq. (1).
As shown in Fig. 11, the SU(3) system undergoes a clearly first-order direct sVBS–cVBS transition. Here the VBS order parameters are defined based on the natural generalization of the singlet projection operator and the AFM order parameter is defined by the imbalance of the different “color” on each site.[57] We use the same definitions of the Binder cumulants as in Eq. (4a). The cumulants Uc and Us will approach 1 if there is cVBS and sVBS long-range order, respectively. If there is no such order the values will not go to 0, however, for the same reasons as discussed in Subsection 3.4. In the case of AFM order, the definition in Eq. (4a) does not account properly for the SU(3) symmetry and Uz will approach a value different from 1. In a non-AFM state the value should still approach 0. The results shown in Fig. 11 demonstrate a strongly first-order, direct transition between the two VBS states. The AFM order parameter is small and vanishes upon increasing the system size, and the value of Uz stays very close to 0.
We can conclude that the AFM order is always suppressed in the SU(3) Q3C–Q3S model and there is a direct, first-order sVBS–cVBS transition similar to the case of our SU(2) model in Fig. 5 when h is large. We can then achieve a similar phase diagram with an AFM phase and a triple point by adding Heisenberg exchange J to the SU(3) Hamiltonian. As mentioned above, for  the generalized Heisenberg model is always cVBS ordered, and previously a second-neighbor ferromagnetic Heisenberg term (i.e., on the diagonals of the
the generalized Heisenberg model is always cVBS ordered, and previously a second-neighbor ferromagnetic Heisenberg term (i.e., on the diagonals of the 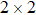 plaquettes on the square lattice) was added in order to enhance the AFM order and realize an AFM–cVBS transition for any
plaquettes on the square lattice) was added in order to enhance the AFM order and realize an AFM–cVBS transition for any 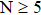 (and for any
(and for any 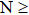 2 if a Q term is also used).[57] In our model studied here, the Q3S interactions compete against cVBS order and therefore the SU(N) J–Q3C–Q3S model should have a phase diagram similar to Fig. 5 (with h replaced by
2 if a Q term is also used).[57] In our model studied here, the Q3S interactions compete against cVBS order and therefore the SU(N) J–Q3C–Q3S model should have a phase diagram similar to Fig. 5 (with h replaced by  ). Most likely, we should also then be able to tune the AFM–cVBS from a continuous DQC transition to a first-order transition for any N.
). Most likely, we should also then be able to tune the AFM–cVBS from a continuous DQC transition to a first-order transition for any N.
5. Summary and discussionIn this paper we have proposed a sign-free designer quantum spin model, Eq. (2), that enables large-scale QMC studies of competing VBS states and different types of AFM–VBS transitions. In this section, we first summarize our main results and conclusions in Subsection 5.1, and then, in Subsection 5.2, inspired by the proposal in Ref. [41] and related arguments in Ref. [40], we further discuss possible fracton properties of the spinons in the sVBS phase. Finally, we discuss some future prospects in Subsection 5.3.
5.1. ConclusionsOur QMC results show that the  model has a ground state phase diagram with several interesting features. While the
model has a ground state phase diagram with several interesting features. While the  interactions compete, inducing columnar and staggered VBS correlations, respectively, the
interactions compete, inducing columnar and staggered VBS correlations, respectively, the  term is favorable to both kinds of orders but suppresses AFM ordering. The AFM phase separating the cVBS and sVBS phases when
term is favorable to both kinds of orders but suppresses AFM ordering. The AFM phase separating the cVBS and sVBS phases when  is absent or small therefore shrinks as
is absent or small therefore shrinks as  is increased, and eventually the model undergoes a direct phase transition between the cVBS and sVBS phases. The sVBS–cVBS and sVBS–AFM transitions are both first-order, as expected from standard Landau arguments. In contrast, the AFM–cVBS transition appears to be a Landau-forbidden continuous one for small
is increased, and eventually the model undergoes a direct phase transition between the cVBS and sVBS phases. The sVBS–cVBS and sVBS–AFM transitions are both first-order, as expected from standard Landau arguments. In contrast, the AFM–cVBS transition appears to be a Landau-forbidden continuous one for small 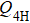 , i.e., when the sVBS phase is far away, while it becomes clearly first-order when
, i.e., when the sVBS phase is far away, while it becomes clearly first-order when 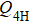 is increased and the two VBS phases approach each other. Thus, there is a triple point where the three first-order phase boundaries meet each other, and most likely there is a tricritical point on the AFM–cVBS boundary. The continuous AFM–cVBS transitions should be of the DQC type, and the existence of a tricritical point would imply that the nature of the transition can be drastically changed without changing the symmetry of the model, i.e., that symmetry-allowed terms can drive the system away from the DQC fixed point.
is increased and the two VBS phases approach each other. Thus, there is a triple point where the three first-order phase boundaries meet each other, and most likely there is a tricritical point on the AFM–cVBS boundary. The continuous AFM–cVBS transitions should be of the DQC type, and the existence of a tricritical point would imply that the nature of the transition can be drastically changed without changing the symmetry of the model, i.e., that symmetry-allowed terms can drive the system away from the DQC fixed point.
Recently, the so-called “walking” behavior in non-unitary complex CFTs[32,33] has gained attention as a way to explain the weakly first-order nature of some transitions, such as q-state Potts models with  . This scenario has also been invoked by proponents of generic weakly first-order AFM–VBS transitions.[32,34,35] Our model is the first in which the AFM–cVBS transition can be continuously tuned from what appears to be continuous to clearly first-order. This model should therefore constitute a good framework for studying the walking behavior in detail. The initial results presented here show that the emergent U(1) symmetry of the order parameter is absent when the transition becomes first-order. This behavior is in sharp contrast to the emergent higher symmetries, O(4) and SO(5), of the order parameters recently observed at some first-order AFM–VBS transitions in related models.[37,39,40]
. This scenario has also been invoked by proponents of generic weakly first-order AFM–VBS transitions.[32,34,35] Our model is the first in which the AFM–cVBS transition can be continuously tuned from what appears to be continuous to clearly first-order. This model should therefore constitute a good framework for studying the walking behavior in detail. The initial results presented here show that the emergent U(1) symmetry of the order parameter is absent when the transition becomes first-order. This behavior is in sharp contrast to the emergent higher symmetries, O(4) and SO(5), of the order parameters recently observed at some first-order AFM–VBS transitions in related models.[37,39,40]
We also discussed a generalized model with SU(n) symmetry and showed some results for the SU(3) case. It is well known that the AFM order is suppressed when n is increased,[6,7,55] and in the SU(3)  model the AFM phase existing in the SU(2) case is already absent. The AFM order can be brought back by including a Heisenberg (J) term (possibly with longer-range interactions for larger N[57]). Thus, we can in principle study phase diagrams and investigate the evolution of different phase transitions similar to what we did here for the SU(2) model.
model the AFM phase existing in the SU(2) case is already absent. The AFM order can be brought back by including a Heisenberg (J) term (possibly with longer-range interactions for larger N[57]). Thus, we can in principle study phase diagrams and investigate the evolution of different phase transitions similar to what we did here for the SU(2) model.
5.2. FractonsRecently, there have been discussions on the mobility properties of spinons in a 2D VBS state different from the ones considered here — the pVBS phase. Within a scenario in which the plaquette singlets are treated as rigid objects, spinons as well as their bound “triplon” states are fractons, restricted to motion in one dimension.[41] One prediction following from this picture is that spinons do not deconfine, and instead of a DQC transition (which in the DQC theory can take place in a cVBS or a pVBS) a first-order transition results from nucleation of triplons. However, the fracton argument for pVBS should only apply in extreme cases, as in generic quantum spin models the four-spin singlets can not be regarded as rigid objects but must be allowed to decay into dimer singlets.[40] Here we note that some of the prerequisites for fractons outlined in Ref. [41] in the context of the pVBS have analogies in the sVBS, and the latter may be a more likely host of fractons under realistic conditions. Though we do not have quantitative results from QMC simulations, we will here argue that fracton-like excitations are generically possible in sVBS states.
The fully mobile spinons play a crucial role as vortices in the DQC theory, and it is therefore interesting to compare the nature and mobility of the spinons in cVBS and sVBS states. While the two VBS phases are both four-fold degenerate, they correspond to different kinds of symmetry breaking of the lattice, thus having different minima in the Landau free energy space. The two VBS phases also host different types of domain walls, leading to different behaviors of the vortex excitations (Fig. 2). It has been explained before that the geometric structure of the cVBS pattern forces the vortex to always have a spinon in its core, and this is a crucial aspect of the continuous cVBS–AFM transition of the DQC type.[10] In contrast, the sVBS phase does not necessarily require spinons-type vortices, though vortices with spinons are also possible (Fig. 2). In the latter case, which to our knowledge has not been previously considered in this context, these spinons may be regarded as fractons, similar to the spinons recently discussed in the pVBS phase.[41]
Figure 12 shows some possible triplon excitations in the sVBS phase. Figure 12(a) shows a single valence bond in the sVBS phase being broken, creating a gapped triplon excitation. By applying J-terms in the Hamiltonian, we can see that the individual spinons can move around in two different directions; along the 45° diagonal in Fig. 12(b), or vertically along the direction of the original sVBS dimers in Fig. 12(c). In Fig. 12(d) we show how the spinons can move around by combinations of those two different moves. However, such combinations of moves in different lattice directions result in multiple domain walls depicted as gray lines in Fig. 12(d). There are two different kinds of possible domain walls,  -domain walls where a vertical sVBS pattern is adjacent to a horizontal sVBS pattern (corresponding to
-domain walls where a vertical sVBS pattern is adjacent to a horizontal sVBS pattern (corresponding to 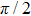 rotation in the order parameter space, or π-domain walls otherwise. In the diagrams, we indicate the
rotation in the order parameter space, or π-domain walls otherwise. In the diagrams, we indicate the 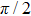 -domain walls with gray lines, and two such lines amount to a π-domain wall.
-domain walls with gray lines, and two such lines amount to a π-domain wall.
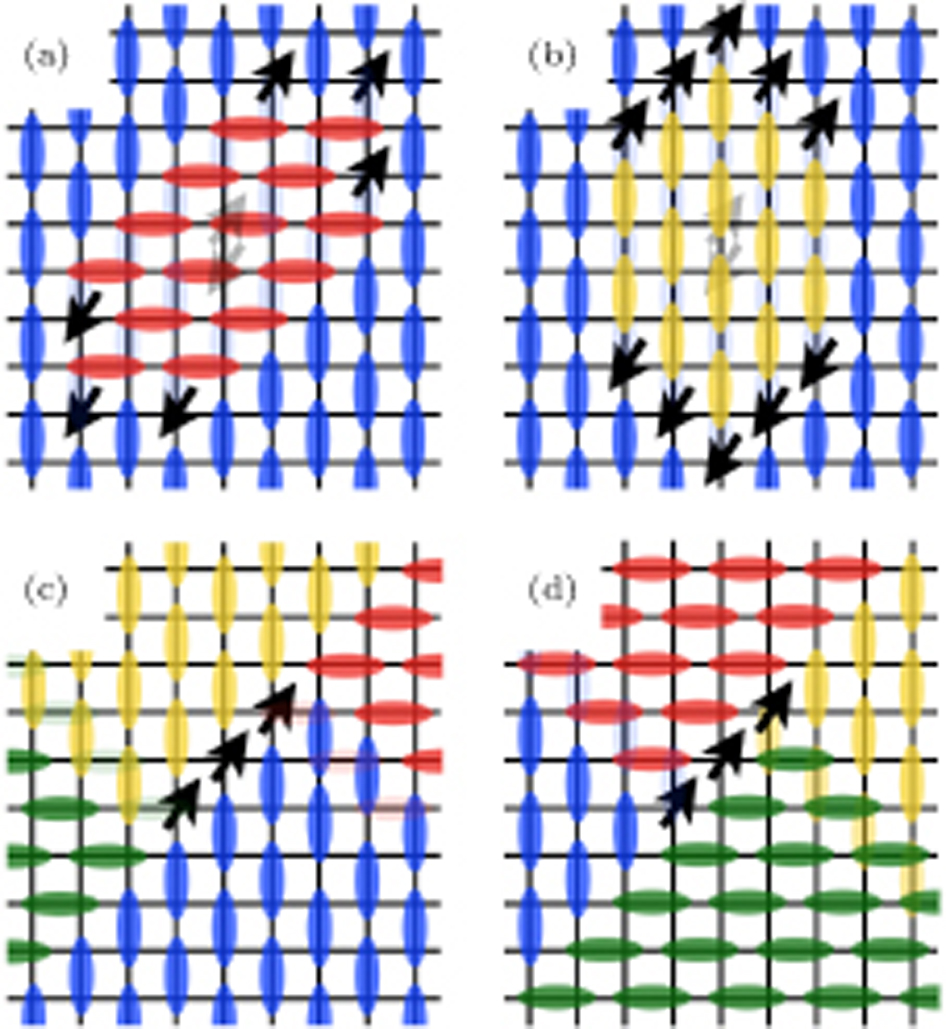
At an AFM–cVBS DQC point, it is predicted[9] and numerically observed[49] that the domain wall energy vanishes, resulting in configurations such as those depicted in Fig. 13 to contribute substantially to the low-lying excited states. The spinons can then move around essentially freely when the cVBS order weakens, hence the DQC phenomenon. In the case of the sVBS, we can see in Fig. 12(d) that there would be two different types of domain walls, which must in general have different domain wall energies. Therefore, only either (b)π/2- or (c)π-domain walls would contribute to the low-lying state, and configurations like (d) would be suppressed because of the presence also of the non-favored type of domain walls (and which one has a lower energy should depend on the specific microscopic interactions). As a consequence, the spinons are only able to move freely in one or two directions, depending on the favored domain wall type, becoming effectively fractons.
The fracton property is emergent, and in principle, the spinons can still move around in different directions in the case where the π/2-domain wall in Fig. 12(b) is preferred. For example, the spinons can not only move apart, but also come back together at a location which is not necessarily the original location where the excitation was originally created. Subsequently, the spinons can move in the other diagonal direction, and again result in a different position as a pair triplon. Overall, the triplon can move around in all directions, but the most dominant mobility of the individual spinons should be mainly restricted to the one-dimensional sublattice, and this constraint must suppress the emergent U(1) symmetry and have an effect on the nature of the phase transition. As argued in Ref. [41] in the case of the pVBS, one can expect a first-order transition due to the nucleation of spinons. The details of the nucleation process should be different in an sVBS state, as we discuss next.
The mobility properties of the spinons in the sVBS phase we have discussed now are in sharp contrast with those in the cVBS phase. As we show in Fig. 13, in the well understood cVBS phase the resulting configuration can easily fluctuate locally by applying the J-terms This mechanism only requires π/2-domain walls, which are indeed the one that is favored energetically. We can also see from Fig. 13 that the local fluctuation also allows the domain walls to thicken in the cVBS phase, thus creating alternating domains with finite area. This again contrasts with sVBS, because, as we show in Figs. 14(a) and 14(b), thickening domain walls into extended domains will necessarily require the creation of more spinons. The staggered pattern in the phase also allows the vortices to be occupied by multiple spinons, as shown in Figs. 14(a) and 14(d), which again is in sharp contrast to the cVBS case. Although in the general case it is likely that spinless vortices would be energetically favored,[45] this property of allowing multiple spinons may play a role for the first-order transitions taking place, since it allows nucleation of AFM order from clusters of spinons.
The true lowest triplon excitation state should be a superposition of the type of extended triplet valence-bond basis states discussed above, each of them transforming to a different constituent of the state when a Heisenberg J-term is applied. The specific model discussed in the preceding sections does not have any explicit J terms (two-spin singlet projector) but the same fluctuation effect is also achieved by appropriately applying the q terms Valence-bond configurations with higher diagonal energy should have a smaller contribution to the lowest triplon excitation, and by analyzing those configurations we can argue how the spinons proliferate in space. Though we have not discussed the mechanisms in a rigorous manner here, the picture is intuitive and should capture the correct physics qualitatively.
5.3. Future prospectsThe work we presented here illustrates the power of the designer Hamiltonian approach in engineering sign-free Hamiltonians exhibiting interesting phase transitions and enabling unbiased numerical studies of physically interesting situations. Our results suggest several possible follow-up studies, some of which we summarize here.
First, precisely determining the tricritical point in Fig. 5 where the cVBS–AFM transition changes from continuous to first order is an important task. If the emergent U(1) symmetry also disappears at the multicritical point, this would indicate a compelling correspondence between the emergent U(1) and continuous DQC transitions. Also, calculating the critical exponent along the critical line and comparing it with existing results for the conventional J–Q model[23] would be helpful to confirm the universality class of the DQC point. Here we should again note that the continuous transition in the conventional J–Q model has not been demonstrated completely conclusively, though there are no explicit signs of first-order discontinuities. Detailed studies of the putative tricritical point, or, alternatively, demonstrating its absence (i.e., a weakly first-order transition below the blue circle indicating the putative tricritical point in Fig. 5) would also be very useful in this regard.
We have discussed the fluctuation patterns of the order parameter inside the VBS phases. The change in fluctuation paths where the transition changes to first order can be seen as a numerical confirmation of the graph-theoretic approach introduced in the context of the AFM–pVBS transitions in Ref. [40]. Further studying when and how the fluctuation pattern between degenerate ground states changes within a single phase could shed light on what kind of phases are allowed to exist adjacent to each other in the phase diagram, and indicate relevant and irrelevant perturbations of the DQC point.
Another interesting aspect of the sVBS phase deserving further study is the nature of the spinons and their bound states. As we show in Fig. 14, the vortices in the sVBS phase can host one or several spinons, as well as no spinon. It would be very interesting to test in numerical simulations whether the multi-spinon configurations actually appear in the vicinity of the cVBS–sVBS or AFM–sVBS phase transitions, and to investigate how well the fracton picture explains the behaviors we have observed here. It should already be clear from the arguments regarding the triplon excitations shown in Fig 12 that the spinon mobility is very anisotropic, and studying dynamical aspects of the sVBS phase near criticality, e.g., the dynamic spin and dimer structure factors (using methods discussed in Refs. [59,60]) should shed further light on the nature of the excitations.