† Corresponding author. E-mail:
The work at SUSTech was supported by the National Natural Science Foundation of China (Grant No. 11974157). Part of this work was also supported by the National Natural Science Foundation of China (Grant No. 11875265), the Scientific Instrument Developing Project of the Chinese Academy of Sciences (3He-based neutron polarization devices), and the Institute of High Energy Physics, the Chinese Academy of Sciences. Kan X C and Tian M L were supported by the National Natural Science Foundation of China (Grant No. 51802002).
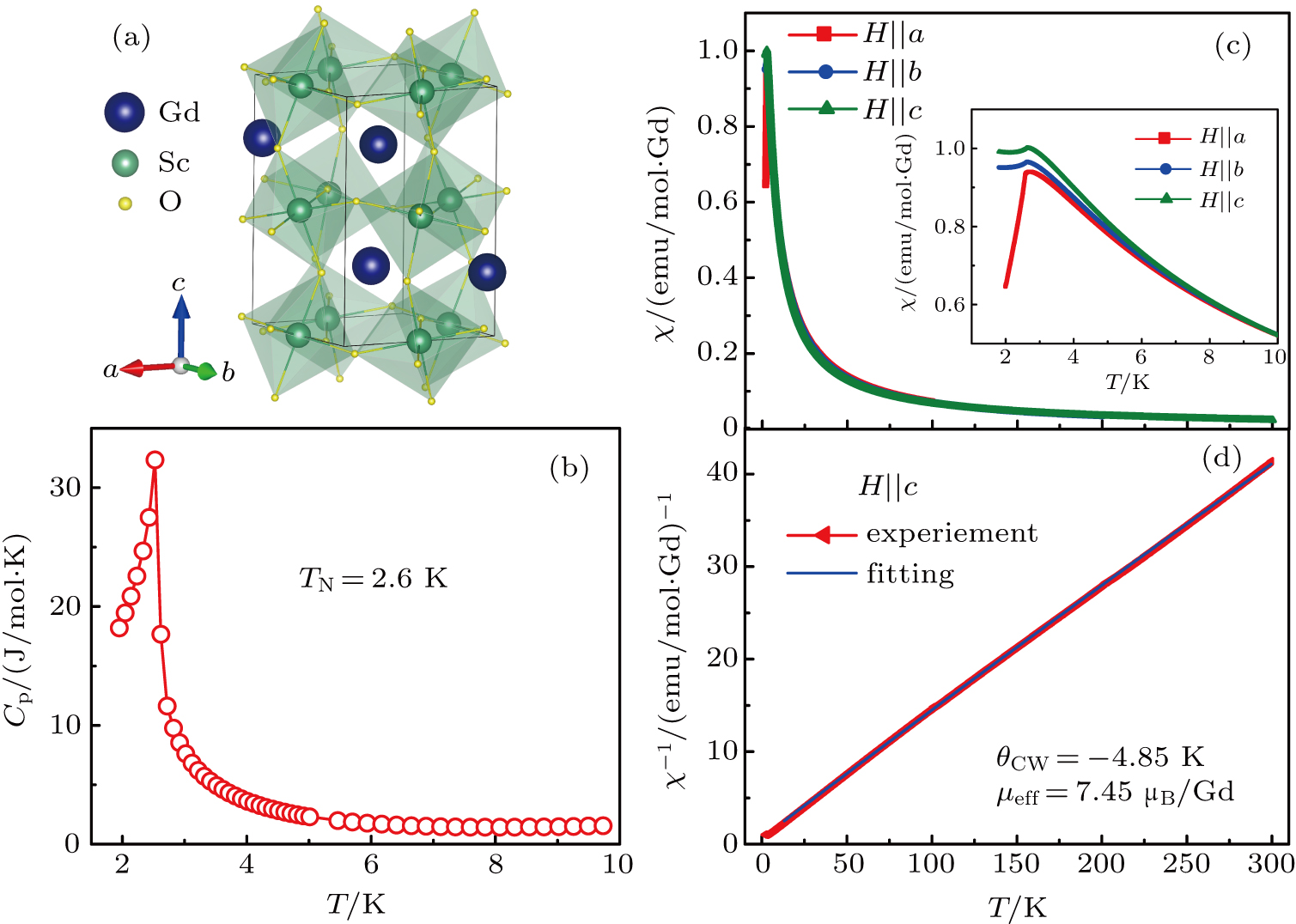
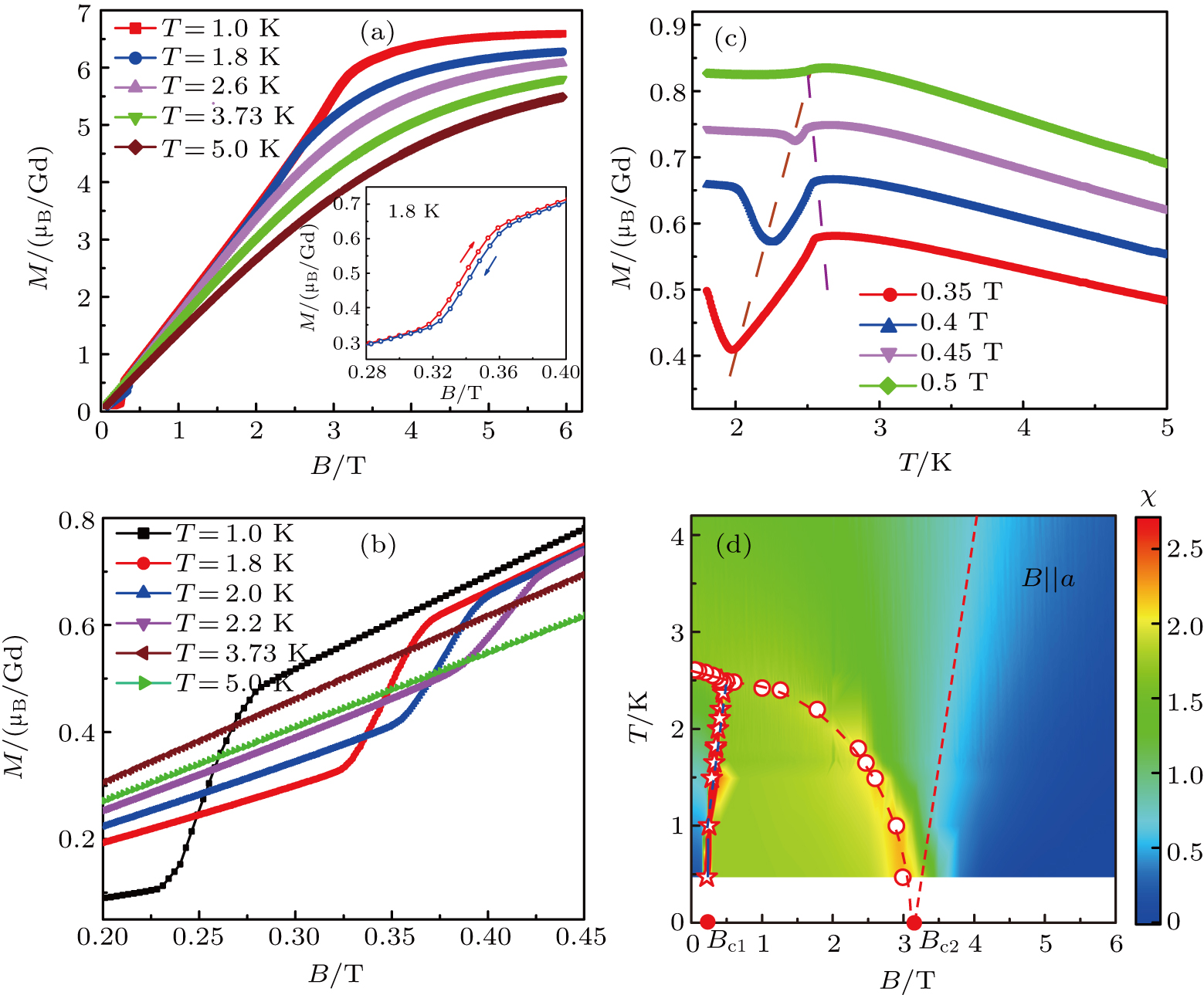
The magnetic phase diagram of rare-earth perovskite compound, GdScO3, has been investigated by magnetization and heat capacity. The system undergoes an antiferromagnetic phase transition at TN = 2.6 K, with an easy axis of magnetization along the a axis. The magnetization measurements show that it exists a spin-flop transition around 0.3 T for the applied field along the a axis. The critical magnetic field for the antiferromagnetic-to-paramagnetic transition is near 3.2 T when temperature approaches zero. By scaling susceptibilities, we presume this point (B = 3.2 T, T = 0 K) might be a field-induced quantum critical point and the magnetic critical fluctuations can even be felt above TN.
The family of rare-earth perovskite scandates RScO3 (R = rare earth) have attracted continued attention due to great variety of physical properties and potential applications. For example, the Ising-like antiferromagnet,[1] the giant magnetocaloric effect,[2,3] and the promising candidate materials for the replacement of SiO2 in silicon MOSFETs because of the large optical band gaps, high dielectric constants, andq chemical stabilities.[4–9] In addition, the RScO3 compounds with different lattice parameters have also been exploited to serve as substrates for engineering of highly strained ferroelectric and multiferroic thin films. The biaxial strain due to lattice mismatch between substrates and thin films can dramatically alter the properties of epitaxial films.[10] For instance, the SrTiO3 thin film exhibits a strain-induced ferroelectricity at room temperature when it is grown on DyScO3 substrate, compared with the paraelectric behavior of bulk unstrained SrTiO3.[11] The compressively strained BaTiO3 thin films grown on DyScO3 and GdScO3 substrates can also produce larger ferroelectric (FE) polarization and higher FE transition temperature.[12]
Apart from the effect of strain, the intrinsic properties of RScO3 substrates may also play important effect on the properties of thin films. For example, the magnetic properties of RScO3 should be took into account when they are used as substrates for magnetic oxide thin films.[13] However, due to the low magnetic ordering temperatures of RScO3, normally only a few Kelvin degrees,[13–15] the magnetic effects from the substrates to the magnetic thin films are usually neglected and have not been the subject of detailed investigation. However, some of this series compounds still exist strong magnetic correlation well above the magnetic transition temperature, which cannot be ignored even at dozens of Kelvin degrees, such as the short range magnetic order discovered in DyScO3 at 30 K.[1] Actually, it was argued that these strong fluctuations are enhanced by the one dimensionality of the rare earth magnetic spin chains. Indeed, the quantum critical Tomonaga–Luttinger liquid behavior has been reported in YbAlO3,[16] and the strong orbital couplings and crystal field effects was claimed to be crucial for the unexpected low dimensionality behaviors.[1,16,17]
On the other side, for GdScO3, with the electron configuration of Gd3+ is 4f7 and L = 0, no spin–orbit coupling is expected. Thus following the arguments in previous studies,[1,16,17] the low-temperature magnetism of GdScO3 should behave very different, comparing with DyScO3 and YbAlO3. Despite that GdScO3 has been reported as a giant magnetocaloric system with an antiferromagnetic (AFM) transition, TN = 2.6 K,[3] the details of the magnetic phase diagram and Gd–Gd interactions still remained poorly understood. Moreover, the studying of the Gd–Gd interactions in GdScO3 may also be very helpful to understand the complex magnetism in GdFeO3 and GdMnO3.[18,19]
High-quality single crystals of GdScO3 used here are commercially available.[12,20] Magnetization measurements were performed using two magnetometers for different temperature ranges: (i) commercial vibration sample magnetometer Quantum Design Magnetic Property Measurement System (MPMS-VSM) for the high-temperature measurements T = 1.8 K–300 K; (ii) MPMS-3 with 3He insert for the temperatures T = 0.5 K–1.5 K. Heat capacity measurements were performed on the Physical Property Measurement System (PPMS) in the temperature range 1.8 K–300 K.
As shown in Fig. 
Figure
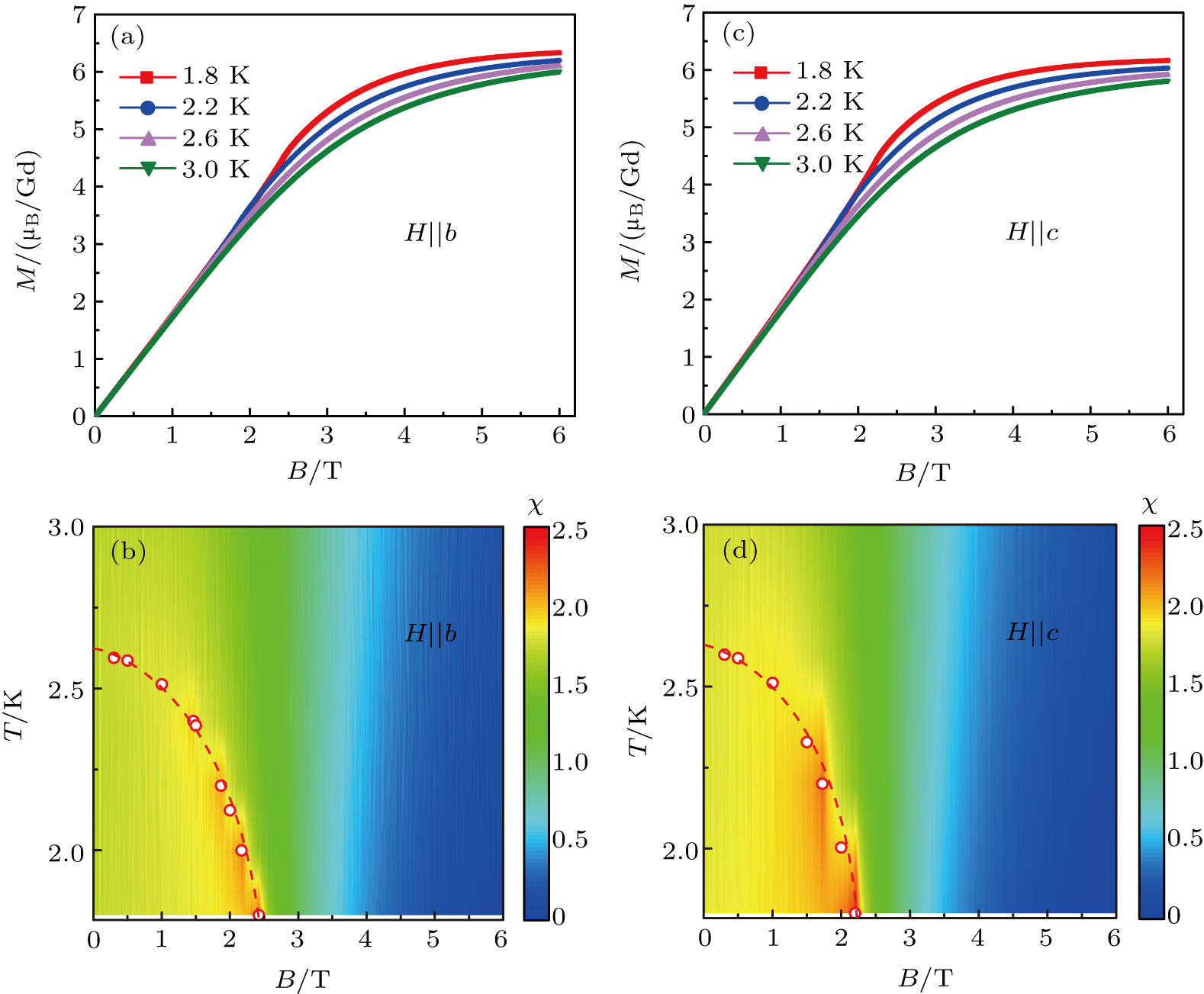
The measurement of isothermal magnetizations of GdScO3 with applied field along the b and c axes from 1.8 K to 3.0 K is shown in Figs.
It usually believed that the AFM phase will directly enter into trivial PM phase in GdScO3 with the applied field increased. However, since the AFM–PM transition is of second order and the transition temperature is gradually suppressed by the applied field, it might be existed a quantum critical field Bc2 at 0 K, where the AFM state transforms into the PM state. Around the QCP, the magnetic fluctuations are quantum mechanical in nature, which can exhibit scale invariance in both space and time. Unlike classical critical points, where the critical fluctuations are limited to a narrow region around the phase transition, the influence of the QCP can be felt over a wide range of temperatures above the QCP, so the effect of quantum criticality is felt without ever reaching 0 K. Figure
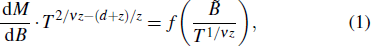
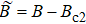

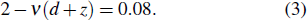

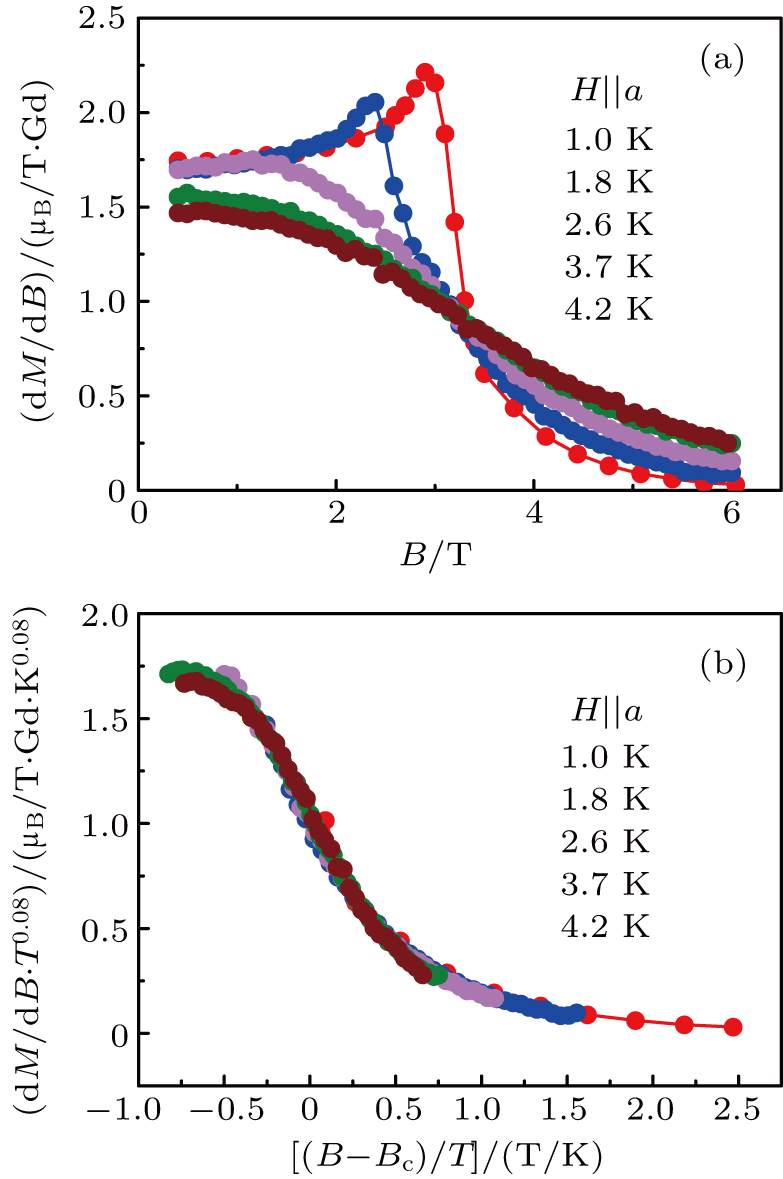 | Fig. 4. (a) Field dependencies of the magnetic susceptibility χ = d M/d B from 1.0 K to 4.2 K with field along a axis. (b) Critical scaling of the magnetic susceptibility in panel(a). |
As previous discussed, in GdScO3, the orbital contribution (L = 0) is absent, and the magnetic ground states of Gd3+ are isotropic eight-degenerated S = 7/2 states. Due to the large spin values of S = 7/2, the in plane exchange interactions of the form JS ⋅ S are greatly enhanced, and become dominant in GdScO3 and GdAlO3.[23]
On the other hand, although sharing the same crystal structure, the situations in YbAlO3 and DyScO3 are completely different. Due to the large orbital contributions, the degenerated spin states of YbAlO3 and DyScO3 are lifted by the crystal field effect, and the ground states are well separated Kramer doublets. These doublet ground states could be treated as effective spin S = 1/2, which turns out to be crucial for observed unconventional one dimensional physics in YbAlO3 and DyScO3 and related systems.[16,17]
In summary, we investigated the magnetism and heat capacity of single crystal GdScO3 at low temperatures. GdScO3 is an uniaxial antiferromagnet with the easy axis of magnetization along the a axis. The Néel temperature is found to be 2.6 K. The magnetization measurements show it exists an SF phase transition when the applied field along the a axis. The field-temperature phase diagrams for B along the three principle crystal axes are established. By scaling the magnetic susceptibilities, we demonstrate there might be a quantum critical point (QCP) at B = 3.2 T and T = 0 K corresponding to the AFM-to-PM phase transition. Compared to the one-dimensional physics observed in YbAlO3 and DyScO3, the magnetic structure and the critical scaling indicate that the in-plane exchange interactions are more important in GdScO3. It is found that quantum critical like fluctuations affect the physical properties over a large temperature and field area in GdScO3, and additional caution may need be paid at low temperatures, when it was treated as a simple PM substrates for the epitaxial growth of magnetic thin films.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |